不同采集设备时间对准研究及误差分析*

夏 栋，王守权，王艳军

（海军航空大学青岛校区，山东 青岛 266041）

0 引言

在数据采集和测试领域，经常出现需要对不同采集设备记录的参数数据进行对比分析的情况。不同采集设备只有记录了时戳（即时间标记或时间信息），对同一时刻不同设备中参数数值的对比分析才会有意义［1］。时间信息一般通过GPS 或北斗导航系统获得［2］，但是多数采集器并没有配备导航系统［3-5］，或者仅仅配设本地时钟。在上述情况下采集器记录数据就缺少绝对时间信息。如果不采取措施解决时间对准问题，数值对比分析的结果将会出现错误。因此，如何实现时刻统一（即时间对准）是不同采集器记录数据对比分析的一个非常重要且必须解决的问题。实际上在数据采集过程中经常会出现多个采集设备都采集了同一个参数，比如在航空领域起落架收起既记录在了飞参数据中，也记录在了火控任务数据中。对于不同采集器中同一个参数的记录数据，随时间状态变化过程理论上应该是相同的。本文将研究采集设备没有时间信息的情况下，通过不同采集设备都记录的关键参数的关键变化节点实现时间对准的方法。

1 不同采集设备基于关键参数的时间对准

用于时间对准的关键参数优先选择离散量和开关量，我们以开关量为例。如果一个开关量同时被两个采集器采集，在不考虑采集时间误差的情况下，该开关量在两个采集器中状态发生相同变化的时刻，理论上是一致的。基于该理论，只要在该时刻对两个采集器的采集时间进行对准，并且两个采集设备的采集频率已知，那么两个采集器任意一个采集点都可以通过计算时间差来实现对准。下面先研究采集设备工作起始时间的对准。

设第1 个采集器的采集起始时刻为Td1_0，采集频率为f1，第2 个采集器的起始时刻为Td2_0，采集频率为f2。对于同一采集参数，设采集器1 中参数状态变化发生在第m 个采集数据，采集器2 中参数同样的状态变化发生在第n 个采集数据。为了实现时间对准，两个采集设备需要统一的计零时刻，一般取两个采集器起始时刻的最小值，若Td1_0＜Td2_0，设计零时刻T0=Td1_0。由图1 参数状态变化采集时刻t 可用两采集设备的记录时刻分别表示为：

由上式可以得到采集设备2 的采集起始时刻。

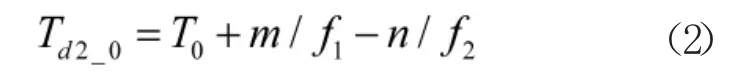
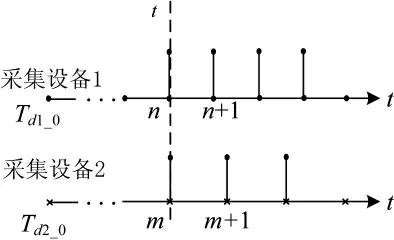
图1 两个采集设备的时间对应关系

进而可进一步得到采集设备1 和采集设备2在任意一个采集点的采集时刻。采集设备1 第i 个采集点的发生时刻为：

采集设备2 第k 个采集点的发生时刻为：

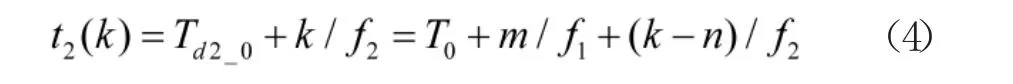
2 特定时刻参数插值计算

如图1 所示，由于不同采集设备的采集频率一般情况下不同，两个采集设备不同采集点发生的时刻是相互错开的。当选定的对比时刻处于两个采集点之间时，为提高精度参数值需要通过内插得到［6］。

以采集设备1 为例，设需要t 时刻的参数值。由式（5）可得到，t 时刻前一个采集点n 的采集时刻为t1（n），对应的参数值为zn；t 时刻后一个采集点n+1的采集时刻为t1（n+1），对应的参数值为zn+1。由于t1（n）到t1（n+1）之间的时间间隔很短，可以认为在这段时间内测量值是线性变化的，通过对zn和zn+1进行线性插值，就可以得到采集设备1 在t 时刻记录的参数测量值z（t）。具体的插值公式为：

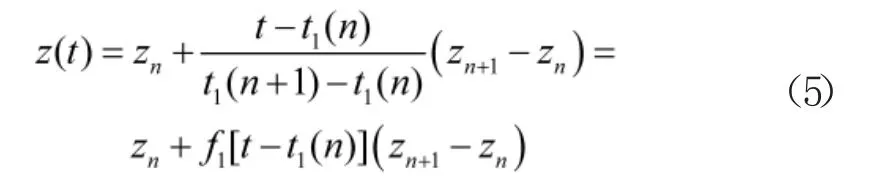
利用同样的方法，也可以得到采集设备2 在任意时刻的值。

3 时间对准误差分析

由于采集器等时间间隔取值，参数状态发生变化可能出现相邻采集时刻的任意位置，因此，上述对准方法是存在时间对准误差的，下面将分析对准误差的大小。

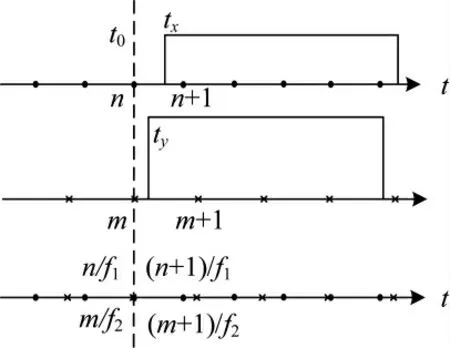
图2 参数采集时间示意图

为了得到采集时间误差z 的概率分布特性，先来计算z 的概率密度函数。由于x 与y 相互独立，因此，z=y-x 其实是两个独立变量差的概率密度函数求解。下面先计算z 的概率分布函数，求导后可得到概率密度函数［7-8］。设两个独立变量x 与y 的概率密度函数分别为p1（x）和p2（x），两者的表达式如式（6）和式（7）。

那么z=y-x 的概率分布函数应该是x 与y 联合概率密度函数在图中阴影部分的积分［9］，如式（8）所示。

图3 独立变量差值概率分布积分区域

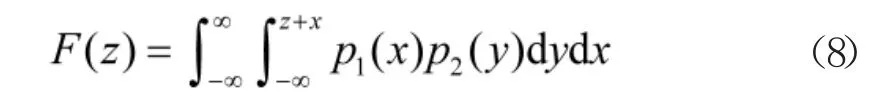
引入一个中间变量v，令v=y-x，则上式可表示为：

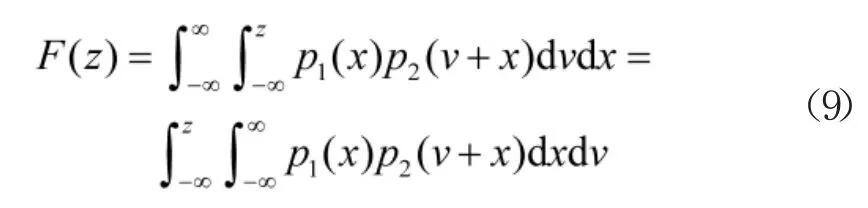
对F（z）求导得到z 的概率密度函数p（z），如下式所示。

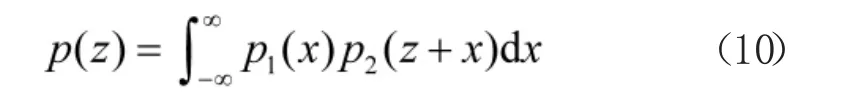
再由p1（x）和p2（y）的表达式（6）和式（7）可以得到，当f1≥f2时，

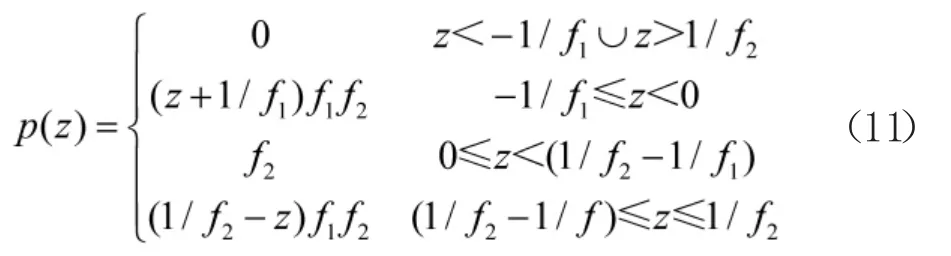
因此，当f1＜f2时，p（z）的表达式为：

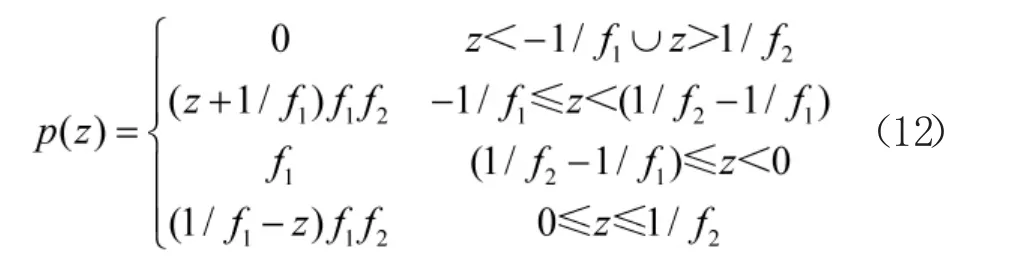
两种情况下的概率密度函数曲线如图4 所示。

图4 z 的概率密度函数

根据概率密度函数p（z），z 的均值为：

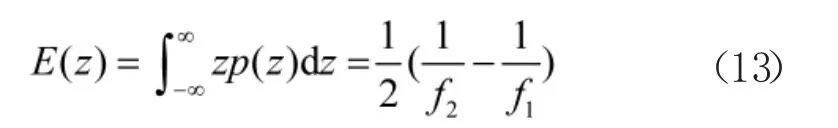
z 的方差为：

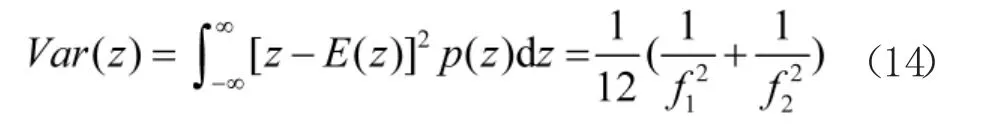
由z 的方差求解结果可以看出，采用关键参数对两个记录设备的采集时间进行对准时，对准误差跟两个采集设备的采集频率有关。两采集设备的采集频率越高，时间对准的误差越小。在实际工作过程中往往会出现一个采集设备的频率远高于另一个，由式（14）可以看出时间对准误差取决于较低的采集频率。

下面对一例具体的两采集设备时间对准问题进行分析。假设某型飞机飞参采集器采集频率为f1=10 H z，而加装的雷达数据记录仪的采集频率为f2=50 H z。两个采集设备都采集了“起落架收起”信号，落下为0、收起为1。雷达记录仪没有记录飞机平台的经纬度和高度位置，当对雷达距离和角度测量精度进行评估时，需要通过飞机平台的经纬度和高度信息计算被探测目标的真实距离和角度，就需要利用飞参系统记录的飞机平台经纬度和高度信息。两个采集器均为时间向下取值，在该情景中时间对准误差的范围为［-0.1 s，0.02 s］。由式（13）得，时间对准误差的均值为-0.08 s，该值可通过修正将偏差补偿掉。由式（14）得，时间对准的方差为0.000 87 s2。由方差取值可以看出时间对准的精度较高，并且如果较低频率采集器的采集频率变高，对准精度会进一步提高。

4 结论

在数据采集和分析领域，经常出现需要对不同采集设备记录的参数数据进行对比分析，而统一的时间基准是分析结果正确的前提。当采集设备没有时间信息时，可通过不同采集设备对同一个关键参数发生相同的状态跃变的时刻进行时间对准，并通过插值计算得到任意时刻的值。经过理论分析，该方法可以实现较高的时间对准精度。对准误差与两个采集设备的采集频率有关，采集频率越高，对准误差越小。当两个采集设备采集频率相差较多时，对准误差由低频率的采集设备确定。