光伏电站短期功率区间预测

赵 辉，赵智立，王红君，岳有军

(1.天津理工大学电气电子工程学院，天津 300384；2.天津农学院工程技术学院，天津 300392)

光伏发电技术是近年来发展迅速的新能源技术，具有光明的发展前景。据统计，2019 年全球新增光伏发电装机容量110 GW，累计装机达到616 GW，比2018 年增长了7.91%。随着国家太阳能发电示范项目的大力推进，截止2019 年底，我国新增的装机容量占到全球的40.9%，其中已经并网运行的光伏电站9 座，总的装机容量219 GW[1]。

目前，光伏系统产生的电能受天气变化影响较大，导致光伏出力具有较强的波动性和不确定性，为了更好地描述光伏出力的不确定性，提出光伏出力区间预测方法。王等[2]提出改进深度受限玻尔兹曼机算法的光伏发电短期功率概率预测，在一定置信水平下，实现了较好的区间预测，该方法的不足是无法避免假设实验与计算复杂的弊端。黎等[3]通过粒子群算法-边界估值理论(PSO-LUBE)建模对光伏出力进行区间预测，用PSO 优化LUBE 输出权重，直接一步给出最优区间，在三种置信度下表现出较好效果，但是未考虑原始功率序列的内在特性。余等[4]提出基于变分模态分解-样本熵-最小二乘支持向量机(VMD-SE-LSSVM)的光伏出力短期预测方法，实验表明，分解后的功率子序列具有更好的非线性拟合能力，但由于光伏发电预测结果受各种环境变量影响较大，单纯依靠功率时间数据特性来预测很难达到理想精度。

综上，本文采用气象因素结合功率序列共同构建预测模型来提高预测精度。利用自适应噪声的集合经验模态分解(CEEMDAN)对原始功率序列进行分解，降低非平稳性；采用核极限学习机(KELM)双输出结构直接作为光伏出力预测的上下限，将区间评价指标作为约束条件来调整预测区间，避免了传统区间预测的繁杂计算和假设实验；使用改进的蚁狮算法(IALO)算法对KELM 的输出层权重进行动态调整，提高了区间预测可靠性。

1 预测原理分析

1.1 数据处理方法

CEEMDAN 是对EEMD 的改进，可以有效地处理非线性和非平稳性的数据序列。为了提高运行效率和减小模态混叠，CEEMDAN 在分解原始序列S(t)中添加满足正态分布的高斯白噪声ei(t)，则第i次的信号可以表示为Si(t)=S(t)+εei(t)(i=1,…,I)。首先，EEMD 对历史功率信号Si(t)重复分解I次，获得首个模态分量以及余量；然后，在余量中添加高斯白噪声，再分解得到下一个模态分量和余量；最后重复上述过程，直到不能分解[5]。排列熵(PE)表示了时序规则程度的大小，可以量化各分量的复杂程度，时间序列越规则，则排列熵值越小；反之，越大。相近的PE值序列合并为新序列，提高计算效率，为后面的各分量模型的建立提供理论基础[6]。

1.2 改进的蚁狮算法

蚁狮优化算法(ALO)是Mirjalili[7]在2015 年根据蚁狮与蚂蚁之间捕食关系而提出的一种新颖的群智能优化算法，具有调参量少和收敛精度高的优点。但随着迭代次数的增加也存在过早收敛、局部最优等问题。为了解决上述问题，提出一种自适应的边界非线性递减策略，来解决同一轮迭代中蚂蚁边界游走不变性而导致的算法多样性不足的问题；引入位置更新动态权重系数，来合理分配蚂蚁选择蚁狮和精英蚁狮的概率，更大程度上避免局部最优[8]。IALO 步骤有5 步。

步骤(1)：随机初始化蚂蚁和蚁狮群体的位置，根据适应度值大小选取最优个体作为精英蚁狮，设定最大迭代次数为tmax，蚂蚁和蚁狮种群大小均为N。

步骤(2)：蚂蚁在搜索空间内随机游走，位置更新定义为：

式中：cumsum是累加和；t为随机游走的步长(文中指迭代次数)。

步骤(3)：蚁狮布置陷阱以及诱使蚂蚁进入陷阱，蚁狮通过调整蚂蚁随机游走边界上下限的大小来进行诱捕，定义关系式如下：

式中：i表示第i只蚂蚁；Antliontj表示第t次迭代第j个蚁狮的位置；d t、ct分别表示第t次迭代的所有蚂蚁位置移动的最大值和最小值。为了防止进入陷阱附近的蚂蚁逃脱，随着迭代次数变大，蚂蚁随机游走的边界范围逐渐缩小，定义如下[8]：

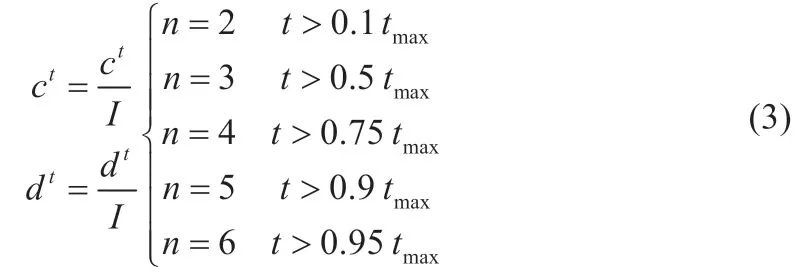
式中：I=10n(t/tmax)，其中，t和tmax分别为当前迭代次数和最大迭代次数，n为常数，由t来决定。

由I=10n(t/tmax)和式(3)可知，蚂蚁围绕蚁狮游走的边界随迭代次数增加而减小，呈现线性分段变化且在同一轮的迭代中全部蚂蚁随机游走的边界值是不变的，影响算法多样性。为了解决这个问题，对公式I=10n(t/tmax)进行改进，改进后的公式如下：

式中：rand为[0,1]内的均匀分布的随机数，增强蚂蚁游走的随机性；10n、t/tmax分别为线性分段指数递增和线性递增，0.5+cos[(2tπ/tmax)·rand]在[0.5,1.5]呈现非线性递增，则I总体上为非线性递增。由式(3)可知，I与蚂蚁游走边界变化呈负相关，所以蚂蚁随机游走的边界呈非线性递减，从而增加了蚂蚁随机游走的多样性，增强了全局搜索能力。

步骤(4)：蚂蚁滑落到陷阱底部被蚁狮捕捉，若种群中包含适应度高于蚁狮的个体，则该个体将作为新蚁狮重筑陷阱。同代选择适应度最好的蚁狮作为精英蚁狮，并且与蚁狮一同指引蚂蚁位置更新，但是经过实验证明蚂蚁大概率围着精英蚁狮随机游走，这就导致蚁狮被边缘化，不能充分进行全局探索而陷入局部最优，如下式所示：

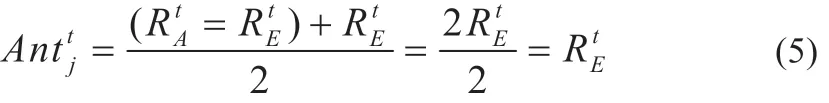
式中：RtA、RtE分别为蚂蚁围绕蚁狮和精英蚁狮随机游走的位置。为了解决上述问题，文中提出一种动态权值比例系数分配的方法来改进蚂蚁位置更新公式，平衡全局和局部寻优能力，提高算法性能。改进公式如下：

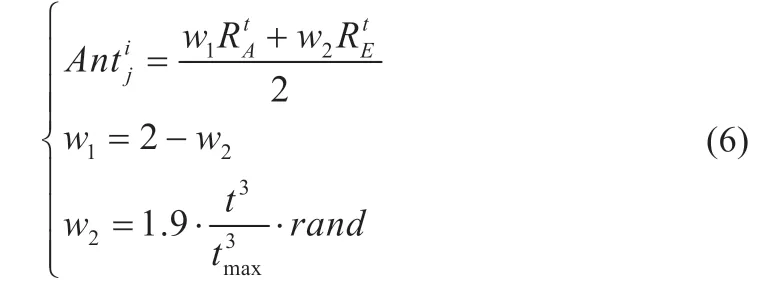
式中：w1和w2分别为权重系数，由式(6)可知w1的步长变化范围为[0.1,2]。文中为了解决蚁狮算法探索与开发的不平衡性，利用非线性递减权重系数进行改进，并且加入随机因子来提高种群多样性。前期w1较大，蚂蚁在蚁狮周围游走，可以充分发挥全局搜索能力，后期w2逐渐变大，蚂蚁在精英蚁狮周围游走，可以增强局部寻优能力，从而提高算法性能。

步骤(5)：判断是否达到最大迭代次数，是，则结束；否则，回到步骤(2)继续执行算法。

1.3 核极限学习机

极限学习机(ELM)是单隐层前馈网络，为了减少极限学习机权重随机性和网络训练时间，Huang 等在2015 年提出KELM。KELM 是将核学习和ELM 结合，以核映射代替ELM中的随机映射。本文采用了基于径向基函数(RBF)的KELM，可以将特征映射到更高维的空间，有更好的学习效果和更强的非线性映射能力[9]。

2 预测区间的构造以及评价指标

2.1 预测区间构造

利用单隐层网络KELM 来训练原始数据，调整网络的输出节点个数，对预测区间上下界直接输出，计算简单、易实现。将处理好的数据分别进行模型训练时，把实际输出功率的大小按照一定百分比扩大和缩小当作初始区间，利用IALO 算法优化预测模型获得最优的参数，从而获得最优且可靠性高的区间，并对各分量子模型的区间上下限对应相加得到最终输出区间，模型结构如图1 所示，xn为输入变量，w为输入层和隐藏层之间的连接权重，β 为输出权值，H(x)为隐含层节点的输出函数，Ui和Li分别为光伏功率预测区间的上下限。

图1 区间预测模型结构

2.2 区间评估指标

区间评价指标中预测区间覆盖率(PICP)值越大，所构造的预测区间可靠性越高，实际值覆盖率越高。定义式如下：

式中：N为样本数；θi为一个布尔值。

式中：yi为预测目标；Ui和Li分别为区间的上限和下限。在满足额定置信度的前提下，减小区间宽度才能增加预测结果的可信度。因此，引入预测区间平均宽度(FIAW)：

式中：N为训练样本数；R为预测目标的范围，用于归一化处理。所以构造预测区间的验证标准是在PICP足够大的条件下，FIAW足够小。然而，在原理上这两个指标函数是有矛盾的，覆盖率越高，区间自然会更大；相反，区间越小，覆盖率越低。为了解决这个问题，提出综合评价指标[10](CWC)：

式中：μ 表示置信水平，且μ=1－α；η 表示调整CWC大小的参数，当PICP低于μ 时，将对CWC指数式惩罚，η 范围为50～100。

2.3 IALO 优化KELM 区间预测

本文以区间评价指标为约束条件，利用IALO 算法优化KELM 的网络参数，获得最优的输出权重，从而直接生成最优预测区间。IALO 优化KELM 算法流程如图2 所示。

3 算例分析

3.1 数据预处理与分析

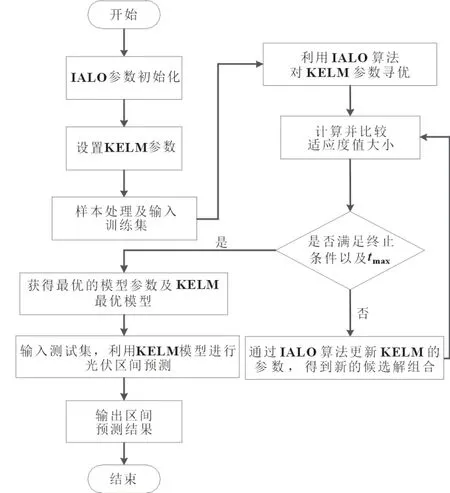
图2 IALO优化KELM算法流程

以澳洲光伏研究中心(DKASC)的太阳能发电系统为研究对象，选取2018 年7～9 月的天气和功率的时间序列作为历史数据，由于光伏出力的间歇性，所以研究每日8：00～17：00的出力情况，历史功率序列与天气数据收集间隔为1 h，共910 组数据。利用相关性分析法来确定输入数据的尺度，也就是根据功率数据自相关性的大小来确定输入变量个数。自相关系数如表1 所示，选择自相关系数ρ 大于0.9 的数据作为输入数据，前6 个数据作为输入数据，第7 个数据作为预测数据，以此类推循环预测。本文选取880 组为训练集，30 组为测试集。

表1 样本序列的自相关系数

基于CEEMDAN 算法分解原始光伏功率信号，得到9 个模态函数(IMF)分量和余量Rn，其中，噪声标准偏差为0.2，白噪声组为600，最大迭代次数为200，分解的具体结果如图3所示。

图3 CEEMDAN分解光伏功率序列

由于输入维度m对分解效果影响较大，重复实验确定m=3 和延时间隔τ=1 时序列复杂度差异明显，对分解后的每一组子序列进行熵值计算，对PE归一化后，如图4 所示，各IMF的PE值逐渐下降，则表明其非平稳性减小，分量从IMF1到Rn复杂度稳步减小，对相近PE分量合并。IMF1和IMF2的PE值相近且最大，不确定性最高，合并成新序列1；IMF3与IMF4和IMF5～IMF9呈现出较强的不确定性，PE差值都在0.1以内，可以分别合并为新序列2 和3；余量Rn较平稳，可以作为一个新序列4。

图4 各IMF分量和余项Rn

3.2 IALO-KELM 预测

利用新序列分别构建模型，并在Matlab 平台上进行仿真实验。因光伏功率受环境因素(如辐照度S，温度T，湿度H)影响较大，所以选取天气因素加入到输入变量。结合经验公式和多次实验，确定KELM 的输入层节点为6，输出层节点为2，核参数为0.2，惩罚系数为0.5，IALO 算法的种群大小为40，最大迭代次数为300。将区间评价指标作为目标函数，适应度越小，则预测精度越高，IALO 适应度迭代曲线如图5 所示。

图5 IALO适应度迭代曲线

3.3 实验结果分析

根据建立好的CEEMDAN-PE-IALO-KELM 模型进行仿真实验，区间预测结果如图6 所示。

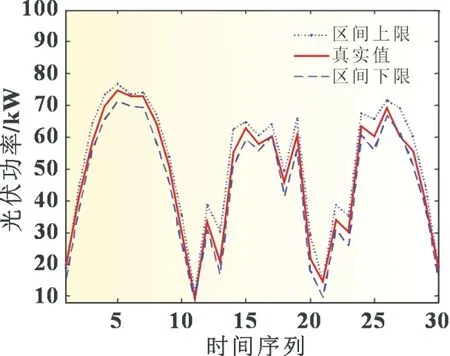
图6 90%置信度下CEEMDAN-PE-IALO-KELM 模型预测结果

为了证明所采用方案的可行性，在相同条件下，分别与IALO-KELM、粒子群算法-反向传播算法(PSO-BP)两个不同的模型预测结果对比，如图7～8 所示。

为了与其他模型进行直观地对比，表2 列出了置信度为80%、90%的区间评价指标PIPC、FIAW、CWC。由表2 可知，本文模型比IALO-KELM、PSO-BP 模型具有更高区间覆盖率和较低的区间宽度，区间综合评价指标也较小。不同的置信水平下，虽然本文模型与IALO-KELM 和PSO-BP 模型的覆盖率相近，但是后两者模型的区间宽度明显大于本文模型，说明采用分解算法和IALO 与另两种算法相比，区间预测精度有很大的提高。

图7 90%置信度下IALO-KELM预测结果

图8 90%置信度下PSO-BP预测结果

表2 各预测模型区间评价指标对比

4 结论

本文构建了基于CEEMDAN-PE-IALO-KELM 的短期光伏区间预测模型，并将预测结果与IALO-KELM 和PSO-BP 模型进行比较。在同一置信水平下，通过仿真分析对区间评价指标(PIPC、FIAW、CWC)进行数值对比，验证了所提出的CEEMDAN-PE-IALO-KELM 模型方案的可行性。

仿真结果表明，采用CEEMDAN 的分解方法可有效降低原始功率信号的非平稳性，IALO 算法优化KELM 网络能更快地进行全局寻优，避免陷入局部最优的缺点，本文所采用的方法有更好的区间预测效果。因此，所提出的CEEMDANPE-IALO-KELM 模型在电力系统的实际应用中具有一定的意义。