基于改进POT 模型的混凝土坝监控指标拟定

唐贤琪 ，杨海云，吴 凡，何金平

(1. 武汉大学 水利水电学院，湖北 武汉 430072；2. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉430072；3. 国网福建省电力有限公司电力科学研究院，福建 福州 350007)

监控指标是对大坝荷载或效应量安全界限作出的规定[1]，是判断大坝结构性态是否正常的科学依据，可以帮助管理者制定大坝安全运行和维护计划，及时发现大坝潜在的安全隐患，确保大坝始终处于安全运行状态。大坝安全监控指标拟定方法的研究已取得了较丰富的成果。李珍照[1]对采用监测数学模型拟定监控指标的方法进行了比较深入的研究；吴中如等[2]对大坝监控指标的拟定方法进行了比较系统的研究，包括拟定监控指标的小概率法，利用监测资料结合结构分析反演监控指标的方法，并对监控指标的等级划分进行了深入探索；魏德荣[3]对监控指标的内涵进行了诠释，对拟定监控指标的基本思路进行了研究；何金平等[4]对基于多测点监测模型的监控指标拟定方法进行了探讨；盛金保等[5]将风险分析应用于大坝安全监控之中，提出了基于风险的大坝预警指标和应急预案。此外，一些学者还将现代数学理论引入到大坝监控指标的拟定之中，探索了一些新思路和新方法[6-8]。大坝安全监控指标研究成果根据其所依据的基本原理可概括为三大类：一是监测模型法，该方法以各类监测数学模型对监测效应量变化规律的有效刻画为基础，能较好地描述内在和外在因素对监测效应量的影响模式和影响程度，但建模时对效应量与环境量的完整性和可靠性要求均较高；二是结构分析法，该方法依据结构破坏机理，采用相应的结构分析方法对特定工况下的效应量进行理论计算，然后将实测值与计算值进行比较和分析，其物理力学概念明确，但只适用于安全界限在规程规范上具有明确规定的情况；三是概率分析法，该方法将监测效应量视为随机变量，每测次的测值被视为一次随机试验的结果，利用统计学原理，推求某一失效概率下监测效应量的数值表现，但概率模型的参数取值等受主观性和经验性因素影响较大。上述3 种方法分别从不同的角度开展了大坝安全监控指标拟定方法的研究，为监控指标研究提供了丰富的途径。

以统计学中极值理论为基础的典型小概率法、POT 模型法等都属于拟定监控指标的概率分析法。典型小概率法在监测效应量测值全序列中选择不利荷载组合条件下的测值构成一个新的子样本序列[2]，然后根据该子样本序列的概率分布和大坝的失事概率来拟定相应的监控指标；但在实际应用中，典型小概率法一般选择年最大值或年最小值构成子样本序列，因而监测信息的利用率较低。POT 模型法先按一定的规则确定阈值，再以超阈值测值构成子样本序列，有效地保留了极端观测值，从而大大地提高了信息的利用率，目前已成功应用于工程安全监控领域预警指标的拟定中[9-11]。

在POT 模型中，阈值的确定是关键。现有的阈值确定方法主要有Hill 图法、超出量均值函数图法及样本峰度选定法等[12]。其中，Hill 图法和超出量均值函数图法均属于图形法，比较直观，但确定曲线拐点时需要人工判断，主观性较大，且难以实现计算机自动判断；样本峰度选定法概念比较清晰，但计算过程十分繁琐。因此需要对阈值的确定方法进行改进，寻找能客观且可采用计算机程序自动识别的阈值确定方法。

本文基于POT 模型的基本原理，在构建超阈值子样本序列时，以概率论中的3σ 准则为确定阈值的理论基础，提出了一种能客观、定量地确定阈值的方法，从而对传统的POT 模型进行了改进，并对改进方法的合理性进行了验证。

1 改进的POT 模型

1.1 POT 模型基本原理

式中： ξT为形状参数； σT为尺度参数。

GPD 分布的形状参数 ξT和尺度参数 σT的估计方法主要有极大似然估计法、概率权矩法和矩估计法等[14]。其中极大似然估计法理论基础较严谨，矩估计法可操作性较强。

PBdH 定理认为，无论原始测值 xi的分布函数F(x)是何种分布形式，都可将超出量 yj的分布函数近似地视为GPD 函数FT(y)，这就很好地解决了超出量分布函数的假定和检验问题。

1.2 改进的阈值确定方法

2 工程实例

某水电站枢纽工程为Ⅰ等，主要建筑物为Ⅰ级，拦河大坝为混凝土重力坝，最大坝高84 m。水库为年调节水库，正常蓄水位95 m；除汛前处于防洪限制水位运行外，其他时段库水位基本在正常蓄水位附近小幅变化。为监测该大坝安全，在坝顶布置了一条引张线，引张线编号EX4；共布置10 个测点，测点编号分别为EX401～EX410。

以该引张线上的EX406 测点为例，采用本文提出的基于3σ 准则的改进阈值确定方法，拟定该测点水平位移监控指标。样本时段为1996 年6 月1 日—2015 年6 月1 日，样本总数n 为236 个；规定水平位移向下游方向为正，向上游方向为负。图1 为EX406 测点实测水平位移变化过程线，同时还给出了相应时段的上游水位和坝址气温变化过程线。

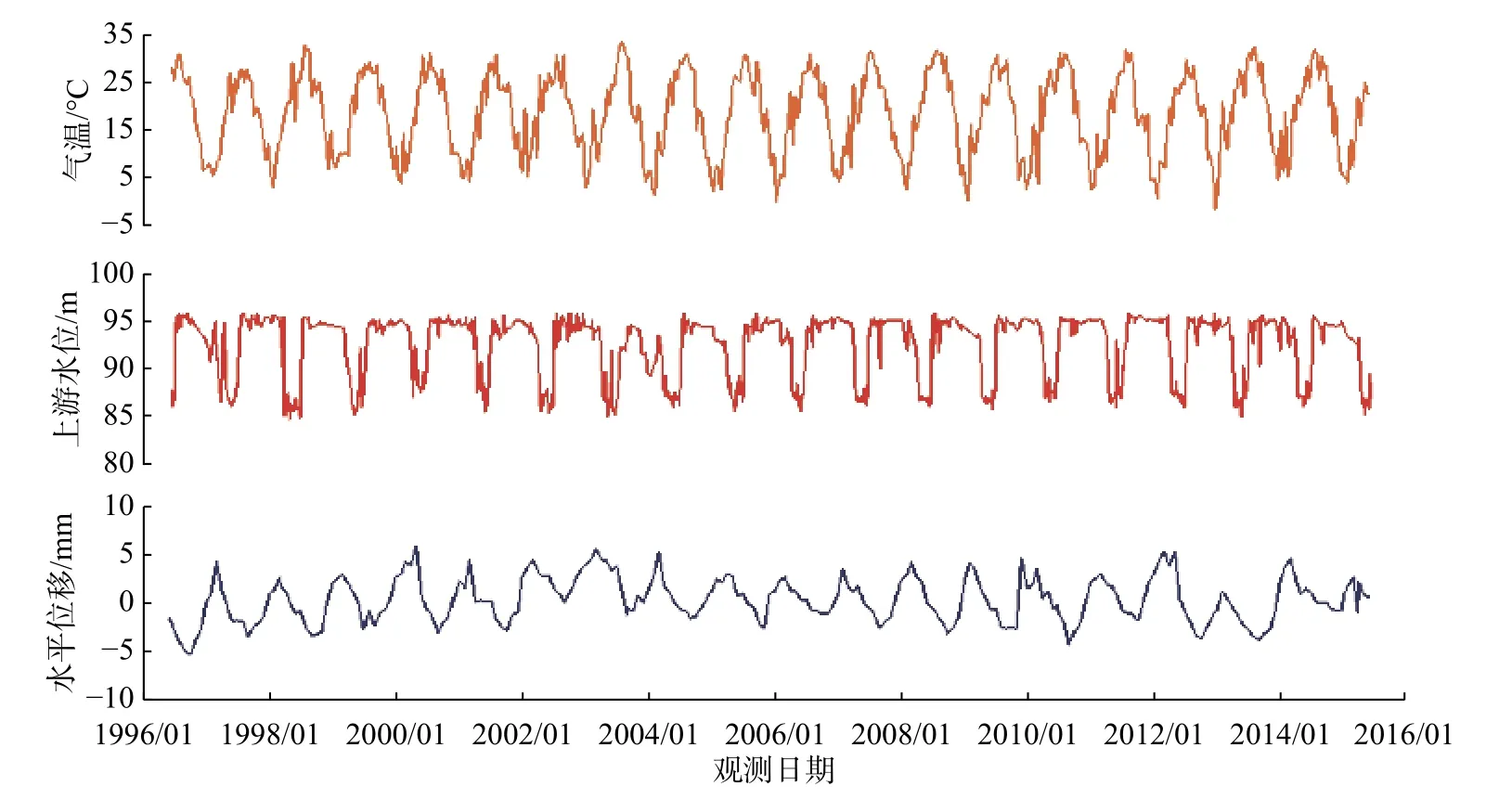
图 1 EX406 测点实测水平位移及相应环境量变化过程线Fig. 1 Process lines of measured horizontal displacement for EX406 measuring point and corresponding environmental quantity

由于坝顶水平位移向下游方向过大或向上游方向过大均认为大坝有可能不安全，因此，水平位移属于双向监控的效应量，需要分别确定向下游方向的监控指标和向上游方向的监控指标。

2.1 阈值的确定

EX406 测点水平位移监测序列{x1,x2,···,xn}中，样本标准差S=1.19 mm。首先确定下游方向的阈值。根据水平位移的观测精度，选取阈值递增序列的步长h=0.01 mm；已有的理论分析[11]表明，取尾部样本数目为样本总规模的10%～30%时，对应的阈值构建的超出量yj序列的条件分布函数FT(y)收敛于广义帕累托分布，则可据此确定初始阈值。对10%～30%的范围，当测值序列样本总规模较小时，为充分利用监测信息，可选取较大的比例值。本文实例中取为30%。

选取初始阈值后，将测值序列中的第二大值作为最大阈值，由此得到EX406 测点阈值序列{T1,···,Tj,···,TN}={2.00 mm,2.01 mm,···,5.79 mm}，进而得到超出量序列{y1,y2,···,yNT j}，其中NTj为 阈值Tj对应的超出量样本数。

采用矩估计法对广义帕累托分布参数 ξTj和 σTj进行估计，求出超出量分布函数FTj(y)及总体分布函数F(x)的表达式。在显著性水平α 分别为4.5%和0.3%的情况下，由式（3）计算每个阈值Tj对应的预警值x4.5%Tj和x0.3%Tj。

根据3σ准则对阈值序列进行筛选，选定cj最接近于0 时的阈值为向下游方向水平位移的最合理阈值；同理可确定EX406 测点向上游方向水平位移的阈值。相应计算结果如表1 所示。

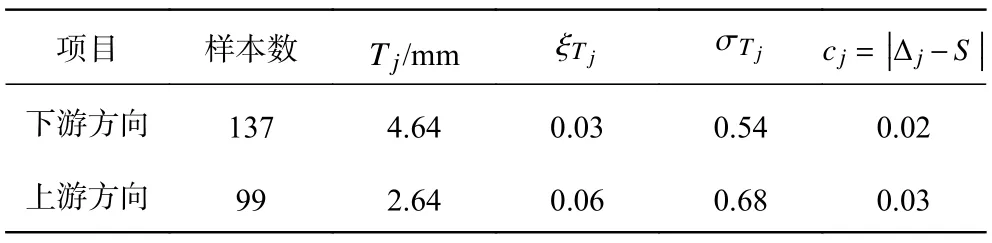
表 1 EX406 测点POT 模型计算参数Tab. 1 Calculation parameters of EX406 measuring point in POT model

2.2 监控指标的拟定

分别以显著性水平α为4.5%和0.3%的水平位移作为监控指标中的警戒值x4.5%和危险值x0.3%，上下游方向历史最大值分别为6.17 和4.93 mm；上下游水平位移的警戒值x4.5%分别为7.69 和7.75 mm，危险值x0.3%为8.90 和6.97 mm。

2.3 改进方法的验证

为验证改进方法所确定的阈值的合理性，以EX406 测点向下游水平位移为例，采用超出量均值函数图法确定阈值。根据下游水平位移的最大值和最小值，选取（0，7 mm）为阈值的取值区间，以0.01 mm为间隔求得相应的超出量均值，绘制超出量均值函数图，如图2。

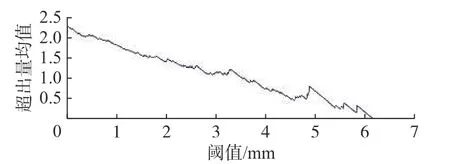
图 2 超出量均值函数Fig. 2 Mean value function plot of excesses

由图2 确定阈值T时，主要考虑两个原则。一是为满足广义帕累托分布，阈值T取值应在总样本由大到小排列的前30%以内；对EX406 测点，按由大到小排序时，30%总样本对应的测值为2.01 mm，因此阈值T应大于2.01 mm。二是基于超出量均值函数图法的基本原理，取图中曲线拐点对应的数值为阈值T。对图2 中的测值大于2.01 mm 的曲线段中有2 个比较明显的拐点，第1 个拐点出现在3.2 mm 处，第2 个拐点出现在4.6 mm 处，即图2 出现了多拐点的情形，此时需要研究者根据自身经验来确定，这也正是超出量均值函数图法的主要缺点。图2 中，鉴于4.6 mm 处的拐点相对更明显，更能满足前述的广义帕累托分布对阈值的要求，因此综合确定EX406 测点下游方向水平位移的阈值T=4.6 mm，并据此可计算得到下游方向水平位移监控指标的警戒值x4.5%Tj=7.13 mm，危险值x0.3%Tj=8.46 mm。

按超出量均值函数图法确定的EX406 测点的阈值为4.6 mm（图2）；按本文改进方法确定的EX406 测点的阈值为4.64 mm（表1）。两种方法所确定的阈值T基本接近，但超出量均值函数图法需要根据图形的形态通过人工判断，受主观因素影响较大，精度较低；改进方法通过计算机程序自动识别阈值，属于客观方法，阈值确定的精度较高，所拟定的监控指标也更为合理。

3 结 语

（1）将大坝监测效应量视为一种随机变量，基于以极值理论为基础的POT 模型，利用概率论中著名的3σ准则，对POT 模型阈值确定方法进行了改进，实现了最合理阈值的计算机自动识别，既降低了传统POT 模型法拟定大坝效应量监控指标的主观性，减轻了随机误差的影响，又增强了POT 模型法的应用前景。

（2）合理确定阈值是POT 模型的关键。基于本文的研究，在寻求新的最合理阈值确定方法时，建议遵循如下思路：设定一个初始阈值和步长，构造一个阈值递增序列，然后确定一种收敛准则，如本文提出的3σ准则，使得阈值收敛于最合理阈值。其中，在初始阈值的确定时，应使得由初始阈值形成的超出量序列的条件分布收敛于广义帕累托分布；在收敛准则的确定时，应使得收敛准则满足计算程序的可量化原则。

（3）POT 模型的理论基础为概率论，因此其本质上属于一种基于历史测值和统计理论的经验模型。采用POT 模型法拟定监控指标时，所使用的测值序列应属于满足独立同分布的随机数据序列。当大坝监测效应量受环境量和工程运行性态等因素的影响导致测值序列中存在较大的观测误差或存在明显尚未收敛的趋势性变化时，测值序列就可能不满足独立同分布条件，此时不宜采用POT 模型法拟定大坝监控指标。