土工膜界面动力剪切特性数值模拟及应用
岑威钧 ,盛希璇,温朗昇
(1. 水能资源利用关键技术湖南省重点实验室,湖南 长沙 410014;2. 河海大学 水利水电学院,江苏 南京 210098)
土工膜是一类柔性薄膜材料,其自身物理力学特性与下垫层土石料差别较大,用于(较)高土石坝坝面防渗时,需要考虑静动力条件下两者之间的相互作用效应,即土工膜界面的剪切特性[1-2]。目前国内外已有一些土工膜与土体之间静力接触特性的相关研究。例如,Wu 等[3]通过直剪试验分别对复合土工膜与砂砾石及与聚合物混合碎石接触面剪切特性进行研究,试验结果表明前者接触面的剪应力与剪切位移呈非线性关系,而后者近似呈非线性-理想弹塑性关系。童军等[4]对复合土工膜-砂砾料垫层界面进行直剪试验研究,发现界面的摩擦因子与粗颗粒含量、相对密度呈正比。Cen 等[5-8]对土工膜与细砂、砂砾石、土工布、无砂混凝土等工程中常用的垫层材料开展了一系列界面直剪试验,得到了各类界面的抗剪强度指标,并建立了土工膜-细砂界面静力接触面数学模型;同时,对土工膜与砂砾石循环剪切特性进行较深入研究,建立了动力接触面本构模型。本文简要介绍土工膜-砂砾石界面循环剪切试验成果及相应的本构模型,通过在ADINA软件中的二次开发,对土工膜界面循环剪切试验进行数值模拟验证,在此基础上进一步开展土工膜防渗土石坝的抗震分析应用,得到地震作用下考虑界面动力剪切作用的坝面防渗土工膜的动力变形和应力结果。
1 土工膜界面循环剪切试验
对室内土石料大型叠环式单剪试验仪进行改装,使之适用于土工膜界面循环剪切试验。试验采用的材料、试验方案、试验控制参数,以及得到的试验数据、数学模型及参数确定详见文献[6-7]。循环剪切试验设置50、100 和200 kPa 等3 组竖向压力。剪切位移幅值分别取1.0、2.0、3.0、4.0 和5.0 mm。试验结果表明:各级竖向压力下,随着剪切位移的增加,剪应力逐渐增大,但增大的幅值逐渐减小,呈非线性特性。不同剪切位移幅值下,一次循环剪切形成的滞回圈总体上关于原点呈中心对称分布。同一竖向压力下,随着剪切位移幅值的不断增加,滞回圈逐渐由狭长变得饱满,同时剪应力峰值的连线(即主干线)也逐渐向剪切位移轴倾斜,表明接触面的割线剪切刚度随着剪切位移幅值增加逐渐减小。相同位移幅值时,竖向压力越大,剪应力也越大,相应的滞回圈亦越大。
严格来说,动力本构建模时应考虑施加荷载的循环性及加载速率等因素。由于较大的加载速率对试验仪器要求比较高,因此室内也常用循环剪切试验模拟接触面的动力特性(常见的地震荷载属于低频往复振动),根据低速循环剪切试验建立的本构模型亦可认为属于动力本构模型范畴。本文借鉴混凝土与土接触面模型[9]及土动力学中黏弹性模型建模思路[10-11],采用等效剪切劲度和阻尼比来刻画土工膜界面动力剪切特性。根据试验所得滞回圈及主干线,建立如下土工膜界面循环剪切劲度表达式[7]:

式中:Kmax为最大剪切模量,Kmax=K1γw(σn/Pa)n1,其中 K1和 n1为无因次系数, γw为水的重度, Pa为大气压强, σn为法向应力; Rf为破坏比; u为剪切位移; δc为循环剪切摩擦角。
循环剪切试验得到的滞回圈代表着一个循环加载过程中的能量损失,可用等效阻尼比 λ刻画这一能量耗损。图1 给出了不同竖向压力下土工膜界面等效阻尼比试验点[7]。由图1 可见,同一竖向压力作用下,阻尼比随剪切位移不断增长,但增幅变小,最终趋于稳定。
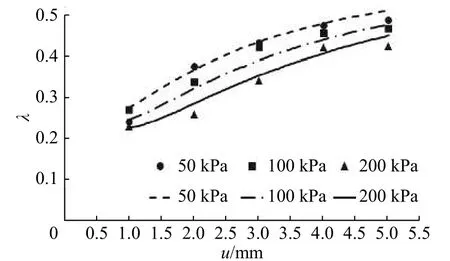
图 1 土工膜-砂砾料界面阻尼比与剪切位移关系Fig. 1 Relationship between damping ratio and shear displacement of geomembrane-gravel interface
为了考虑上述试验现象和主要影响因素,建立了如下反映压力相关的阻尼比数学模型[7]。
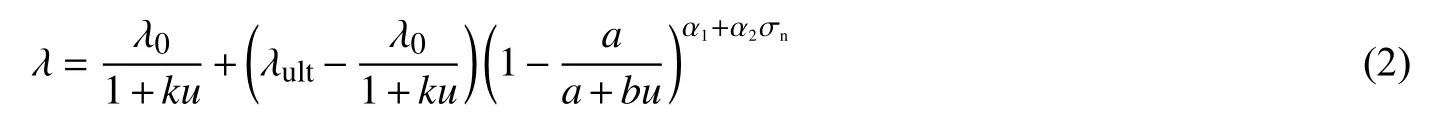
式中: λ0和λult分别为初始阻尼比和极限阻尼比; k、 α1和 α2为模型参数;a=1/K1γw(σn/Pa)n1,b=Rf/σntanδc。
根据图1 中试验数据,可以求得上述模型的相关试验参数, λ0、λult、 k、 α1和 α2分别为0.32、0.72、1.25、1.84 和0.012 4[7]。图1 中给出了由式(2)得到的拟合曲线,与试验点吻合较好,验证了所建阻尼比模型的模拟能力。
2 界面动力剪切特性的有限元模拟
对上述土工膜-砂砾料界面循环剪切试验进行有限元数值模拟,计算模型尺寸同实际试验值,即上盒中为直径300.0 mm、高度180.0 mm 的砂砾石圆柱形试样;下剪切盒为长方体,其边长360.0 mm×360.0 mm,高度120.0 mm。在土工膜和砂砾料之间设置薄层接触单元,厚度为5.0 mm。切向剪切劲度采用式(1),阻尼比采用式(2)计算。上剪切盒内土石料试样周边设置三向固定约束,下剪切盒为刚性材料,采用弹性模量设置大值进行模拟。对下剪切盒施加往复位移荷载,具体工况设置同模型试验,即往复位移幅值分别取1.0、2.0、3.0、4.0 和5.0 mm。
图2 给出了计算模型接触面中心节点处竖向压力50 kPa 和200 kPa 下的剪应力和剪切位移关系曲线。由图2 可见,不同压力和剪切位移幅值下各滞回圈总体上与相应的试验点吻合较好,主干线自然也吻合较好,初步验证了所建土工膜-砂砾料界面动力接触本构模型的合理性。
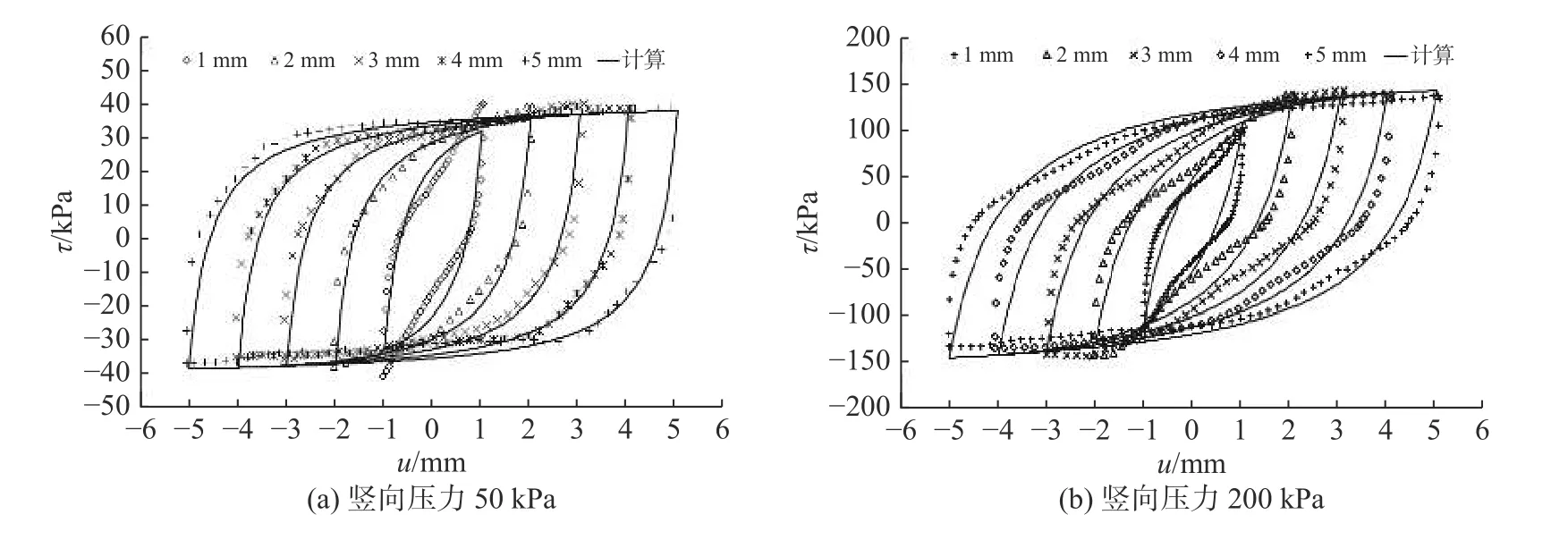
图 2 土工膜-砂砾石界面的剪应力和剪切位移关系Fig. 2 Relationship between shear stress and shear displacement of geomembrane-gravel interface
3 土工膜界面动力本构模型应用分析
3.1 计算模型与计算条件
某土工膜防渗堆石坝,坝高80 m,坝顶宽度9.3 m,上游坝坡1∶1.5,下游坝坡1∶1.8,坝面采用0.75 mm厚HDPE 土工膜防渗,土工膜上铺块石保护层,下设砂砾料垫层,计算水位78 m。大坝三维有限元计算模型节点13 006 个,单元11 704 个。在土工膜与垫层之间设置了382 个薄层接触面单元。开展大坝地震反应计算之前先要进行静力分析,其中前19 步模拟地基、坝体分级填筑、铺设坝面土工膜和保护层,以及坝面施加水荷载等静力加载过程,第20 步施加地震荷载。动力计算时,坝基采用无质量地基,地震输入采用Taft 波,将顺河向和坝轴向峰值加速度调为0.1g,竖向峰值加速度调为0.067g。静力计算时坝体材料采用邓肯E-B 模型,动力计算时采用Hardin-Drnevich 模型,相应的计算参数见表1。静动力计算时土工膜与垫层之间采用相同接触面本构模型。
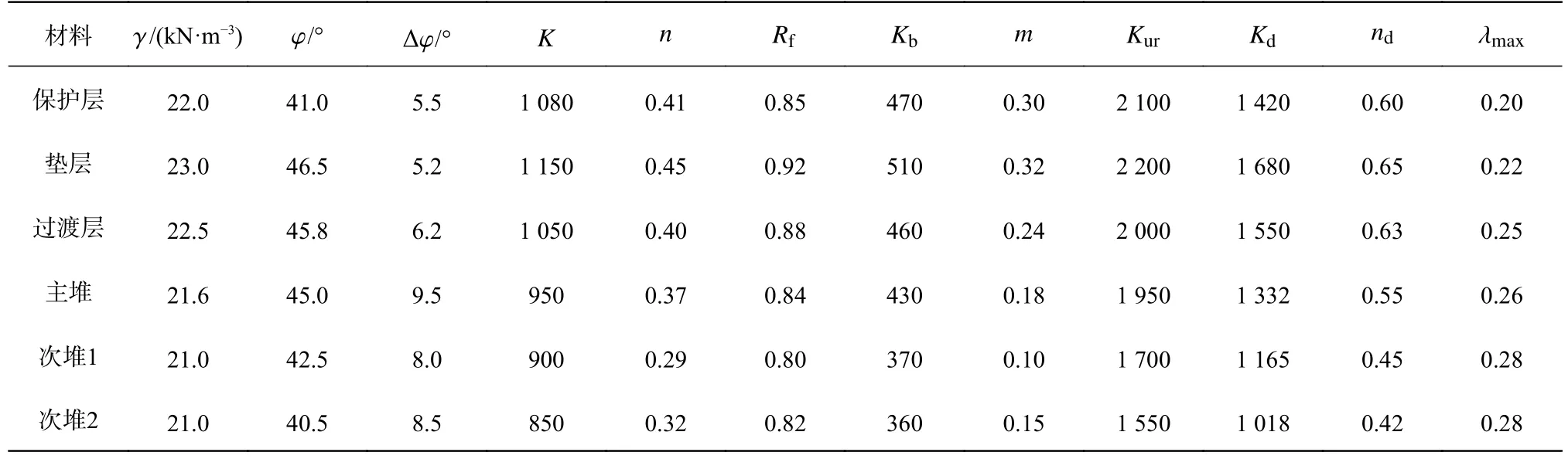
表 1 坝料静动力计算参数Tab. 1 Static and dynamic parameters of dam materials
3.2 结果分析
计算得到的坝体静、动力应力和变形结果符合土石坝一般规律,限于篇幅不再详细展示。由于接触面模型的设置主要影响土工膜的受力变形特性,因此对土工膜的相关计算结果进行重点分析。图3 为蓄水期坝面土工膜变形等值线分布图。由图3 可见,对称河谷条件下坝面土工膜变形呈左右对称分布,顺河向、竖向和总变形均沿坝高呈先增大后减小的趋势,最大值出现在河床坝段的40%坝高附近。坝轴向变形由两岸指向河床。进一步对比垫层上表面位移,发现土工膜与垫层之间发生了相对位移,说明两者之间出现了剪切滑移。由此可见,土工膜界面是否设置接触面模型对计算结果有一定影响,主要减小了土工膜的剪切位移。
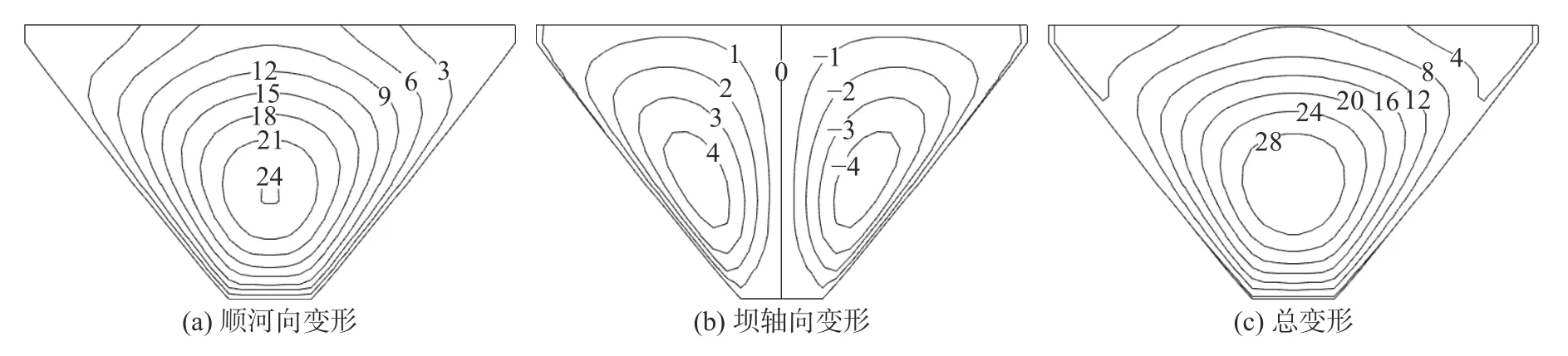
图 3 蓄水期土工膜位移分布(单位:cm)Fig. 3 Displacement distribution of geomembrane during water storage period (unit: cm)
图4 为蓄水期坝面土工膜主拉应变和主拉应力等值线分布。由图4 可见,土工膜主拉应变分布与主拉应力分布规律基本相似,最大值均位于两侧岸坡偏底部,表明受边界约束土工膜的可能受拉破坏主要集中于此。计算表明,蓄水期土工膜主拉应变和主拉应力极值分别为0.71%和0.80 MPa,远小于0.75 mm 厚HDPE 土工膜的屈服伸长率14.7%和屈服强度12.78 MPa,说明土工膜不会拉坏。与不设置土工膜接触面的结果相比,土工膜主拉应变和主拉应力极值均有所减小,这与前述的土工膜与垫层之间发生了相对剪切位移是互相吻合的。
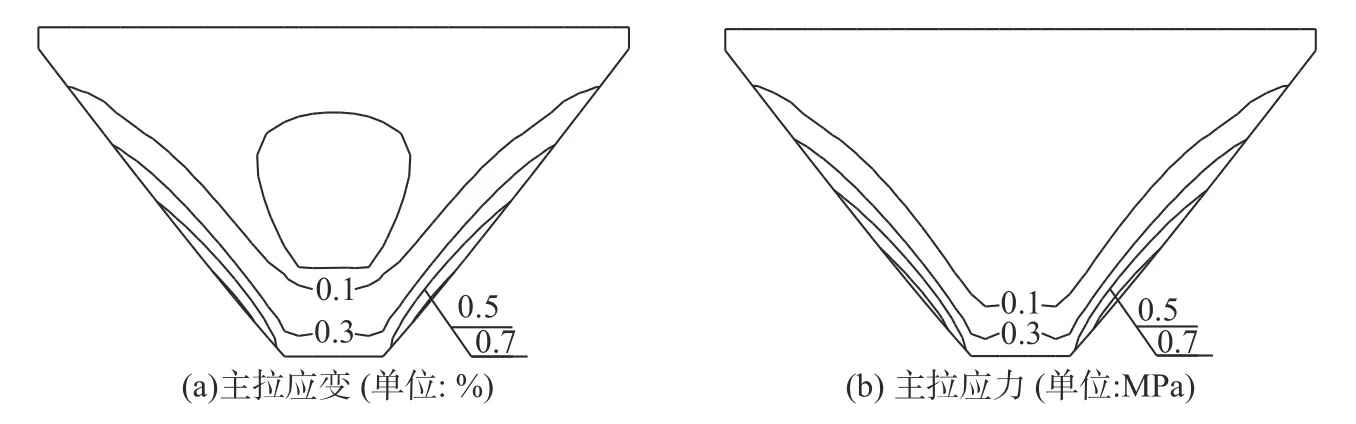
图 4 蓄水期土工膜静力主拉应变和主拉应力Fig. 4 Static principal tensile strain and stress of geomembrane during water storage period
图5 为地震作用时坝面土工膜的动位移等值线包络图(即绝对值的最大值)。由图5 可见,土工膜三向动位移沿坝高逐渐增大,在河床中央附近坝顶处达到最大值,与坝体动位移极值处相吻合。图6 为地震作用时坝面土工膜动主拉应变和动主拉应力等值线包络图。地震作用下土工膜主拉应变和主拉应力均呈现随坝高的增加先增大后减小的分布规律,最大值出现在80%坝高附近。由于在土工膜与垫层之间设置了接触面单元,地震作用时发生了相对位移,因此土工膜动主拉应变和动主拉应力值均较小,其值分别为0.05%和0.05 MPa。这与前述土工膜与垫层之间发生了剪切位移有关。设置接触面模型后,计算得到的土工膜动拉应力和拉应变均有所减小。进一步将蓄水期和地震作用下坝面土工膜的静动主拉应力进行叠加,可得到总的土工膜主拉应力包络图(图7)。由图7 可知,静动叠加后土工膜主拉应力分布规律与静力结果相似,最大值出现在岸坡偏底部,其值为0.81 MPa,小于土工膜的屈服拉伸强度。由此可见,对于土工膜防渗土石坝来说,无论静力状态还是地震作用时,应重点关注岸坡和河床底部锚固处土工膜的受力特性和工作状态,防止该区域土工膜发生局部受拉破坏。
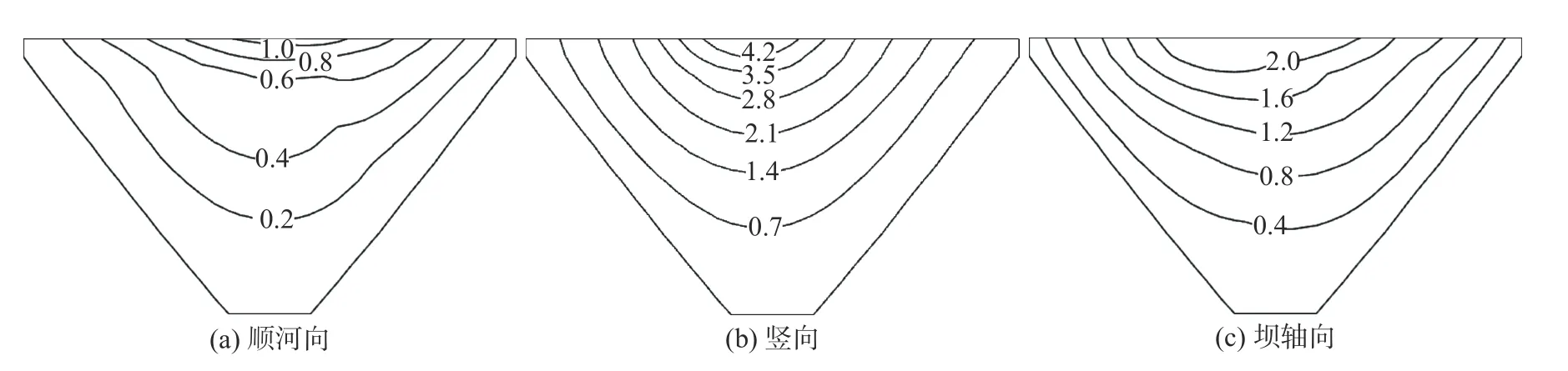
图 5 地震作用下坝面土工膜动位移包络图(单位:cm)Fig. 5 Dynamic displacement of geomembrane under earthquake (unit: cm)
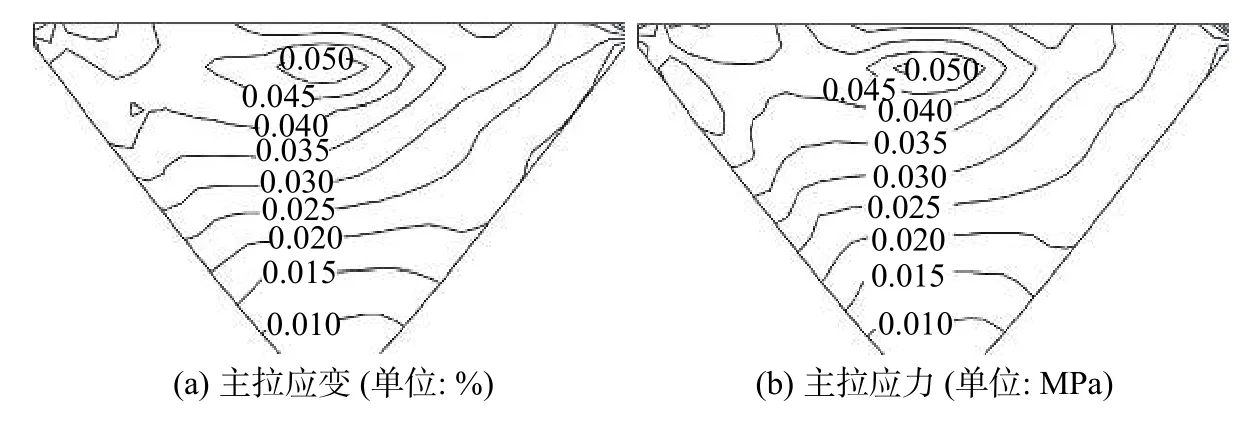
图 6 地震作用下坝面土工膜动主拉应力和动主拉应变包络图Fig. 6 Dynamic principal tensile stress and strain of geomembrane under earthquake
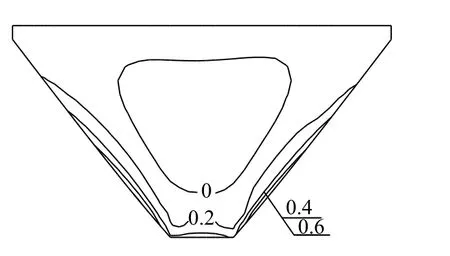
图 7 静动力叠加后土工膜主拉应力包络图(单位:MPa)Fig. 7 Principal tensile stress of geomembrane after static and dynamic superposition (unit: MPa)
4 结 语
(1)土工膜-砂砾料界面循环剪切试验表明,剪切劲度合理反映界面动力剪切的非线性特性,等效阻尼比反映界面动力剪切的滞后性。循环剪切试验的有限元数值模拟结果与试验值总体吻合较好,验证了土工膜界面动力剪切模型的合理性。
(2)土工膜防渗土石坝三维静动力有限元计算表明,蓄水期土工膜变形分布规律和极值均在合理范围。地震作用下,土工膜动位移、加速度、动拉应变和动拉应力分布规律性好。静动叠加后的坝面土工膜主拉应力分布大值区主要集中在岸坡偏底部和河床底部相锚固附近。由于土工膜与垫层之间设置了接触面单元,土工与垫层之间发生了剪切位移,因此土工膜的主拉应力总体较小,极值为0.81 MPa,远小于其抗拉屈服强度,土工膜安全可以保障。

