组合梁抗弯极限承载力参数影响分析*

代 力 江祥林 朱泽文 何雄君

(1.江西省交通科学研究院 南昌 330200； 2.长大桥梁建设关键技术及装备交通运输行业研发中心 南昌 330200；3.武汉理工大学交通学院 武汉 430063)

钢-混组合结构是在钢结构与钢筋混凝土结构上发展而来的新型结构，这种组合结构具备承载力高、刚度大、截面尺寸小，以及施工快速等优点，近几十年来，钢-混组合结构的发展速度很快，实践证明钢-混组合结构能较好地满足现代结构的功能需求[1]，而抗弯极限承载力作为组合梁重要的承载技术指标值得深入研究。

Kemp[2]对采用工字型钢梁的组合梁进行了试验研究，探究组合梁在弯曲情形下的稳定性能，分析组合梁失稳破坏时的受弯承载力和变形能力。结果表明，钢梁腹板高度、翼缘厚度、腹板厚度及翼缘宽度等参数对组合梁抗弯承载力存在较大的影响。马增[3]利用试验研究集簇式栓钉剪力连接程度对组合梁结构极限承载力、破坏形式及劈裂效应的影响。结果表明，集簇式栓钉的剪力连接程度对组合梁极限承载力影响较小。聂建国[4]也研究了相关影响因素对组合梁抗弯极限承载力的影响，近些年来，越来越多的学者关注组合梁抗弯极限承载力的优化措施，本文基于此，开展组合梁抗弯极限承载力参数影响分析。

1 有限元模型

为准确模拟结构的非线性行为，本文利用ABAQUS进行组合梁受弯过程的非线性模拟。

1.1 材料参数

1) 混凝土本构。单轴应力-应变关系式的上升段采用GB 50010-2010 《混凝土结构设计规范》中公式[5]，下降段采用Hongnestad的处理方法，对应计算公式如下。

当εc≤εo时

(1)

当εo<εc≤εcu时

(2)

式中：σc为混凝土的压应变为εc时的压应力；fc为混凝土的抗压强度设计值；εo为当压应力达到fc时，混凝土对应的压应变；εcu为极限压应变，取值为0.003 3。

2) 钢材本构。钢材的本构模型包括理想弹塑性模型、双折线模型，以及完整曲线模型，本构模型见图1。

图1 钢材本构模型

由于理想弹塑性模型在保证计算精度时也能降低计算量，因此钢梁本构模型取用理想弹塑性模型。其中：钢梁弹性模量取值为2.06 GPa；泊松比取值为0.3；屈服强度取值为345 MPa。

3) 栓钉本构关系。栓钉的本构关系通常选用三折线模型[6-7]，数学表达式为

(3)

式中：σs与εi分别为等效应力与应变；fsy与εsy分别为屈服强度与屈服应变；fu与εsu分别为极限强度及达到极限强度时的应变；Ess为栓钉的弹性模量，取值为206 GPa。

1.2 模型建立

在过去的组合梁结构建模中，栓钉通常选择多自由度的弹簧进行模拟[8]，本文采用精细化建模，建立栓钉的实体单元来模拟钢梁与混凝土板的实际接触，建模部件主要包括钢梁、混凝土板、栓钉。各部件均采用8节点的三维实体线性减缩积分单元(C3D8R)，并且注意到在模型运行中若不加入竖向加劲肋容易造成结构局部失稳，因此在支座处按实际情况添加竖向加劲肋，一般不能简化，单元也为C3D8R实体单元。

工字钢顶板-混凝土、栓钉-混凝土界面接触，以及栓钉的模拟方式均影响钢-混凝土组合梁界面滑移的大小，从而影响组合梁的整体力学性能。定义界面的面面接触，法向采用软件默认的“硬”接触，切向采用罚函数接触，摩擦系数为0.4[9]；栓钉根部底面与钢板“Tie”固结，并以“Embedded”方式嵌入顶部混凝土板，模型见图2。

图2 组合梁模型

2 钢梁参数对组合梁抗弯极限承载力的影响

采用控制变量的单参数研究方法探究钢梁强度、腹板厚度、腹板高度及翼缘板厚度对组合梁抗弯承载力的影响，组合梁截面尺寸见图3，标准尺寸数据：bf1=bf2=400 mm，b=2 000 mm，tw=12 mm，h=180 mm，t1=t2=12 mm，h1=634 mm。

图3 组合梁截面尺寸参数

在探究钢梁强度对组合梁抗弯极限承载力的研究中，以钢梁强度等级为变量，分别取强度为235，290，345，390 MPa的钢梁进行研究。以腹板厚度tw为研究参数时，tw分别取4，8，12，16 mm；以腹板高度h1为研究参数时，h1分别取360，460，560，660 mm；以上、下翼缘厚度为研究参数时，分别取6，8，10，12 mm厚度的钢梁进行研究。荷载-挠度曲线及极限承载力随钢梁参数变化数值见图4，钢梁各参数对抗弯极限承载力的影响折线见图5。

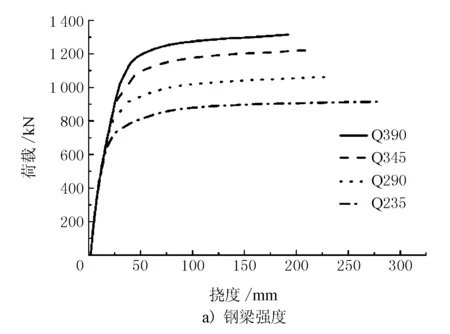
图4 不同钢梁参数因素下的荷载-挠度曲线

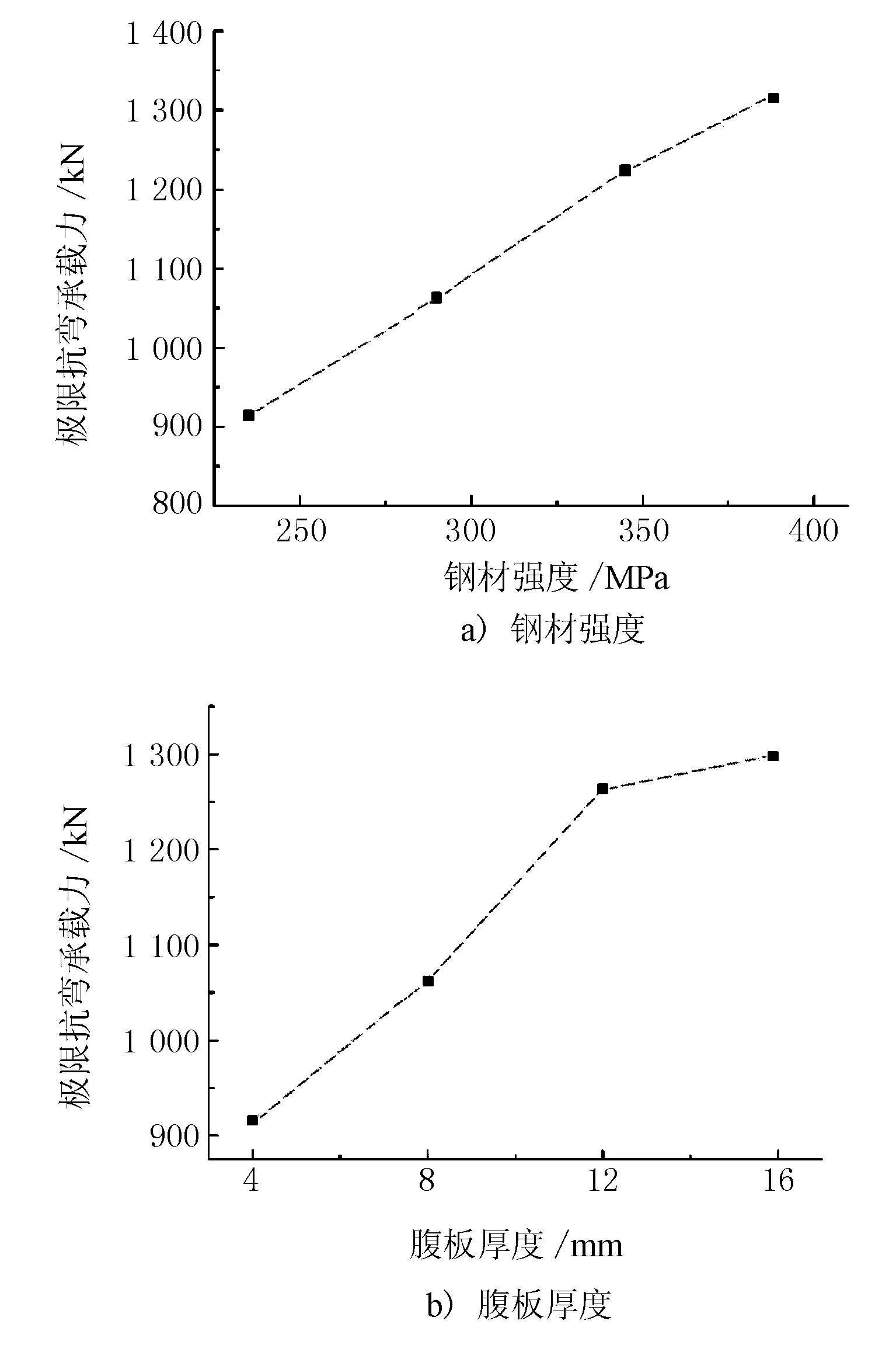
图5 钢梁各参数对抗弯极限承载力的影响折线

由图4、图5可见，上述钢梁参数对组合梁抗弯极限承载力均有较大的影响，当钢梁强度由235 MPa提升至390 MPa时，组合梁结构的极限抗弯承载力分别在235 MPa基础上提升了16%，33.9%，43.7%；钢梁腹板厚度由4 mm提升至16 mm，组合梁的极限承载力提升了40.9%，同时腹板厚度对组合梁的初期刚度也存在较大影响，在相同荷载下腹板厚度越大，挠度越小；当钢梁高度由360 mm增加至660 mm时，组合梁抗弯承载力在高度为360 mm的基础上分别增加了16.6%，27.5%，50.8%，同时组合梁初期刚度与钢梁腹板高度存在较大关系，加载初期组合梁的刚度随钢梁高度的增加而增加；钢梁翼缘厚度由6 mm上升至12 mm组合梁抗弯极限承载力分别在6 mm翼缘厚度组合梁的基础上增加了8.6%，21.7%，32.6%，同时加载初期钢梁翼缘厚度与组合梁刚度也存在联系，提升钢梁上下翼缘厚度有利于提高组合梁刚度。

3 混凝土板参数对组合梁抗弯极限承载力的影响

为探究混凝土强度及混凝土板板厚对组合梁抗弯承载力的影响，选取C30、C40、C50、C60混凝土及厚度为160，180，200，220 mm的混凝土板进行数值模拟分析。数值模拟所得荷载挠度曲线及极限承载力随钢梁参数变化见图6、图7。

图6 不同混凝土强度及厚度下的组合梁荷载-挠度曲线

图7 不同混凝土参数对抗弯极限承载力的影响折线

由图6、图7分析可知，加载初期混凝土板强度几乎对组合梁刚度无影响。同时当混凝土强度等级由C30提升至C60时，组合梁抗弯极限承载力仅仅提升了7.4%，在所考虑范围内混凝土强度等级对组合梁极限承载力影响不明显，这主要是由于组合梁破坏主要由跨中截面控制，当钢梁已经出现破坏，但是混凝土板却未完全压碎，混凝土自身材料性能距离破坏还有足够的空间，即使配置再高强度等级的混凝土，由于混凝土的材料性能难以发挥，因此难以对组合梁极限承载力提升做出贡献。

同时当混凝土板厚度由160 mm提升至220 mm时，组合梁抗弯承载力提升了20.4%，可见在工程设计中增加混凝土板厚度是提升组合梁抗弯极限承载力的有效途径。

4 栓钉参数对组合梁抗弯极限承载力的影响

选取直径为13，16，19，22 mm的栓钉进行数值模拟，数值模拟所得荷载挠度曲线显示极限承载力随钢梁参数变化见图8。由图8可见，在加载初期栓钉直径与组合梁刚度有较大关系，增大栓钉直径有利于提升组合梁刚度。同时当栓钉直径以3 mm为梯度由13 mm上升至22 mm的时候，组合梁的极限抗弯承载力分别在13 mm的基础上增加了11%，23.4%，29%，由此可见在所考虑范围内栓钉直径可以影响组合梁的极限抗弯承载力。

图8 栓钉直径影响下的组合梁荷载-挠度曲线

5 结语

本文通过ABAQUS对组合梁进行了关于极限承载力的参数影响分析，分析了钢梁参数、混凝土桥面板参数，以及栓钉参数对组合梁承载力的影响，主要结论如下。

1) 钢梁参数对组合梁极限抗弯承载力的影响显著，这是由于组合梁在所考虑范围内破坏由跨中截面控制，而跨中率先出现破坏的是钢梁。其中钢梁强度由235 MPa提升至390 MPa时，组合梁极限承载力提升了43.7%，钢梁腹板厚由4 mm提升至16 mm时，组合梁极限承载力提升了40.9%，钢梁腹板高度由360 mm提升至660 mm，组合梁极限承载力提升了50.8%，钢梁翼缘厚度由6 mm提升至12 mm时，组合梁极限承载力提升了32.6%。由此可见，在工程实践中，可通过提升上述钢梁参数从而达到提升组合梁极限抗弯承载力。

2) 混凝土桥面板参数对组合梁极限承载力的影响没有钢梁参数显著，当混凝土强度等级由C30提升至C70时，组合梁极限承载力提升了7.3%，混凝土桥面板厚度由160 mm提升至220 mm，组合梁极限承载力提升了20.4%。

3) 栓钉直径由13 mm提升至22 mm时，组合梁极限承载力提升了29%，研究结果表明增加栓钉直径能够有效提高组合梁的极限承载力。