波形钢腹板-混凝土组合箱梁扭转效应分析*
岳 阳 武志奎 李 峰 张元海
(1.甘肃路桥建设集团有限公司 兰州 730030;2.甘肃五环公路工程有限公司桥梁工程研究中心 兰州 730050; 3.兰州交通大学土木工程学院 兰州 730050)
波形钢腹板-混凝土组合箱梁是在传统混凝土箱梁高强轻质的发展需求中发展而来的,具有自重轻、结构合理等特点,在国内外桥梁工程中应用广泛。但相对于混凝土箱梁而言,波形钢腹板-混凝土组合箱梁扭转变形比较显著。所以对波形钢腹板-混凝土组合箱梁的扭转效应进行分析具有重要意义。文献[1]研究了波形钢腹板-混凝土组合箱梁扭转机理,对比了混凝土截面和钢-混组合截面2种计算原理与结果上的差异,分析了影响箱梁扭转的因素。文献[2]根据乌氏第二理论,进行了扭转效应分析,对波形钢腹板-混凝土组合箱梁桥模型的试验结果与ANSYS有限元程序分析结果进行了比较,寻求减少截面翘曲应力的方法和措施。文献[3]根据实验,结合有限元的分析方法,研究了偏心荷载下波形钢腹板-混凝土组合箱梁的力学性能。结果表明,在偏心荷载作用下产生的附加剪力是对称荷载作用时的1.5倍。文献[4]根据混凝土腹板连续刚构桥和变截面波形钢腹板连续刚构桥这2个模型,从挠度、翘曲应变、翘曲应力这3个层面对2种桥的扭转效应进行了对比分析。分析结果表明,普通混凝土腹板连续刚构桥抵抗扭转的能力比波形钢腹板连续刚构桥强。本文将传统混凝土箱梁扭转分析理论与波形腹板的褶皱效应相结合,以推导扭转双力矩和翘曲应力的计算表达式,建立约束扭转微分方程,求解方程的解,并结合算例对扭转翘曲应力、约束扭转双力矩和弯扭力矩进行分析。
1 波形钢腹板有效剪切模量及截面等效
因腹板呈波纹状,故波形钢腹板的有效剪切模量比钢板的剪切模量小。R.P.Johnson根据实验和有限元分析确认了这一点。波形钢腹板形状图见图1。
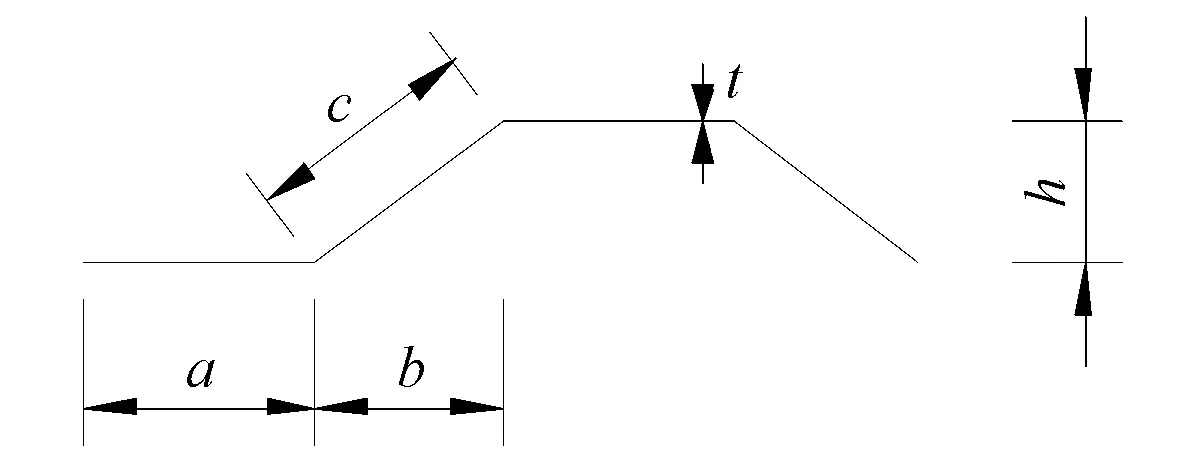
图1 波形腹板形状
有效剪切模量的计算方法见式(1)。
(1)
式中:Gs为钢材的剪切模量,Gs=Es/[2(1+υ)];υ为钢材泊松比。
箱梁受扭时其截面总剪力与剪应变是恒定的,不同材料的腹板上的剪应力和剪应变也是恒定的,根据此原则可将波形腹板厚度转换为混凝土厚度。
(2)
式中:ts为钢腹板厚度;tc为钢腹板等效为混凝土腹板之后的厚度。
2 等效后箱梁截面扭转几何特性的计算
为分析扭转效应和求解约束扭转微分方程,应先进行截面几何特性计算。本文以等效后的箱梁截面进行计算。箱梁横截面图见图2。

图2 箱梁横截面图

(3)
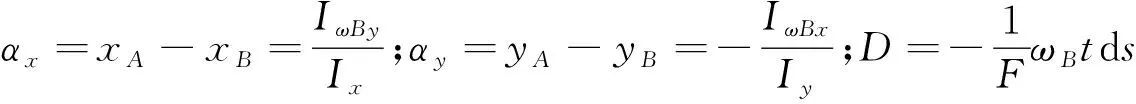
(4)
(5)
与混凝土截面相比波形钢腹板-混凝土组合箱梁截面抗扭刚度较小,所以要考虑组合截面对扭转刚度的影响,在计算时要对等效为全混凝土截面的截面抗扭惯性矩进行修正。其表达式为
(6)
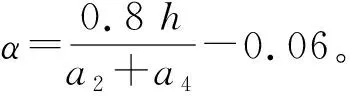
3 扭转翘曲应力
根据薄壁闭口杆件自由扭转时的纵向位移函数和乌氏第二理论假设,波形钢腹板-混凝土组合箱梁在约束扭转下纵向位移的表达式为
(7)
式中:β为波形钢腹板-混凝土组合箱梁截面的翘曲程度,是关于纵坐标z的一个待求函数。
按照箱梁截面周边不变形的假定,再根据胡克定律中应力与应变的关系可得
(8)
因为广义主扇性坐标在截面上有正、有负,所以若选取适当的起算点,可得u0′(z)=0,因而翘曲应力表达式可写为
(9)
引入约束扭转双力矩的概念。
(10)
可得约束扭转翘曲正应力表达式为
(11)
从箱梁箱壁上取出一微元体,微元应力状态图见图3。

图3 微元体应力状态图
由其微元体上力的平衡条件可得
(12)
将式(9)代入式(12),并任意选取一个起始点s=0将式(12)积分可得到约束扭转剪应力的表达式为
(13)
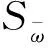
整个截面上的剪力流合成扭矩为Mz,根据内外力平衡条件
(14)
则
(15)
将式(15)代入式(14)可得
(16)
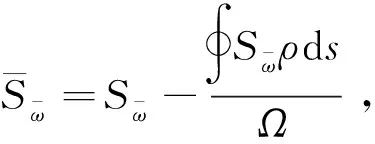
(17)
从式(17)可见,约束扭转时剪应力表达式包括两部分:①自由扭转剪应力;②翘曲正应力引起的剪应力。
(18)
将式(18)代入(17)得
(19)
4 约束扭转微分方程的建立及初参数解
通过变形条件以及β与θ之间的联系,建立波形钢腹板-混凝土组合箱梁约束扭转微分方程,见式(20)。
(20)
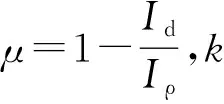
通过初参数法可解得,当构件跨内作用有外部荷载时,其初参数方程为
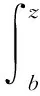
(21)

5 数值算例
算例1。选用文献[5]中两端简支的波形钢腹板组合箱梁模型为例,其横截面图见图4,简支梁跨度为l=7.5 m,顶板宽度为a4=838.3 mm,底板宽度为a2=462.5 mm,高度为H=368.75 mm,翼缘板宽度为a3=480.9 mm,顶板厚度为t4=0.112 5 m,底板厚度为t2=0.11 m,Iy=0.056 6 m4。波形钢腹板t=0.003 m,a=0.63 mm,b=0.05 m,h=0.038 m。跨中施加一偏心荷载F1=20 kN,偏心距e=0.419 5 mm,顶底板为混凝土材料其弹性模量Ec=34 GPa,泊松比为υc=1/6;钢材弹性模量Es=210 GPa,泊松比为υc=0.3。
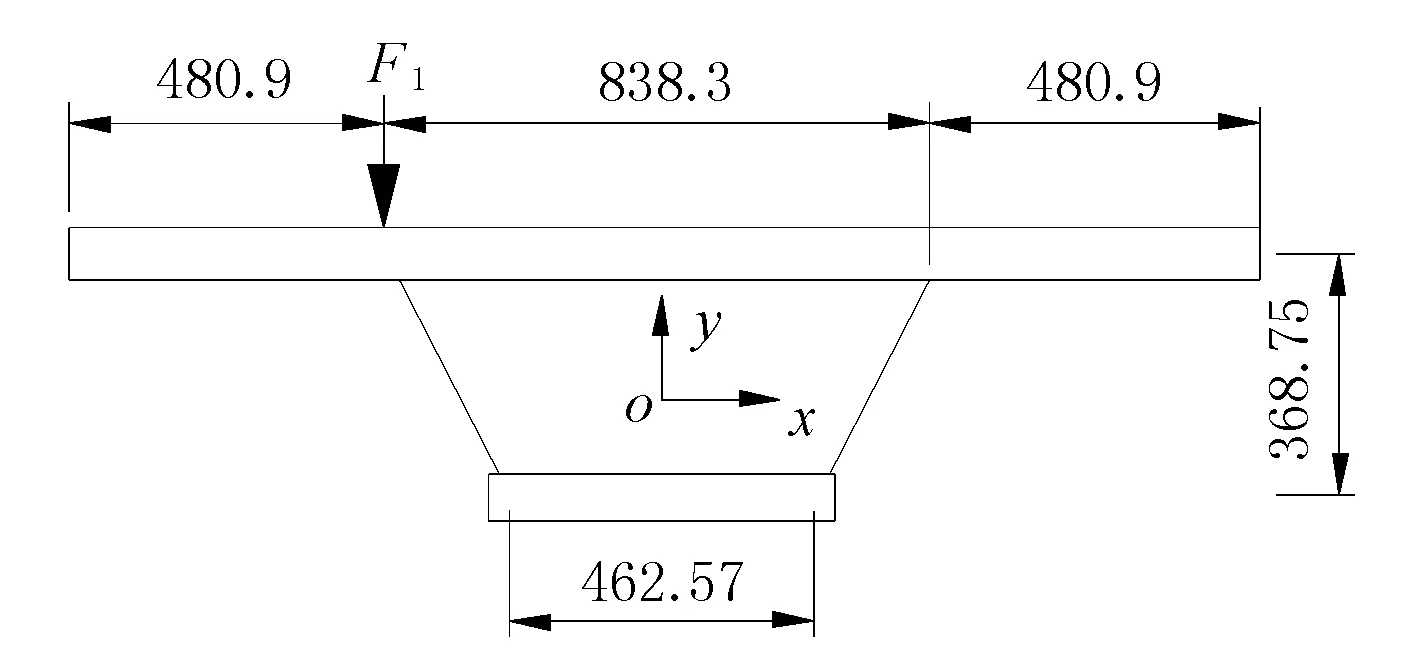
图4 箱梁横断面(单位:mm)
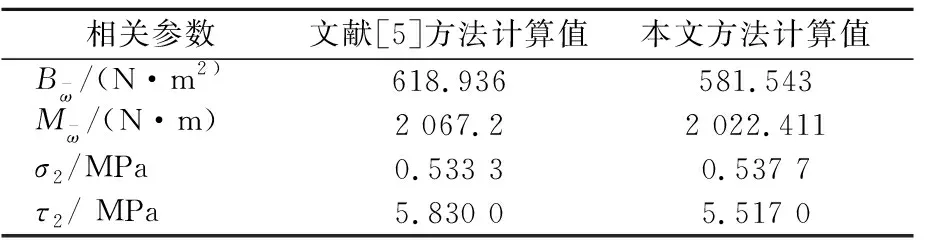
根据计算得到波形钢腹板纵向表观弹性模量Ex=0.586 9 GPa。按照截面等效公式将波形钢腹板转换成厚度为0.014 9 m的混凝土板,并计算其截面形心,求得形心位置y上=0.079 2 m,y下=0.289 5 m,转换后的截面惯性矩为Iy=0.056 6 m4,选取顶板中点为辅助极点,计算辅助扇性坐标,从而计算得到扭心的位置位于形心上方0.031 3 m处。跨中截面相关参数的计算值见表1。其中:σ2和τ2分别为腹板与底板交点处的扭转正应力和扭转剪应力。

表1 跨中截面约束扭转相关参数及应力计算值
续表1
由表1可见,本文计算所得扭转正应力与文献[5]中的计算值基本相同,但扭转剪应力稍有偏差,原因是文献[5]中计算约束扭转在悬臂板上产生的剪力流时与实际情况不符,在悬臂板自由端剪应力应为0。

表2 跨中截面扭转应力与弯曲应力比值
由表2可见,当考虑扭转效应时,跨中截面扭转翘曲正应力为弯曲正应力的1.22%,扭转剪应力为弯曲剪应力的49%。计算扭转剪应力和扭转正应力情况见图5、图6。

图5 扭转剪应力(单位:MPa)

图6 扭转正应力(单位:MPa)
由图5和图6可知,波形钢腹板组合箱梁在受到偏心荷载作用时,产生的扭转正应力主要由顶板和底板承担,扭转剪应力主要分布在钢腹板上。按照文献[5]中实验结果可知,在相同荷载情况下腹板与顶底板交点处的扭转应力实测值,与本文计算所得扭转正应力值一致。腹板上的剪应力值随腹板高度的变化规律也与实测值相符。
以此算例为对象分析了当跨中作用一集中偏心荷载时,扭转双力矩与弯扭力矩沿跨长方向的变化规律,见图7、图8。
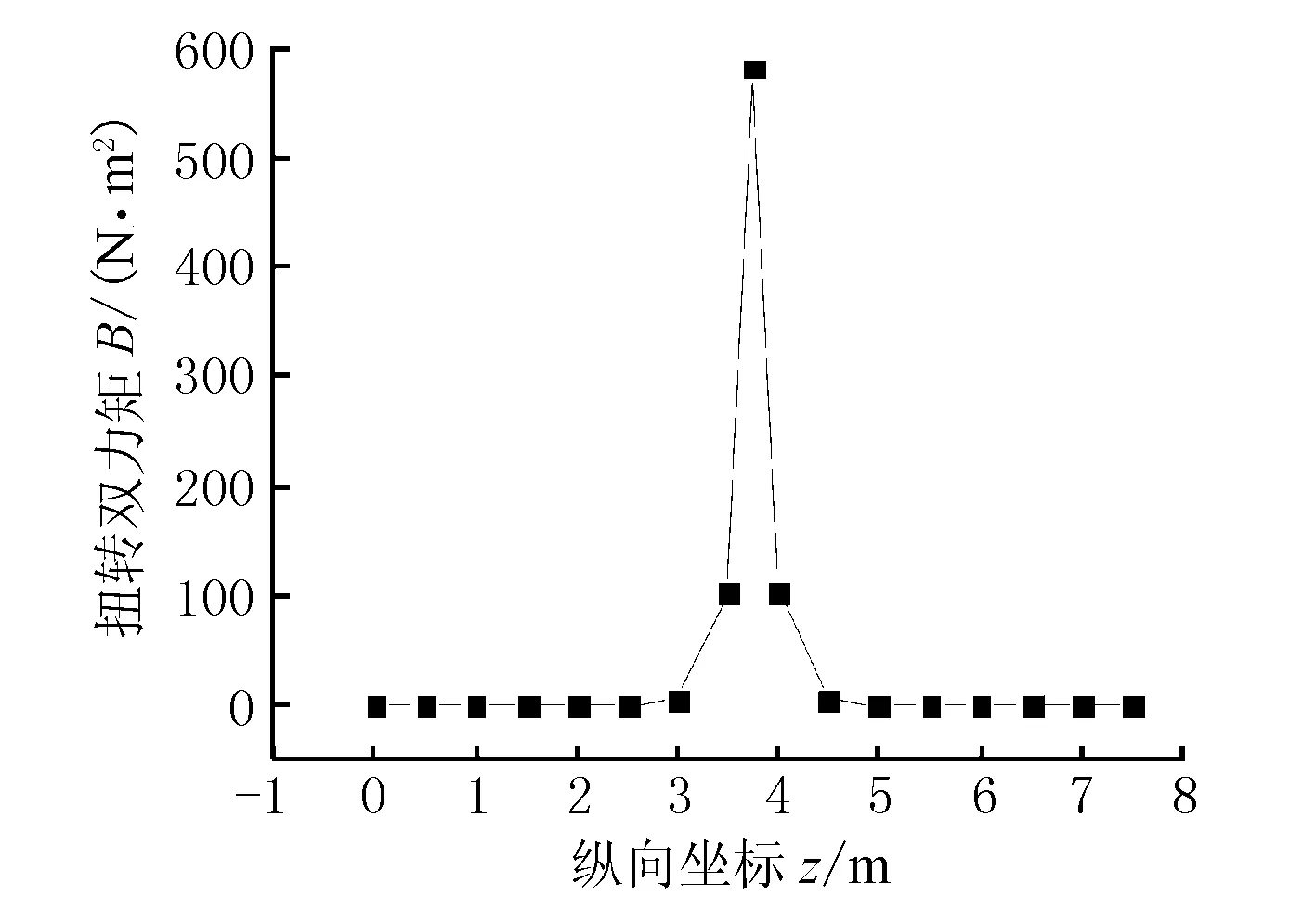
图7 扭转双力矩沿梁长的变化曲线
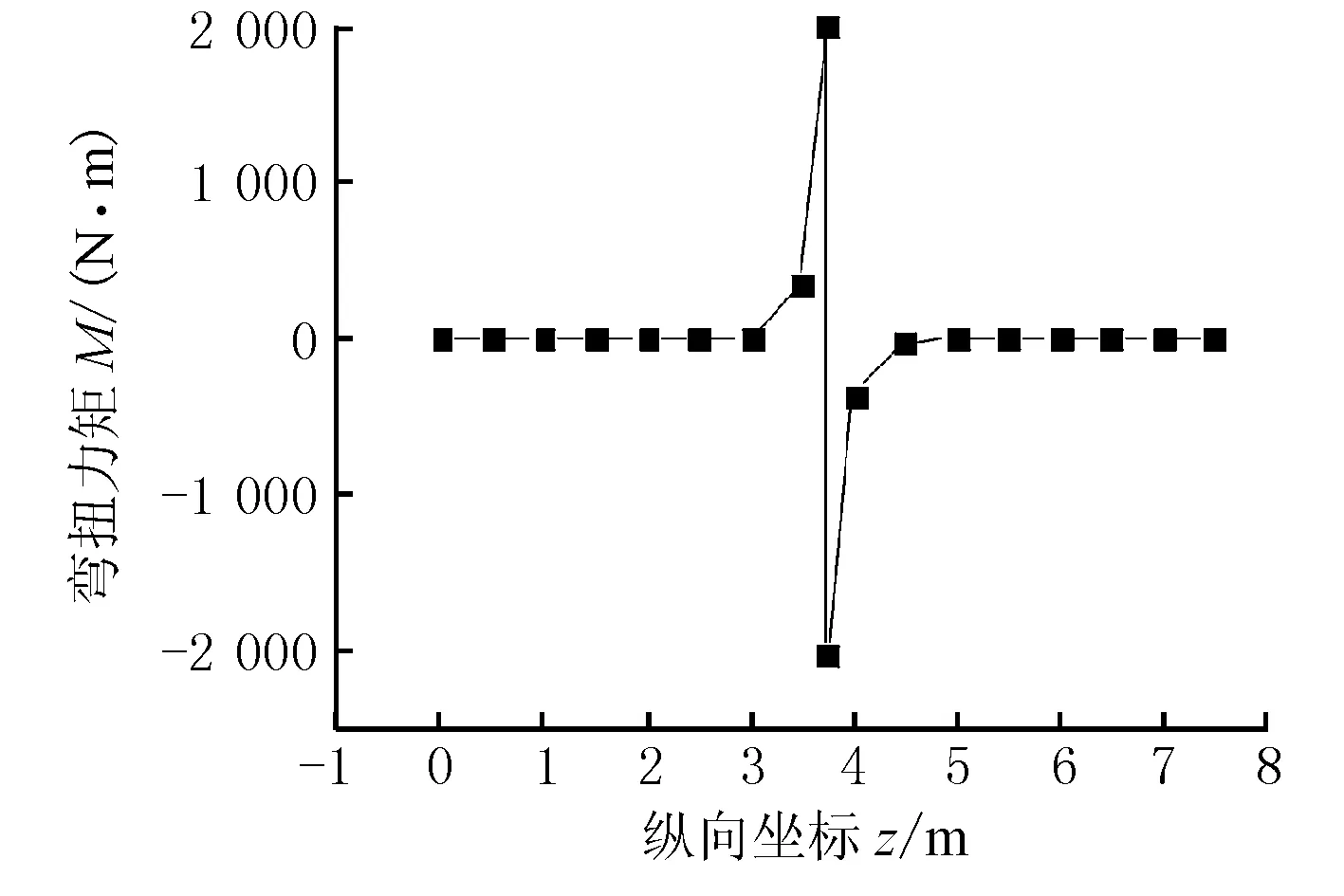
图8 弯扭力矩沿梁长的变化曲线
由图7和图8可见,当简支波形钢腹板-混凝土组合箱梁跨中作用集中偏心荷载时,扭转双力矩和弯扭力矩都在跨中产生最大值,且弯扭力矩在荷载作用处产生突变。
算例2。以文献[6]中的简支组合箱梁模型为例,进行理论计算和ANSYS软件结果对比分析。其组合箱梁计算跨径为l=9.745 m,波形钢腹板尺寸t=2.5 mm,a=62.5 mm,b=50 mm,h=37.5 mm。在跨中截面顶板腹板交点处作用有F2=85 kN的集中荷载,混凝土和钢板弹性模量分别为34.5,200 GPa,泊松比分别为0.2,0.3。箱梁截面尺寸图见图9。
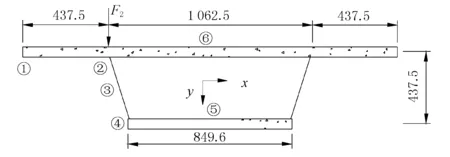
图9 组合箱梁横断面图(单位:mm)
运用ANSYS软件,采用实体单元与板壳单元模拟波形钢腹板组合箱梁的混凝土顶底板和腹板,对图9中标示的计算点①~⑥的扭转翘曲正应力和扭转剪应力进行分析计算,并与采用本文理论的计算值进行对比分析。其应力值结果见表3。
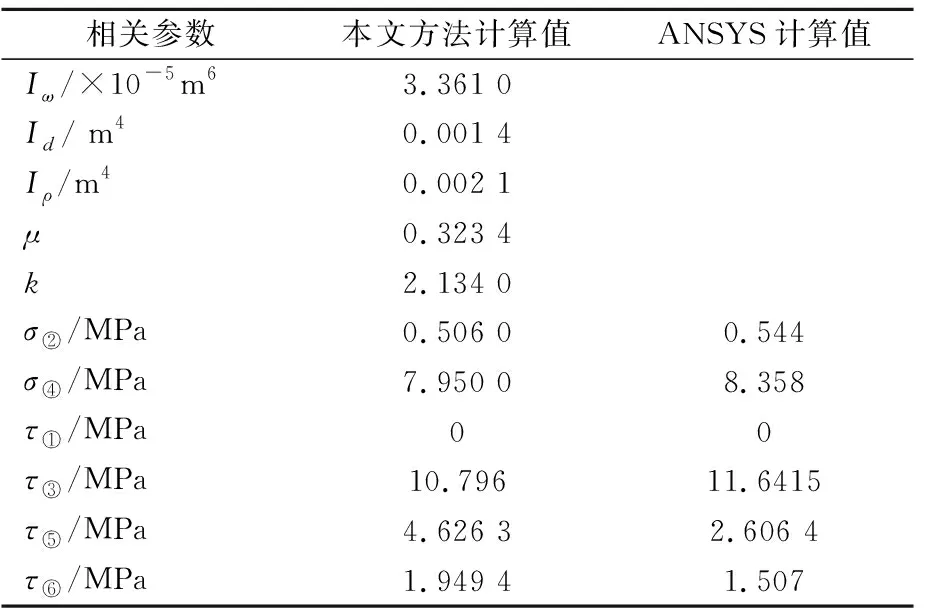
表3 跨中截面约束扭转相关参数及应力值
通过上述计算分析,可以发现本文方法计算的扭转应力值与ANSYS软件的计算值差别基本不大,误差均在10%以内。通过ANSYS软件分析,验证了算例1中悬臂板自由端处剪应力为0的结果。并且算例2的理论计算过程中,扭转双力矩和弯扭力矩的变化趋势也与算例1中的趋势相同。因此,更进一步说明本文理论对于波形钢腹板-混凝土组合箱梁扭转应力计算有较高精度。
6 结论
本文根据传统混凝土箱梁的扭转分析理论,结合波形钢腹板-混凝土组合箱梁受力特性来对扭转效应进行研究。结果表明,在跨中作用集中荷载的情况下,最大扭转翘曲正应力和最大扭转翘曲剪应力均在跨中截面产生,且扭转效应主要产生附加剪应力,本文方法对翼缘板自由端处的翘曲剪应力进行了修正,因此计算所得翘曲正应力和翘曲剪应力与文献中的实验值及ANSYS软件计算值相比,具有较高的精确性。

