基于区域校正的大面阵红外探测器非均匀性校正方法

张明杰，李 岩，马文坡，刘紫莹

（北京空间机电研究所，北京 100094）

0 引言

红外焦平面阵列（infrared focal plane array，IRFPA）的出现是红外探测器技术的一次重大飞跃，它兼具红外辐射探测和信号读出与处理功能。随着IRFPA 在各个领域应用的不断深入，红外遥感仪器也不断向着高分辨率、高灵敏度发展，焦平面阵列的规模也不断增加[1]，同时其响应的非均匀性校正也面临着巨大的挑战。

目前针对红外焦平面阵列的非均匀性问题，主要有两类校正算法，分别是基于定标的校正算法和基于场景的校正算法[2-3]。其中基于场景的校正算法虽然不需要依靠对参考辐射源进行周期性定标，从而使系统处理流程简化，但是因其本身复杂度和环境适应性的限制很难在硬件系统中实现[4]，因此实际应用中主要还是采用基于定标的校正算法[5]。

近年来各界学者对于常见的小面阵探测器（面阵规模为几百乘几百）的非均匀性校正算法的研究越来越深入，校正效果也越来越好。但是对于百万像元量级，甚至千万像元量级的大面阵红外探测器来说，由于其自身面阵比较大的特性，不同区域像元之间的响应特性差异比较大，在进行非均匀性校正时很难兼顾面阵上所有像元，导致很多针对小面阵探测器的非均匀性校正算法对大面阵探测器校正效果较差。

本文通过研究某碲镉汞（MCT）大面阵红外探测器的响应特性，并以此为依据划分区域分别进行校正处理，对于区域划分带来的不同区域之间的不均匀性，采用改进的神经网络算法进行处理。

1 传统非均匀性校正方法与校正结果分析

1.1 两点校正法

两点校正法实现的前提是红外焦平面探测器的像元是线性响应的，即探测器的实际输出与真实响应只存在一阶函数关系，用公式表示为：

式中：X代表探测器的真实响应值；Y代表探测器的实际输出值；G和D分别代表探测器的增益和偏置；(i,j)为像素的坐标值。探测器每个像元的增益系数Gij和偏置系数Dij的计算方法如下：

式中：Xij(φH)、Xij(φL)和分别为高低温度黑体均匀红外热辐射下，探测器位置(i,j)像元的原始响应输出值；PH、PL和分别为高低温度黑体均匀红外辐射下探测器最终校正输出的值，P的取值如下：

式中：M和N为红外图像的行列数；K为图像的帧数，即总共统计的次数。

1.2 二次曲线拟合算法

进行二次曲线拟合时需要选择3个定标温度点确定拟合系数，拟合系数的计算方法如下：

式中：Xij(φ1)、Xij(φ2)和Xij(φ3)分别为3个温度黑体均匀红外热辐射下，探测器位置(i,j)像元的原始响应输出值；P1、P2和P3分别为3个温度黑体均匀红外辐射下，探测器最终校正输出的值。

1.3 校正效果分析

图1所示为剔除盲元后、非均匀性校正前的黑体图像和直方图，全图的残余非均匀性为17.66%，图像的DN（digital number）值跨度达到了2000 左右。

图2所示为两点校正法校正之后的黑体图像及直方图，其中校正后全图的残余非均匀性为0.51%。从校正后黑体图像中可以看出图像左右两边的像元响应特性存在差异，从直方图也可以看出图像并不是只有一个峰，其DN值跨度在100 以内。虽然图像整体的均匀性得到了改善，但是目视效果有待改善。

图1 校正前黑体图像和直方图Fig.1 Blackbody image and histogram before correction

图3所示为二次曲线拟合校正之后的黑体图像及直方图，其中校正后全图的残余非均匀性为0.43%。从校正后的黑体图像仍然可以看出左右视场的像元响应特性存在差异，同时中间有部分区域与四周像元响应特性存在差异，另外，图像存在列向的条带噪声。从直方图中可以看出图像DN值跨度在70个DN值左右，只有一个峰，相比于两点校正算法效果更好，但图像整体上目视效果还有待改善。

由上述分析可知，不论是两点校正法还是二次曲线拟合的针对响应非线性的校正算法对于大面阵红外探测器来说，由于其本身面阵较大，各个区域间的像元响应特性差异也会被放大，导致校正效果比较差。单纯地使用某一种方法对整个面阵进行校正很难取得预期的效果，因此本文提出了一种基于区域划分的非均匀性校正算法。

2 大面阵红外探测器的校正算法

针对大面阵红外探测器，本文提出一种分区域非均匀性校正方法，首先对各个黑体图像进行整体分析，观察其原始图像的响应区间、响应线性度以及直方图等响应特性，以此选择合适的定标温度点；然后以此进行盲元检测、区域划分、非均匀性校正、区域合并、盲元补偿、神经网络校正，最后评价校正效果。本文的非均匀性校正算法的流程如图4所示。

2.1 相机响应非线性分析

本文选用碲镉汞（MCT）大面阵探测器，面阵规模为2.7 k×2.7 k，读出电路基于硅基CMOS技术，列处理电路被分成8个通道，共8 路输出。为了考查探测器每个输出通道的像元响应是否一致，首先剔除盲元后，选择第一通道和第八通道的两列像元，逐元对其辐射定标曲线进行二次曲线拟合，拟合结果如图5所示。

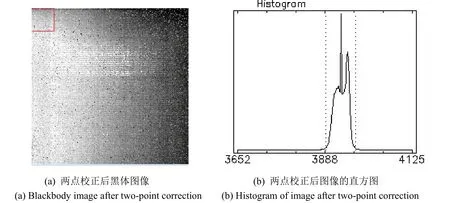
图2 两点校正后黑体图像和直方图Fig.2 Blackbody image and histogram after two-point correction

图3 二次曲线拟合算法校正后的黑体图像和直方图Fig.3 Blackbody image and histogram after quadratic curve fitting correction

图4 分区域校正算法流程图Fig.4 Flow chart of regional correction algorithm

图5 不同通道两列像元二次拟合响应曲线分析Fig.5 Quadratic fitting response curves analysis of two columns of pixels in different channels

从上述曲线拟合结果来看，这两列像元的响应特性存在一定的差异，两者都存在一定的非线性，但是其曲线的凹凸性却不一样。

为了进一步分析读出电路不同通道像元的响应特性，在剔除盲元的基础上，对探测器所有正常像元的响应曲线分别进行二次曲线拟合处理，并分析不同区域像元拟合系数的差异。

图6显示第一通道和第八通道中一列像元的二次项拟合系数的差异。

从图6中可以分析得出，一方面在不考虑个别像元二次项拟合系数偏高或偏低的情况下，一列像元的二次项拟合系数相差不大，说明该大面阵探测器同一列像元的响应比较一致；另一方面，不同通道之间二次项拟合系数存在较大的差异，二次拟合曲线存在凹凸性不一致的问题。为了进一步分析不同列像元之间二次项拟合曲线的差异，选取某几行像元的二次项拟合系数进行分析，发现不同行像元的二次项拟合系数随列的变化基本相同，如图7所示。

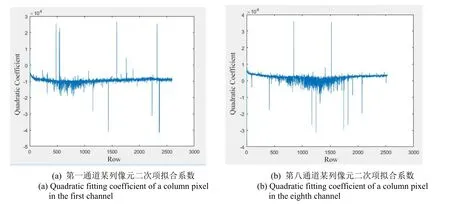
图6 不同通道两列像元二次项拟合系数差异Fig.6 Difference of quadratic fitting coefficients of two columns of pixels in different channels

图7 某一行像元的二次项拟合系数Fig.7 Quadratic fitting coefficient of a row of pixels

由此可以得出结论，首先相机响应存在非线性，另外由于相机自身的问题导致图像上不同区域的响应非线性不一致，左右视场的响应曲线凹凸性不一致，二次项拟合系数从左到右呈递增趋势。

2.2 盲元检测

红外探测器受到材料和工艺等的限制，普遍存在盲元问题，降低了红外成像系统的图像质量[6]。盲元本身不具备正常像元的响应特性，在对图像进行非均匀性校正之前，必须先将盲元的位置检测出来，不能让其参与后续的定标与校正。新版国标中关于盲元的定义是：盲元包括死像元和过热像元，死像元是指像元响应率小于平均响应率1/2的像元，过热像元是指像元噪声电压大于平均噪声电压2倍的像元[7]。

为了后续非均匀性校正的效果，盲元检测一定要充分。本文选择10个黑体定标温度点，每相邻两个温度进行一次死像元的筛选，共9次筛选，确保所有响应不正常的像元都被剔除掉。利用Matlab 编写程序剔除盲元，其中相邻两个黑体温度点的盲元检测算法的流程图如图8所示。

应用图8所示的算法对该大面阵红外探测器进行盲元检测处理，从图像中取某一列像元，用10个黑体温度定标点进行逐元的辐射定标，画出每一个像元随等效积分辐亮度的响应曲线，图9为死像元剔除前后的辐亮度响应曲线。

另外，取335 K 黑体温度下的一组30帧图像，考查其过热像元剔除前后像元响应的稳定性，如图10所示为某列像元（2704个）过热像元剔除前后的稳定性比较。

从剔除盲元后其他像元的响应特性和响应稳定性来看，本文的检测算法对于盲元的筛选比较充分，为后续非均匀性校正打下坚实的基础。

2.3 分区域校正算法

根据上述相机非线性响应的分析，将整幅大面阵图像按照读出电路的列处理电路分为八大块，分别求出每一区域的二次拟合校正曲线的系数。计算方法如下：

图8 盲元检测算法程序流程图Fig.8 Flow chart of blind element detection algorithm program

图9 死像元剔除前后响应特性比较Fig.9 Comparison of response characteristics before and after dead pixels are removed

图10 过热像元剔除前后的稳定性比较Fig.10 Comparison of stability before and after overheated pixels are removed

式中：z＝1,2,3,4,5,6,7,8；Az、Bz、Cz分别表示第z个区域的校正系数；Pz1、Pz2、Pz3分别表示3个温度黑体均匀红外辐射下，探测器第z个区域最终校正输出的值。

分区域校正完成之后，各个区域之间的均值存在一定差异，这种差异来源于为偏置系数，即最终探测器校正输出值Yz表示为：

式中：Xz为探测器第z个区域校正输出的值；Dz为偏置系数。

校正后的黑体图像及其直方图如图11所示，黑体图像8个区域呈现出比较明显的差别，在行方向存在周期性的DN值起伏。对于分区域引入的这些残余的图像噪声，本文采用基于神经网络的校正算法进行校正。

2.4 基于神经网络的校正算法

由Scribner[8]等人在1991年提出的BP（back propagation）神经网络是一种多层前馈式误差反向传播的神经网络算法，由输入层、隐含层和输出层构成，其中隐含层的作用就是给出期望值，然后用实际输出值迭代逼近，一步一步确定校正系数。经典神经网络的期望图像实际上是通过对图像进行一次空间域的低通滤波得到的，而对于分区域校正后图像呈现的周期性噪声，本文采用频率域滤波的方法得到期望图像。

首先，利用MATLAB 软件建立一个理想的只包含行方向上的周期性噪声的图像I，如图12所示；其次，将该图像I 通过傅里叶变换到频率域，比较其与理想均匀图像的频域图像之间的差别，构造一个滤波器H，使得图像I中的特定频率点置0；最后，将2.3节得到的黑体图像经过滤波器H 进行频率域滤波，得到的神经网络算法的期望图像如图13所示。

图11 分区域校正后黑体图像和直方图Fig.11 Black body image and histogram after regional correction

图12 含有特定周期性噪声的理想图像Fig.12 Ideal image with particular periodic noise

图13 改进神经网络算法的期望图像Fig.13 Expected image of improved neural network algorithm

3 实验

3.1 非均匀性校正效果评价参数

本文采用图像的时间噪声和校正后的空间噪声以及残余非均匀性作为评价指标[9]，图像的时间噪声σtemp定义为：

式中：M和N为红外图像的行列数；K为图像帧数，本文中K＝30；Vij(f)为第f帧图像像元位置(i,j)的DN值；为位置(i,j)的像元30帧响应的平均DN值。

图像的空间噪声σspat定义为：

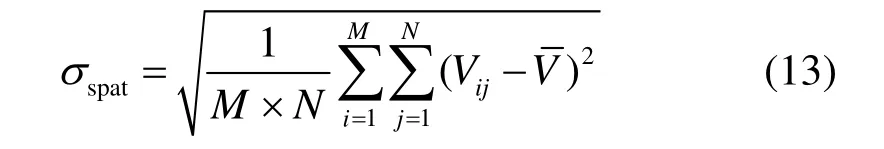
式中：Vij为单帧图像像元位置(i,j)的DN值；为单帧图像全图的平均DN值的计算方法由下式给出：

图像的残余非均匀性NU 定义为：

3.2 校正结果

选择固定积分时间、增益和谱段下的9个黑体温度图像参与本次实验，分别是：290.7 K、304.1 K、313.3 K、320.4 K、335.5 K、346.1 K、354.5 K、359.2 K、363.5 K，每个温度点包含30帧定标黑体图像。定标点选择313.3 K、346.1 K和363.5 K，并选用整体两点校正法（定标点为313.3 K和363.5 K）和整体非线性二次拟合法作为本次实验对照组。本文校正算法中的神经网络算法，经过多次实验验证，选择模板大小为11×11、迭代步长a设为0.0001、阈值设为1，此时该算法的稳定性、收敛速度以及校正效果等相对更好。

图像的时间噪声和校正前后图像的空间噪声以及残余非均匀性如表1所示。

表1统计的是整体图像的各项指标，可以看到，本文的校正算法大部分黑体温度图像其残余非均匀性已经降到了0.2%左右，空间噪声也已经小于或者逼近时间噪声。表2所示为校正前后320.4 K 温度图像局部小区域的残余非均匀性等指标。

由表2可以看出，区域为11×11时，3种方法校正后的残余非均匀性和空间噪声相差不多，随着区域变大，本文校正算法的优势也不断扩大，小区域的空间噪声经过本文算法校正后明显小于时间噪声，为后续目标检测提供了良好的环境。

经过本文的校正算法进行非均匀性校正后，图像上各个区域的像元响应情况比较一致，图14分别表示第200列像元和第2500列像元随入射积分辐亮度的响应曲线，相比于图4可以看出该算法非均匀性校正取得了很好的效果。

图15为本文的方法进行非均匀性校正之后的黑体图像和直方图。

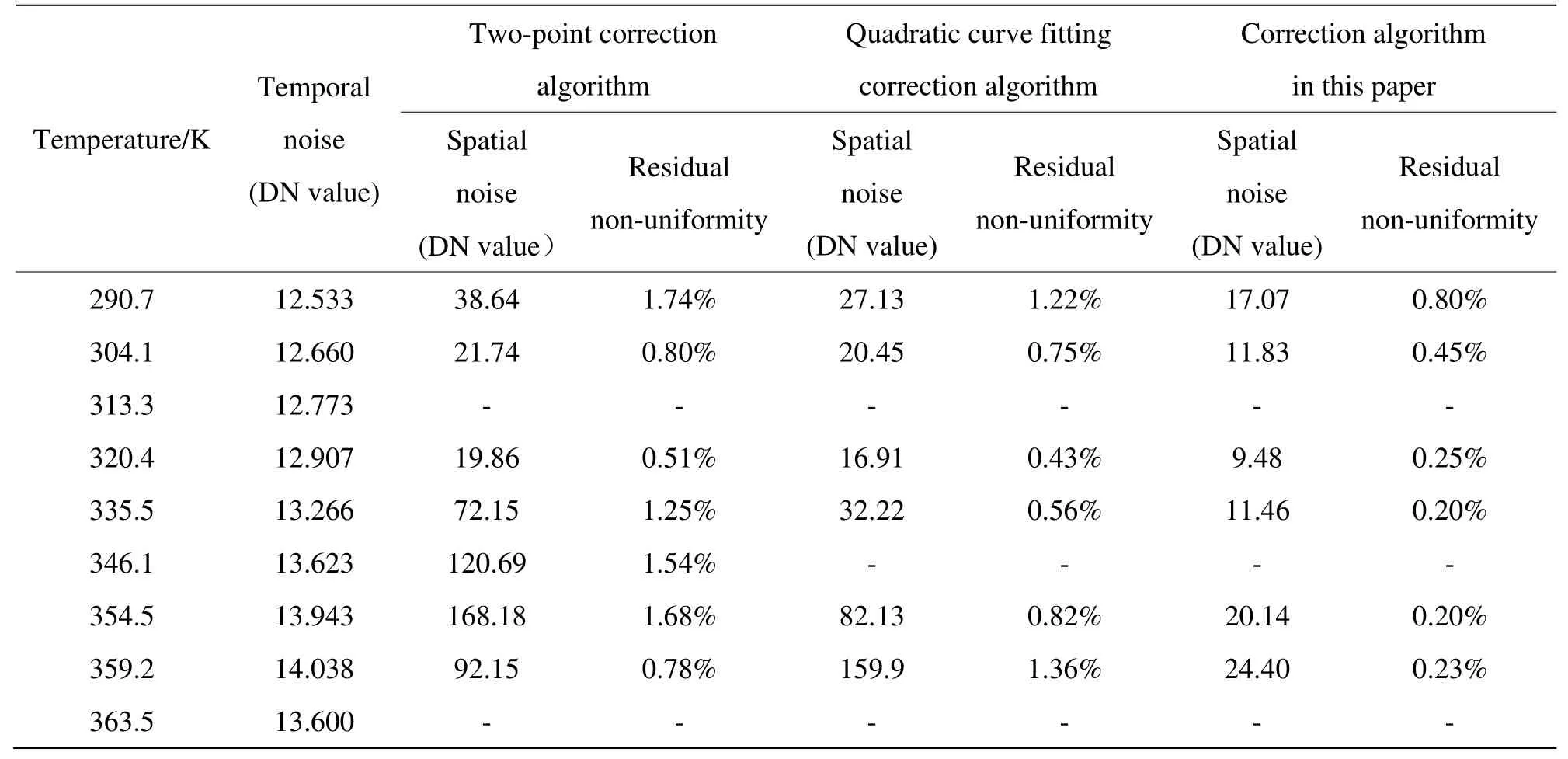
表1 不同算法校正前后图像质量比较Table1 Comparison of image quality before and after correction with different algorithms

表2 不同算法校正前后局部图像质量比较（320.4 K）Table2 Comparison of local image quality before and after correction with different algorithms(320.4 K)

图14 校正后不同通道两列像元二次拟合响应曲线分析Fig.14 Quadratic fitting response curve analysis of two columns of pixels in different channels after correction

图15 本文方法校正后黑体图像和直方图Fig.15 Black body image and histogram after correction by this paper

对比图2和图3可以看到，不论是两点校正法还是二次曲线拟合校正算法，最后得到的黑体图像都会呈现出比较明显的区域差异，相应的直方图分布也会出现比较大的跨度。而本文算法由于针对不同区域的响应特性分别进行校正，最终得到了预期的效果。

4 结论

由于大面阵探测器不同区域之间像元响应的差异性，传统的针对小面阵（面阵规模几百乘几百）的非均匀性校正算法对于大面阵红外探测器的校正效果较差。本文首先通过辐射定标和曲线拟合，分析出某大面阵红外探测器不同区域之间的响应特性，并以此为依据进行区域划分，然后分别对每个区域进行校正，最后通过校正偏置系数以及神经网络算法等方法校正区域间的不均匀性。实验证明，该算法校正效果良好，为后续红外成像的应用打下了坚实的基础。