基于航空公司的航班计划优化与延误预测

张舜尧， 戴福青

(中国民航大学空中交通管理学院， 天津 300300)

随着中国民航业的发展，航班数量快速增长。加上中国空域的特殊情况，导致航班延误频发。航空公司通过在航班串中投入软备份运力来抵消延误，保证航班正常率。如果软备份运力投入过少，航班衔接紧密，会导致不能有效消除延误，航班正常率达不到要求；软备份运力投入过多，又会造成飞机利用率低，影响航空公司效益。因此，如何在每个航段投放合理的软备份运力，提高航班鲁棒性的同时提高飞机利用率具有重要的意义。然而，航班延误具有突发性，天气、机场、机务等原因会破坏优化后的航班计划，造成航班延误。如果可以提前预知航班延误的发生，就可以提前做出反应，减少延误带来的损失。因此，预测航班延误同样具有重要的意义。

针对航班计划优化问题，中外学者从各个角度进行了研究。文献[1]通过构建波及延误树，研究延误传播过程，对航班过站时间进行重分配；文献[2]利用贝叶斯网络对航班过站时间动态估计；文献[3]找出航班串中的关键机场，对关键机场进行延误预测，并调整航班计划；文献[4]在考虑延误传播的基础上建立了航班延误计算模型；文献[5]提出了各种因素导致的波及延误及相关模型；文献[6]通过优化终端区航班到港排序，减少航班延误；文献[7]综合考虑了飞机路线和机组任务对航班延误的影响，通过调整过站时间来减少延误。而针对航班延误预测问题，中国几位学者在其他领域预测方面的研究具有参考价值。文献[8]采用加权马尔科夫链预测灌区年用水量；文献[9]采用传统的马尔科夫链对航空公司未来一周的航班延误进行预测；文献[10]根据误差平方和最小准则求解一步转移矩阵，利用马尔科夫链预测长江流域水质。

目前研究航班计划优化都是通过在航班过站时间中投放软备份运力来吸收延误，达到提高航班正常率的目的。但是，根据民航局新规，目前航班正常率的统计方法已经发生了改变。一个航班起飞时发生了起飞延误，只要实际到港时间不晚于预计到港时间，该航班就算作是一个正常航班。所以航空公司为了保证航班正常，通常会在飞行时间中加入软备份运力，达到准点到达的目的。因此，只研究航班过站时间中软备份运力的投放已经脱离了实际生产。

现针对航班飞行时间和过站时间中的软备份运力进行研究，根据航班延误的历史规律建立航班优化模型并求解。针对航班延误预测的研究，目前大多是通过马尔科夫链，利用一次转移矩阵预测后续延误。然而，航班延误具有突发性和较强的不可预测性，利用一次转移矩阵预测航班延误往往会较大得偏离实际情况。拟采用加权的马尔科夫链，以期能够更精确地预测到航班串中即将发生的延误，降低延误带来的损失。

1 研究的理论与模型的建立

1.1 相关概念

1.1.1 独立延误与波及延误

独立延误指的是由于天气、机务、流量控制等原因造成的延误，即延误是由该航班段自身原因产生的，与上游航班无关；波及延误指的是上游航班发生延误时，该延误传递到下游航班，造成下游航班发生延误，即延误是由上游航班引起的，与自身原因无关。

1.1.2 软备份运力及其作用

针对航班不正常事件频发的现状，民航局要求航空公司投入备份运力来缓解延误。备份运力分为硬备份和软备份两种。硬备份指航空公司拿出规定数量的飞机放在选定的机场作为备份运力。软备份以“备份可用运行时间”作为具体表现形式：①在飞机最少过站时间的基础上增加适量过站时间；②在民航局允许的范围内，在实际的飞行时间基础上增加一些时间，作为航班预计到达时间。

在飞行时间中的软备份运力可以抵消起飞延误，使部分晚起飞的航班准点到达，提高航班段的正常率；在过站时间中的软备份运力可以抵消到达延误，使部分晚到的航班不会影响到下一个航班的正常运行，提高下游航班的起飞准点率。

1.1.3 加权马尔科夫链的原理

马尔科夫过程是指随机过程中，在某一时刻状态已知的条件下，下一时刻所处的状态只和此时刻有关，而与以前时刻的状态和与未发生的状态都无关，则这种随机过程称为马尔科夫过程。而时间和状态都是离散的马尔科夫过程，又称为马尔科夫链。利用马尔科夫链预测的关键在于求出状态转移矩阵：从状态Ai(m)经过m步转移到状态Aj(m)的概率即为状态转移概率pij(m)，则状态转移概率矩阵为

(1)

P(m)反映了状态之间的移动规律。传统马尔科夫链通常会在得出一步转移矩阵P(1)之后，利用A(m)=A(0)P(1)m来预测系统未来的发展。然而，航班延误的发生具有突发性，采用传统马尔科夫链预测会产生很大的误差。因此，可考虑采用加权马尔科夫链。

(1)计算样本的自相关系数

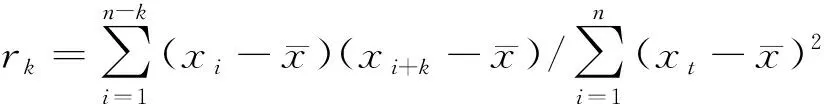
(2)

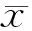
(2)计算各滞时马尔科夫链相关系数权重

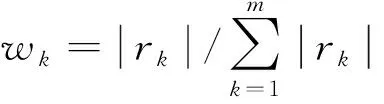
(3)

式(3)中：rk为式(2)计算所得的样本的自相关系数。

(3)预测n+1时刻所在的状态

(4)

1.2 航班计划优化模型建立

1.2.1 参数

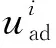
1.2.2 变量

xi,j表示在第i个航段第j个阶段投入的备份运力时间，j=1表示在飞行阶段，j=2表示在过站阶段。

1.2.3 模型建立

(5)

Ti,m+xi,2≥Ti,m

(6)

(7)

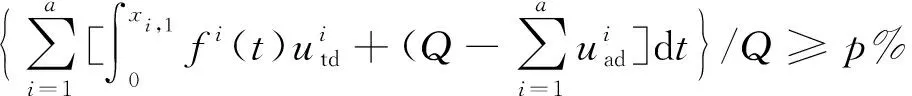
(8)

(9)

xi,j≥0且xi,j∈N

(10)

目标函数(5)是使优化后投入的备份运力最小；约束(6)保证了飞机在航班串的每一个过站机场都能满足最小过站时间的要求；约束(7)保证飞机的使用时间不超过最大可用时间的限制；约束(8)使航班串总体正常率即到达准点率能够达到p%；约束(9)使航班航班串总体起飞准点率能够达到q%；约束(10)是非负约束和整数约束。

2 实例分析

以航空公司B提供的一整个航季的航班数据作为研究资料，选取某一条延误较为严重的航班串(表1)，对经过3个机场的4个航班所构成的710个航班数据进行分析，研究软备份运力分配之后航班串正常率的变化；以及前序航班发生延误之后对后续航班的延误预测。

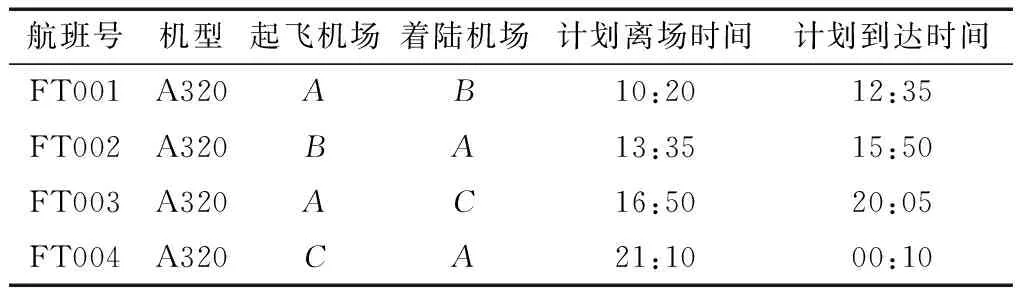
表1 案例学习航班串

2.1 软备份运力分配

2.1.1 航班延误数据拟合

利用MATLAB对航班串中每个航班段的起飞延误和着陆延误时间进行拟合，得到FT001航班延误时间的累积分布函数图像如图1所示，篇幅所限，其他几个航段的图像略。

图1 FT001延误数据拟合Fig.1 FT001 delay data fitting

FT001～FT004航段延误时间均服从负二项分布x～NB(r,p)，其概率密度函数为

f(v;r,p)=Pr(X=v)=

(11)

概率密度函数中r和p的拟合结果如表2所示。

表2 r、p的取值

由于FT004航班为尾航班，其延误不会传播到下一个航班，故只需研究其起飞延误即可。

2.1.2 模型中参数的确定

民航局规定的A320机型最少过站时间如表3所示。

表3 A320最少过站时间

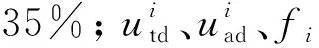
表4 模型中参数的取值

2.1.3 模型求解

通过MATLAB软件对航班计划优化模型进行求解，运行环境为 Intel Core i5-5200U CPU@ 2.2GHz处理器、8GB 内存、64 位 Windows10 操作系统，航班计划优化结果及对比如表5所示。

表5 航班计划优化结果

通过表5可知，在FT001航班的飞行时间中投入11 min的软备份运力，可以使到达准点率提高30.1%，在过站机场B投入10 min的软备份运力，可以使FT002航班的起飞准点率提高52.3%；在FT002航班的飞行时间中投入15 min的软备份运力，能使到达准点率提高40.3%；在FT003航班的飞行时间中投入7 min的备份运力，能使到达准点率提高33.5%，在过站机场C投入10 min的软备份运力，能使FT004航班的起飞准点率提高35.4%；在FT004航班的飞行时间中投入20 min的软备份运力，能使到达准点率提高14.7%。

最终通过优化，共增加73 min软备份运力，航班串的总体准点率达到了71.1%，比优化前提高了41.5%，优化效果明显。

2.2 基于加权马尔科夫链的航班延误预测

通过上一部分航班计划的优化，整个航班串的鲁棒性得到了很大的提升。然而，在发生航班延误之后，机场因素往往会加重延误。例如，AB航段发生了起飞延误40 min，通过上一部分的航班优化，可以使到达延误减小到29 min，BA航段的起飞延误减小到19 min。然而，如果此时过站机场B由于流控等原因处于延误状态，那么BA段的起飞延误会大于19 min，并把延误传递给后续航班。因此，对机场延误状态进行的预测，对于提高整体航班串的正常率有着极为重要的作用。

选取目标机场的航班延误率作为衡量机场航班延误状态的指标。航班延误率计算方式为：延误航段班次/计划航段班次，它用于衡量航班延误的次数与波及范围。采用样本均值-均方差分级法计算航班延误率的变化区间，即

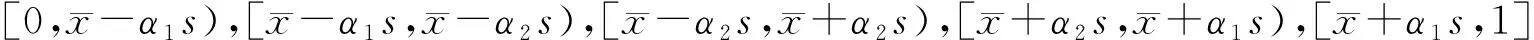
(12)

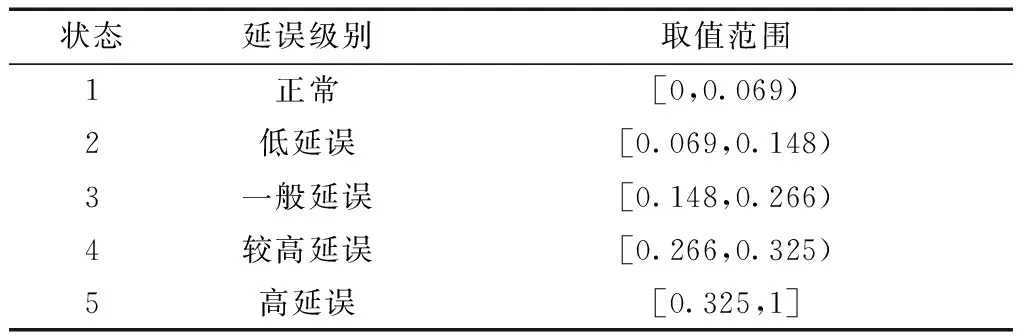
表6 航班延误分级标准

表7 机场A、机场B平均延误状态

由式(1)结合表7得出机场A、机场B的1～3阶状态转移矩阵为

由式(2)和式(3)得出机场A和机场B的1～3阶的自相关系数rk和权重wk，如表8所示。

表8 各阶自相关系数和各步长的马尔可夫链权重

由优化后的航班时刻表可知，航班FT001起飞机场为机场A，起飞时间10:20,处在时间序列6；航班FT002起飞机场为机场B，起飞时间13:51，处在时间序列7；航班FT003起飞机场为机场A，起飞时间17:21，处在时间序列9。因此，只需要预测处在时间序列6和9的机场A延误状态和处在时间序列7的机场B延误状态就能够得出FT001、FT002、FT003出港时机场的延误状态会对航班构成多大的影响。以FT003为例，由式(4)计算得到16:00—18：00时机场A的延误状态，如表9所示。

表9 机场A 16:00—18:00延误状态预测

max{pi}=0.498 8,此时i=2即机场A在16:00—18:00时处在低延误状态，对FT003航班离港的影响不会很大，只需要作出相应的预警即可。

3 结论

从航空公司的角度出发，构建了航班计划优化模型。将软备份运力分别投放在飞行时间和过站时间中，提高了航班的正常率、航班的起飞准点率和航班串的鲁棒性。通过追踪航班串中各航班的过站机场和离港时间，用加权马尔科夫链预测在该时间段过站机场的延误情况，判断机场因素是否会加重航班串的延误情况，并能够提前做出预警，进一步提高了航班串的鲁棒性。本文的不足之处在于航班计划优化模型考虑的约束条件还不够充分，并且优化仅针对单一的航班串，没有考虑多个航班串同时优化。