一种基于机器人操作系统的代价地图自适应膨胀半径设置方法
龚志力, 谷玉海*, 朱腾腾, 任 斌
(1.北京信息科技大学现代测控技术教育部重点实验室, 北京 100192;2.北京航天长征飞行器研究所, 北京 100076)
移动机器人自主导航技术作为各项高新技术综合应用的载体,在各个行业均展现了巨大的应用价值[1]。在移动机器人进行自主导航前,还需要依赖同步定位与建图(simultaneous localization and mapping,SLAM)技术完成机器人在未知环境中的地图构建。目前主要应用在移动机器人自主导航的地图类型主要分为拓扑地图[2]、栅格地图[3]和语义地图[4],三种方法各有其优劣和不同的适用范围。
其中栅格地图易于实现建模、更新与处理,具有结构简单、便于存储计算等优点,是目前移动机器人自主导航中研究和应用最广泛的地图类型。栅格地图把环境信息离散划分成一系列栅格,用概率值表征该栅格位置下的障碍信息。一般情况下只含简单的布尔信息,因此在复杂环境下寻求更优路径有一定局限性。为改善栅格地图的缺陷,李天成等[5]提出了一种极坐标下扇形栅格地图的建立方法,构建了一种新型高效的工作空间。岳伟韬等[6]提出了“有义地图率”的表征栅格地图准确度的概念,提供了以准确度和信息量评估栅格地图获得最佳栅格大小方法。余文凯等[7]基于K-means聚类算法对栅格地图进行分区并提出了量化各局部区域的复杂度的方法。张福海等[8]改善代价地图与室内环境的匹配性,提升了地图更新的速度。
以上研究成果均针对传统栅格地图建立方式进行优化,使栅格地图能包含更多环境信息,以提高自主导航效率。在移动机器人导航中对栅格地图的优化由代价地图完成。代价地图对传统栅格划分新的区域,根据传感器数据实时更新障碍物信息,机器人移动时在障碍物周围设置一层安全缓冲区。相比于其他种类地图,代价地图更有助于机器人的定位与导航[9]。如今随着移动机器人自主导航应用范围的不断扩大,代价地图也逐渐表露出了应对复杂环境时障碍物划分不灵活、路径规划不理想等不足。
现提出一种基于机器人操作系统(robot operating system, ROS)的代价地图自适应膨胀半径设置方法及一种改进A*路径规划算法,优化移动机器人自主导航中的地图构建与路径规划,以提升移动机器人自主导航过程中应对复杂环境的安全性和鲁棒性。
1 代价地图构建
获取地图信息是ROS移动机器人进行自主导航的第一步。代价地图是由机器人接受各类传感器采集到的环境数据而创建、更新的二维或三维地图。通常情况下ROS中的代价地图采用栅格形式,根据与障碍物的碰撞情况可以分为三种状态:无障碍(Free)、有障碍(Occupied)和未知区域(Unknown)[10]。
1.1 代价地图的分层
代价地图由多个层组成,每个地图层(Layer)都有其特定的功能,各个地图层的信息叠加生成最终的代价地图信息。如图1所示,静态地图层(Static Layer)是第一层,障碍物层(Obstacle Layer)是第二层,膨胀层(Inflation Layer)是第三层。这三层组合成了叠加各个地图层后的代价地图(Master map),为路径规划模块提供地图信息。
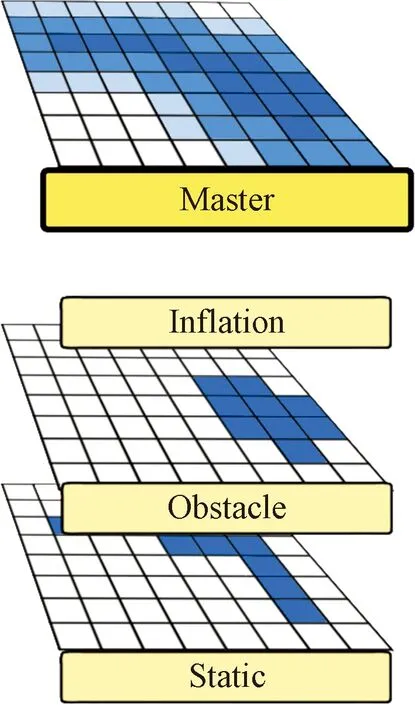
图1 Master map及基础地图层Fig.1 Master map and basic layers
1.2 代价地图的更新
代价地图以一定的周期进行更新,每个周期中都要依据更新的传感器数据对代价地图底层结构进行标记(mark)和清除(clear)操作,再将各层信息投影到master map上得到相应的代价值。mark操作将地图上障碍物坐标对应的栅格设置为致命代价值,clear操作将清除雷达向外发射线穿过栅格的代价值设置为无障碍[11]。如存储的障碍物信息为3D,则需要将每一列障碍物信息投影成2D后才能放入代价地图中。
更新过程主要分为两个阶段:阶段一为各个Layer的更新,阶段二为Master map的更新。阶段一中,拥有自身实体地图信息的地图层会更新从传感器获得的新增区域的代价值,如Static Layer和Obstacle Layer;自身不维护地图的地图层则不会更新,如Inflation Layer。阶段二中,会将各个地图层的数据逐一添加至Master map。
1.3 代价地图栅格概率值
代价地图中的一个栅格在计算机内存中占用一个字节,可以表示0~255中的任意数字,称为栅格代价值。根据Bresenham算法对障碍物点进行标记[12],填充机器人传感器位置到障碍物之间的栅格概率。获得障碍点的坐标后,需要对障碍点做膨胀处理,即根据栅格代价值函数填充障碍物周围膨胀区栅格的代价值。
令一栅格qn到距离它最短欧式距离的障碍点的距离为d(qn),栅格qn的栅格代价值记为c(qn),其栅格代价值函数为
c(qn)=
(1)
式(1)中:ra为每个栅格的边长;ri为机器人地面投影轮廓的内切圆半径;rc为外接圆半径;rm为人为规定的代价地图膨胀半径;w为代价值下降权重。由式(1)可得如图2的栅格代价值分布示意图。

center cell为机器人轮廓几何中心栅格
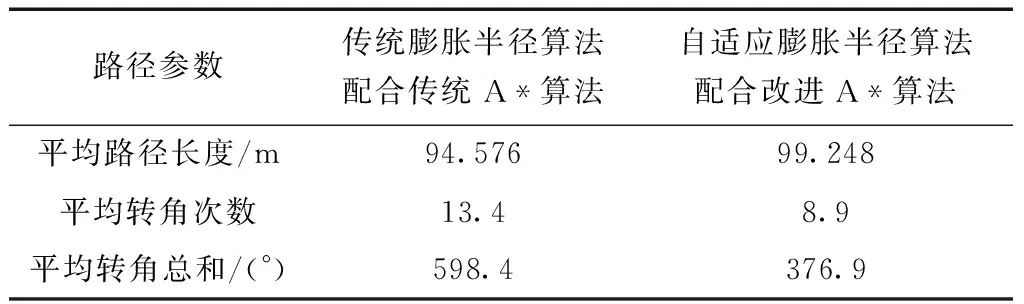
若ra≤d(qn) 若ri≤d(qn) 若ri≤d(qn) 若rm≤d(qn),珊格代价记为自由空间(Free space),属于没有障碍物的空间。 据式(1)可知,在对障碍物膨胀处理中,膨胀半径为定值,选择的膨胀半径是否合适在一定程度上决定了避障效果的好坏。 在室内环境中,利用目前较为成熟的SLAM算法如gmapping,cartographer等能实现较好的导航效果[14]。但在室外环境处于非结构化环境中的密集障碍物群时,代价地图中膨胀半径设置过大会阻碍局部路径规划,导致不能灵活地通过障碍物群而被困在障碍物之中。膨胀半径设置过小则会导致规划出与障碍物距离过近的危险路径,增大碰撞的风险。由此,根据机器人与障碍物的距离,提出一种代价地图自适应膨胀半径的设置方法。 设栅格地图分辨率为Δ,机器人与任一栅格的距离l转换成栅格距离d的计算公式为 (2) (3) 每次栅格地图更新时记录距机器人最远障碍点的距离Dmax,则可计算On的衰减系数coef。 (4) 结合式(1)可得到距离自适应膨胀半径栅格代价值函数s(qn)为 s(qn)= 代价地图对障碍物边缘的膨胀是栅格地图上的障碍点依据与机器人的栅格距离,对其子节点迭代填充代价值的过程。 如图3所示,首先把某一障碍点On作为父节点,计算子节点(O1、O2、O3、O4)与On的距离d(qn),然后由d(qn)计算子节点的代价值。最后判断d(qn) 图3 迭代节点关系图Fig.3 Iteration node diagram 算法步骤如下。 (1)构造膨胀点优先队列inflation cells,将所有障碍点依次放入队列中,得到Dmax。 (3)判断d(qn) (4)由s(qn)计算出当前节点的代价值,与原始代价值比较,取最大值。 (5)从队列inflation cells中移除当前节点,返回步骤(2)。 为提高机器人的灵活性,在距离自适应膨胀半径算法基础上,针对机器人紧贴障碍物边缘行驶的情况,提出一种根据轮廓位置自适应调整膨胀半径的方法:在未紧贴障碍物行驶时保留更多的安全行驶空间,在紧贴障碍物行驶时再给出最低限度安全行驶空间。 如图4所示,七宫格为一个7行7列的平面方阵。算法开始时,把当前子栅格放入七宫格的中心位置[15],即第4行第4列,记为Pn,然后以这一点为中心,检测其余栅格的概率值。 图4 七宫格法Fig.4 Seven-grid method 无人车靠近某个障碍物点Pn时,周围非占据的栅格数量减少,被占据栅格数量增加。记nF为栅格值为FREE SPACE的栅格数量,nL为栅格值为LETHAL OBSTACLE的栅格数量。则可计算衰减因子sp。 (6) 结合式(5)得到自适应膨胀半径栅格代价值计算函数f(qn)。 f(qn)= (7) 计算步骤如下。 (1)在第2.1节步骤(2)的基础上判断当前处理节点是否为障碍点,如果是,则将其作为七宫格的中心;如不符合,则继承其On的衰减系数sp,进行步骤(4)。 (2)依次得到七宫格中的其余48个栅格值,累计得出值为FREE SPACE的栅格数量nF和值为LETHAL OBSTACLE的栅格数量nL。 (3)计算衰减因子sp,并将其继承到所有子节点。 (4)继续进行第2.1节中的步骤(3)。 为实现本文自适应膨胀半径算法,在Gazebo中搭建仿真环境,改写ROS中代价地图功能包进行测试。采用ROS Navigation导航框架,使用的SLAM算法为gmapping,不使用静态地图,在未知环境中进行实时建图导航。全局规划算法选取经典的A*算法,局部规划算法选取动态窗口法(dynamic window approach,DWA)。在相同的障碍物分布情况下对比膨胀半径设置效果以及路径规划情况。所使用的程序运行在Ubuntu18.04操作系统中,运行内存为8 GB,主频为2.3 GHz,ROS版本为Melodic。 Gazebo中自适应膨胀半径设置方法使用前后效果如图5所示。 图5 自适应膨胀半径方法效果对比Fig.5 Comparison of effect of adaptive inflation radius Gazebo下设置单一障碍物情景,相同起始点和目标点下使用膨胀半径算法的路径导航效果如图6所示。 图6 Gazebo中简单情境导航效果对比Fig.6 Comparison of the effects of simple situation navigation in Gazebo Gazebo下设置复杂障碍物情景,相同起始点和目标点下使用膨胀半径算法的路径导航效果如图7所示。 图7 Gazebo中复杂情境导航效果对比Fig.7 Comparison of the effects of complex situation navigation in Gazebo 仿真结果表明,障碍物的膨胀半径随与机器人的距离远近而自适应的调整大小,证明了自适应膨胀半径算法的有效性。机器人紧靠障碍物行驶时,机器人在保证安全的前提下能预留出更多的局部规划空间。复杂障碍物情景下,使用传统的膨胀半径算法,全局规划路径从障碍物之中穿过,最终机器人进入障碍物群中,与障碍物发生碰撞被困,导航失败;使用改进后的膨胀半径算法,机器人在遇到复杂障碍物情况时,全局路径规划成功绕过障碍物进行导航,最终到达目标点,导航成功。 结合代价地图自适应膨胀半径算法,设计了A*路径规划算法的估价函数f(n),根据环境信息设置动态衡量启发函数,在无障碍物环境适当提高搜索效率。对子节点的选择进行进一步优化,避免路径通过障碍物顶点。 A*算法是一种启发式搜索算法,结合了Dijkstra和广度优先搜索(breadth first search,BFS)两种算法的优势[16],在搜索效率和搜索广度做到平衡。算法中以距离值表征路径代价。其代价函数f(n)计算公式为 f(n)=g(n)+h(n) (8) 式(8)中:g(n)为起始点到当前节点n实际路程的代价函数,由累计当前节点与父节点距离值得到;h(n)为当前节点到目标点的估计路程代价的启发函数,通常使用当前节点与目标点的曼哈顿距离或欧式距离,此算法采用欧式距离。针对自适应膨胀半径方法使得机器人避开复杂环境的情况,结合环境信息对启发函数设置了权重函数w(n),公式为 (9) (10) 式中:ds为当前节点与起始点的距离;dg为当前节点与目标点的距离;t为同级子节点中障碍节点的数量。 由式(10)可知,权重函数w(n)∈[1,e]。在无障碍物环境中,随接近目标点的过程,启发函数权重逐渐增大,提高了搜索效率。 传统A*算法在栅格地图上选择子节点时,欠缺了对路径与障碍物位置关系的考虑,使得部分路径穿过障碍物顶点,增大了发生碰撞的风险[8]。针对这一问题对子节点的选择条件进行优化,提高路径规划的安全性。 子节点和父节点的位置关系如图8所示,将处在顶点位置上的4个节点归为危险子节点(子节点1、3、5、7)。 图8 节点位置关系图Fig.8 Node location relationship diagram 在选子节点时,若该子节点为危险子节点,则检测其临近的两个子节点是否存在障碍节点,若存在则放弃该危险子节点,若不存在则将其作为子节点。 优化子节点选择条件后,解决规划后的路径穿过障碍物顶点的问题,避免机器人在运动过程中与障碍物发生碰撞。 在MATLAB中建立60×60大小的栅格地图作为移动机器人工作环境,将自适应膨胀半径算法配合改进A*算法与传统膨胀半径算法配合传统A*算法进行对比仿真测试。 为方便此次对比实验,设定移动机器人的工作环境栅格边长为单位1 m,设传统膨胀半径设置方法的膨胀半径为2 m,最低限度安全行驶半径为1 m。 栅格中左下角为起点,右上角为目标点。黑色网格为障碍物,蓝色网格为障碍物膨胀区域。模拟密集障碍物分布,随机改变障碍物位置进行6组对照实验。其中一组传统膨胀半径算法配合传统A*算法路径规划效果如图9所示,自适应膨胀半径算法配合改进A*算法路径规划效果如图10所示。使用两种算法的平均实验路径参数如表1所示。 图9 传统膨膨胀半径算法配合传统A*算法路径规划Fig.9 Conventional inflation map algorithm combined with traditional A* algorithm 图10 自适应膨胀半径算法配合改进A*算法路径规划Fig.10 Adaptive expansion radius algorithm and improved A* algorithm path planning 表1 实验路径参数表Table 1 Experimental path parameters 由表1数据可知,6组对照实验中,相比于传统算法,使用自适应膨胀半径算法配合改进A*算法后能避开密集障碍物群,转向次数和转角总和减少,路径不再穿过障碍物顶点。由于需要避免进入密集障碍物群,平均路程增加4.9%。转向次数和总和分别减少33.6%和37%。 实验表明,结合自适应膨胀半径算法和改进A*算法规划后的路径,牺牲小部分最短路径,避开了密集障碍物群,在路径长度相差不大的情况下,转角次数和总和减少,根据环境信息不同提升了搜索效率。路径规划更平滑,路径通过的障碍物密度下降,易于机器人行驶通过。 通过对基于ROS的代价地图和A*路径规划算法研究,得到以下结论。 (1)提出一种代价地图自适应膨胀半径设置方法,可用于移动机器人全局路径规划时避开复杂障碍物群,局部规划时增加可行驶空间。 (2)提出一种改进A*路径规划算法,用于移动机器人导航全局规划,增加搜索效率,平滑路径,降低碰撞风险。 (3)改写ROS中代价地图功能包,在Gazebo仿真平台上对自适应膨胀半径算法进行导航测试,证明能避开复杂障碍物群。在MATLAB中对自适应膨胀算法配合改进A*算法进行验证。通过实验数据,证明该方法能提升机器人在复杂环境中导航的安全性和鲁棒性。 (4)自适应膨胀半径算法计算衰减系数增加了一定空间复杂度,导航安全较高的路径增加了部分路程长度。存在权衡上的不足需在未来做进一步研究。2 自适应膨胀半径算法
2.1 距离自适应膨胀半径算法
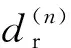
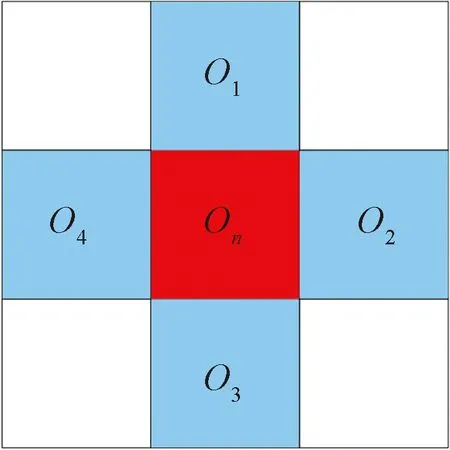
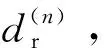
2.2 轮廓自适应膨胀半径算法

2.3 ROS导航中的应用效果

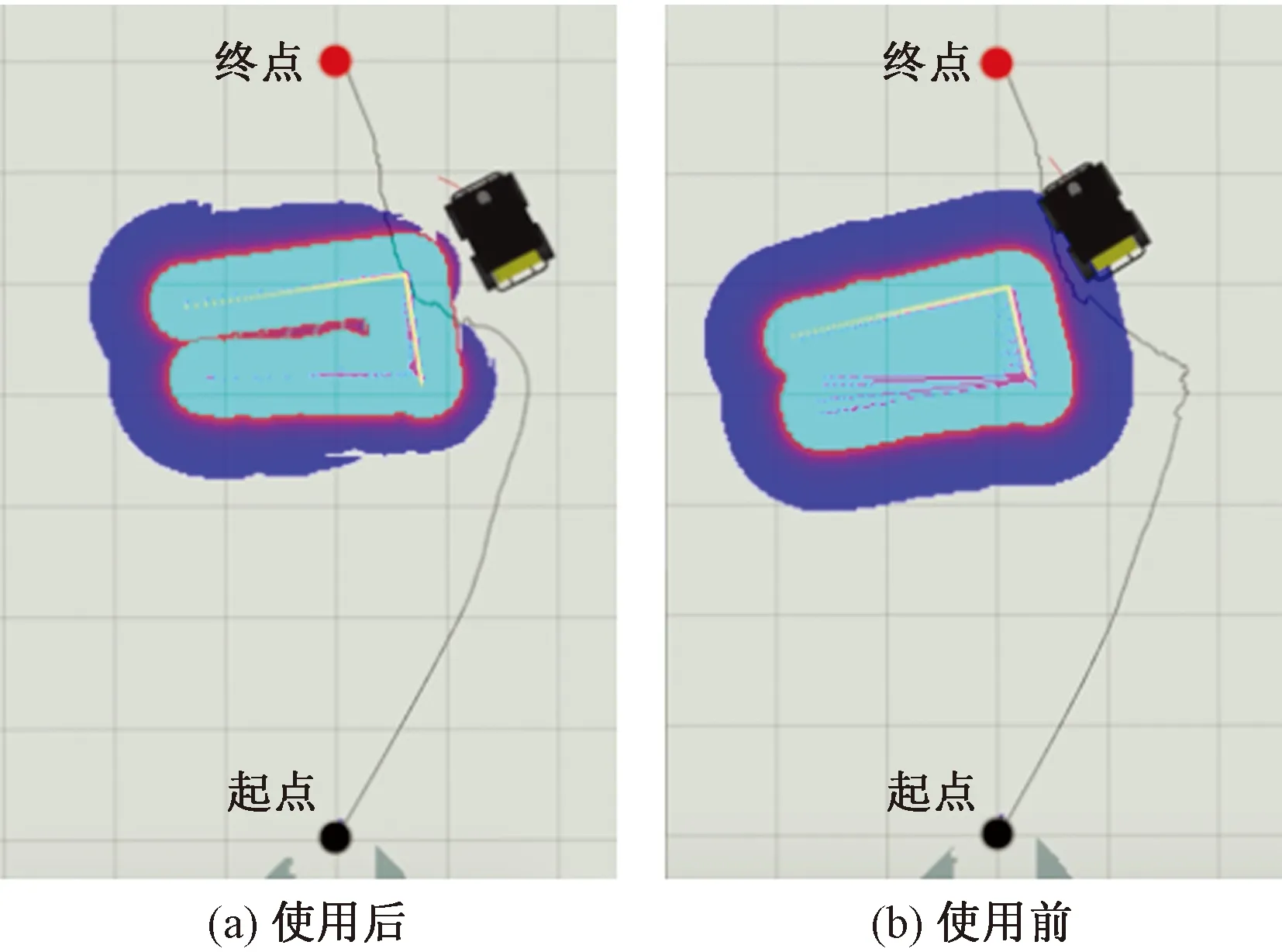
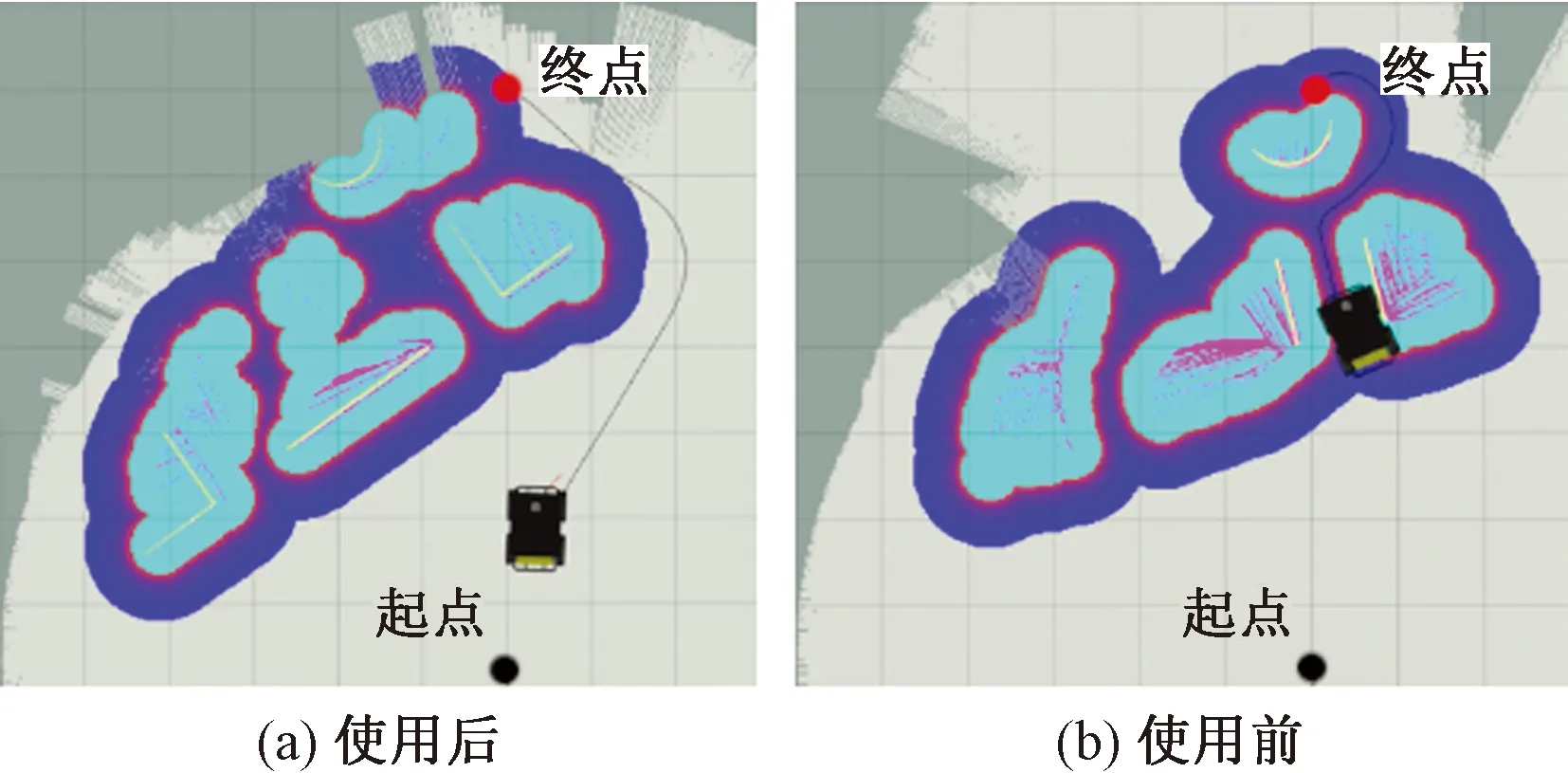
3 结合环境信息的改进A*算法
3.1 动态衡量启发函数

3.2 子节点选择的优化
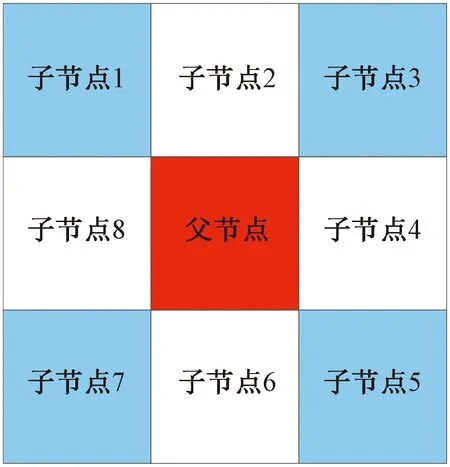
4 仿真实验与结果分析
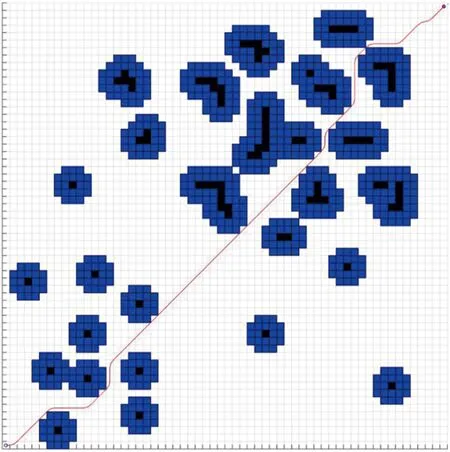

5 结论

