降雨条件下滚石斜坡失稳机理试验研究

叶唐进， 刘依缘， 王泽文， 李俊杰， 李 艳

(1.大连理工大学建设工程学部， 大连 116024； 2.西藏大学工学院， 拉萨 850000)

川藏公路西藏境内斜坡地质灾害极为发育，尤其是以冲洪积物为主的滚石斜坡，在降雨融雪、地震以及人为活动等条件下极易失稳，对公路安全及畅通造成了极大威胁。滚石斜坡是指以冲洪积层为主的高原河谷阶地，由于公路工程建设或河水冲刷等导致斜坡岩土颗粒裸露，在特殊的环境和气候作用下，其岩土颗粒不断滚落和滑动的一种碎屑斜坡，属于青藏高原河谷路段特有的地质灾害。通过野外调查统计，国道G318巴塘至拉萨的峡谷地段，由于公路工程建设和河水冲刷等因素形成了具有一定规模的滚石灾害64处，严重威胁过往行人及车辆的安全。因此，滚石斜坡在降雨条件下失稳的机理研究对公路沿线的滚石斜坡稳定性评价和有效治理具有十分重要的作用。

针对类似滚石斜坡的研究，起始于20世纪60～70年代，Ritchie[1]在岩石崩落评价及其防治中提出，岩崩是造成现代公路损坏的极其重要的因素，必须要加以控制；Peckover等[2]给出了一些简单的处理和预防崩落方法，但并不全面；Bozzolo等[3]开发了一个计算机模型用来模拟滚石运动轨迹与边坡地质条件的关系，得出滚石形成危险区的范围。杨志法等[4]将边坡的滚石机理、防治措施作为值得关注的地质力学问题提出；叶唐进等[5]结合野外调查、数值模拟初步分析了滚石斜坡的形成和失稳主要因素；郑光等[6]通过碎屑流室内滑槽试验和实例分析，研究了碎屑流的堆积特征及机理。近30年来人们研究滚石斜坡与其他斜坡的研究方法基本类似，主要集中在滚石斜坡的发育特征、物理力学性质、稳定性以及滚石砸中行人和车辆的概率[7]，但并未对滚石斜坡进行严格的定义和分类。

针对坡体的降雨模型试验主要集中在研究泥石流和滑坡，Chen[8]研究表明，降雨量是导致滑坡的重要因素，地势越高，越容易发生滑坡；Deng等[9]通过研究青藏高原东南部冰原泥石流，得出气温和降雨是产生泥石流的主要因素；李焕强等[10]通过对不同坡角边坡模型进行人工模拟降雨试验，实时监测坡体前端水平推力、坡体变形、坡体含水率3个方面指标，得到各指标在降雨入渗作用下变化规律；詹良通等[11]在人工降雨条件下进行了原位边坡模型试验，监测到非饱和膨胀土的原位数据；李静等[12]采用模型试验，在室内模拟降雨，探究降雨强度对碎石土边坡稳定性的影响，得出降雨时坡体入渗规律是自上而下逐渐渗透，含水率会随着降雨时长逐渐稳定的结论；倪凯军等[13]通过降雨入渗的室内边坡试验，模拟了降雨过程中雨水在边坡中的入渗过程及运移规律；甘建军等[14]通过室内固定式双渗透降雨物理模型试验，探究降雨入渗对不同坡度含软弱夹层堆积体边坡稳定性的影响，得到了孔隙水压力降雨停止后的滞后效应与坡度呈负相关。虽然此类试验方法数据真实，效果较为显著，但未见针对滚石坡在野外进行相应的模型降雨试验。

由于滚石斜坡仅在青藏高原存在，研究文献较少，且定义和分类都不太明确，同时研究主要集中在野外调查、数值模拟以及致灾概率分析，导致滚石斜坡的失稳机理不明，治理不彻底。通过野外滚石斜坡的调查和长期观测，发现降雨对滚石斜坡体的破坏具有十分明显的影响。因此，通过1∶1降雨模型试验，探究滚石斜坡在降雨条件下的失稳机理，并推导其降雨条件下稳定性计算的简布法公式。

1 模型试验

1.1 坡体几何特征

滚石坡主要分布于尼洋河谷阶地，以及怒江、澜沧江、金沙江及支流的河谷阶地，其主要成分为冲洪积物的卵石、砾石等，具有较高的磨圆度。滚石坡具有形成区和堆积区两部分，其失稳方式分为岩土颗粒滚落和局部滑动两类，如图1所示。

图1 野外滚石斜坡失稳及工程治理Fig.1 Instability and treatment of rolling stone slope

野外调查统计数据表明，野外滚石斜坡开挖的边坡坡度在35°～75°，坡体的上部分坡度在33°～36°。因此，试验的滚石斜坡在原有坡度35°的基础上，采用人工开挖，改变坡体下半部分的坡度，使其坡体下部分坡度以75°(1号坡)、55°(2号坡)、35°(3号坡)分为3组，每组3个斜坡，如图2所示，为坡体下部坡度75°和55°的斜坡。考虑其降雨范围，为避免坡面积水影响试验结果，在坡体两侧1.5 m处，开挖两条排水通道，利于排水。

1.2 坡体岩土参数

为使试验结果更精确，试验前对斜坡的相关参数进行了采样和测试，分别获取了样品的密度、颗粒级配、含水率、渗透性系数、黏聚力和内摩擦角等参数。

对3组斜坡进行采样，在室内进行筛分称量，测得3组试验坡体的颗粒级配如图3所示。从图3可知，滚石斜坡的主要成分为沙和砾石、卵石。

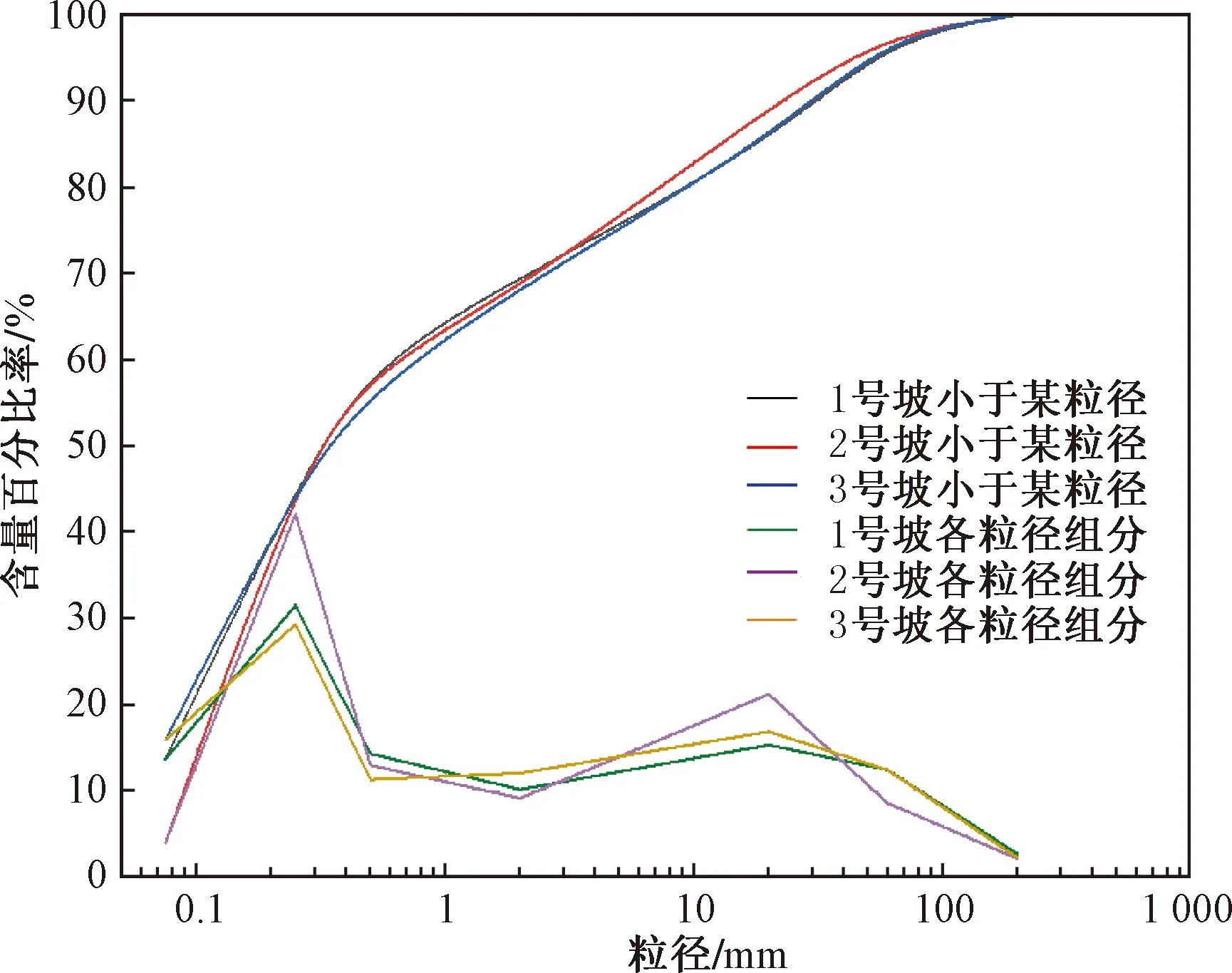
图3 试验坡体颗粒级配Fig.3 Experimental slope particle grading

通过现场测试和室内测试，得出斜坡的密度为1 347.8～1 593.3 kg/m3，含水率为4.74%～13.84%。对其力学性质和渗透性进行测试，得到其内摩擦角为34.9°～36.2°，黏聚力为0.10～0.14 kPa，渗透系数为2.993×10-2～3.966×10-2cm/s。

1.3 试验装置及斜坡特征

试验装置由人工模拟降雨系统、数据采集与分析系统[15]以及自然滚石斜坡3个部分组成。

人工模拟降雨系统由供水部分、控制调节部分以及降雨部分组成，如图4所示。其供水部分由水池、水泵和回流管构成，主要用于提供水源、动力和收集回流水。控制调节部分由水阀、压力表、水表及管件组成，主要用于控制降雨量、降雨强度。降雨部分包括输水伸缩管及连接件、移动卡口、移动横杆、可调喷头和伸缩支架，可调节降雨范围、降雨高度以及降雨方式等。

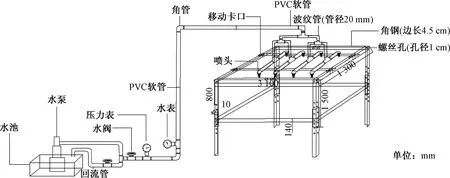
图4 人工模拟降雨装置Fig.4 Artificial rainfall simulator

数据采集系统由测量含水率、孔隙水压力、土压力及雨量的仪器组成。坡体孔隙水压力采用DMKY微型孔隙水压力计测量，YE2538仪来采集数据；利用RS-485土壤水分湿度传感器测量坡体土壤含水率；采用HRE-1土压力计和VW-102B振弦式读数仪来测量和收集土压力数据；采用自动读数雨量器采集降雨量及降雨强度。通过测试，几种传感器均满足本次降雨试验的精度要求。

1.4 试验准备与调试

首先需在野外找到类似的滚石斜坡，并对斜坡下部坡度进行人工处理，保证其坡度分别为75°、55°、35°，然后在图5中4#、5#、6#位置钻取1.5 m的感应探头安放孔。

在设备安装之前，需对所有设备进行测试和检查，确保所安装设备正常运行且误差在允许范围内。首先安装斜坡上的感应探头，并将感应探头与数据采集和控制中心连接，如图6所示。仪器埋置情况如图7所示，在A、B、C3个位置按照每隔50 cm的深度安装含水率、孔隙水压力和土压力探头，一共安装3组。其中A、B、C位置分别为图5中的4#、5#、6#位置，再次对所埋设感应探头进行逐一检测和校正。

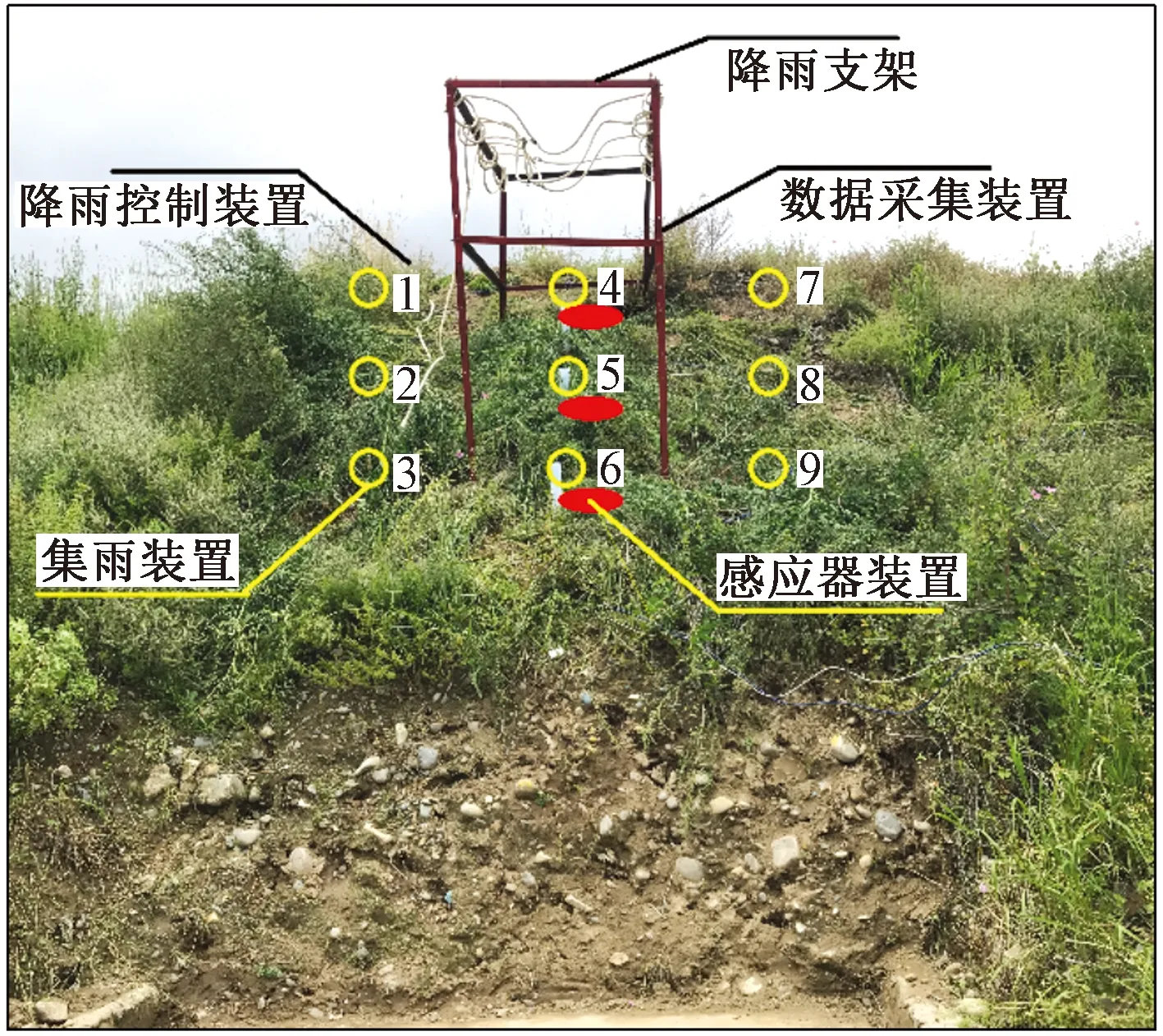
图5 斜坡上仪器安装图Fig.5 Photo of instrument installation on slope

图6 数据采集和控制中心Fig.6 Data acquisition and control center

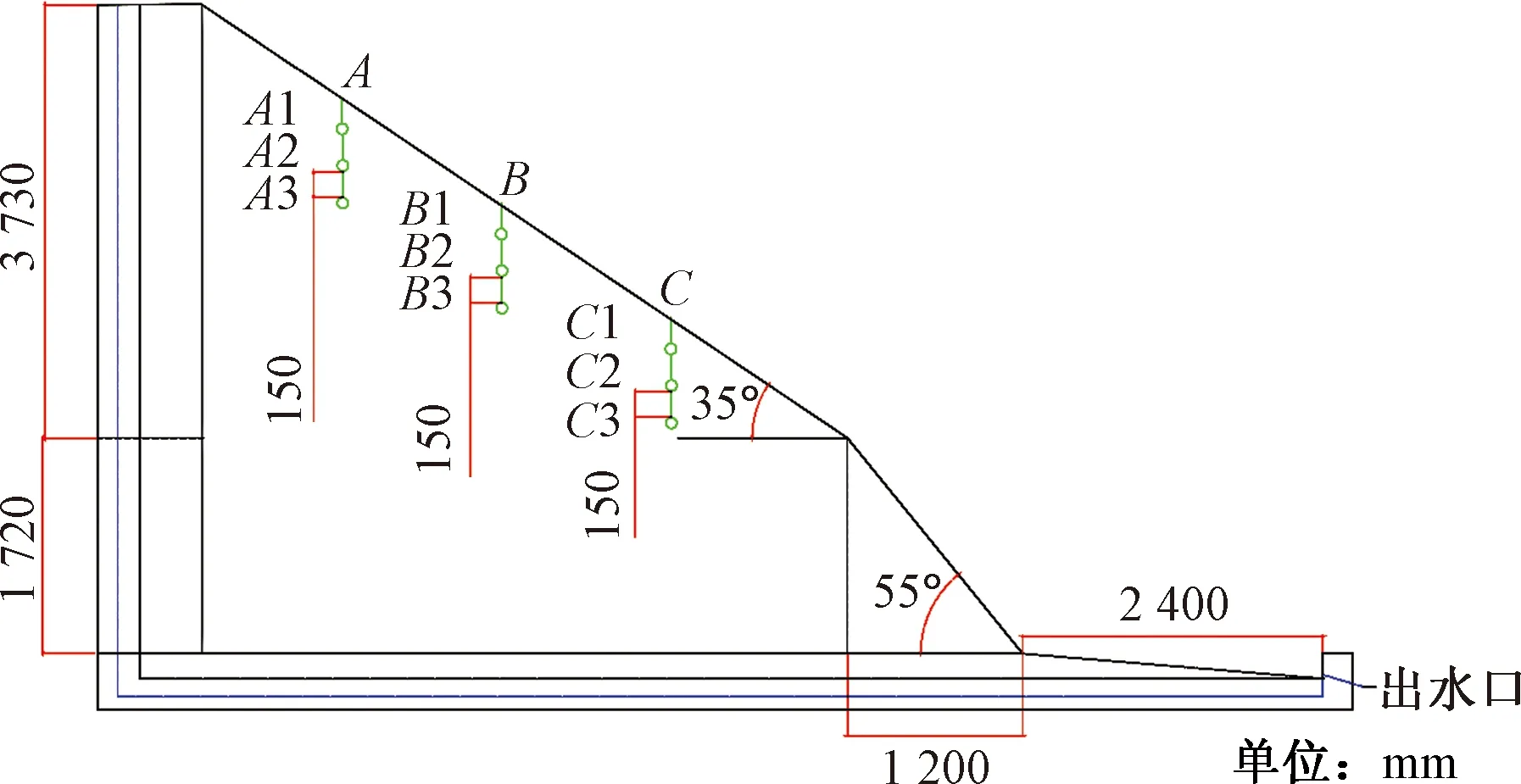
图7 仪器埋置设计Fig.7 Instrument embedment design drawing

根据试验方案准备的降雨强度、降雨量、降雨时长等关系调节降雨系统，安装调试雨量器和各感应探头，检查电源和摄像系统，然后测量初始的孔隙水压力、土压力及含水率数值并记录，打开摄像仪器和降雨系统开始试验。按照降雨时长安排关闭降雨系统，考虑斜坡破坏的滞后效应，感应探头需在降雨结束后继续工作2 h。

1.5 试验结果分析

1.5.1 颗粒失稳及破坏过程

从降雨试验的岩土颗粒失稳来看，降雨开始的1′19″，斜坡高2.1 m处出现第1颗滚石，堆积于斜坡前端平台0.23 m处，一直到32′18″为止，岩土颗粒不断滚落，均从1.5～2.2 m的蓝色区域滚落，滚落的顺序及位置如图8(c)所示，当斜坡出现坡面洪流时，再没有出现岩土颗粒滚落，说明岩土颗粒的滚落发生在降雨至斜坡表面的坡面洪流期间。

图8 滚石斜坡失稳方式与运动过程Fig.8 Instability mode and movement process of rolling rock slope

从图8(d)的48′11″开始，在斜坡的左下角坡体较为松软部位开始出现小的局部滑动，一直到图8(h)的89′55″，斜坡局部一共滑动了5次，且每次均比前一次规模要大。在图8(h)的89′55″处，斜坡顶部出现了大量的拉张裂缝，如果降雨持续下去，将导致滚石斜坡的整体失稳下滑。分析其原因为降雨导致滚石斜坡表面岩土颗粒黏聚力和内摩擦角减小，岩土颗粒不断滚落下滑。

1.5.2 斜坡局部滑动

从试验现象和图8可得出，滚石斜坡的破坏分为岩土颗粒失稳和局部滑动破坏，现对局部滑动进行分析。为了便于对比分析，将3组斜坡试验感应探头进行编号，如表1所示。由于A2、A3、C2、C3 4个位置探头数据意义不大，在此不列出比较。

表1 感应探头编号Table 1 Inductive probe number

1.5.3 含水率、孔隙水压力和土压力分析

(1)含水率变化规律。由图9可知，开始降雨后，3组坡体0.5 m埋深含水率首先增加并达到饱和，然后依次是1 m埋深、1.5 m埋深；在持续降雨1.9 h时，55°坡体发生滑动，使其7#、8#和10#含水率均出现下滑，其中10#含水率由34%下降至4%；75°和35°斜坡含水率一直都小于55°斜坡的含水率，且没出现滑动。试验表明，斜坡较陡或较缓都不利于降雨入渗，含水率难以到达饱和值，不易失稳下滑；而当斜坡在55°时，利于降雨入渗，极易使斜坡含水率达到饱和，从而导致斜坡失稳滑动。

图9 含水率变化曲线Fig.9 Change curve of water content

(2)土压力变化规律。由图10可知，土压力与含水率变化规律具有相似之处，受含水率影响，55°斜坡的土压力最大，在1.9 h处发生下降，斜坡失稳滑动，7#、8#和10#的土压力同时出现下降，而75°和35°土压力曲线变化较小。说明降雨入渗，导致斜坡土压力增大，斜坡失稳下滑。

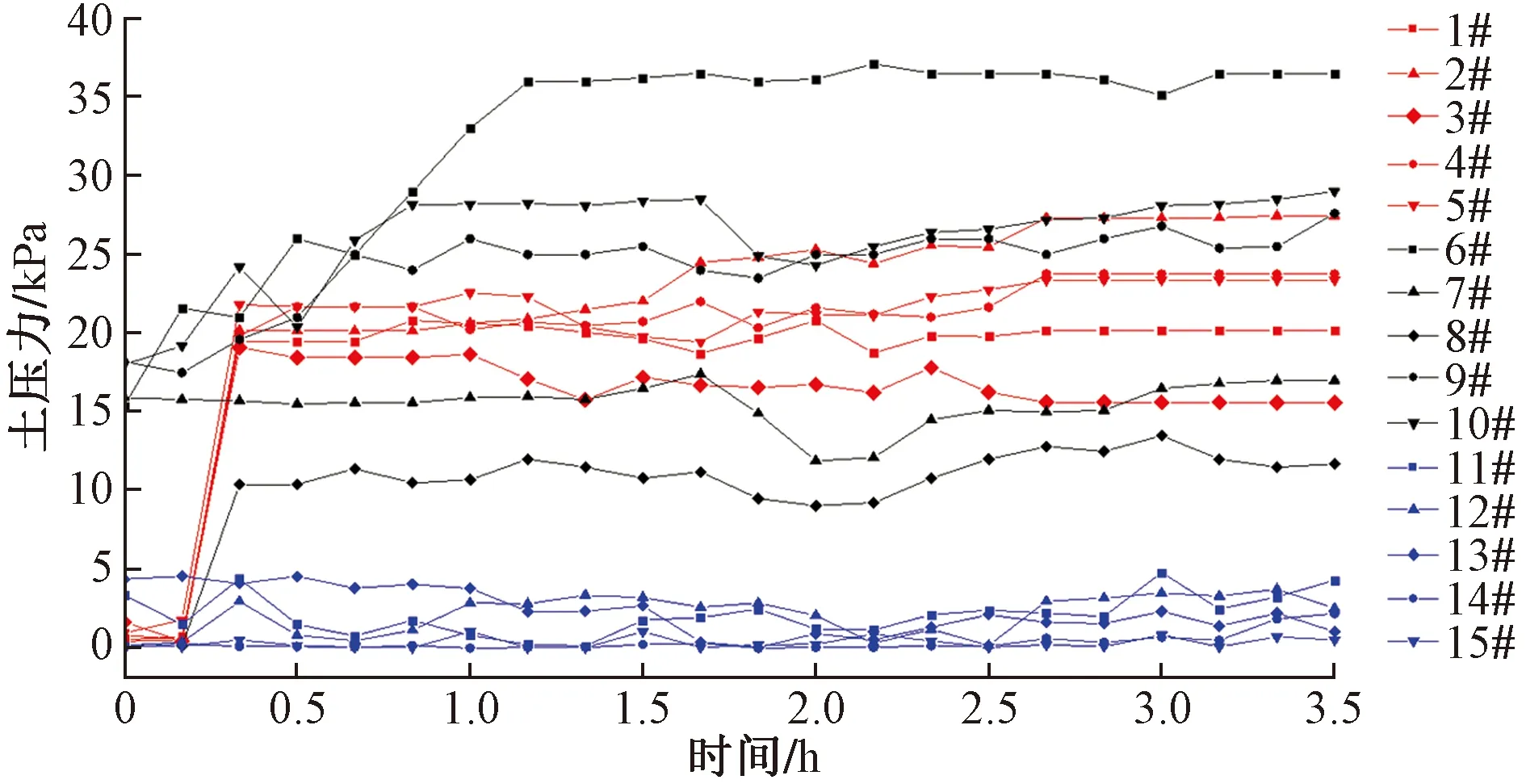
图10 土压力变化曲线Fig.10 Change curve of earth pressure

(3)孔隙水压力变化规律。由图11可知，由于孔隙水压力极为敏感，且单位较小，其曲线出现小小的起伏，但整体规律还是与含水率及土压力变化一致。55°斜坡的孔隙水压力仍然是最大的，且在斜坡失稳下滑时孔隙水压力也急剧降低。而75°和35°斜坡孔隙水压力变化不太明显。

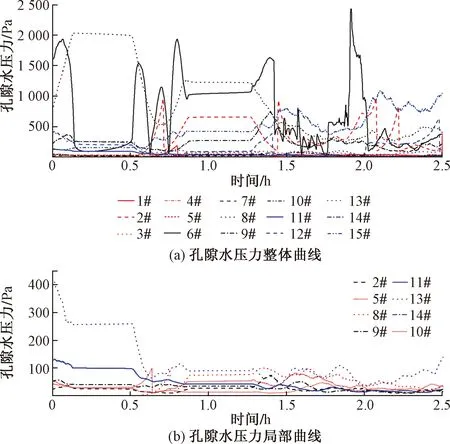
图11 孔隙水压力变化曲线Fig.11 Change curve of pore water pressure

从试验曲线分析来看，随着降雨时长的增加，所有斜坡含水率、孔隙水压力，土压力均不断增加，坡体稳定性降低。3组斜坡中，55°斜坡更易降雨入渗达到饱和，从而失稳下滑，而75°斜坡较陡降雨不易入渗，35°斜坡为自然斜坡，地表未受人为扰动，降雨也不易入渗。

2 滚石斜坡的失稳机理推导

通过野外调查和模型试验可知，滚石斜坡的失稳分为颗粒失稳滚动和局部滑动破坏，由于颗粒失稳滚动已经进行了相应的数值模拟和理论分析[5]，在此不再进行赘述。下面对滚石斜坡在降雨入渗条件下稳定性进行推导。

由于滚石边坡性质与土质边坡较为相似，岩土颗粒之间的咬合力和摩擦力均较大，将土体条分后，条块侧面的作用力不可忽略，在稳定性计算中利用简布法较为合理。从模型试验可知滑动面深度为入渗深度，但不超过土体与基岩的接触面，故计算的基本力学模型如图12所示。

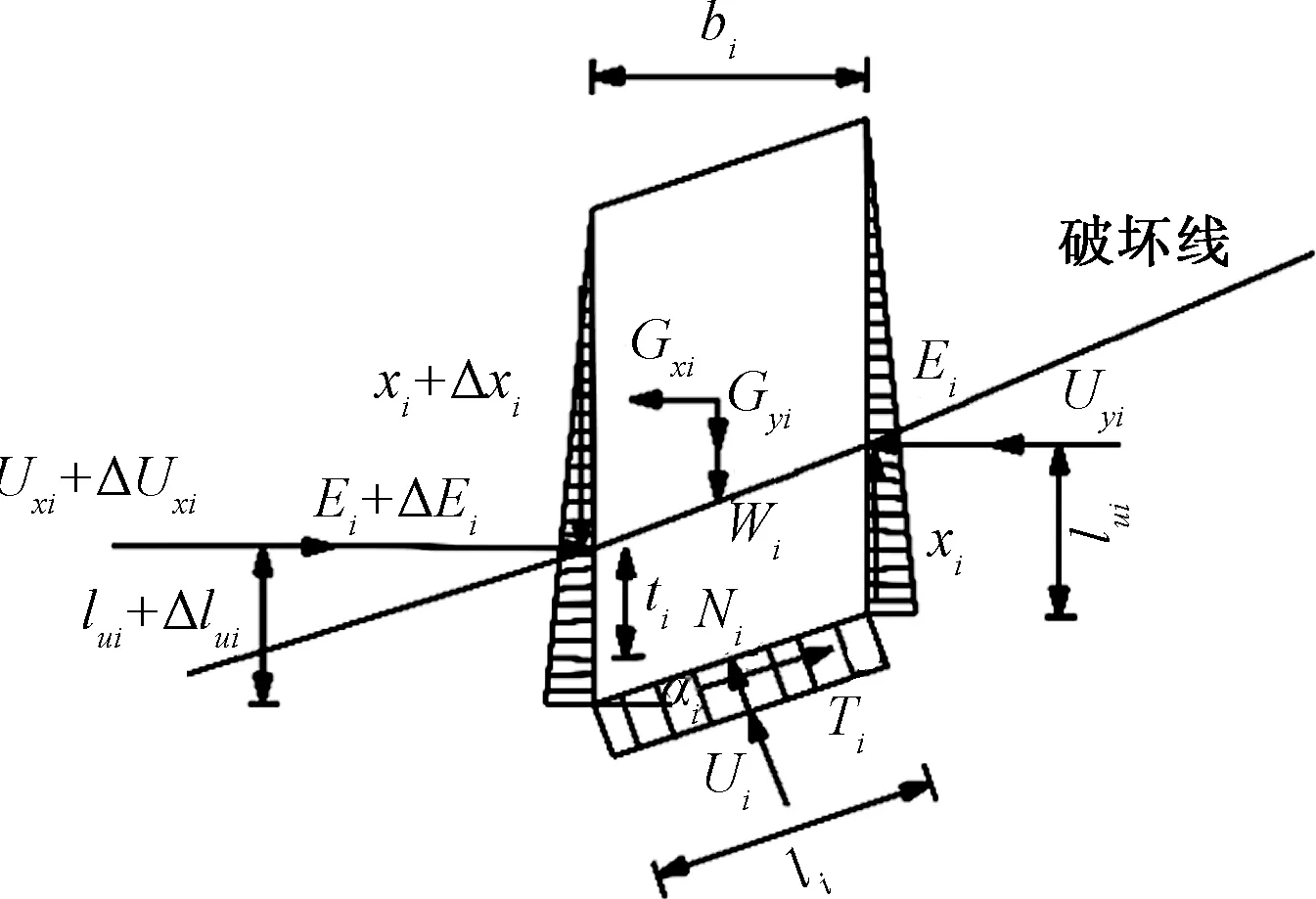
Ni为第i条块在滑面的法向力；Ti为第i条块在滑面的剪切力；li为第i条块滑面长度；Wi为第i条块的自重；xi为第i条块后侧侧向竖直力；xi+Δxi为第i条块前侧侧向竖直力；αi为第i条块滑面的倾角；Ui为第i条块的底部水压力；Ei为第i条块后侧侧向水平力；Ei+ΔEi为第i条块前侧侧向水平力；Uxi为第i条块后侧水压力；Uxi+ΔUxi为第i条块前侧水压力；bi为第i条块的宽度；Gyi为y方向的渗透力分量；Gxi为x方向的渗透力分量；lui为Uxi的作用点到条块底面的竖直距离；lui+Δlui为Uxi+ΔUxi的作用点到条块底面的竖直距离；ti为Ei+ΔEi作用点到条块底面中心的竖直距离

2.1 前提假定

(1)滑动面上切向力Ti等于滑动面上土所发挥的抗剪强度τfi，即

(1)

式(1)中：φi为第i条块滑面的摩擦角；ci为第i条块滑面的黏聚力；K为土坡稳定安全系数。

(2)给出土条两侧法向力E的作用点位置，为侧面下1/3处。条块的静水压力是由于降雨入渗的水产生的，忽略地表积水的厚度，静水压力的大小为γwh(γw为水的重度，h为降雨入渗深度)，两侧的静水压力的作用位置也为侧面下1/3处。

2.2 公式推导

根据土的竖向方向力学平衡∑Fy=0，有

Wi+(xi+Δxi)-xi-Nicosαi-Uicosαi-Tisinαi+Gyi+Pi=0

(2)

式(2)中：Pi为第i条块竖直向下的地震作用力。

式(2)经换算，可变为

(3)

根据土的水平方向力学平衡∑Fx=0，有

Ei-(Ei+ΔEi)+Nisinαi+Uisinαi-

Ticosαi+Uxi-(Uxi+ΔUxi)+Gxi+Pxi=0

(4)

式(4)中：Pxi为第i条块向坡前的地震作用力。

式(4)经换算，可变为

ΔEi=Nisinαi-Ticosαi+(Uisinαi-ΔUxi)+Gxi+Pxi

(5)

将式(3)代入式(5)，化简得

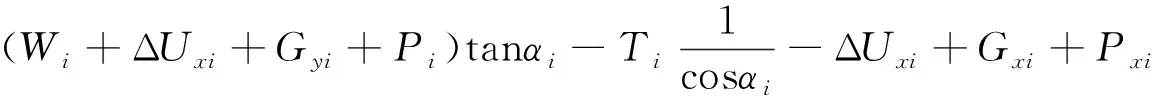
(6)

根据假设(1)，将式(3)和式(1)联立求解，化简可得

(7)

式(7)中：bi为第i条块的宽度。

为简化式(7)，令

(8)

将简化后的式(7)代入式(6)，得

(9)

式(9)中：

Bi=(Wi+Δxi+Gyi+Pi)tanαi

(10)

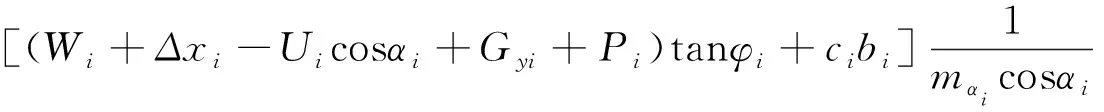
(11)

对于整个滚石斜坡而言，所有的ΔEi均为内力，若滑动土体上无水平外力作用时，则∑ΔEi=0，即

(12)

得滚石斜坡稳定安全系数K为

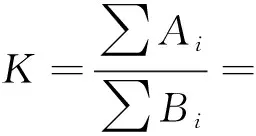
∑(Wi+Δxi+Gyi+Pi)tanαi

(13)

式(13)中:Δxi项仍然未知，需通过其他条件求解。根据假设(2)，土条上各作用力对滑动面中点取矩：

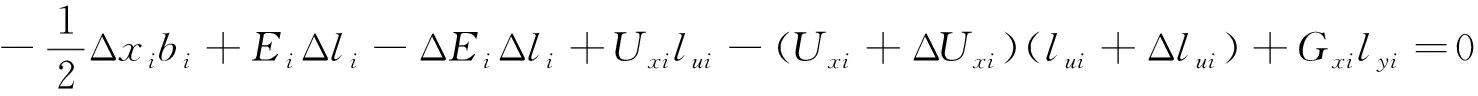
(14)

式(14)中：lyi为x方向的渗透力分量Gxi的作用点到条块底面的竖直距离。

如果土条宽度很小，则高阶项略去，并忽略水压力产生的弯矩，按力矩平衡可得

(15)

Ei是土条E1与各土条的ΔEi之和，则有

(16)

Δxi=xi+1-xi

(17)

式(13)等号右侧mαi包含了待求项K，是隐函数，需要采用迭代法计算求解。

3 结论

利用模型试验分析降雨和不同坡度条件下滚石斜坡的稳定性与含水率、孔隙水压力及土压力的映射关系，并结合试验推导了滚石斜坡稳定性的简布法，得出以下结论。

(1)随着降雨时长的增加，所有斜坡的含水率、孔隙水压力和土压力值均增加，其中55°斜坡含水率更易达到饱和值，验证了野外不稳定滚石坡集中在55°左右的主因。

(2)55°斜坡比75°和35°斜坡更利于降雨入渗，其含水率、土压力和孔隙水压力均为最大，从而更容易失稳滑动。分析其原因，75°斜坡较陡降雨不易入渗，35°斜坡为自然斜坡，地表未受人为扰动，降雨也不易入渗。

(3)降雨入渗条件下，滚石斜坡的失稳破坏首先是岩土颗粒滚落，然后是局部滑动破坏并不断扩大，与野外调查现象一致。

(4)结合模型试验，推导出滚石斜坡在降雨入渗条件下的简布法稳定性计算公式。

(5)从试验和理论推导进一步说明：降雨初期滚石斜坡表面岩土颗粒黏聚力和内摩擦角减小，岩土颗粒不断滚落；持续降雨使滚石斜坡整体含水率和孔隙水压力增加，最终导致斜坡失稳滑动。