推力矢量飞机鲁棒故障检测与辨识和指令滤波容错控制系统设计
李炳乾,钱 坤,严 浩,王发威
(空军工程大学 航空机务士官学校,河南 信阳 464000)
1 引言
随着航空武器装备的迅速发展以及作战任务的复杂变化,推力矢量技术[1–2]在现代空战中发挥着越来越重要的作用.推力矢量技术是指可以改变发动机推力方向的技术[3–4],可以确保飞机在大迎角、低空速情况下,完成超常规机动动作[5],通过绕速度矢量滚转,快速改变机头指向来迅速扭转敌我态势[6].我国在2018珠海航展上充分展示了推力矢量技术的优越性.但是推 力矢量飞机(thrust-vectoring aircraft,TVA)在超机动过程中,容易受到强非线性和强耦合的气动力[7],必然存在参数摄动和外界干扰的问题,同时强烈的气流会增大舵面和执行器的故障率,不仅影响作战任务的完成,甚至会造成机毁人亡的严重后果.因此,针 对TVA进行故障检测和 容错控 制方法 的研究,具有重要的意义.
当舵面和执行器发生故障时,舵面偏转的角度和速度会发生变化,舵面所提供的气动力和气动力矩也会发生相应变化,最终导致TVA的飞行姿态也随之变化[8].TVA安装有可以实时测量舵面偏转角度和速度的传感器,当舵面发生异常偏转时,传感器可以捕捉到这一变化,检测并诊断故障.另外一方面,TVA安装有姿态角和角速度传感器,当传感器检测姿态和角速度是否发生异常变化,就可以诊断是否发生故障了.当TVA推力矢量上下偏转时,可以补偿俯仰力矩;当TVA推力矢量左右偏转时,可以补偿偏航力矩;而当TVA推力矢量同时上下、左右偏转,可以补偿滚转力矩.因此,TVA飞行系统对于舵面故障和执行器故障具有可诊断性与可重构性[9].
故障检测与辨识是容错控制的重要组成部分,近年来针对容错检测与辨识的研究取得了一定的进展.文献 [10]提出了一种基于模型的故障检测与辨识方法,通过提取故障信息,并根据故障信息与自适应观测器之间的残差来检测和辨识故障.仿真结果验证了该方法的有效性,但是此方法忽略了参数和外界干扰等不确定性对检测结果的影响.文献 [11]针对一类连续分段仿射系统,提出了一种在线故障检测与辨识方法,通过设计自适应律来补偿参数不确定性,可以快速、准确检测故障,但是没有考虑外界干扰的影响.文献 [12]针对导航系统,提出了一种基于信任规则的故障检测模型,利用系统测量的残差和变化率作为信任规则的输入,并引入了参数递归估计算法.由于该方法忽略了扰动和不确定性的影响,可能会出现虚警.文献 [13]针对带有参数和外界干扰等不确定性的卫星姿态系统,提出了一种执行器故障检测和容错控制方法,但是此方法不能够准确辨识和估计执行器的故障类型和故障参数.文献 [14]提出了一种多操纵面执行器卡死故障的检测算法,通过偏差估计算法来估计执行器卡死的位置,并利用自适应观测器来检测故障.该方法考虑的故障类型比较单一,并且没有考虑外界干扰等不确定性的影响,不符合工程实际要求.通过以上分析可以看出,在故障检测方法的设计过程中,大部分文献没有考虑到TVA超机动飞行所带来的外界干扰和参数摄动问题,这可能会导致较高的虚警率.并且,大多数文献不能够准确辨识类型,估计故障参数.因此,本文提出一种新颖的鲁棒故障检测与辨识(robust fault detection and identification,RFDI) 机制,能够保持对外界干扰和参数摄动的鲁棒性,以及对舵面故障和执行器故障的敏感性.
舵面故障和执行器故障会严重威胁TVA的飞行安全,因此需要在故障检测与辨识的基础上设计容错控制方 法.文献 [15]针对带 有冗余执行器的飞行系统,提出了一种基于积分滑模技术的控制分配方法,能够实现包容执行器故障的容错控制.文献 [16]针对带有冗余机构和垂直尾翼损伤的飞行系统,通过线性二次调节器和模型参考自适应方法来重新进行控制分配,实现针对方向舵损伤的容错控制.文 [17]通过矩阵变换将非线性系统的执行器故障及传感器故障结合,针对故障及干扰设计鲁棒滑模观测器,实现对执行器和传感器故障及干扰的容错控制.但是矩阵变换及滑模观测器需满足较为严格的条件.文献 [18]首先通过坐标变换将系统状态分为是否包含执行器故障两部分,然后在滑模观测器中引入H∞鲁棒控制补偿不确定性,实现对执行器故障的估计.同时对系统传感器故障采用相同的方法估计,二者并列进行.此方法故障估计效果较好,但是计算较为复杂且限制条件较为严格.文献 [19]将故障及干扰作为滑模观测器的输入,其输出又作为下一个观测器的输入,此过程不断重复直至满足故障和干扰同时解耦的条件,取得了较好的控制效果.但是此方法对故障输入矩阵和输出矩阵作了严格要求,不具有一般性.上述分析表明,大多数文献并没有同时考虑到舵面故障、执行器故障、参数摄动和外界干扰对TVA超机动飞行的影响,因此本文在RFDI的基础 上,提出了一种指令滤波容错控制(command fltering fault-tolerant control,CFFTC)控制律.
本文针对TVA在超机动飞行中的舵面故障、执行器故障、参数摄动和外界干扰等问题,提出了一种新颖的鲁棒故障检测与辨识和指令滤波容错控制(robust fault detection and identifcation and command fltering fault-tolerant control,RFDI–CFFTC) 系统设 计方法,创新点主要有:1) 能够保持对超机动飞行中参数摄动和外界干扰的鲁棒性,对舵面故障和执行器故障的敏感性,能够有效降低虚警律,提高故障检测的准确性;2) 能够在参数摄动和外界干扰的影响下,快速、准确检测并辨识舵面故障、执行器卡死故障和执行器损伤故障,同时准确估计故障参数的大小;3) 能够克服传统反步法中的“微分爆炸”问题,实现包容舵面故障、执行器故障、参数摄动和外界干扰的TVA容错控制.
2 模型描述
本节对包含舵面故障、执行器故 障、参数摄动和外界干扰的TVA故障模型进行描述.
2.1 TVA模型
根据奇异摄动理论,TVA运动模型可以分为姿态角回路和角速度回路[1],表达式如下:
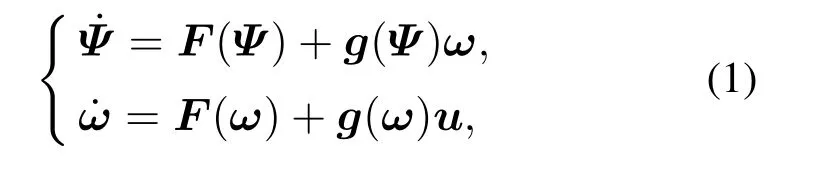
式中:Ψ=[α β µ]T表示姿态角回路,分别为TVA的迎角、侧滑角和滚转角;ω=[p q r]T表示角速度回路,分别为TVA的滚转、俯仰和偏航角速度;F(Ψ)和F(ω)分别为姿态角回路和角速度回路的非线性部分;g(Ψ)和g(ω)分别为系数矩阵;u=[δaδeδrδyδz]T分别为副翼、升降舵、方向舵、侧向推力矢量和纵向推力矢量偏转角度.
TVA在超机动飞行过程中,强非线性和强耦合的不稳定气流会引起气动参数摄动,并且引入未知的外界干扰d,则TVA模型可以进一步描述为

式中:f(Ψ)和f(ω)分别为姿态角回路和角速度回路的非线性部分;ηΨ∈R3和ηω∈R12分别表示TVA的气动力参数和气动力矩参数;A(Ψ)和B(ω)分别为气动力参数和气动力矩参数的系数矩阵.
2.2 舵面故障模型
当TVA在超机动飞行时,不稳定气流会增加舵面发生故障的概率.当舵面发生故障时,主要表现为舵面的气动作用发生改变[20],则舵面故障可以描述为

式中:i=a,e,r,y,z;表示第i个舵面发生故障时,产生实际气动作用的等效舵面偏角;δi为第i个执行器向舵面输入的偏转指令;ri∈(0,1]表示第i个舵面的故障参数,其中ri=1表示舵面无故障,ri∈(0,1)表示舵面发生一定程度的故障.则TVA的舵面故障模型可以表示为

式中R=diag{ra,re,rr,ry,rz}.
2.3 执行器故障模型
TVA在超机动飞行过程中,典型的执行器故障主要有损伤故障和卡死故障两种[21],可以表示为
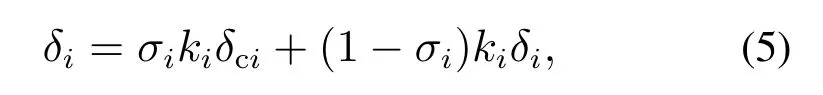
式中:δci表示执行器的输入指令;σi∈ {0,1}表示执行器卡死时的故障系数,σi=0表示发生卡死故障,σi=1表示没有发生卡死故障;ki∈(0,1]表示执行器损伤时的故障系数,ki=1表示未发生损伤故障,ki∈(0,1)表示发生一定程度的损伤故障.则包含舵面故障、执行器故障、参数摄动和外界干扰的TVA故障模型可以描述为

式中:
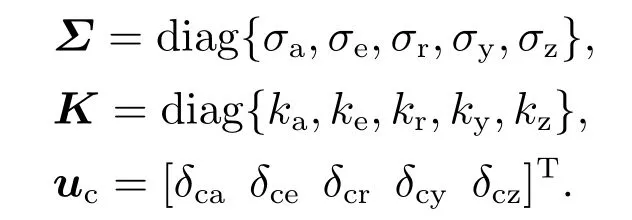
3 RFDI机制设计
传统的故障检测方法,容易受到参数摄动及气流扰动和模型误差等不确定性的影响,而出现较高的虚警率.为了准确检测和辨识TVA故障,本节提出了一种具有鲁棒性的故障检测与辨识(RFDI)机制,主要包括3个部分:一是故障检测部分,实现在参数摄动和外界干扰的影响下,对TVA是否发生故障进行检测;二是故障辨识部分,实现对舵面故障和执行器故障的辨识;三是执行器故障类型辨识部分,实现对卡死故障和损伤故障的辨识.
3.1 故障检测
针对TVA模型(2),设计如下自适应观测器:



3.2 故障辨识
针对TVA模型(4),设计如下自适应观测器:

由定理2可以得到,舵面故障和执行器故障的辨识方法如下:

式中T2是故障辨识阈值.
3.3 执行器故障类型辨识
本小节针对每个执行器,分别设计卡死故障自适应观测器和损伤故障 自适应 观测器来辨识执行器故障类型.
设计卡死故障自适应观测器如下:


3.4 RFDI流程图
总结整理可以得到RFDI的流程图如图1所示.

图1 RFDI流程图Fig.1 Flow diagram of the RFDI
4 CFFTC控制律设计
本节提出了一种指令滤波容错控制律(CFFTC)设计方法,将姿态角回路输出的虚拟控制指令经滤波器滤波后,输出到角速度回路中,来避免传统反步法中的“微分爆炸”问题;同时引入自适应律来补偿TVA的舵面故障、执行器 卡死故障、执行器损伤故障、外界干扰和参数摄动,实现TVA容错控制.
4.1 姿态角回路控制律设计

4.2 角速度回路控制律设计


4.3 CFFTC控制律设计
本小节设计滤波器来对式(40)的虚拟指令进行滤波,避免“微分爆炸”问题,滤波器的结构图如图2所示.
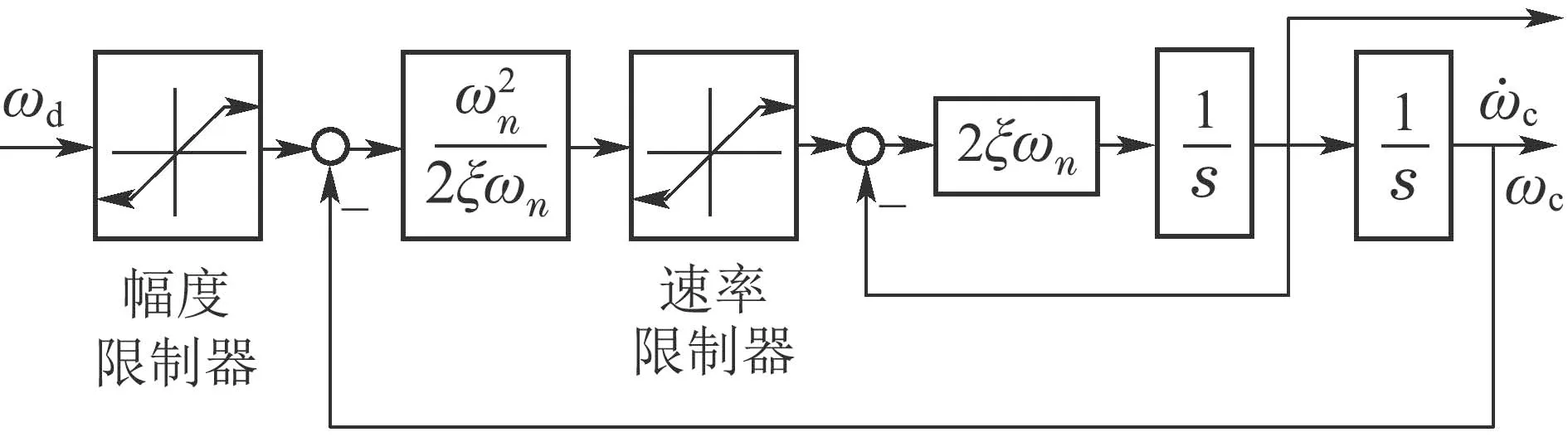
图2 滤波器结构图Fig.2 Structure of the filter
滤波器的状态空间方程为
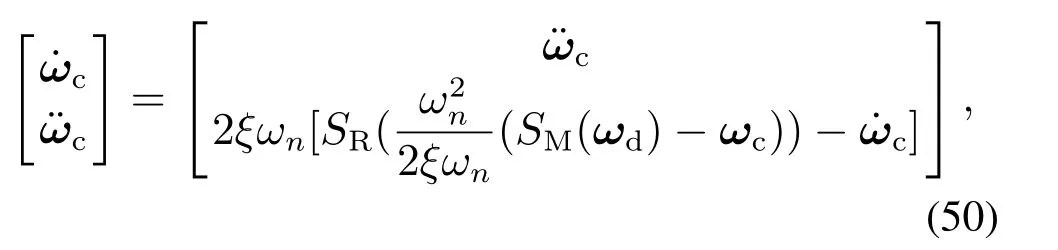
式中:ξ和ωn分别为滤波器的阻尼和带宽;ωc是虚拟指令ωd经滤波器滤波后的值;SR(·),SM(·)分别表示速率和幅值饱和函数.则滤波器的误差Ω为
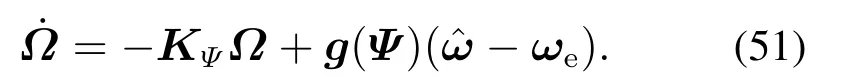
则TVA的姿态角误差可以重新定义为
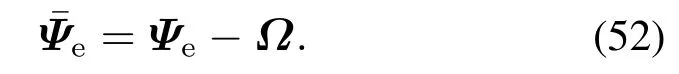
TVA的角速度误差可以重新定义为

则CFFTC控制律设计为
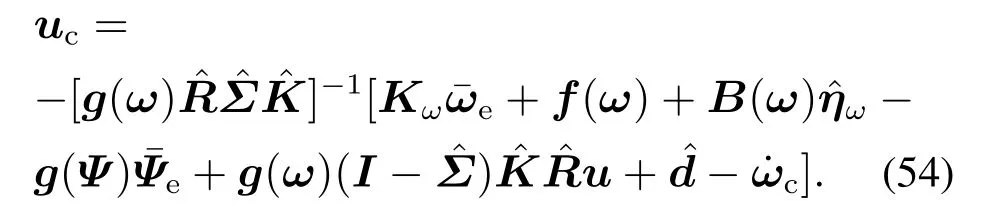
定理7针对TVA的角速度回路,设计CFFTC控制律(54),则角速度回路渐进稳定,即
证 构建如下Lyapunov函数:
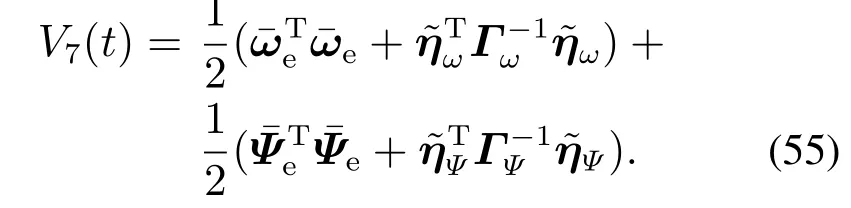
对上式求导,并将式(47)(49)–(51)(54)–(55)和 式(58)代入可得

由Lyapunov稳定性定理可以得到,所设计的CFFTC控制系统稳定,即证毕.
5 RFDI–CFFTC系统稳定性分析
定理8针对包含舵面故障、执行器故障、参数摄动和外界干扰的 TVA 故障模型 (6),本文所设计的RFDI–CFFTC系统渐 进稳定,主要包 括CFFTC控 制律(54)、舵面故障自适应律(21)、执行器卡死故障自适应律(26)、执行器损伤故障自适应律(30)、外界干扰观测器(10)、参数自适应律(41)和(45).
证构建如下Lyapunov函数:

对上式求导,并将式(10)(21)(26)(30)(41)(45)和式(54)代入化简可得
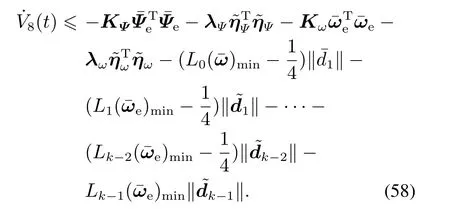
所设计的RFDI–CFFTC系统结构图如图3所示.
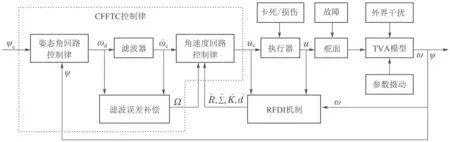
图3 RFDI–CFFTC系统结构图Fig.3 The block diagram of the RFDI-CFFTC system
6 仿真验证
本节针 对X–31验证机进行MATLAB/Simulink仿真,来验证本文所设计的RFDI–CFFTC系统的有效性.
6.1 控制律参数
经过不断调试,设置指令滤波器参数为ξ=0.8,ωn=12 rad/s,速率约束为±25(◦)/s;幅值约束为±40◦;设置RFDI–CFFTC控制律参数如表1所示.
6.2 故障设置
设置仿真时长为10 s,仿真步长为0.001 s.设定参数摄动为
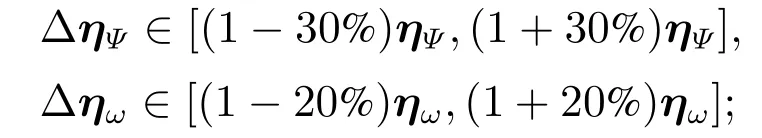
外界干扰为

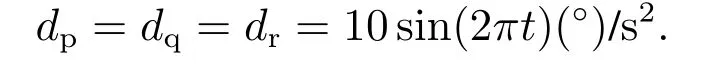
故障设置如表2所示.

表1 RFDI–CFFTC控制律参数Table 1 Parameters of RFDI–CFFTC control law
6.3 仿真结果与分析
6.3.1RFDI仿真结果
选取阈值T1和T2为0.1,分别针对情景1、情景2和情景3进行RFDI仿真.
情景1为了验证自适应观测器(7)对参数摄动和外界干扰的鲁棒性,在情景1条件下,分别对自适应观测器(7)和不包括自适应律(8)、观测器(10)的一般观测器进行仿真,一般观测器的误差记为.
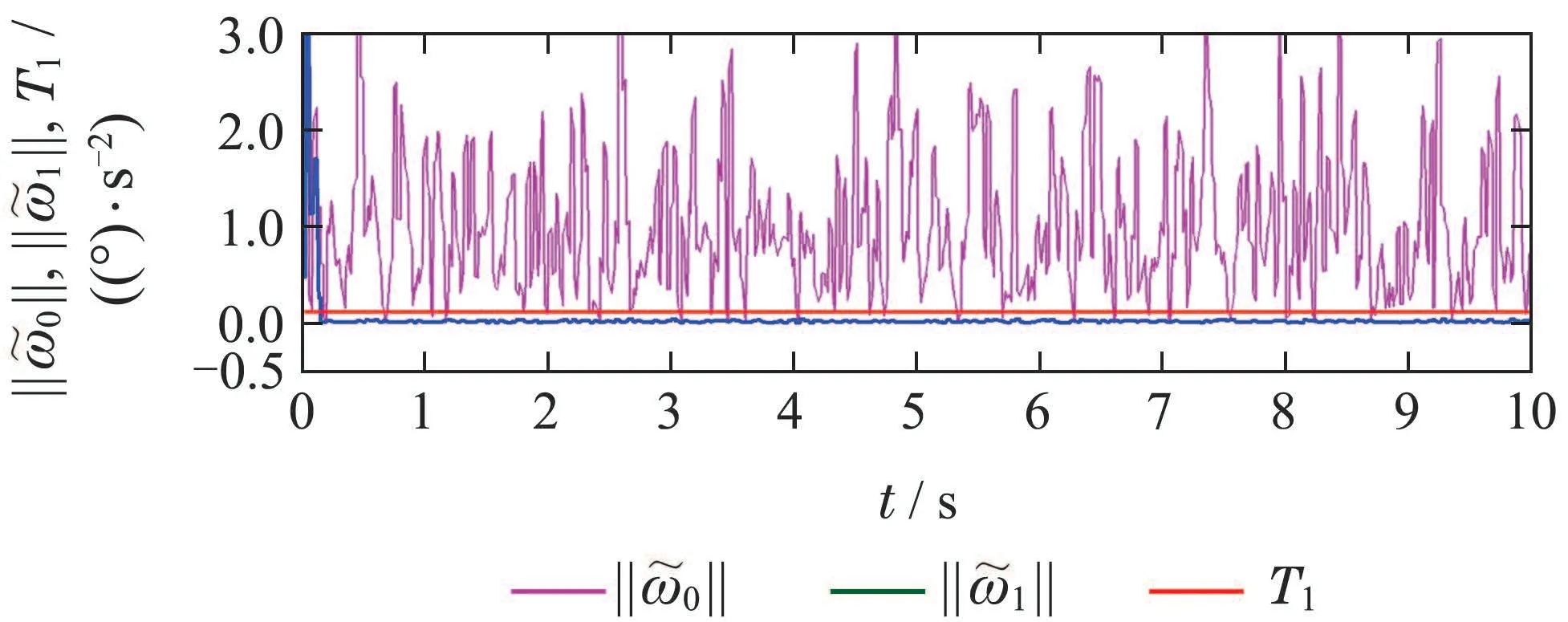
图4 情景1的故障检测结果Fig.4 Fault detection result of Condition 1
情景2故障检测与辨识的仿真结果如图5所示,可以看出:在仿真开始后迅速收敛至阈值T1以下,而在t=3 s,5 s,7 s时,越过阈值T1;‖˜ω2‖则在仿真开始后迅速收敛至阈值T2以下直至仿真结束.通过对比可以判断出,t=3 s,5 s,7 s时,TVA有舵面故障发生.

图5 情景2的故障检测与辨识结果Fig.5 Fault detection and identification result of Condition 2
故障参数估计结果如图6所示,可以看出:t=3 s时,副翼舵面发生80%的故障;t=5 s时,升降舵舵面发生70%的故障;t=7 s时,方向舵舵面发生60%的故障.仿真结果与故障设置相同,验证了本文所设计的RFDI对舵面故障检测与辨识的有效性.
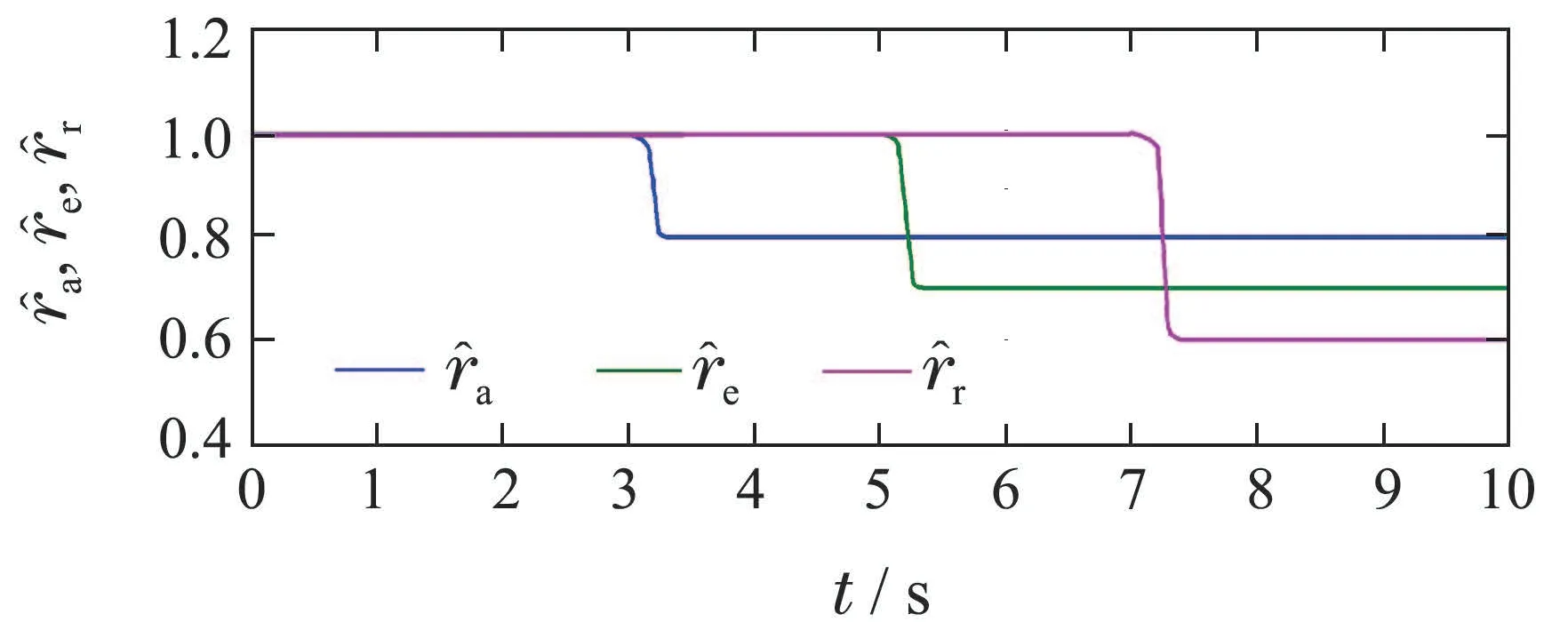
图6 情景2的故障参数估计结果Fig.6 Fault parameter estimation results of Condition 2
情景3故障检测与辨识的仿真结果如图7所示,可以看出:在仿真开始后迅速收敛至阈值T1以下,而在t=3 s,4 s,5 s,6 s,7 s时,越过阈值T1;在仿真开始后迅速收敛至阈值T2以下,而在t=3 s,4 s,5 s,6 s,7 s 时,越过阈值T2.通过对比可以判断出,t=4 s时,TVA有舵面故障发生;t=3 s,5 s,6 s,7 s 时,TVA有执行器故障发生.

图7 情景3的故障检测与辨识结果Fig.7 Fault detection and identification result of Condition 3
故障参数估计结果如图8所示,可以看出:t=3 s时,升降舵执行器发生70%的损伤故障;t=4 s时,副翼舵面发生70%的故障;t=5 s时,方向舵执行器发生60%的损伤故障;t=6 s时,升降舵执行器发生卡死故障;t=7 s时,方向舵执行器发生卡死故障.仿真结果与故障设置相同,验证了本文所设计的RFDI对舵面故障和执行器故障检测与辨识的有效性.

图8 情景3的故障参数估计结果Fig.8 Fault parameter estimation results of Condition 3
综合以上分析,可以验证本文所设计的RFDI机制,对参数摄动和外界干扰具有鲁棒性,而对舵面故障和执行器故障具有敏感性,能够快速、准确检测并且辨识出故障类型,估计出故障参数的大小.
6.3.2 RFDI–CFFTC仿真结果
为了验证本文所设计的RFDI–FTC系统对舵面故障、执行器故障、参数摄动和外界干扰的容错性能,分别对FTC控制律(47)、CFFTC控制律(54)以及不包含舵面故障 自适应律(21)、执行器卡死故障 自适应律(26)、执行器损伤故障自适应律(30)、参数自适应律(41)和(45) 和外界干扰观测器(10)的一般控制律进行对比仿真.TVA中δa,δe,δr,δy和δz的最大偏转角度分别为±15◦,±15◦,±15◦,±20◦和±20◦.仿真结果如图9–11所示.
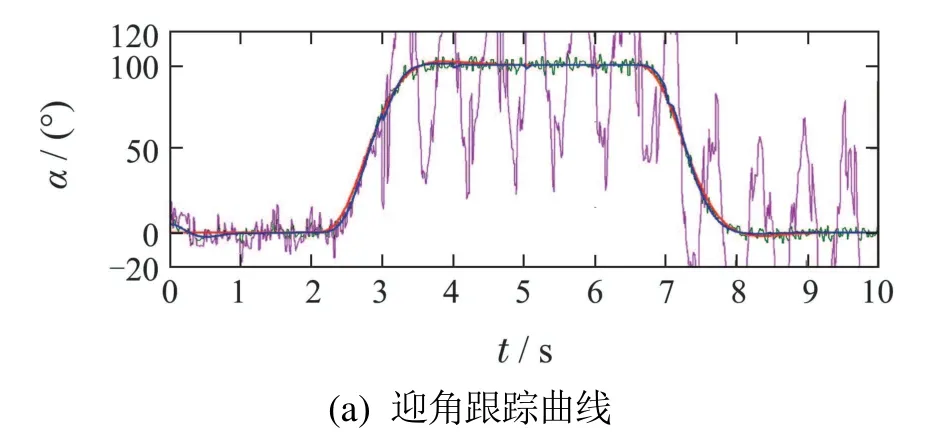

图9 姿态角回路跟踪曲线Fig.9 The trace signal of the attitude-angle-loop
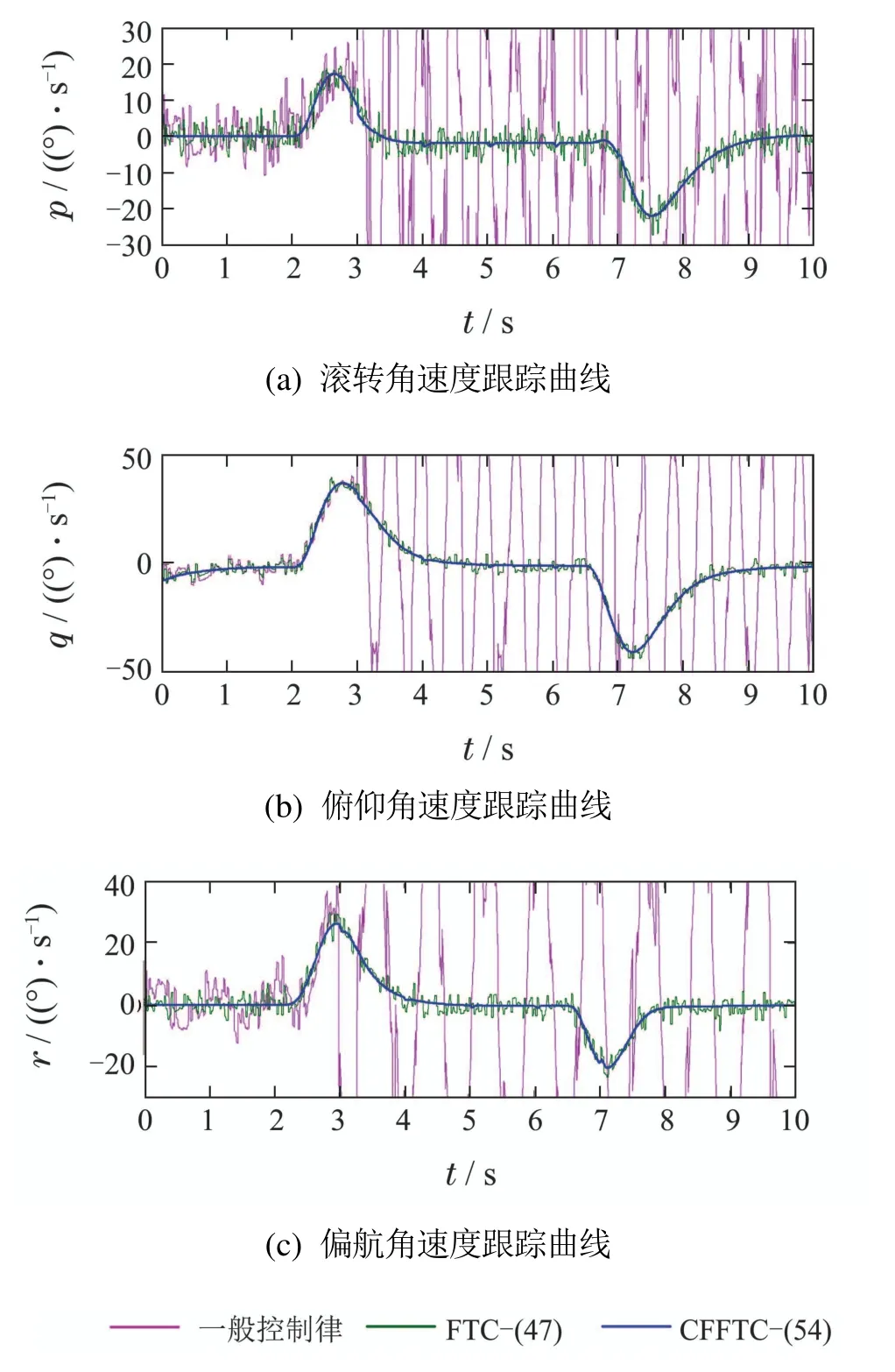
图10 角速度回路跟踪曲线Fig.10 The trace signal of the angle-velocity-loop
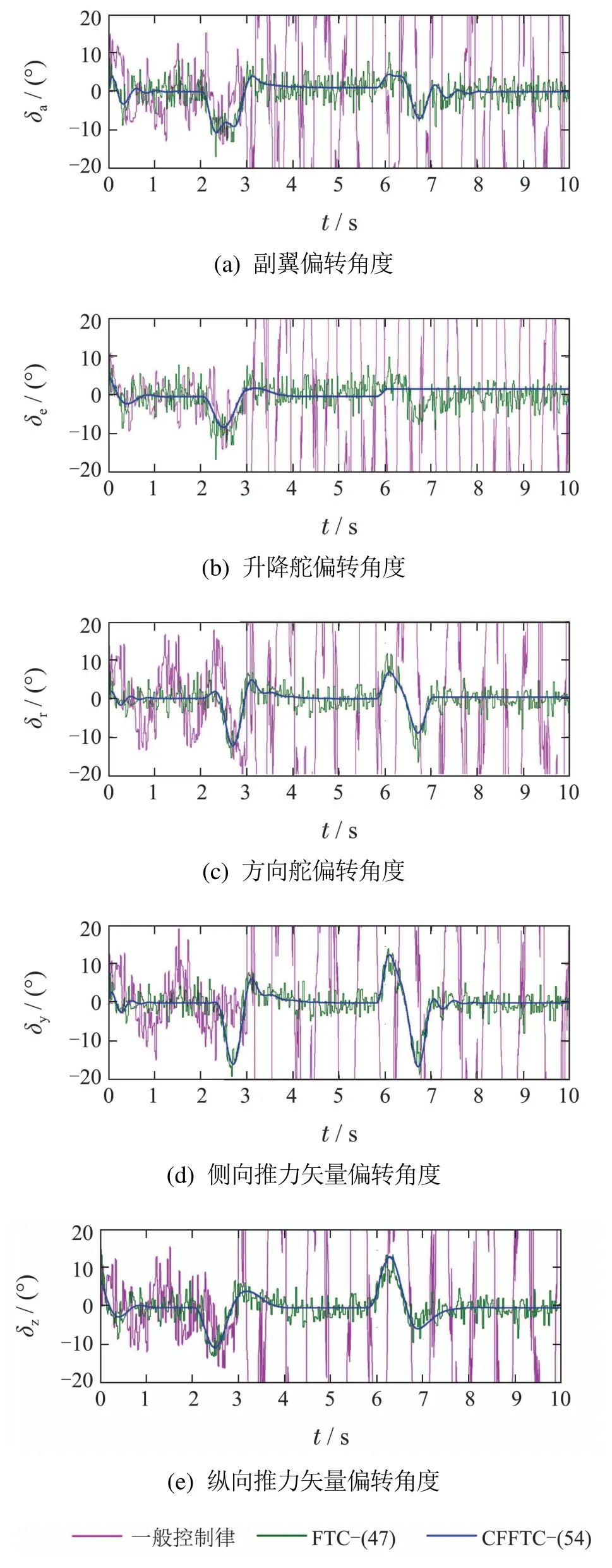
图11 舵面偏转角度Fig.11 The deflection angle of the control surface
图9为TVA姿态角回路的跟踪曲线,可以看出:在一般控制律作用下,0~3 s时,姿态角的误差较大,不能实现包容参数摄动和外界干扰的鲁棒控制;而在t=3 s之后,姿态角剧烈振荡,振荡幅度和频率都比较大,不能实现包容舵面故障和执行器故障的容错控制.FTC–(47)可以大致跟踪指令信号,但是会有不规则的波动,而CFFTC–(54)则可以稳定、快速、准确跟踪姿态角指令信号.通过对比可以看出,本文所设计的CFFTC–(54)能够实现对参数摄动和外界干扰的鲁棒控制,对舵面故障和执行器故障的容错控制,同时能够包容传统反步法中“微分爆炸”的影响,控制效果较好.
图10为TVA角速度回路的跟踪曲线,与图9的分析过程类似.
图11是舵面偏转角度仿真曲线,可以看出:在一般控制律作用下,TVA的舵面偏转角度发生大幅度的剧烈振荡,并在t=3 s后,完全发散;在FTC–(47)的作用下,舵面偏转角度发生不规则振荡,不能满足TVA的实际飞行要求;而在FTC–(54)的作用下,舵面偏转角度稳定变化,同时能够限制在±15◦,±15◦,±15◦,±20◦和±20◦内,满 足TVA的实际飞行要 求.另外一方 面,舵面偏 转角度 在t=3 s,5 s,6 s和 7 s时的变化,验证了TVA的推力矢量能够在一定程度上补偿气动舵面的作用.
整个仿真过程验证了本文所设计的RFDI–CFFTC系统,能够快速、准确检测、辨识故障类型,估计故障参数,同时能够实现包容舵面故障、执行器故障、参数摄动和外界干扰的TVA容错控制.
7 结论
本文提 出了一 种新颖 的推力 矢量飞 机 RFDI–CFFTC系统设 计方法,通 过MATLAB/Simulink仿 真验证,可以得到以下结论:
1) 本文所设计的RFDI–CFFTC系统能够保持对参数摄动和外界干扰的鲁棒性,对舵面故障和执行器故障的敏感性,能够有效降低虚警律,提高故障检测的准确性.
2) 本文所设计的RFDI–CFFTC系统能够在参数摄动和外界干扰的情况下,快速、准确检测并辨识舵面故障、执行器卡死故障和执行器损伤故障,同时准确估计故障参数的大小.
3) 本文所设计的RFDI–CFFTC系统能够克服传统反步法中的“微分爆炸”问题,实现包容舵面故障、执行器故障、参数摄动和外界干扰的TVA容错控制.

