带有干扰观测器的线控转向系统复合自适应神经网络控制

王云龙 ,王泽政 ,王永富 ,赵 晶

(1.东北大学 机械工程与自动化学院,辽宁 沈阳 110819;2.北京航空航天大学 自动化科学与电气工程学院,北京 100083)

1 引言

随着汽车电子技术的不断发展,汽车已经由传统机械为基础的硬件主导演进为以电控技术为基础的软件主导.作为目前汽车线控技术的一种,线控转向(steer-by-wire,SbW)系统取消了方向盘与转向执行器之间的机械连接,通过电信号传输控制命令实现车辆转向,极大地改善了汽车的操纵稳定性、乘坐舒适性与安全性[1–2].

众多学者已 对SbW转向系统 控制问题进行了研究.文 献 [3–5]通过比 例微分 (proportional-derivative,PD) 控制实现了前轮转角跟随驾驶员的转向意图.但由于汽车在转向的过程中受到摩擦力矩、轮胎回正力矩与路况变化等因素影响,具有固定增益的PD控制器很难满足车辆在复杂工况下的转向性能.文献 [6]将线性二次型控制应 用在SbW系 统中,并与传统PD控制进行了比较,结果表明该控制器改善了车辆的跟踪性能.文 献 [7]基 于车辆模型设计 了跟踪控制 器.然 而,考虑到系统中存在不确定动态,SbW转向系统难以获取精确的动力学模型,因此基于模型控制器也不易获得理想的控制效果.

为了解决SbW系统中存在的不确定动态和外界干扰,保证前轮转角高精度的跟踪性能,自适应控制、滑模控制和神经网络等智能控制方法已得到研究人员的广泛关注.文献 [8]通过估计前轮胎的侧偏刚度,提出了一种自适应控制方 法实现车辆的转向特性.文献 [9]通过在线估计车辆的未知参数,并将自适应极点配置与PD控制结合保证了车辆的定向控制.然而,上述文献并未对其进行严格的稳定 性理论分析.基 于Lyapunov稳定性理论,滑模控 制广泛 应用于SbW系统,并实现转角的跟踪控制[10–12].但该类控制器的设计需要已知参数不确定及干扰的界.神经网络与模糊逻辑系统具有一致逼近和自适应能力,能够起到非线性在线逼近与补偿等作用[13–15].文献 [16]使用神经网络在线逼近参数不确定的界,并结合非奇异终端滑模控制方法保证车辆在不同工况下的转向性能.然而,上述神经网络自适应学习率仅由系统的跟踪误差进行调节,而没有考虑系统建模误差的影响.在SbW系统存在建模不确定性的情况下,关于如何有效利用建模误差构造神经网络自适应率实现车辆前轮转角快速跟随还需要进一步深入研究.基于以上分析,本文针对SbW系统提出了一种利用建模误差向量和跟踪误差向量共同调节神经网络自适应学习率的方法,提高了系统跟踪误差的收敛速度,并设计了一种新的二阶低通滤波辨识模型降低了测量噪声对系统的影响.

另外,由于未知外界干扰等各种不确定性因素广泛存在于实际工程系统中,所以在一定程度上影响了控制系统的稳定性[17].干扰观测器技术因其具有明确的物理意义,在工程实现上相对简单,常用于估计不确定系统中的干扰,所以得到了学术界与工程领域的广泛关注[18–20].考虑到SbW系统受到的摩擦力矩、回正力矩和神经网络逼近误差等复合干扰的影响,本文利用干扰观测器技术对复合干扰进行估计,将估计值反馈给控制器进行实时补偿,提高了系统抗干扰 能力[21–22].与目前已应用在SbW系统技术相比,本文所提出的控制方法不再需要系统不确定动态与外界干扰的先验知识,而是通过神经网络在线逼近系统不确定动态以及使用干扰观测器对复合干扰进行估计与补偿.最后,基于Lyapunov理论证明了闭环系统的跟踪误差信号一致最终有界,不同工况下的仿真和实验对比验证了所提出控制器的有效性和优越性.

2 SbW系统模型与问题描述

与传统的转向系统不同,SbW系统取消了从转向柱到转向器之间的机械连接,而是由转向电机总成、路感电机、转向器和传感器等部件组成.通过接收前轮转角信号,对转向电机发送转矩命令控制前轮转角,保证前轮转角快速跟随参考角度,实现驾驶员的转向意图,其系统结构如图1所示.

图1 SbW系统结构示意图Fig.1 The structure schematic of SbW system

SbW系统动力学方程可表示为[23]

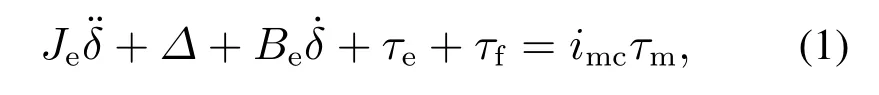
式中:

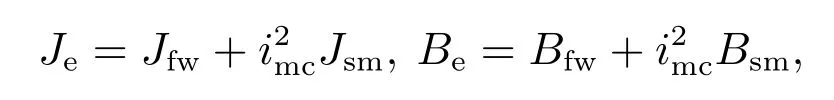
Je,Jfw,Jsm分别为系统等效转动惯量、前轮转动惯量和转向电机总成转动惯量;Be,Bfw,Bsm分别为系统等效阻尼系数、前轮阻尼系数和转向电机总成阻尼系数;∆为系统的建模不确定性,δ为前轮转角,imc为转向电机总成与转向前轮之间的传动比,τm为转向电机总成输出转矩,τe为前轮回正力矩,τf为前轮摩擦力矩.摩擦力矩可表示为如下模型[24]:

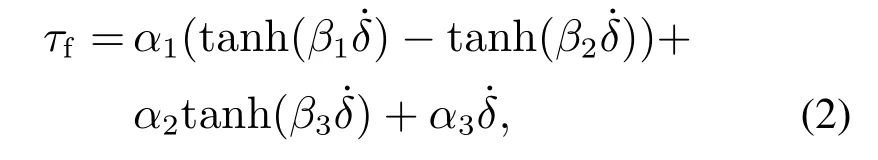
式中αi,βi(i=1,2,3)是与实际对象有关的正常数.

回正力矩τe可表示为[23]

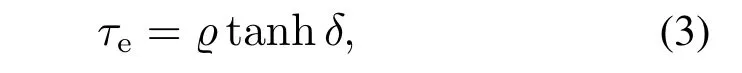
式中ϱ为与地面路况有关的正常数.

选 取车辆前轮转角δ为系统输出,根据式(1)可得SbW系统状态空间方程为

由于实际中很难获得系统不确定动态α(xxx)和外界干扰d的先验知识,因此控制器(5)的设计难以实现,故采用神经网络逼近不确定动态α(x),同时设计干扰观测器对外界干扰和神经网络逼近误差组成的复合干扰进行估计,保证前轮转角的跟踪控制.为了便于控制器的设计与分析,本文给出以下相关假设与引理:

假设1[20]系统外界干扰d及其导数有界,且存在未知常数,dmax使得成立.

对于SbW系统来说,本文所阐述的外界干扰d包括车辆前轮的回正力矩τe与摩擦力矩τf.在一定车速下,回正力矩τe为前轮转角δ的双曲正切函数,考虑到双曲正切函数及其导数为有界函数,故回正力矩τe是有界的.同时实际SbW系统中前轮转角角速度信号与角加速度信号大小是有限的,故回正力矩的导数也是一个有界函数.另外,由文献 [25]可知,摩擦力矩τf及其导数有界.综上所述,SbW系统受到的外界干扰满足假设1.

引理1[14]作为一种线性参数化神经网络,径向基函数神经网络(radial basis function neural network,RBFNN)能以任意精度逼近紧致集上的任意连续实函数Fnn(x):Rm→R,具体表示为

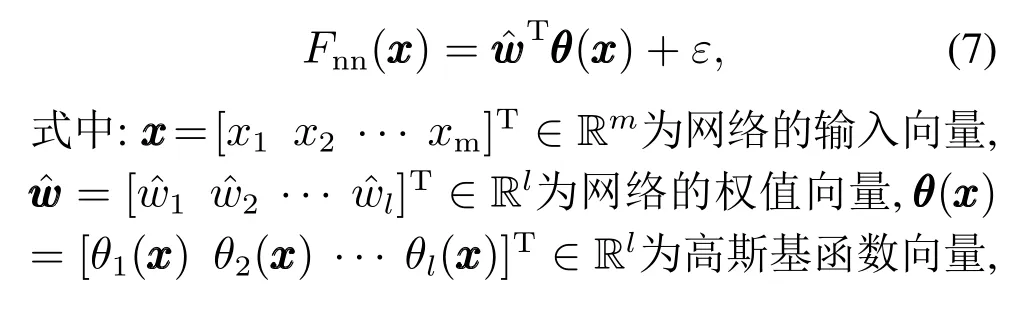
3 含干扰观测器的复合自适应神经网络控制器设计

3.1 复合自适应神经网络学习率设计

与仅由跟踪误差调节的神经网络自适应学习率不同,文献 [27]首先引入系统辨识模型,并通过构造建模误差和跟踪误差共同调节神经网络自适应学习率,加速了系统跟踪误差的收敛.但该辨识模型中的高阶信号是通过差分法获得,会受到传感器测量噪声的影响.文献 [28–29]提出了一阶低通滤波的辨识模型,它克服了文献 [27]中辨识模型需要已知高阶信号的缺点.针对SbW系统,该一阶低通滤波的辨识模型设计如下:

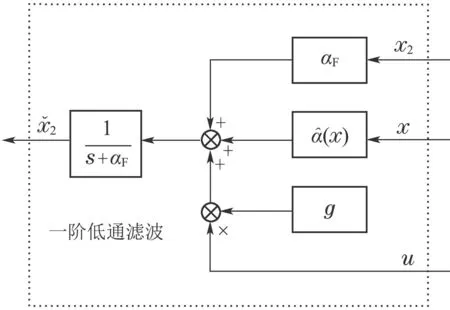
图2 一阶低通滤波辨识模型Fig.2 Identification model with first-order low-pass filter

为了更进一步改善系统跟踪误差收敛速度并同时提高系统的抗噪能力,受文献 [28]的启发,本文结合干扰观测器,提出二阶低通滤波的辨识模型:

选择参数kF1和kF2能够使二阶低通滤波的辨识模型更进一步衰减测量噪声[30],辨识模型结构如图3所示.

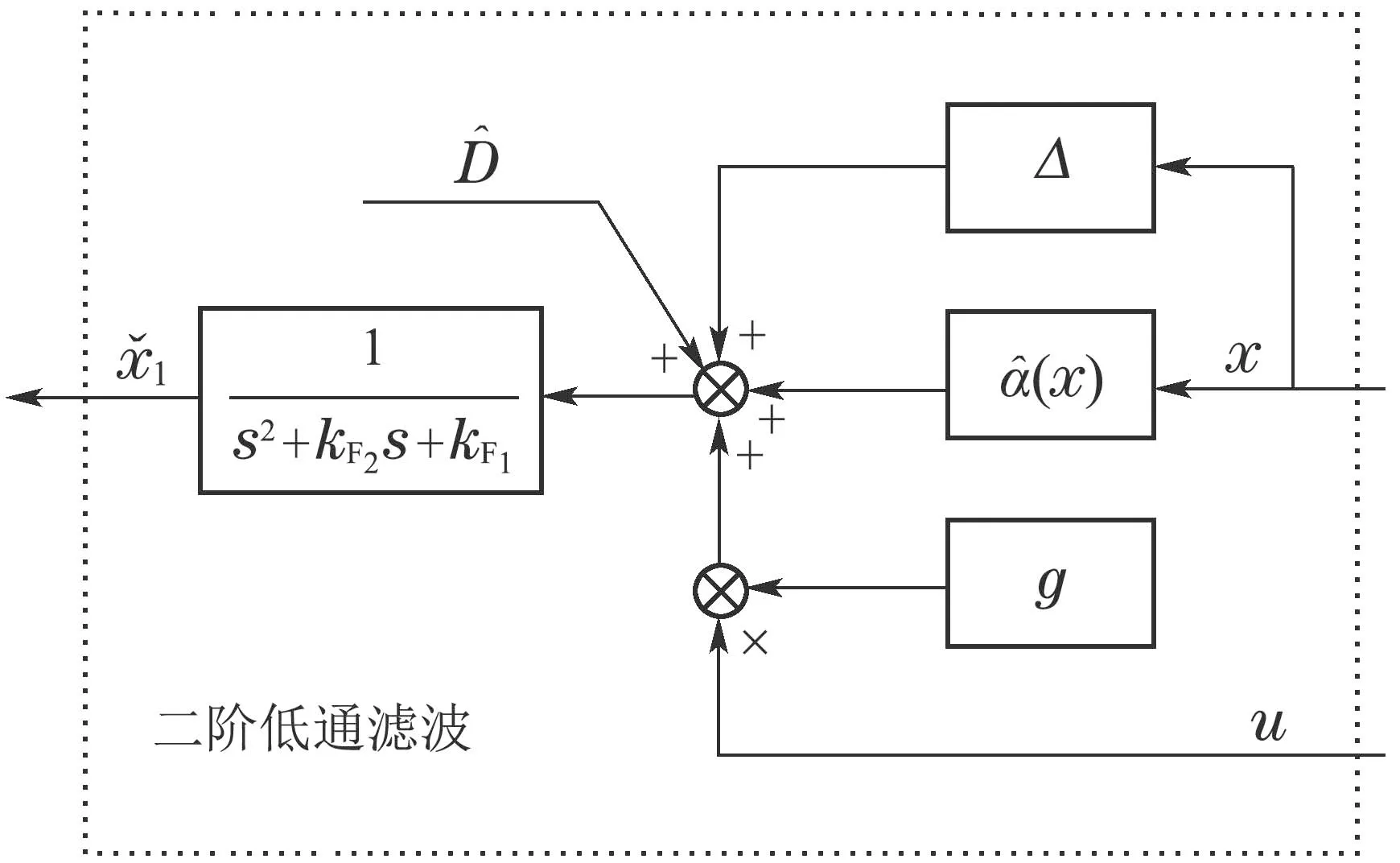
图3 二阶低通滤波辨识模型Fig.3 Identification model with second-order low-pass filter

结合式(11)(15)–(16),建模误差动态方程为

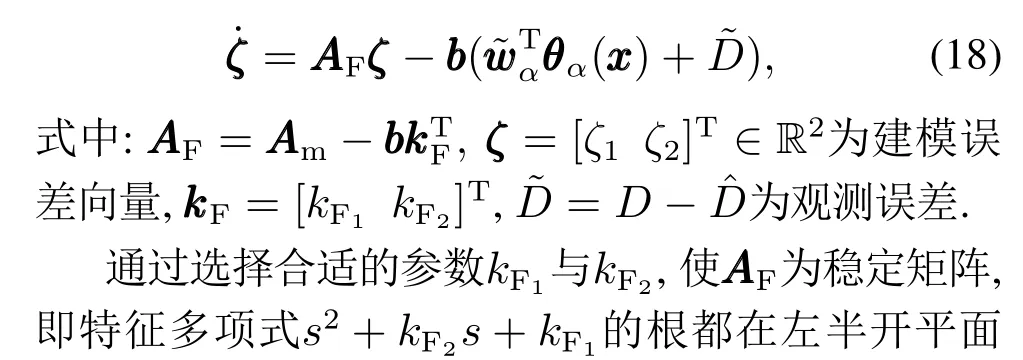
3.2 干扰观测器设计

3.3 控制律设计与系统稳定性分析

结合以上提出的复合神经网络自适应学习率与干扰观测器,式(5)应改取为以下反馈控制律:

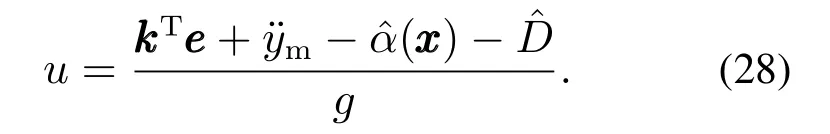
控制结构原理图如图4所示.将式(28)代入式(4),可得跟踪误差动态方程

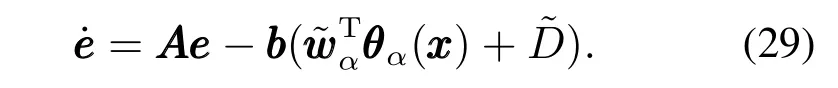
图4 控制器原理图Fig.4 The diagram of proposed controller

定理1对于SbW系统(4),在复合自适应学习率(20),干扰观测器(24)和控制律(28)的作用下,可以实现闭环系统跟踪误差一致最终有界,且闭环系统的跟踪误差e收敛于以下紧集Ωe:

选择合适的参数σ1,ks,lα和矩阵A,AF,Q,QF使得紧集Ωe足够小,可保证前轮转角跟随参考转角信号.根据式(33)可知,V的收敛速度与参数ϱ0有关,通过选取合适的矩阵A,AF,Q,QF以及参数pa可以提高V收敛于的速度,同时也提高了跟踪误差e的收敛速度.证毕.

注1当复合自适应学习率(20)满足第2种情况下,可以得到

4 仿真与实验分析

4.1 仿真参数设定与结果分析

步骤1控制器参数选择.

选择如下RBFNN结构:

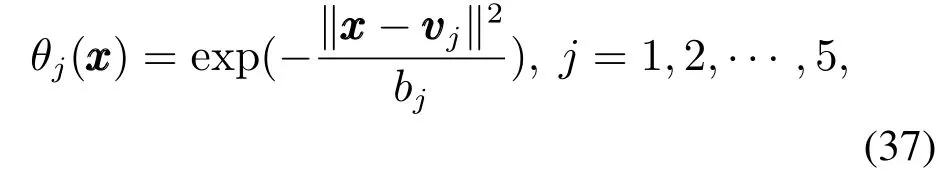
式中bj=0.5为网络的基宽.对于网络基宽的选取,如果基宽取值太大,网络对样本中的局部信息无法辨识;相反,如果基宽值过小,则对样本的整体信息可能丢失.根据仿真与实验的效果来看,本文选取的网络基宽为bj=0.5时仿真与实验效果最佳.另外,按照文献[14]所述,在所规定的RBFNN输入变量区域内均匀选取中心值可使得RBFNN能够一致逼近光滑的函数,这里RBFNN中心值的选取将采用此方式.隐藏层个数取j=5,在RBFNN输入变量经过归一化后中心值均匀分布在[0,1]×[0,1].vvvj为网络的中心值向量,

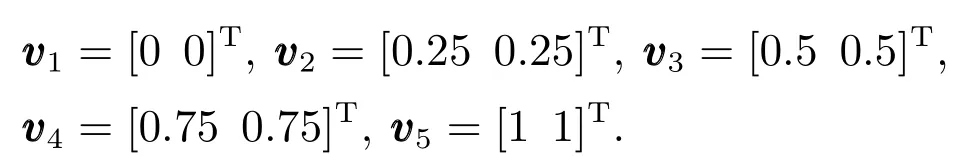
控制器(28)中的设计参数按照试凑法的方式选取为

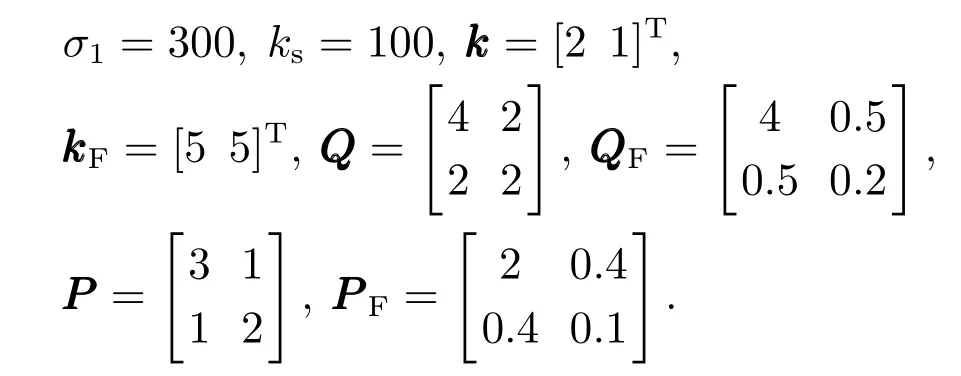
系统模型详细参数见表1.

表1 SbW系统模型参数Table 1 The parameters of SbW system

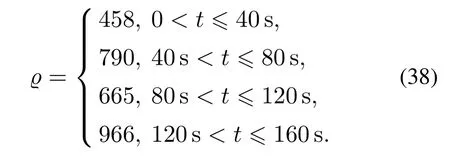
步骤2工况选择与仿真对比分析.

轮胎回正力矩系数设置如下:

对比控制器选取如下:

1) 为验证本文所提出的 (composite adaptive neural network–2,CANN–2)控制器的性能,选取比例积分微分 (proportional-integral-derivative,PID) 控制器作为对比:

其中:kP=1700,kI=700,kD=35.

2) 为验证所提出复合自适应学习率的优越性,选取传统自适应神经网络控制器(neural network,NN),即自适应学习率仅由跟踪误差调节,表示如下:

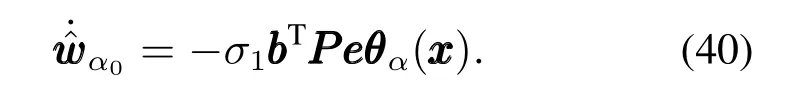
干扰观测器设计为

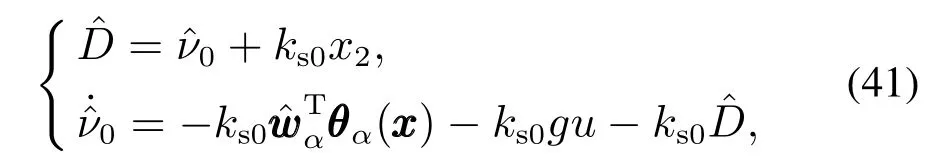
其中ks0=10.

3) 为验证 CANN–2 控制器处理测量噪声的能力,选取一 阶低通 滤波辨 识模型 复合自 适应神经网络控制器 (composite adaptive neural network–1,CANN–1)[29],辨识模型表示如下:

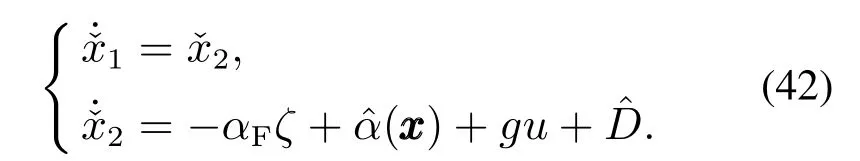
自适应学习率设计为

干扰观测器设计为

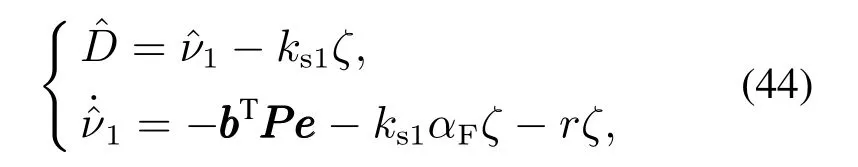
其中:αF=10,r=0.4,ks1=10.

在第 1 组对比仿真中,设置前轮转角期望信号为ym(t)=0.4sin(0.4πt) rad,仿真结果对比如图5所示.图5(a)为各控制器的输入.跟踪误差性能如图5(b)所示,可以看出4 种控制器均能有效地控制前轮转角信号,但在CANN–2控制器下的跟踪误差具有更快的收敛速度和更小的幅值.与固定增益的PID控制器相比,CANN–2控制器在变化的路况中能够保持较小的跟踪误差.与仅由单误差调节的NN控制器相比,复合调节的CANN–2控制器能够更精确地逼近系统不确定动态.为了验证CANN–2控制器处理测量噪声的能力,在二阶低通滤波辨识模型和一阶低通滤波辨识模型中加入正弦噪声信 号yH=0.5sin(100t).与CANN–1控制器相比,CANN–2控制器具有更强的噪声抑制效果.图5(c)为复合干扰的估计值,说明干扰观测器能够有效的补偿外界干扰.图5(d)为各控制器下的均方根差(root mean square error,RMSE)大 小,验证了所提出的控制器在不同路况下有较好的控制性能.

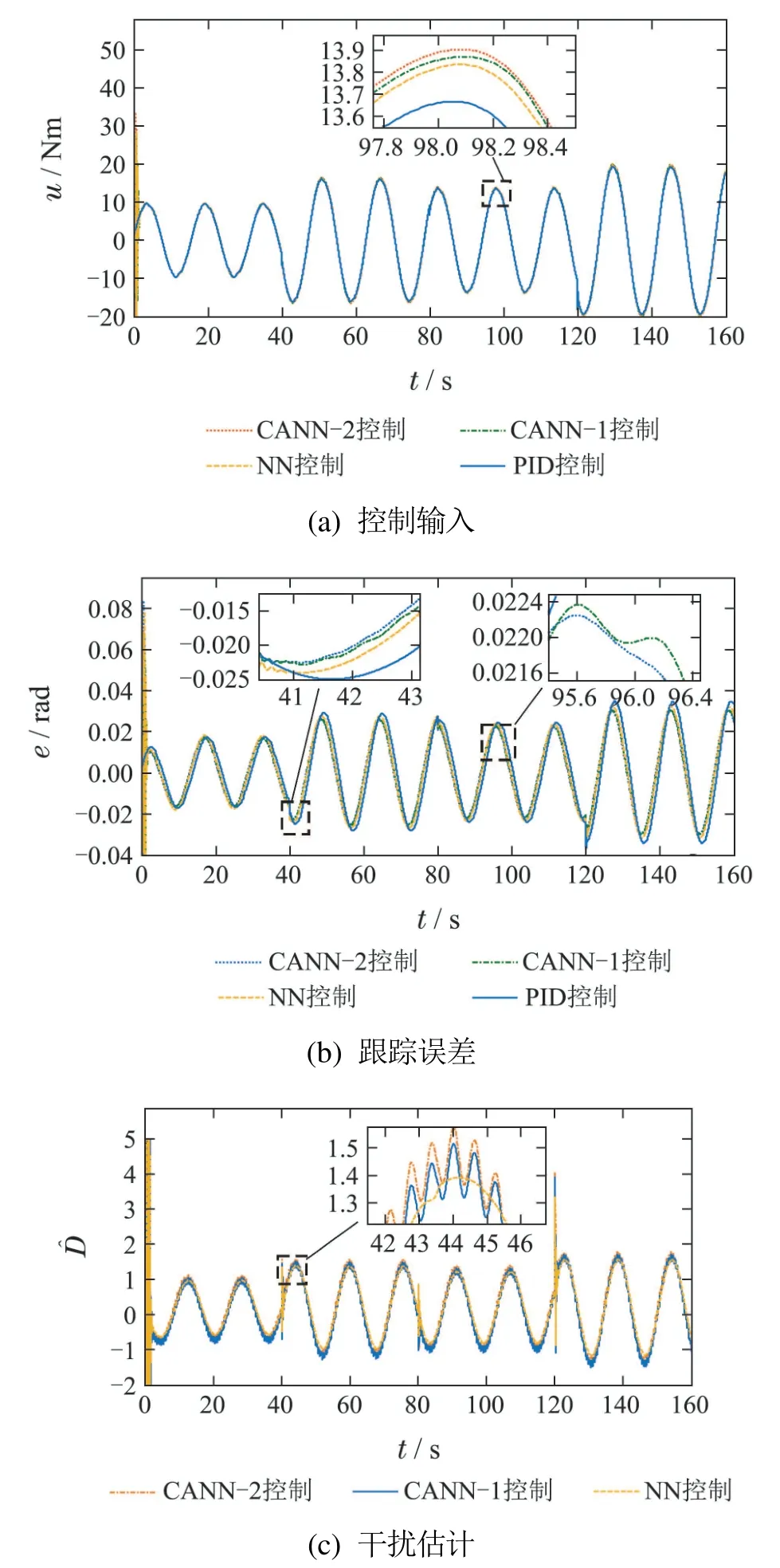
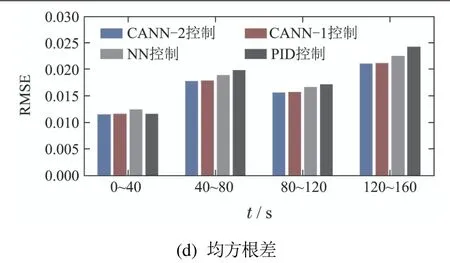
图5 仿真对比结果1Fig.5 The first group of compared simulation results

为了更加直观地体现在所提控制方法下的跟踪误差收敛速度的提升,本文增加了第2组仿真对比验证,仿真结果对比如图6所示.图6(a)为前轮 转角参考角度.图6(b)为各控制器的跟踪误差性能曲线,可以看出在4种控制器下的前轮转角均能有效地跟踪参考输入信号.从局部放大图中可以看出,在CANN–2控制器下的跟踪误差最先收敛到较小的零域内,具有更快的收敛速度.与仅由跟踪误差调节的NN控制器相比,CANN–2控制器在跟踪误差收敛速度调节上具有明显的优势.从图6(c)所展示的干扰估计结果来看,说明本文设计的干扰观测器能够将复合干扰有效地估计出来,这也为控制器的成功补偿提供了条件.图6(d)为跟踪 误差的均方根差柱状图.从表2中可以看出CANN–2控制器在仿真中的跟踪误差具有最小的标准差与方差,可以看出本文所提出控制器具有较好的控制性能.

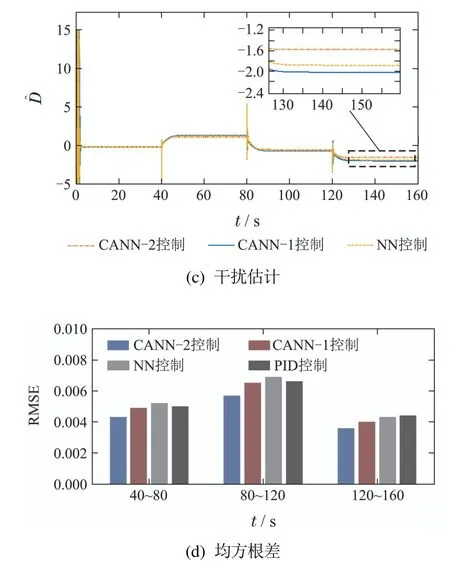
图6 仿真对比结果2Fig.6 The second group of compared simulation results

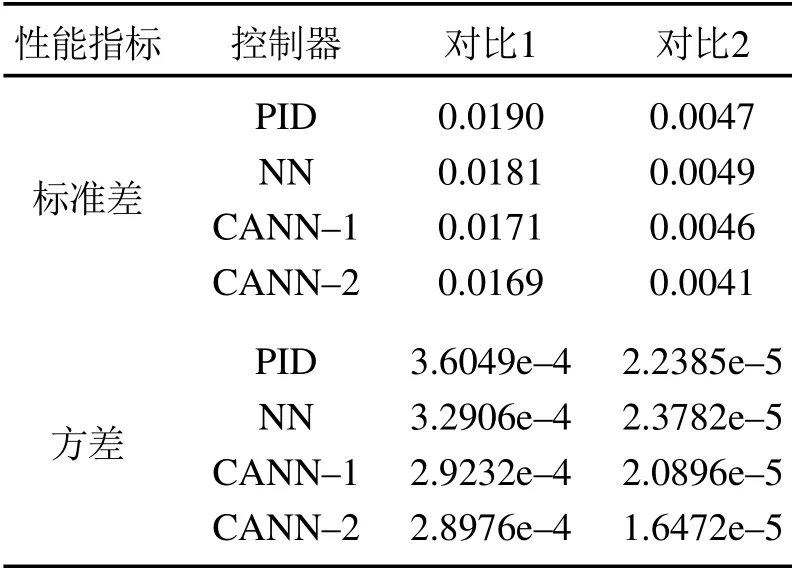
表2 仿真数据对比Table 2 The comparative data in simulation

4.2 基于SbW硬件在环平台的跟踪实验验证

步骤1建立实验平台.

为了进一步验证所提出控制器在实际中的控制性能,本文搭建了SbW系统硬件在环实验平台,如图7所示.实验设备主要包括控制器(dSPACE)、电机驱动器(XINJE–DS2–20P7)、转向电机(XINJE–MS80ST)、线性传感器(KTR11–10)、减速器、转向执行器以及上位机组成.控制算法在 Simulink 编译为 C 代码后下载到dSPACE控制器中,同时I/O模块接收传感器测量的前轮转角信号.经过控制算法运算后产生的控制转矩信号,通过RS485总线发送给电机驱动器.

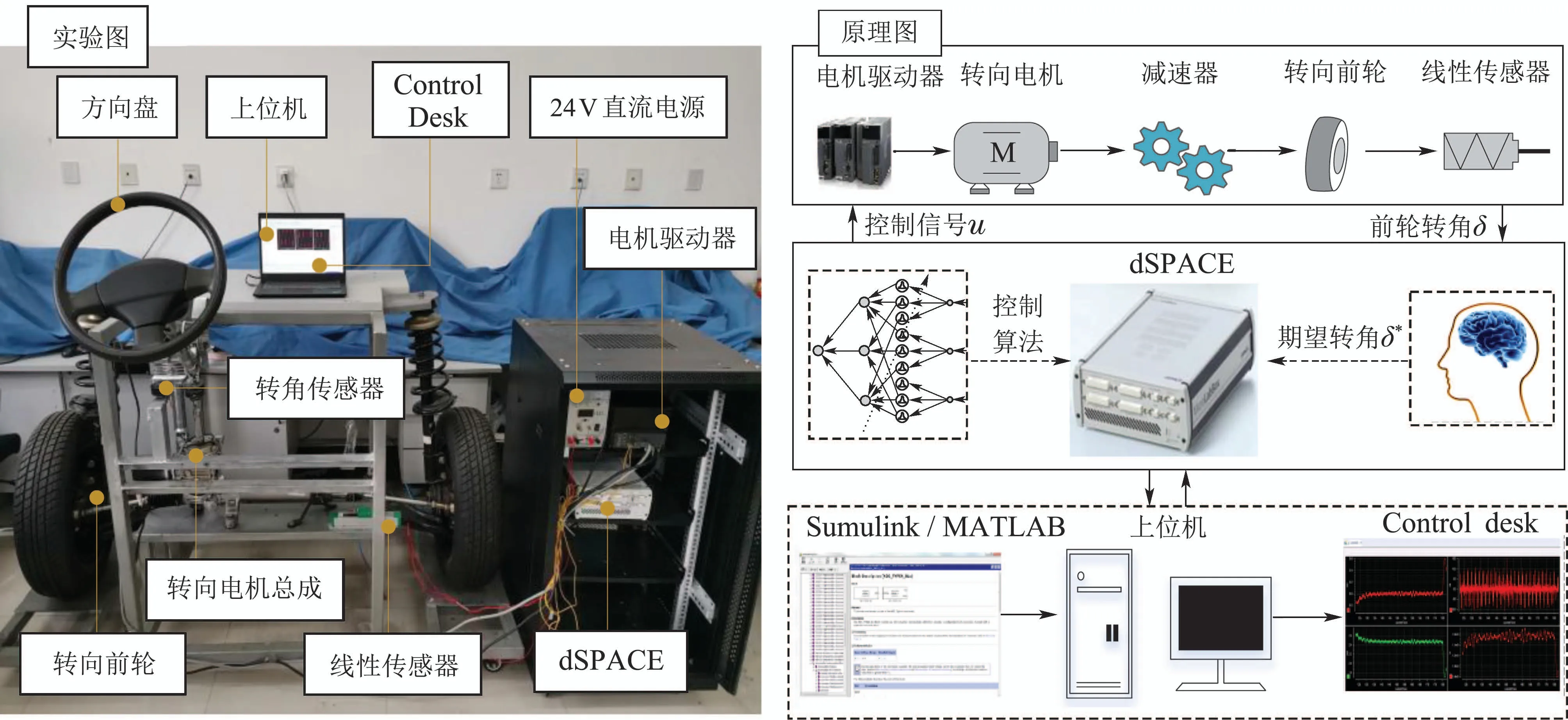
图7 SbW系统硬件在环实验平台Fig.7 The hardware-in-loop experimental platform of SbW system

最后驱动器根据控制信号驱动转向电机实现前轮转向,完成驾驶员的转向意图.所有信号的监视与标定均在上位机软件ControlDesk实现,dSPACE控制器与上位机通过Ethernet进行通讯.

步骤2实验对比分析.

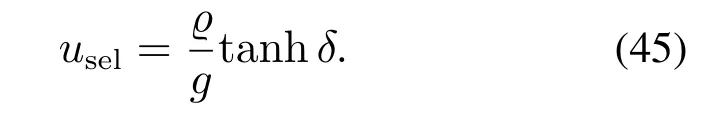
由于实验条件的限制,不能为SbW系统提供行驶速度,因此前轮在实际转向的过程中不会受到回正力矩的影响.为了验证所提出控制器在不同工况下的优越性,在 控制器u中加入 如下信号来模拟前轮转向过程中受到的回正力矩:实验对比结果如图8所示.图8(a)为在控制器下的控制输入转矩曲线.跟踪误差性能曲线如图8(b)所示,从局部放大视图可以看出在不同的路况下CANN–2控制器具有更小的跟踪误差.图8(c)为复合干扰的估计值,说明在实际环境中干 扰观测 器也能够有效的补偿外界干扰的影响.各控制器下RMSE性能指标如图8(d),其中所提出的控制器具有更好的控制效果.

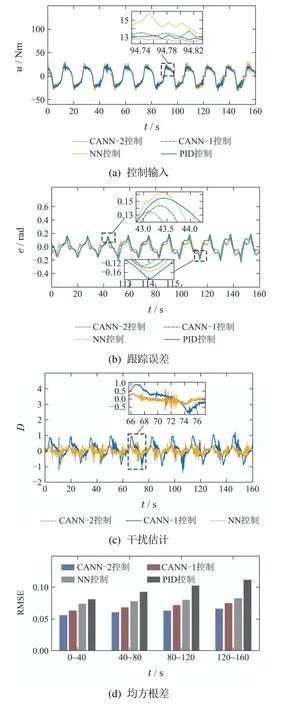
图8 实验结果对比1Fig.8 The first group of compared experiment results

为了进一步验证所提控制器在硬件在环实验中对噪声的衰减效果,笔者在一阶低通滤波辨识模型和二阶低通滤波辨识模型分别加入相同的正弦噪声信号,实验结果如图9所 示.CANN–1和CANN–2的控制 输入如图9(a)所示,可以看出所提出控制器的控 制输入具有较小的波动.图9(b)展示了两种控制器在正弦噪声环境下的跟踪误差曲线,从图中可以看出CANN–2控制器作用下的跟踪误差较为平滑,说明了CANN–2控制器具有更强的噪声抑制效果.表3为所有控制器的实验数据对比,可以看出CANN–2控制器的跟踪误差具有最小的标准差与方差.以上结果表明了在SbW系统中采用所提出控制方法的实用性与优越性.

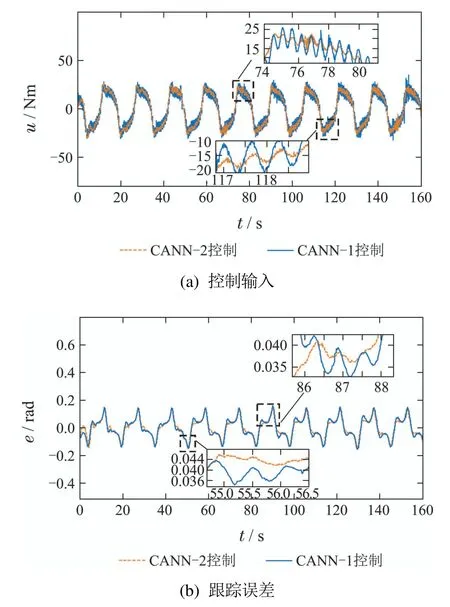
图9 实验结果对比2Fig.9 The second group of compared experiment results

表3 实验数据对比Table 3 The comparative data in experiment

注3在实际SbW系统中,传感器等检测设备会受到噪声干扰的影响,但由于外界噪声干扰具有有限的能量,所以噪声干扰的幅值是有限的.同时,在保证检测设备不发生故障的情况下,噪声干扰不会突然变化[31–32].所以在硬件在环实验中所涉及的噪声干扰满足假设1.

5 结论

本文提出了一种基于干扰观测器的复合自适应神经网络跟踪控制策略,以解决SbW系统中存在不确定动态与外界干扰的问题并实现对前轮转角 的有效 跟踪控制.通过设计二阶低通滤波辨识模型构造复合自适应学习率,其中自适应参数由建模误差向量和跟踪误差共同调节,不但有效地衰减了测量噪声还加快了系统跟踪误差的收敛速度.通过设计干扰观测器来估计系统受到的复合干扰,在输入通道中将观测出的干扰值抵消,提高了系统抗干扰能力.最后,Lyapunov稳定性理论证明了系统跟踪误差一致最终有界.不同工况下的仿真和实验结果表明了该控制器在SbW系 统中的有效性和优越性.本文未来的研究中还有许多工作要做,例如结合预设性能函数实现对跟踪误差收敛速度进行定量调节;当SbW系统中检测设备发生故障时,结合干扰观测器技术实现对系统的容错控制.

附录

由式(A10)可知与传统自适应学习率相比,采用复合自适应学习率会产生与建模误差有关的附加项,加快了李雅普诺夫函数V的下降速度,即提高了跟踪误差收敛于紧集的速度.