限定尺寸的无线电能传输线圈优化设计
张智娟, 郑龙飞, 杨 瑞
(华北电力大学电气与电子工程学院, 保定 071003)
无线电能传输技术(wireless power transfer, WPT)是指电源和负载之间的电能转换主要以电磁波的形式进行而不需要物理导线的连接,和传统的传输方式相比,因更加安全、便捷、灵活、适应性强的特点而备受关注[1]。目前WPT技术可以分为感应式、磁耦合谐振式和微波式无线电能传输三种形式。其中微波式无线电能传输距离虽远,但效率却极低。感应式和磁耦合谐振式无线电能传输技术都能以高效率完成电能的传输,磁耦合谐振式因具有较远的传输距离而占据了更多优势成为该领域研究的焦点[2]。
传输效率作为WPT系统的重要指标,一直以来都是研究和应用的重点,而线圈作为WPT系统的重要组成部分对传输性能有至关重要的作用,曾玉凤等[3]介绍了线圈常用的设计方法,总结了各方法的适用范围,提出了设计具有高品质因数和均匀磁场的线圈是线圈优化设计的方向。研究表明对传输线圈的匝数、内径、线径等参数进行优化能有效提升系统传输效率[4]。其中线圈匝数的影响最大,其次是线圈内径,最后是匝间距和线径[5]。刘国波等[6]通过为线圈增加磁芯来增大线圈的互感和耦合系数的方法提升了系统的传输效率,在450 kHz的工作频率和40 cm的传输距离下,系统能够获得80%左右的传输效率。在线圈类型方面,文献[7]优化设计了一种新型线圈,在具有水平偏移的情况下和平板型线圈相比具有更好的互感和耦合系数并且体积比平板型线圈减小了40%。在线圈结构和匝数方面,文献[8]通过有限元分析,在谐振频率6.78 MHz下对医疗植入式传输线圈进行了优化,在5 cm距离内可以获得40%以上的稳定功率传输效率。上述文献采用了不同的线圈优化方法提升了系统传输性能,但尚未对线圈参数受限时系统的传输性能进行研究。
首先,从理论上研究双线圈串串拓扑结构的等效电路模型和传输线圈模型参数,探究优化平面螺旋线圈的主要影响因素;其次,利用ANSYS软件以品质因数为衡量标准,对传输线圈进行研究和设计,找到尺寸约束下线圈的最优匝数和匝间距;最后,基于磁耦合谐振式进行仿真实验,根据理论和仿真的优化结果绕制线圈,并通过仿真和实验对理论研究和设计进行验证。
1 无线电能传输系统分析
WPT系统主要由发射回路和接收回路两部分组成,发射回路主要包括高频交流电源、发射线圈和谐振电容,接收回路主要包括接收线圈和谐振电容、整流滤波稳压电路、负载等。为了便于分析,将磁耦合谐振WPT系统电路进行简化,得到的电路模型如图1所示。
设图1中发射端电源电压u0已知,电源角频率为ω,则电路谐振时满足
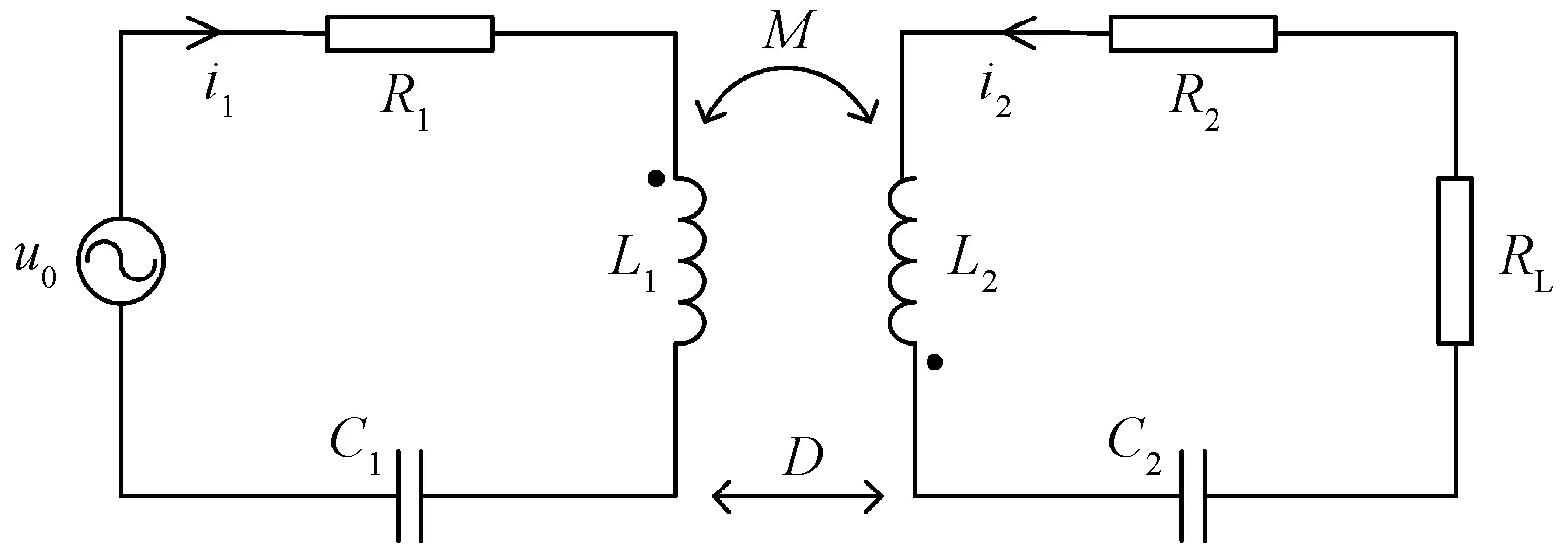
u0为电源电压;RL为负载电阻;R1、R2为线圈的等效电阻;L1、L2、C1、C2分别为原边、副边线圈的电感和谐振电容;M为两线圈之间互感;D为两线圈间距离
(1)
将发射和接收回路的阻抗分别记为Z1、Z2,电路谐振时有Z1=R1,Z2=R2+RL。结合基尔霍夫电路定律求得系统的输入功率为
(2)
接收回路负载RL上的输出功率为
(3)
式中:U0、I1、I2分别为u0、i1、i2的有效值。传输效率为
(4)
由式(4)得到,传输效率η是关于系统谐振角频率ω、传输线圈互感M、负载RL以及传输线圈的等效电阻R1、R2的多变量函数,线圈完全对称时,设电感L=L1=L2,电容C=C1=C2,电阻R=R1=R2,对传输效率公式进行进一步整理。
根据互感和品质因数的表达式:M=k(L1L2)1/2,Q=ωL/R,再令x=RL/R,传输效率可以化为关于x的函数[9]
(5)
计算得到当x=(1+k2Q2)1/2,该函数能取得最大值,此时RL=R(1+k2Q2)1/2,即负载最优时的传输效率为
(6)
从式(6)可以看出,传输效率大小和线圈间的耦合系数和品质因数有关,为了更加直观地了解传输效率、耦合系数和品质因数之间的关系,利用MATLAB绘图得到品质因数与耦合系数的乘积和效率的关系曲线图如图2所示,由图2可以看到,在负载为最优的条件下,传输效率的值随着耦合系数k和品质因数Q乘积的增大而增大,由此可以通过提高耦合系数k和品质因数Q来提高传输效率,也就是改变线圈电感L1、L2以及电阻R1、R2来得到更高的传输效率,即通过提高线圈电感和减小线圈电阻得到更高的效率。
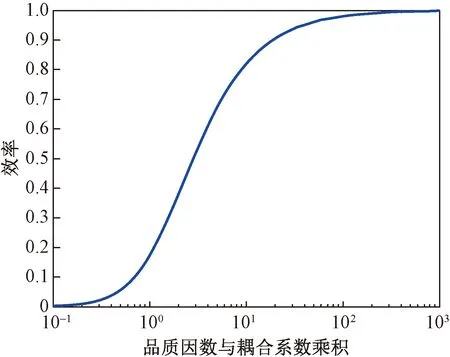
图2 品质因数与耦合系数乘积和效率的关系曲线Fig.2 The relationship curve between the efficiency and product of the quality factor and the coupling coefficient
2 传输线圈影响因素优化分析
通过前文的分析得到线圈间耦合系数、线圈电感和电阻是传输效率的主要影响因素。对于手机和汽车等有体积限制的充电设备,平面螺旋线圈因其紧凑的结构特点和近距离传输时能够获得较大的磁场而成为大多数无线电能传输理想的选择,所以,以平面螺旋线圈为对象研究影响电感、耦合系数和电阻的因素。
2.1 电感和耦合系数的影响因素
线圈电感值以及互感和耦合系数主要和线圈的结构有关,此外,互感和耦合系数还与线圈间的距离有关,平面螺旋线圈其结构模型如图3所示。
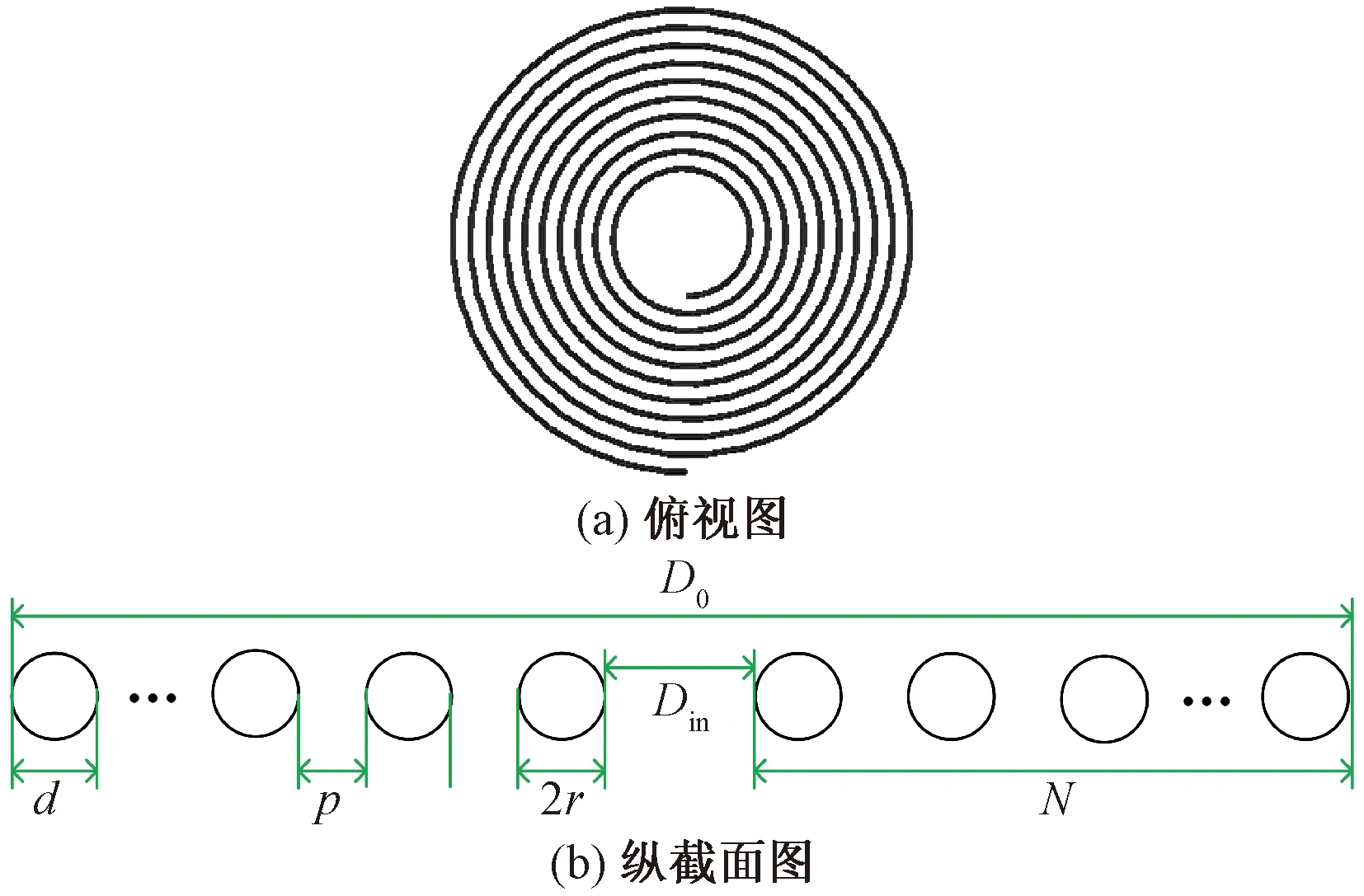
图3 平面螺旋线圈结构模型Fig.3 Structure model of plane spiral coil
平面螺旋线圈自感L和互感M的计算公式[10]为
(7)
(8)
式中:N为平面螺旋线圈匝数;N1、N2为发射、接收线圈匝数;D0为线圈外直径,m;Din为线圈内直径,m;D为两线圈间距离,m;d为线圈导线直径,m;r为线圈导线半径,m;p为线圈匝间距,m;μ0为真空磁导率,H/m。
为了便于分析各变量之间的关系,现对线圈尺寸进行约束,设线圈外直径为10 cm,导线线径为1 mm,发射接收线圈参数相同,得到线圈电感与匝间距和匝数之间的关系如图4所示。
由图4可知,在匝间距确定的情况下,电感值随匝数的增大呈上升趋势;在匝数一定时,匝间距越小电感值越大,那在线圈尺寸约束的情况下线圈匝间距越小,匝数越多对应的电感越大。再由式(7)和式(8)以及互感M=k(L1L2)1/2得到耦合系数和线圈匝数、传输距离的关系如图5所示。
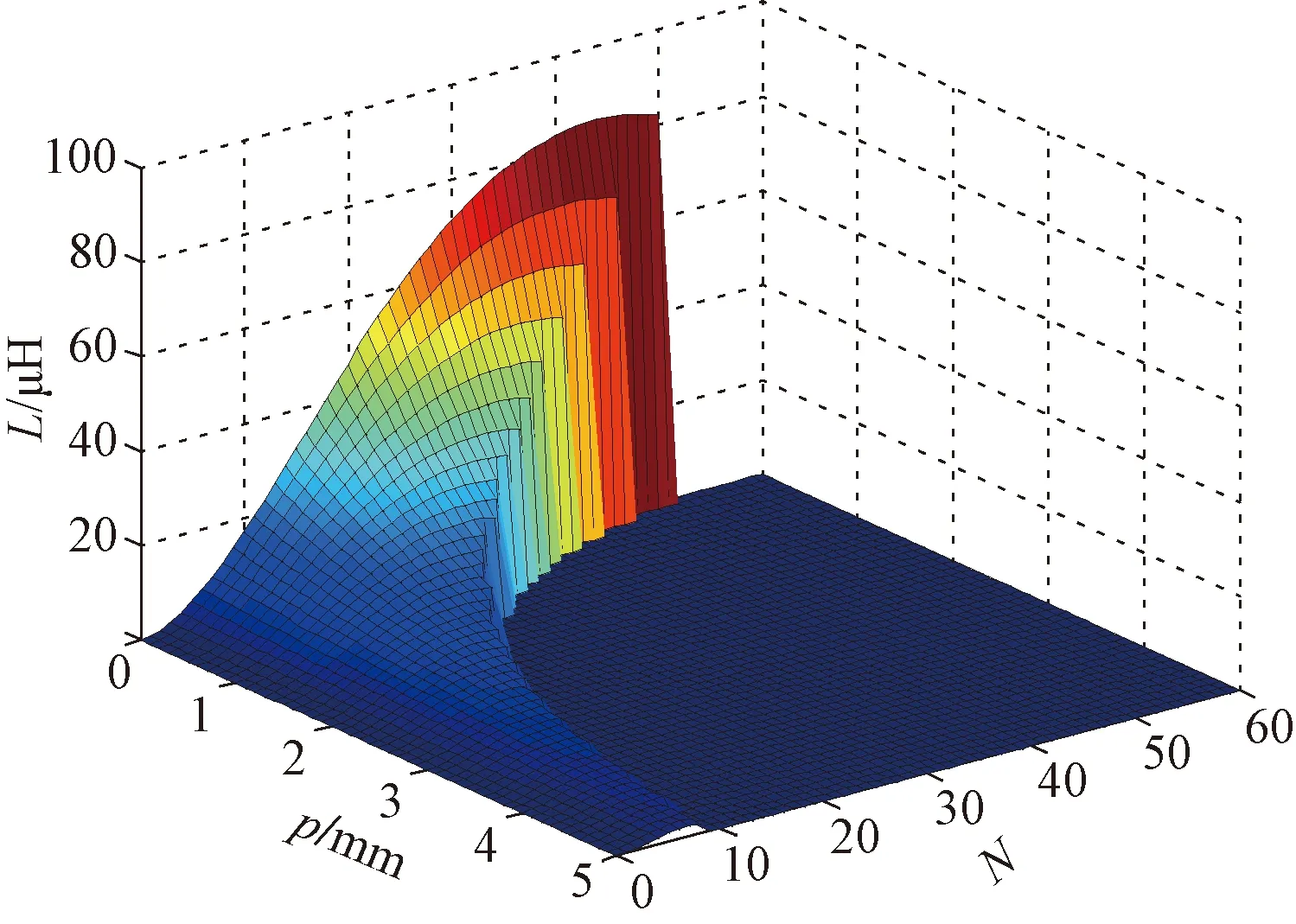
图4 电感与匝间距和匝数之间的关系Fig.4 Relationship between inductors and spacing and number of turns
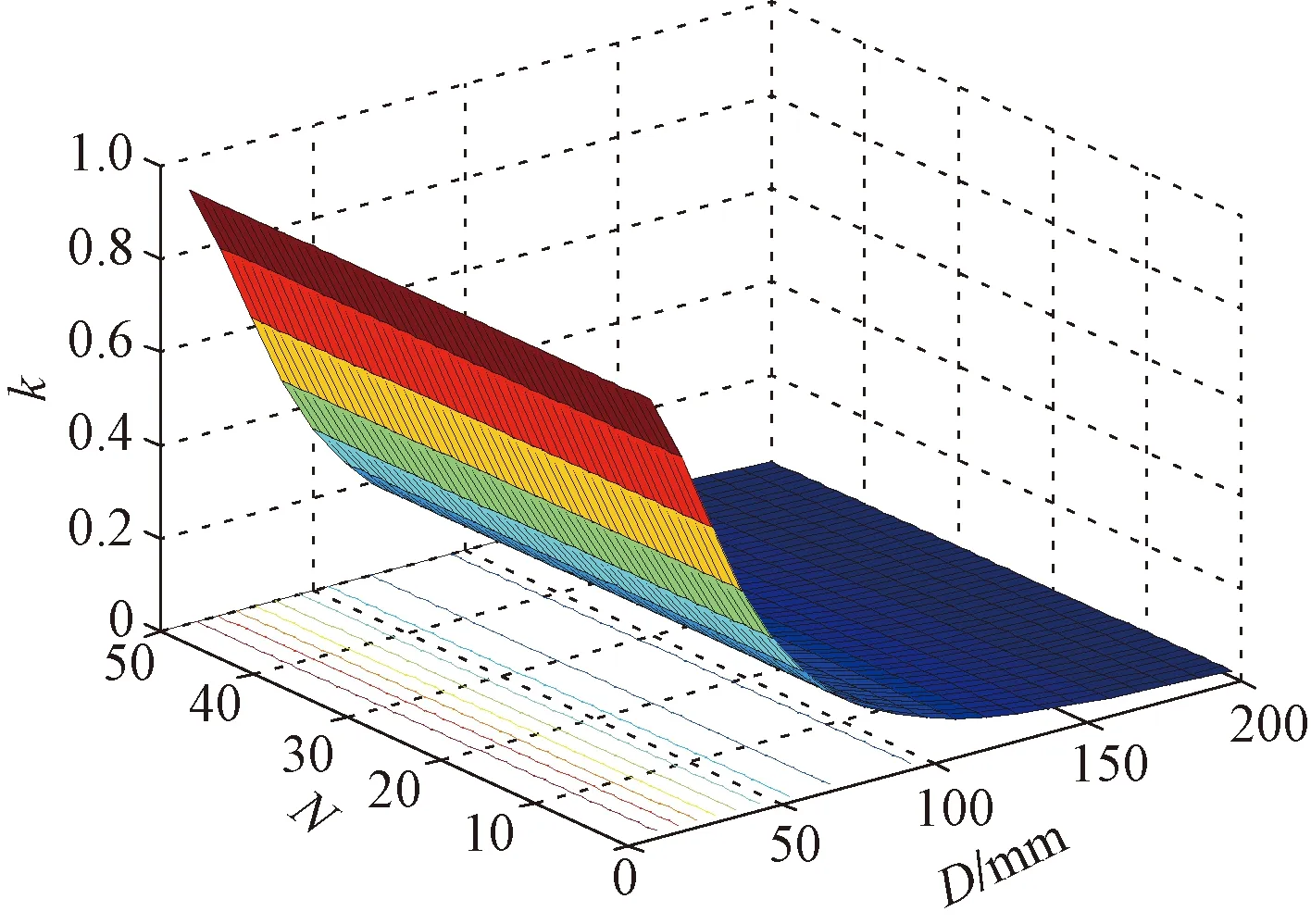
图5 耦合系数与匝数和传输距离之间的关系Fig.5 Relationship between coupling coefficients and number of turns and transmission distance
从图5的耦合系数和线圈匝数、传输距离的三维图可以看出,在线圈尺寸受限时,耦合系数随传输距离的增大不断衰减,并且由图5中的等势线可知匝数对耦合系数的影响很小,结合图2的分析结果可知品质因数是效率的主要影响因素。
2.2 电阻影响因素
电阻的影响因素主要是趋肤效应和邻近效应,两者在频率越高时越明显,而且邻近效应还与导体之间的距离有关,从而影响线圈匝间距的选择。在系统谐振频率较高时,因为趋肤效应和邻近效应的存在,线圈的电阻很难用具体的公式来计算,而通过有限元的建模分析可以得到较为准确的结果。为了更加直观地了解电阻的影响因素,利用ANSYS仿真软件中的电磁场分析模块(Maxwell)对通电导线进行仿真分析。导线线径为1 mm,频率为1 MHz时在不同间距下的电流密度仿真图如图6所示。
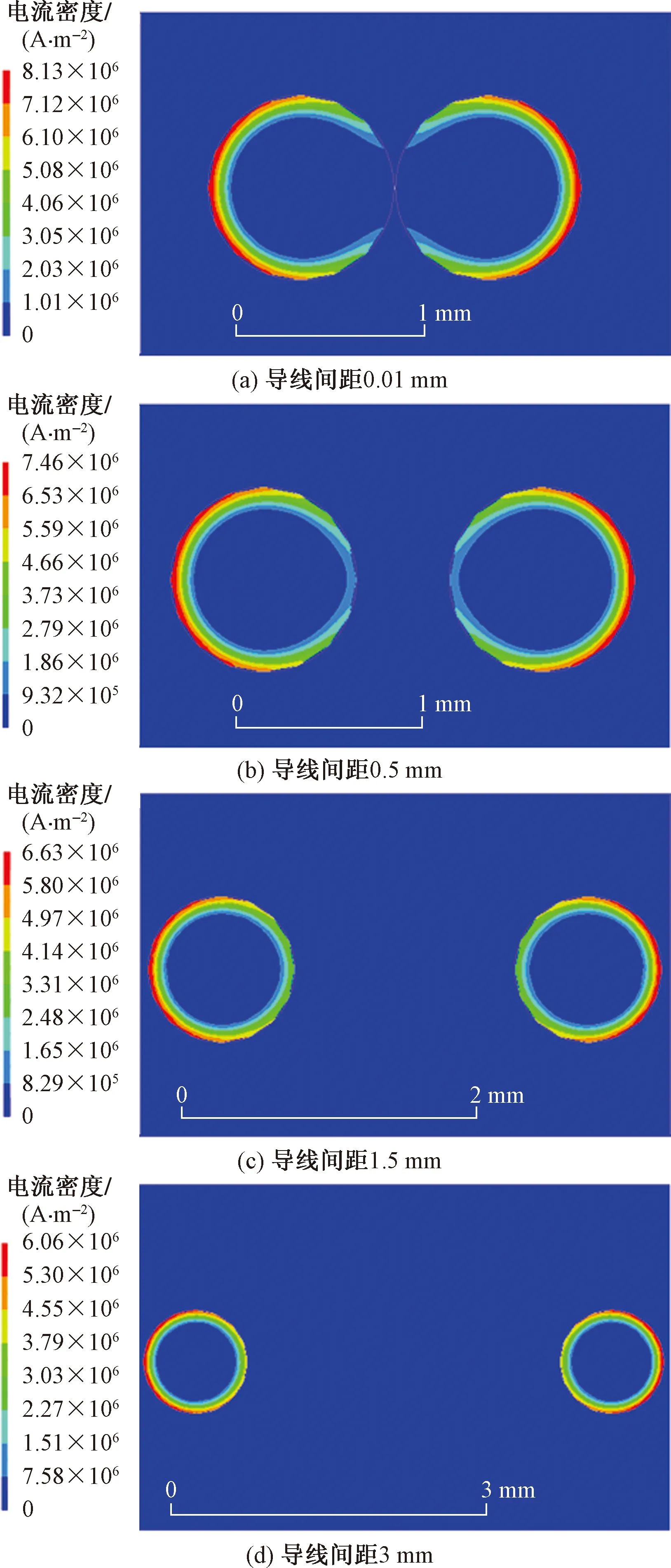
图6 不同间距下的电流密度图Fig.6 Current density map at different spacing
通过上面的分析可知,线圈的匝间距越大,导体中的电流越趋于均匀,对线圈交流电阻的影响就越小。但匝间距越大就意味着相同线圈尺寸、相同导线半径的情况下线圈的匝数就越少,而线圈的自感随匝数的增加而增大。所以要在尺寸约束的条件下得到较大的传输效率,就要找到一个匝间距,对应一个匝数,从而使得内阻较小而电感较大,使得这时候的品质因数Q=ωL/R最大。由上文分析的结论可知,传输效率随着耦合系数和品质因数的乘积的增大而增大,在尺寸约束时,不同匝数对应的耦合系数几乎不变,所以在限制尺寸时品质因数的大小将直接决定线圈的传输性能。
3 参数优化设计仿真研究
要找到最优的线圈匝间距和匝数需要大量的数据进行分析,利用ANSYS仿真软件中的电磁场分析模块Maxwell对线圈进行建模仿真,在Maxwell的涡流场(eddy current)求解模式下建立三维平面螺旋线圈模型,设置电流激励,网格剖分后经过有限元分析和矩阵参数的结果处理得到不同约束尺寸线圈最大品质因数对应的匝间距和匝数。
3.1 线圈模型参数优化
考虑到实验条件和仿真时对内存的要求,以尺寸交叉设置的方法进行仿真。仿真参数设置为铜导线线径1 mm,频率1 MHz,线圈尺寸内外半径约束为30~40 mm,40~50 mm,30~50 mm。平面螺旋线圈模型示意图如图7所示,仿真得到的线圈参数如表1~表3所示。

图7 平面螺旋线圈仿真模型Fig.7 Plane spiral coil model
由表1~表3可知,线圈的匝间距越大,线圈的交流电阻越小,相同线圈尺寸、相同导线半径的情况下线圈的匝数越少,线圈的自感值也就越小,而此时的品质因数Q的变化趋势却是先增大后减小的,也就是存在一个匝间距,对应一个匝数能使品质因数Q取得最大值,由此可见仿真和理论分析的结果是一致的。

表1 尺寸限制为内半径30 mm、外半径50 mm的线圈参数Table 1 Coil Parameters under size limit to 30 mm inner radius and 50 mm outer radius
由表1和表2可知,在内半径和匝间距相同的情况下,外半径大,即匝数多,对应的电感值大,电阻值大,品质因数高。由表2和表3可知,在相同的匝数和匝间距的情况下,线圈平均半径大的电感值大,品质因数高。由表1~表3可知,不同线圈尺寸对应的最优匝间距是相同的,均为0.42 mm。在导线半径为0.5 mm,频率为1 MHz,内外半径约束时,就可以根据内外半径的差值和匝间距以及导线半径计算得到对应的匝数,从而对线圈进行绕制。
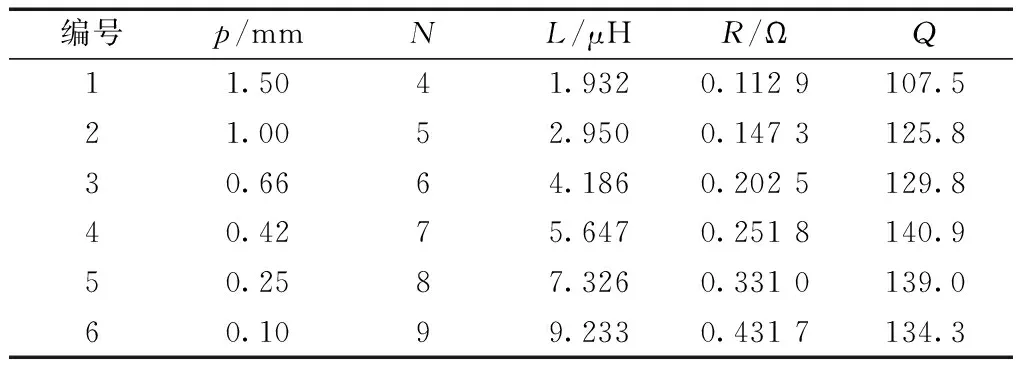
表2 尺寸限制为内半径30 mm、外半径40 mm的线圈参数Table 2 Coil parameters under size limit to 30 mm inner radius and 40 mm outer radius

表3 尺寸限制为内半径40 mm、外半径50 mm的线圈参数Table 3 Coil parameters under size limit to 40 mm inner radius and 50 mm outer radius
3.2 联合仿真分析
仿真选取线圈尺寸为30~50 mm,建立线圈模型匝数14、匝间距0.42 mm为优化组并编号C-2,匝数18、匝间距0.1 mm和匝数10、匝间距1 mm为对照组并分别编号C-1和C-3,仿真验证以不同方式绕制得到的不同品质因数的线圈在不同距离下的传输性能。仿真信号源峰峰值为10 V,内阻50 Ω,频率1 MHz,其他参数如表4所示。
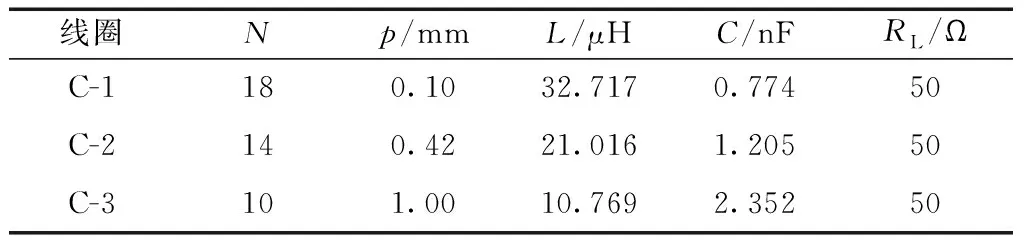
表4 系统仿真参数值Table 4 Parameter values of the system simulation
仿真工具利用ANSYS仿真软件的电路分析模块Twin Builder,仿真时将Maxwell所设计的线圈模型导入Twin Builder模块中,由Maxwell和Twin Builder进行联合仿真,前者经过对线圈自感、互感和耦合系数等参数的有限元计算后通过状态空间方程输入Twin Builder模块进行电路仿真,仿真电路如图8所示。

图8 Maxwell和Twin Builder联合仿真电路图Fig.8 Maxwell and Twin Builder joint simulation circuit diagram
经过仿真得到不同线圈组在不同传输距离下的传输性能,通过对仿真数据的整理得到其传输效率和传输功率的结果如图9和图10所示。
从图9和图10可以明显地看到2号线圈(优化线圈组)在一定的传输范围内无论是在传输功率还是传输效率方面都具有明显的优势,2号优化线圈具有最高的传输效率,达到了0.97;其次是3号线圈,最高效率为0.88;最后是1号线圈,最高效率为0.86。2号线圈较1号线圈和3号线圈的传输效率分别提升了12.7%和10.2%。但1号线圈效率的稳定性略高于2号线圈,3号线圈最差,这主要是与各线圈的自感有关,自感值越小其传输效率的稳定性就相对较差,效率下降的趋势也就越快。
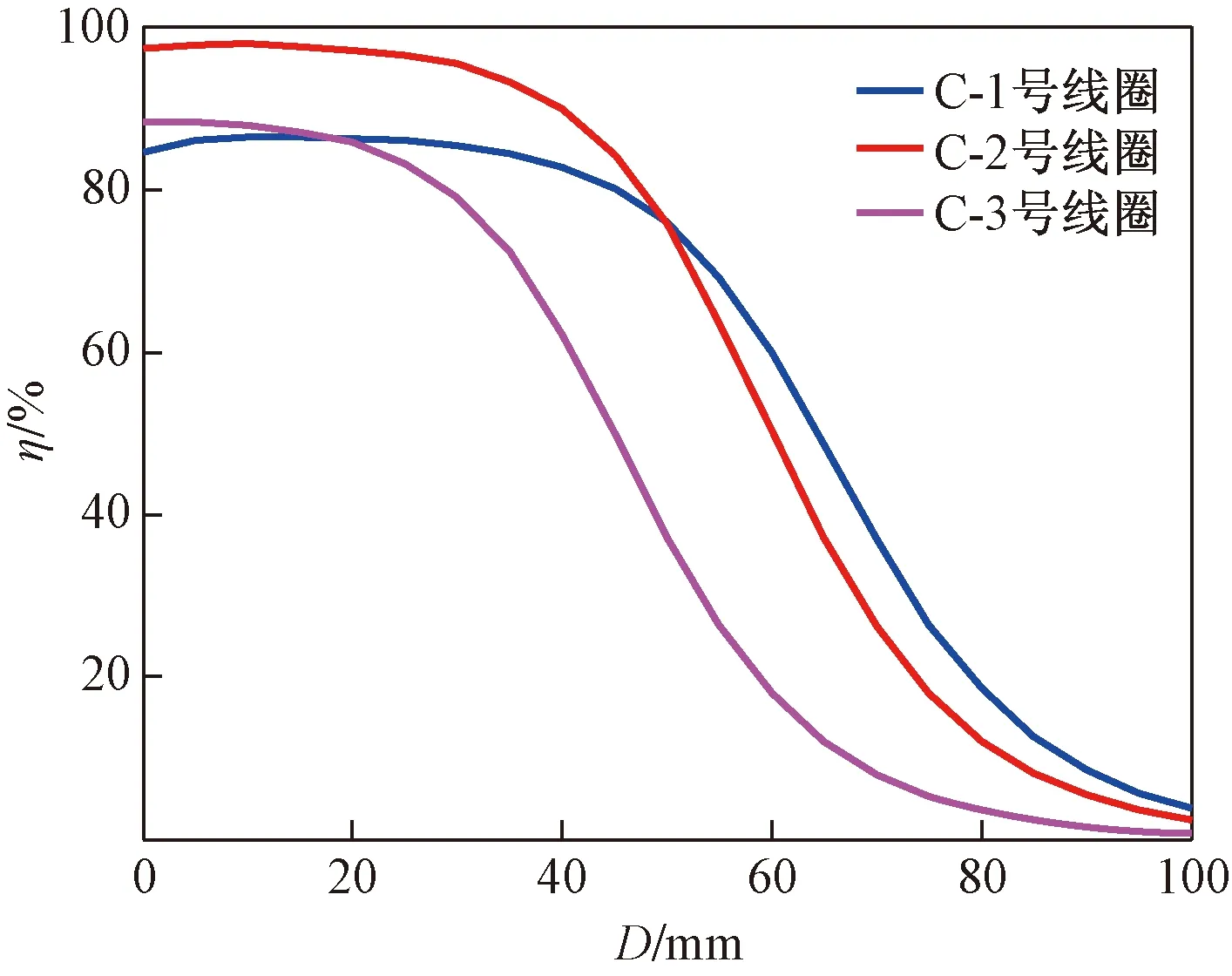
图9 仿真传输效率曲线Fig.9 The transmission efficiency curve of simulation

图10 仿真传输功率曲线Fig.10 The transmission power curve of simulation
4 实验验证
实验同仿真选取的线圈参数一致,选取线圈尺寸为30~50 mm,绕制线圈匝数14、匝间距0.42 mm为优化组并编号C′-2,匝数18、匝间距0.1 mm和匝数10、匝间距1 mm为对照组分别编号C′-1和C′-3,并对选取的线圈进行绕制。验证不同方式绕制的线圈在不同距离下的传输性能。实验信号源峰峰值为10 V,内阻50 Ω,频率1 MHz,其他参数如表5所示。

表5 系统实验参数值Table 5 Parameter values of the system experiment
根据仿真建立的实验装置如图11所示,信号发生器提供正弦波交流信号作用于发射线圈,接收线圈连接负载通过示波器来测量相关数值。

图11 实验装置Fig.11 Experimental equipment
经过实验得到各线圈组在不同传输距离下的传输性能,通过实验和仿真数据的整理得到其传输效率和传输功率的对比结果如图12和图13所示。

图12 实验和仿真传输效率曲线Fig.12 The transmission efficiency curve of experiment and simulation

图13 实验和仿真传输功率曲线Fig.13 The transmission power curve of experiment and simulation
从图12和图13可以看到,实验的传输效率曲线同仿真的传输效率曲线有很好的吻合性,C′-2号优化组线圈在一定的传输范围内传输功率和传输效率方面都明显优于C′-1号线圈和C′-3号线圈。优化线圈的最高传输效率是0.97,C′-1号线圈和C′-3号线圈的最高传输效率分别为0.85和0.87。C′-2号优化组线圈较C′-1号线圈和C′-3号线圈的传输效率分别提升了14.1%和11.4%。实验和仿真的传输功率曲线存在一定的误差,但整体的变化趋势一致,误差的主要原因是实验采用的信号源输出电压,线圈缠绕以及电容匹配存在一定的误差引起的。同仿真结果一样,受其自感等因素的影响,C′-3号线圈传输效率的下降趋势最快,C′-2号优化组线圈和C′-1号线圈效率下降较为平缓,所以在近距离传输时优化线圈组在传输功率和效率方面都有了明显的提升。
5 结论
在ANSYS仿真平台下详细研究了在系统谐振频率固定为1 MHz,导线线径为1 mm,线圈尺寸约束的条件下以品质因数为衡量标准的线圈优化设计的一种方法,从而得到了线圈在尺寸约束下的最佳缠绕方式,并通过实验验证了该方法的可行性,最终得到以下结论。
(1)在尺寸约束、选定系统频率和导线线径时,耦合系数变化曲线随传输距离不断衰减而和匝数无关,存在一个匝间距,对应一个匝数从而使得线圈的电感值较大而线圈内阻较小,此时线圈的品质因数最高,能在一定的传输范围内使系统的传输性能达到最佳状态。
(2)在谐振频率1 MHz,线径1 mm,线圈半径50 mm以内时的最佳匝间距为0.42 mm,最优匝数为14匝,优化后的线圈经过实验与对照组线圈相比,传输效率分别由0.85,0.87提高到了0.97,提升了14.1%和11.4%,优化线圈组在传输性能方面有了明显的提升。

