综合考虑早晚高峰交通流特性的可变车道布置方案
陈婷婷, 贾顺平
(北京交通大学交通运输学院, 城市交通复杂系统理论与技术教育部重点实验室, 北京 100044)
随着城市化的发展,城市的规模逐渐增加。受到城市规划的影响,居民的居住区多在城市外围区域,而工作区多在城市中心区,这直接导致了城市交通流的“潮汐现象”。所谓交通流“潮汐现象”,指的是早高峰进城方向(即居住区到工作区)交通量大,出城方向交通量小(即工作区到居住区);晚高峰时交通量情况则相反。交通流的“潮汐现象”造成了城市道路资源的浪费,重交通方向交通拥堵严重,而轻交通流方向交通通畅,道路资源未被完全利用[1-4]。
可变车道作为缓解城市早晚高峰时期交通流 “潮汐现象”的一种有效手段,被广泛应用于中国各大城市,如北京、上海、杭州等[3]。可变车道可以通过调整早晚高峰时期道路上部分车道的行车方向,实现对道路不同方向的车道数的重新配置,在不影响轻交通流方向车辆正常行驶的情况下,可变车道可以为重交通方向的车辆提供额外的通行能力,缓解重交通流方向的交通拥堵现象,减少城市道路资源的浪费[5-7]。
中外学者针对交通网络和交叉口出可变车道设计优化方法及其实施效果等方面进行了广泛而深入的研究。丁心茹[8]为解决城市中交通的潮汐现象,从道路系统的角度出发,通过建立双层规划模型来设计潮汐车道的配置方案;常玉林等[9]基于交叉口的实时交通状况构建了可变导向车道自适应控制模型,根据不同时段交叉口各进口道的需求,确定可变导向车道的具体配置和交叉口信号配时方案,并利用VISSIM仿真软件来验证所提出的模型;Wang等[10]提出了双层规划模型以重新配置疏散交通网络中的交通供给和交通需求,其中上层规划寻求最优的可变车道布置方案;Kotagi等[11]在城市中未划分车道的交通网络中设置可变车道,并利用微观仿真模型来评估可变车道的实施效果;为了评估设置左转可变车道对交叉口运行性能的影响,Wu等[12-13]设计了分析通行能力模型和延误模型,提出了感应式信号控制策略来提高实施左转可变车道的信号交叉口的运行能力;王艳丽等[14]通过视频交通图像获取车辆行驶数据来计算交通饱和度,根据道路双向饱和度的加权切换动态控制方式对潮汐车道进行自适应控制。
在可变车道布置方案优化中,既有研究大部分以交叉口或者交通网络为优化对象。在针对交叉口的研究中,学者主要集中在可变导向车道的控制方法和交叉口信号配时等方面,实施可变车道的交叉口的交通状况有所改善,但是缺乏对整个路网的实施效果的评估;在针对交通网络的研究中,学者主要通过优化模型来配置网络中可变车道的配置方案,但大部分的研究主要针对早、晚高峰中的单个高峰设计可变车道方案,很少考虑到城市交通流早、晚高峰的差异性,综合考虑不同时段可变车道的设置。
在既有研究的基础上,现从城市交通网络的角度出发,综合考虑了早、晚高峰时期交通流的差异性,建立了可变车道优化设置的双层规划模型,通过求解双层规划模型,同时优化设计出早、晚高峰时期网络中不同的可变车道布置方案,从而实现规划时期内交通网络总出行时间最小化的目标。此外,与既有研究不同,考虑了可变车道的投资费用对网络中可变车道布置方案的影响。对于所提出的双层规划模型,采用了嵌套Frank-Wolfe算法[15]的遗传算法[16]进行求解,最后通过算例分析可变车道对交通网络运行性能的影响。
1 可变车道设置问题分析
可变车道是指根据早、晚高峰时期城市交通网络的需求灵活地调整部分车道的行车方向的一种交通组织方式。如图1所示,该路段具有“潮汐交通”现象,双向交通流量不平衡,初始车道设置为每个方向三条车道[图1(a)],早、晚高峰时期,根据每个方向交通流的需求,变换每个方向上的车道数,如图1(b)、图1(c)所示,车道数被调整为单向4条车道和单向2条车道。可变车道的优化设计可以缓解高峰时期“潮汐交通”路段上交通拥堵的情况,降低城市交通网络中居民总的出行时间。
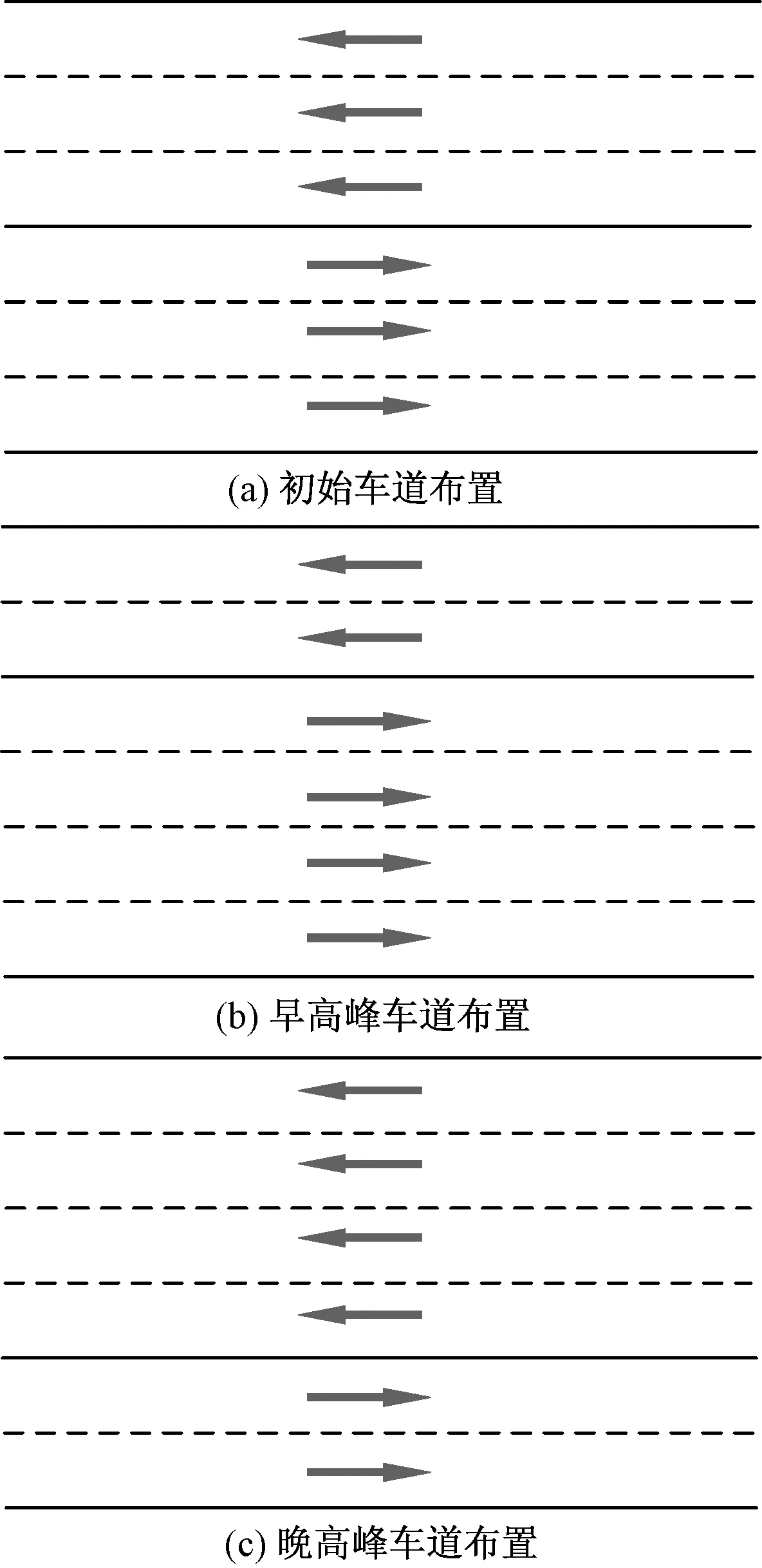
图1 可变车道示意图Fig.1 Deployment of reversible lanes
可变车道在改善城市交通拥堵的方面发挥了重要的作用,但是可变车道的设置需要综合考虑多方面因素。
(1)考虑设置可变车道的路段的交通流特征。当路段表现出明显的“潮汐交通”现象,即一个行车方向交通拥堵严重,车辆行驶缓慢,另一个行车方向车辆行驶通畅,道路资源未被完全利用,此时考虑设置可变车道。在保证轻交通流方向的基本通行能力的前提下,通过在重交通流方向增加可变车道及减少轻交通流方向的车道数,尽可能多的为重交通流方向车辆提供额外的通行能力。路段设置可变车道后,道路的通行能力应满足两个行车方向的交通需求,避免出现新的交通瓶颈[3]。
(2)从路网角度考虑可变车道设置的具体方案。对单个路段可变车道的调整可能会使该路段的交通拥堵情况有所改善,但是从整个路网的角度来看,孤立地调整每个出现“潮汐交通”现象的路段,可能会影响整个交通网络的高效运行。由于交通网络是连续的,一条路段上交通量的调整可能会影响网络中其他路段交通量的变化,导致可变车道的实施效果变差,影响整个交通网络总的出行时间。
(3)综合考虑早、晚高峰时期交通流特点进行可变车道的优化设置。分别对早、晚高峰中的单个高峰进行可变车道的布置,单一高峰时期网络的总出行时间可能有所降低,但是工作量大,且从系统的角度出发,早、晚高峰时期路网的总的出行时间的减少效果可能不明显。
综上所述,可变车道的设置应从路网的角度出发,系统地考虑可变车道的具体设置方案,解决城市交通网络早、晚高峰时期交通流不平衡的问题,减少居民的出行时间。
2 可变车道设置的双层规划模型
给定有向图N=(V,A)表示城市交通网络,其中V表示网络节点集,A表示有向路段集。对于网络中任意一有向路段a∈A,其反向路段记为a′∈A。高峰时期集合为M={1,2},其中m=1表示早高峰,m=2表示晚高峰。
集合定义:R表示网络中起讫点(origin destination, OD)对起点的集合,任意起点r∈R;S表示网络中OD对终点的集合,任意终点s∈S;Krs表示任意点对(r,s)的路径集合,点对(r,s)的任意路径k∈Krs。
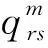
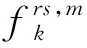
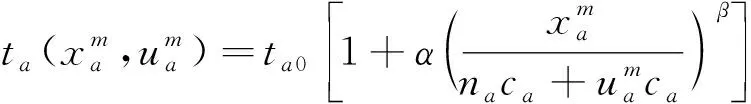
(1)
式(1)中:α、β为待定的参数,现取α=0.15,β=4。
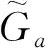
交通管理者根据网络中交通流的特性,调整网络中部分车道的行车方向,以此降低网络中出行者的总出行时间。道路上可变车道的设置,可能会影响网络中其他路段交通流的重新配置,从而影响网络中出行者的出行路径选择行为。出行者的路径选择又会影响到交通管理者对于可变车道设置方案的调整。这是一个典型的主从博弈模型,可采用双层规划模型对本文所研究的问题进行建模。
2.1 上层规划
上层规划模型是一个投资决策问题,交通管理者通过设计最优的可变车道布置方案,使路网中出行者的总出行时间最小化,模型表述为
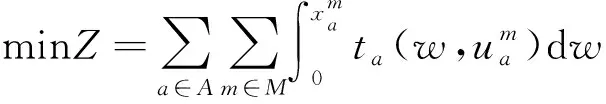
(2)

(3)
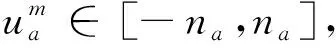
(4)

(5)
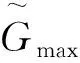
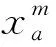
2.2 下层规划
在下层规划模型中,出行者根据上层规划模型确定的可变车道布置方案进行出行路径选择。假设出行者的路径决策遵从Wardrop用户平衡原则,即所有出行者都能选择最短路出行,以最小化出行者的出行时间。模型表述为
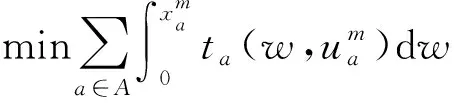
(6)
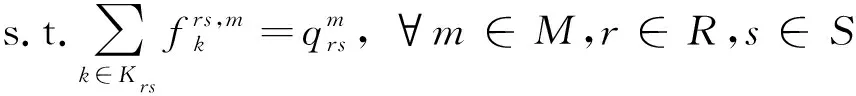
(7)

(8)

(9)
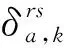
通过下层模型,可以分别对早、晚高峰时期的交通需求进行分配,求得任意路段上的交通流量,用以评价上层模型中可变车道设置方案的优劣。
3 求解算法
双层规划模型的上层模型寻求最优的路网的可变车道布置方案,结合下层用户平衡模型的交通流分配结果,从而得到最优的可变车道设置方案。该问题是一个混合整数规划问题,其中上层模型的决策变量为整数,下层模型的决策变量为实数,它是被公认的求解较为困难的优化问题之一。采用嵌套Frank-Wolfe算法的遗传算法对所研究的问题进行求解,遗传算法用于寻求可能的可变车道布置方案,Frank-Wolfe算法对每个可变车道布置方案进行交通流分配。基本步骤如下。
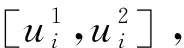
(2)种群初始化。
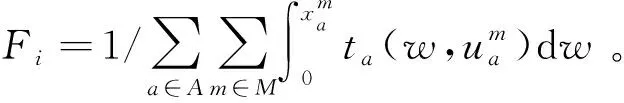
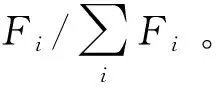
(5)交叉。给定交叉概率,当满足交叉概率时,对种群中的个体两两进行交换。具体的交换方式为:随机生成两个插入点,交换两个个体两个插入点所在行之间所有行的编码,从而得到新的子代。
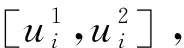
4 数值试验
为了验证所提出的双层规划模型及嵌套Frank-Wolfe算法的遗传算法的有效性,采用经典的Sioux Falls网络,对可变车道的实施效果进行分析。
4.1 算例构建
Sioux Falls网络[17]是一个中型网络,该网络有24个节点,76个有向路段,528个OD对。在网络原始通行能力的基础上,根据车道基本通行能力,生成每个路段上的车道数。为了反映“潮汐交通”现象,在网络区域划分的基础上(虚线所划定区域为工作区,外围区域为居住区),对工作区和居住区之间的OD需求进行调整。Sioux Falls网络中区域划分和路段车道数如图2所示。

图2 Sioux Falls网络区域划分与路段车道数Fig.2 Regional division and lane numbers in the Sioux Falls network
4.2 算例求解
4.2.1 不设置可变车道
在不设置可变车道的情况下,使用Frank-Wolfe算法对网络中的OD需求进行交通流量分配,此时可变车道的投资费用为0,网络中出行者的总出行时间为218 892(无量纲)。
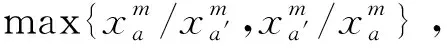
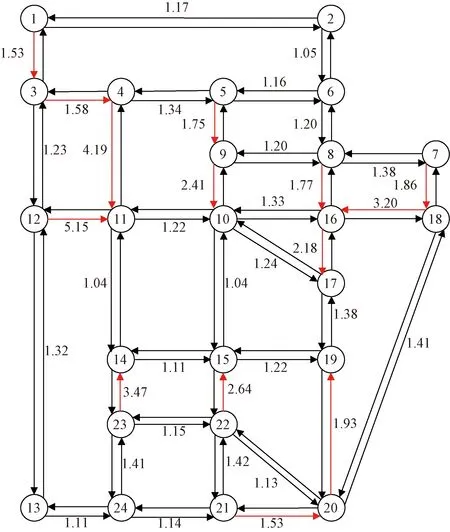
图3 早高峰未设置可变车道路段流量比Fig.3 The flow ratios during the morning peak
4.2.2 设置可变车道
当不考虑可变车道投资费用时,网络中最优的可变车道布置方案如表1和图4所示,此时,网络中出行者的总出行时间为171 117,与不设置可变车道相比,网络中出行者的总出行时间下降了21.8%。如表1所示,可变车道的设置在早、晚高峰呈对称布置,这主要是由于对早、晚高峰的交通需求进行了对称处理,所以出现对称的可变车道布置结果是较为合理的。当早、晚高峰需求不对称时,可变车道布置将可能出现不对称的情况。
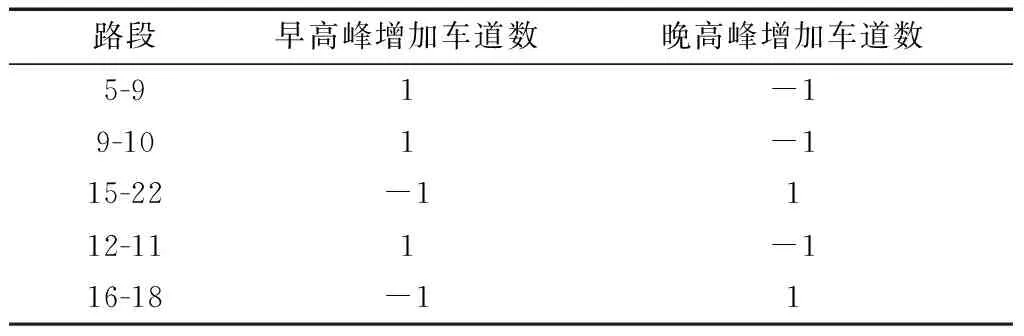
表1 可变车道优化方案
如图4所示,可变车道设置的位置主要位于网络中交通流不平衡现象较明显的路段,即连接工作区与居住区的路段,如路段5-9、路段9-10、路段8-16、路段12-11和路段15-22等。
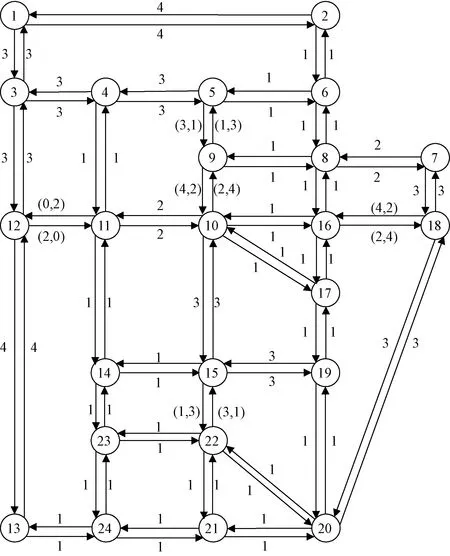
括号中的数字分别表示早、晚高峰时期路段5~9的车道数
在实施可变车道方案后,网络中出现了单行交通,路段12-11在早高峰时期为单行线,路段11-12在晚高峰时期为单行线。实施单向交通可能使习惯选择该路段的出行者的出行时间有所增加,但是从系统的角度来看,路段12-11和路段11-12在早、晚高峰时期分别实行单向交通将有利于降低整个网络的出行时间。
4.2.3 可变车道投资费用的灵敏度分析
为了分析投资费用限制对最优可变车道布置方案的影响,采用嵌套Frank-Wolfe算法的遗传算法进行了一系列数值实验。在满足最大投资费用的前提下,增加可变车道的投资费用可视为增加可变车道的数量。投资费用(即可变车道数量)与网络出行者的总出行时间关系如图5所示。

图5 投资费用的边际效用Fig.5 Variation tendency with respect to the marginal utility of the investment
如图5所示,反映了投资费用的(即可变车道数量)边际效用变化趋势。当可变车道数从0增加到4时,总出行时间减小幅度较大。当可变车道数从8增加到10时,总出行时间下降较为平缓。总体来看,在满足投资费用限制的前提下,当增加投资费用时,即增加可变车道数,网络中出行者的总出行时间逐渐减小,这说明可变车道在发挥缓解不平衡交通流、改善交通拥堵和提高网络运行性能方面发挥着重要的作用。此外,如图5所示,路段12-11和路段11-12存在于所有最优的可变车道布置方案中,即2、4、6、8、10条可变车道。结合图3路段流量比,可知路段12-11和路段11-12位于连接居住区和工作区的主要道路上,交通流不平衡现象较为严重,在路段12-11和路段11-12上设置可变车道将有利于改善交通系统的运行状况。
5 结论
从交通网络的角度出发,研究了综合考虑早、晚高峰交通流特性的可变车道布置方案。针对所提出的问题,构建了可变车道布置的双层规划模型,并设计了一个嵌套Frank-Wolfe算法的遗传算法。上层模型主要决策最优的可变车道布置方案,下层模型根据上层决策对早、晚高峰的交通需求进行分配,得到的交通分配结果反馈上层模型以评估可变车道布置方案的优劣。基于Sioux Falls网络对所提出的模型及算法进行验证,得到如下结论。
(1)在网络中设置可变车道后,可以缓解网络中路段交通流不平衡现象,大大减少网络中出行者的总出行时间。与不设置可变车道相比,在引入可变车道后,网络中出行者的总出行时间下降了21.8%。
(2)设置可变车道后,可能会存在部分路段被更改为单向交通的情况。单向交通可能会导致习惯选择这些路段的出行者的出行时间增加,但是从系统的角度来看,部分的单向交通对于缓解整个网络的出行时间是有益的。
(3)在投资费用允许的情况下,尽可能多地增加网络中可变车道的数量,对于提高整个网络的运行性能、减少网络总出行时间有积极的作用。

