销铰连接M36高强螺栓常幅疲劳性能试验

焦晋峰， 李 渊 ， 刘 勇， 郝海舒， 邢 颖

(1.太原理工大学土木工程学院， 太原 030024； 2.山东电力工程咨询院有限公司， 济南 250013)

销铰连接因其构造简单、传力明确、施工方便、经济环保等优点，被广泛应用于各类工业和民用建筑中。参看文献[1]，在大跨度钢结构体系建筑中，其受拉或受压杆件铰接节点经常采用销铰连接。而在风荷载、地震荷载等循环荷载作用下，大跨度钢结构的销铰节点可能发生疲劳失效，进而导致结构发生局部坍塌甚至整体破坏，造成不可估量的损失。《钢结构设计标准》(GB 50017—2017)[2]首次在钢结构领域引入销轴连接的相关条文，但与国家现行的其他行业规范一样，都仅仅只考虑销铰连接的构造要求及静力承载性能，其疲劳验算方面尚存空白。

中外学者针对销铰连接开展了一系列理论与试验研究：王帅等[3]利用数值模拟对销轴进行参数分析，得到其应力集中位置，推导了合理的销轴承载力计算公式；颜东煌等[4]以佛山东平大桥为背景，结合试验与数值模拟结果对销铰节点接触应力进行分析，研究了不同参数对其大小及分布的影响；丁大益等[5-6]以山东邹城国际会展中心桁架销铰节点为研究对象，设计4个不同尺寸缩尺模型的静力载荷试验，结合有限元分析结果，研究销铰节点的承载能力以及节点和楼面桁架的组合受力性能；潘汉明等[7]针对广州电视塔双向铰节点进行了两个典型节点的足尺试验和有限元分析，研究了节点的极限承载力和破坏模式，分析了影响节点受力性能的因素；许强等[8]讨论了销轴抗弯计算公式的选用及销孔间隙对承载力的影响，并探讨了销轴的接触应力问题；张彩亮等[9]对比了中、美、欧钢结构规范中销轴连接的计算公式，分析了其中的计算差异；Iyer[10]通过数值模拟研究了材料属性、摩擦系数、耳板尺寸等因素对销铰节点接触应力分布的影响；Duerr等[11]总结了早期对销铰连接受力特性的大量研究和试验数据，建立了一组销轴弹性应力分布、形变及极限强度的公式，来定义销轴的强度及受力性能,同时提出上耳板销孔压力的有效分布宽度概念；Pedersen[12]通过包括接触模拟在内的有限元分析，研究销铰节点的应力集中影响因素，并通过优化设计来降低销铰连接的应力集中系数；Kavoura等[13]评估了现有公式对柱底板销铰连接的适用性，并将试验所得节点的转动刚度和抗弯承载力与美、欧设计规范计算所得的值进行了对比，得出欧洲规范计算所得的转动刚度精确度不高。

综上所述，目前中外针对销铰节点的研究较少，且集中于研究销铰节点在静力荷载下的受力分析，针对其疲劳性能的研究较少。为探讨销铰节点的疲劳性能，现利用9组销铰连接高强螺栓常幅疲劳试验结合ABAQUS有限元分析软件，研究销铰节点常幅疲劳性能及应力分布规律，揭示其疲劳破坏机理，建立合理的疲劳验算公式。

1 销铰连接高强螺栓疲劳试验

1.1 试件力学性能指标

基于试验目的与试验条件，选取规格为12.9级的M36高强双头螺栓作为试验对象，试件材质为35CrMoA，其尺寸公差及化学成分均满足国家现行的各项规范与标准。参考《紧固件机械性能螺栓、螺钉和螺柱》(GB/T 3098.1—2010)[14]，选取了3个试件用于静力材性试验，得到了试件的弹性模量，其余各项力学性能指标参考产品说明书，具体数值如表1所示。

表1 螺栓试件力学性能参数

1.2 试件设备

疲劳试验主要设备为Amsler1200脉冲疲劳试验机和DASP动态应变采集仪。Amsler试验机采用力控制加载，允许最大荷载值为1 000 kN，最大频率800 r/min。此外，在试验过程中，螺栓中段螺杆处轴向布置2个单向应变片，间隔180°，以监测螺栓在整个试验过程中的应力应变变化。

1.3 加载装置

试验结合试验目的与条件设计了一套加载装置，该装置能够满足销铰连接高强螺栓疲劳试验。销铰连接高强螺栓节点区别于典型销轴节点的双端耳板单中耳板设计，具有双端耳板双中耳板，而试件的实际受力与典型销轴连接基本一致。加载装置如图1、图2所示。考虑实际情况，试验同时进行两个节点的疲劳试验，如图3所示，上、下两节点通过十字板+圆钢管-焊接空心球节点(“板+管-球”节点)连接，在尽量保证两节点相对独立受荷的情况下，极大程度地节约了试验时间，提高了效率。

图1 加载装置模型示意图Fig.1 Model of loading device

图2 加载装置示意图Fig.2 Loading device

图3 双节点装置加载Fig.3 Loading device of double joints

1.4 疲劳加载制度

通过切向拉伸试验获取试件疲劳破坏时的一系列数据点，拟建立反映销铰连接高强螺栓常幅疲劳性能的S-N曲线，因此参考StandardPracticeforConductingForceControlledConstantAmplitudeAxialFatigueTestsofMetallicMaterials(ASTM E466—15)[15]、《金属材料轴向等幅低循环疲劳试验方法》(GB/T 15248—2008)[16]、《金属材料疲劳试验轴向力控制方法》(GB/T 3075—2008)[17]等国家现行标准的规定，制订了符合工程实际同时满足试验要求的疲劳加载制度，具体如下。

1.4.1 应力比

结合实际工程设计、应力比控制及安全因素考虑，选定试件1、1′应力比为0.2，其余各试件应力比为0.1进行试验。

1.4.2 预拉力

试验螺母仅起约束作用，限制螺栓杆件的轴向位移，确保试件在试验过程中只受到加载装置传递的荷载，预紧力约等于零。

1.4.3 交变荷载和加载频率

试验参考文献[15]在力控制下施加具有恒定振幅正弦波信号的周期性载荷。同时考虑工程实际和试验仪器限值等因素，确定加载频率为 200 r/min。

1.4.4 加载制度

根据大量疲劳试验得出，应力水平直接影响构件破坏的疲劳循环次数。疲劳试验的应力水平包括最大应力(σmax)和最小应力(σmin)两个指标，最大应力结合试验设备、试验目的及材料力学性能指标确定，最小应力由给定应力比计算得出。在确定应力比的情况下，以4个等级不同的应力幅为参考变量对9个试件进行加载。本次疲劳试验的常幅加载制度如表2所示。

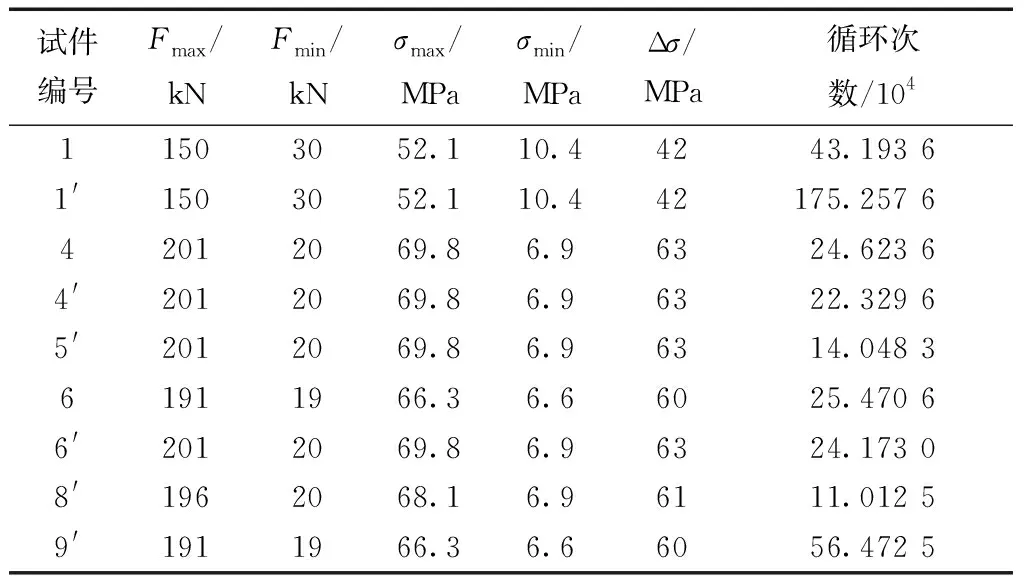
表2 销铰连接M36高强螺栓常幅疲劳试验结果

1.5 疲劳试验现象及结果

1.5.1 疲劳试验结果

疲劳试验皆以试件完全断裂作为高强螺栓的疲劳失效判据。试件发生疲劳断裂时，试验加载仪器同步停止。记录全部9个试件发生疲劳失效时对应的应力水平及疲劳破坏循环次数，如表2所示。根据所得试验结果，以疲劳试验加载应力幅为纵坐标，循环次数为横坐标，得到试件应力幅(Δσ)与循环次数(N)的对应关系如图4所示。由图4可知，数据虽较为离散，但整体可见试件的疲劳循环次数与加载应力幅成反比，即加载的应力幅越大，试件发生疲劳破坏的循环次数越低。

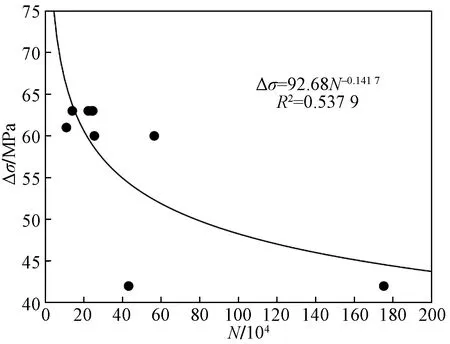
图4 Δσ-N曲线Fig.4 Δσ-N curve

1.5.2 疲劳断口分析

9个试件的断口均表现出良好的疲劳破坏特征，其中选取两个较为典型的疲劳试件断口1和1′做宏观与微观分析。

图5为试件1的疲劳断口照片。由图5(a)宏观断口可知：该试件疲劳断口分为界线较清晰的3个区域：疲劳源区，疲劳扩展区(分为稳定扩展区和快速扩展区)，瞬断区。裂纹起始于断口右端的疲劳源，整体沿径向向左发展；疲劳扩展区约占断口面积的35%，表面光滑平整，为疲劳裂纹之间不断相互挤压、摩擦所致；瞬断区约占断口面积的60%，表面粗糙纹路杂乱，为试件有效断面不断减小，发生瞬时断裂所致，在断口左侧形成剪切唇。图5(b)、图5(c)为疲劳源区50倍与200倍微观图，可见收敛性点疲劳源区，裂纹沿径向与环向间多方向发展；图5(d)、图5(e)为稳定扩展区500倍与2 000倍微观图，可见该区域表面较平整，疲劳辉纹密布；图5(f)、图5(g)为快速扩展区500倍与2 000倍微观图，可见该区域表面较粗糙，局部出现韧窝；图5(h)为疲劳瞬断区500倍微观图，可见该区域表面粗糙，起伏明显，出现大量韧窝，其中一些韧窝因颗粒脱落而形成空洞。

①为疲劳源区；②为疲劳扩展区(分为稳定扩展区和快速扩展区)；③为瞬断区

图6为试件1′的疲劳断口照片。由图6(a)宏观断口可知：疲劳源区位于断口左上；疲劳扩展区约占断口面积的70%，其中稳定扩展区约占40%，表面平整光滑，颜色暗淡，快速扩展区约占30%，表面较粗糙，颜色光亮，稳定扩展区与快速扩展区界线较清晰；瞬断区约占断口面积的25%，在断口右下形成小凹槽；对比试件1与1′各区域所占面积，可知试件1′经历了更长时间的裂纹扩展阶段，而其疲劳循环次数恰验证了此观点。图6(b)、图6(c)为疲劳源区50倍与200倍微观图，可见明显线疲劳源区，裂纹起始区域可见成排垂直于主应力方向的细小波纹；图6(d)、图6(e)分别为稳定扩展区500倍、2 000倍微观图，可见大量疲劳辉纹，局部区域复数裂纹沿单一方向不断扩展；图6(f)为快速扩展区500倍微观图，可见该区域渐有起伏，裂纹扩展方向多样；图6(g)、6(h)为疲劳瞬断区500倍、1 000倍微观图，可见该区域颜色较亮，有金属光泽，起伏明显，存在大量韧窝。

①为疲劳源区；②为疲劳扩展区(分为稳定扩展区和快速扩展区)；③为瞬断区

1.5.3 试件断裂位置

为研究销铰连接高强螺栓轴向的应力分布规律，本次试验统计各试件疲劳断裂发生的位置，具体记录内容为断裂发生的区域及断裂位置沿轴向距端点的距离。考虑到加载装置及试件的对称性特点，如图7所示，基于1/2螺栓试件的剖面绘制坐标轴来进行统计，统计结果如表3所示。

表3 螺栓疲劳断裂位置

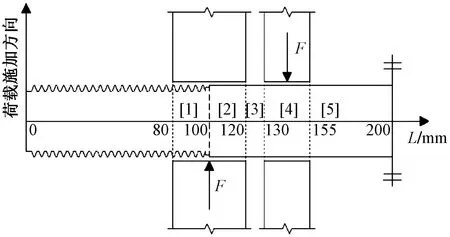
图7 1/2试件剖面简图Fig.7 Sectional view of half specimens

2 数值模拟

销铰连接工作状态下受到剪力与弯矩的复合作用，为研究销铰连接高强螺栓的实际受力情况，进行数值模拟得到试件受切向拉伸荷载时的理论应力集中系数及应力分布规律。

2.1 有限元模型建立

使用有限元分析软件ABAQUS对加载装置及M36高强螺栓试件建立合理简化后的等比例模型：考虑到整个加载装置及试件受力的对称性特点，取1/2结构进行分析，加载装置对称面一端采用固端约束；原加载装置由上加载头顶板的四个螺栓连接疲劳试验机传递荷载，将其简化为上加载头顶面的等效均布面荷载；简化M36高强螺栓试件两头固定的螺母，替换为试件两端的轴向位移约束；高强螺栓试件的材料属性参考材性试验所得力学性能指标，加载装置材料属性参考标准40Cr的性能参数。单元类型采用C3D20，该单元类型特点为能精确模拟出模型的应力结果。网格划分后的模型如图8所示。

图8 模型网格划分效果Fig.8 Result of model meshing

2.2 模拟结果

在整个疲劳试验过程中，M36高强螺栓试件始终处于弹性阶段，所以在线弹性范围内进行数值模拟。拟对模型施加9 MPa的均布面荷载，此时高强螺栓所受名义应力σn为420 MPa，模拟结果如图9所示。

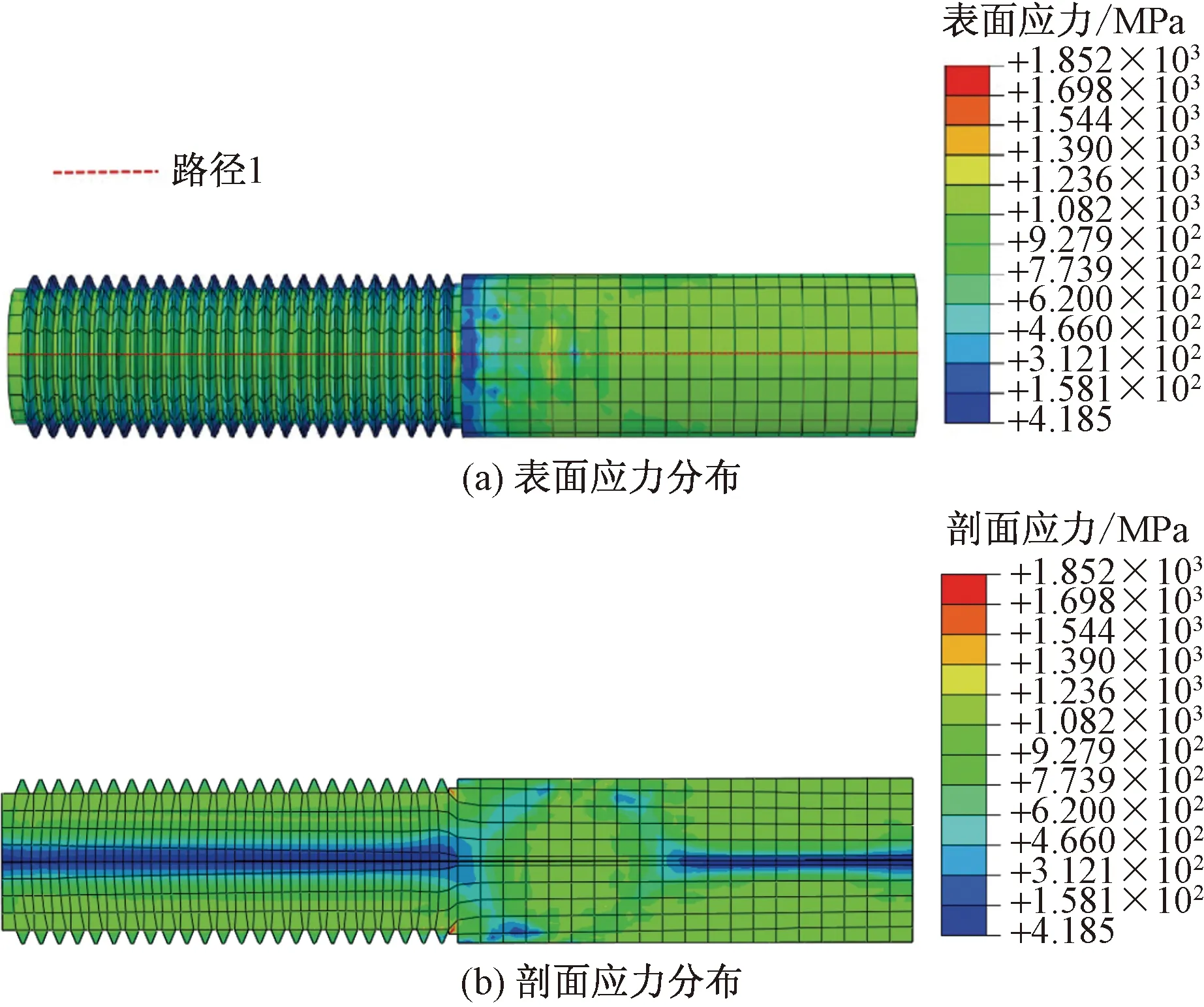
图9 1/2螺栓模型表面应力和剖面应力分布Fig.9 Surface stress and section stress distribution of half bolt model

2.3 试验与模拟结果对比

为准确得出试件轴向的应力分布规律，垂直于主应力方向在试件表面确定路径1，如图9(a)所示。对模型进行后处理得到路径上各结点的局部应力(σc)，路径1上各结点局部应力与名义应力的比值曲线如图10所示。模拟结果比对1.5.3节试件疲劳断裂位置可知：峰值应力出现在高强螺栓承压面的第一节螺纹齿根处，此处应力集中严重，理论应力集中系数Kt=4.409，试件4、6′、8′断裂位置位于此处临近区域；外耳板与内耳板对螺栓的挤压处应力水平较大，局部应力与名义应力比值为2.592～3.176，试件1、1′、9′断裂位置位于此处临近区域；试件4′、5′、6断裂位置位于内耳板孔隙对螺栓杆件的挤压处，此处局部应力与名义应力比值为2.593～2.741。数值模拟结果中试件的应力突变位置与疲劳试验中试件的破坏位置基本吻合。

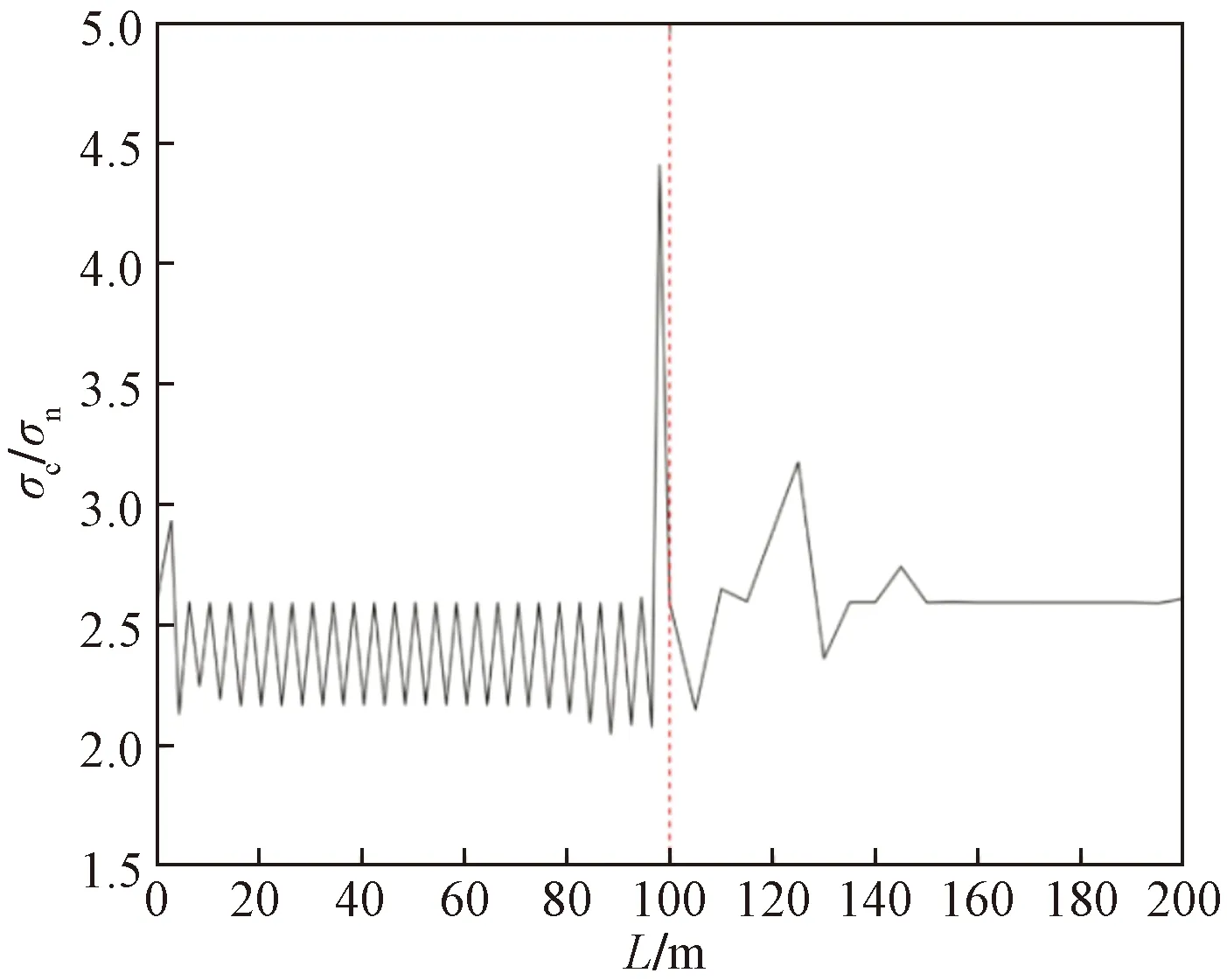
图10 路径1各结点局部应力与名义应力比Fig.10 The ratio of local stress to nominal stress at each node of path 1

3 S-N曲线及疲劳计算公式建立

对上述所得9个销铰连接高强螺栓常幅疲劳试验结果进行最小二乘拟合。当采用保证率为95%时，对应的计算公式为

lg(Δσ)=algN+b-1.645s

(1)

式(1)中：Δσ为应力幅；N为试件的疲劳寿命；a、b由试验数据拟合确定，与材料属性、加载形式等有关；s为样本标准差。

拟合后的S-N曲线如图11所示，对应销铰连接高强螺栓的疲劳回归方程为

lg(Δσ)=-0.154 9lgN+2.603 3±0.133 2

(2)

由图11可知，lg(Δσ)与lgN呈现出良好的线性相关关系。由式(2)计算可得，销铰连接高强螺栓疲劳循环次数为2×106次对应的名义允许应力幅[Δσ]2×106=42.39 MPa。

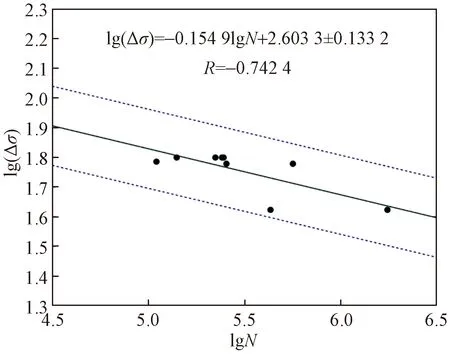
图11 试验lg(Δσ)-lgN曲线Fig.11 Experimental lg(Δσ)-lgN curve

建立螺栓的缺口允许应力幅表达式为

[Δσ]f=[Δσ]2×106Kt

(3)

由式(3)可得，销铰节点高强螺栓对应的缺口允许应力幅[Δσ]f=186.90 MPa。

《钢结构设计标准》(GB 50017—2017)中16.1.3条：疲劳计算应采用基于名义应力的容许应力幅法，名义应力应按弹性状态计算，容许应力幅应按构件和连接类别、应力循环次数以及计算部位的板件厚度确定。销铰连接构件受弯剪作用，在《钢结构设计标准》(GB 50017—2017)中尚无对应连接类别参数，与标准中连接类别为Z11和J2即普通螺栓受轴向拉伸作用与螺栓受纯剪切作用下的容许名义应力幅进行对比。

正应力幅的疲劳计算公式为

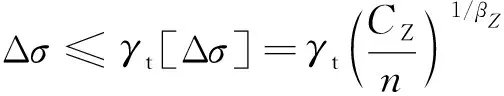
(4)

式(4)中：Δσ为常幅疲劳的容许正应力幅，对于非焊接部位：Δσ=σmax-0.7σmin；连接类别按Z11考虑时，将相关系数CZ=0.25×1012、βZ=3、γt=1.0代入式(4)可得

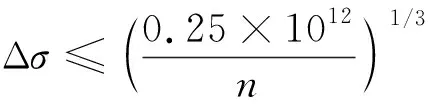
(5)

由式(5)可得，连接类别Z11螺栓对应2×106次允许名义正应力幅[Δσ]Z11=50 MPa。

剪应力幅的疲劳计算公式为

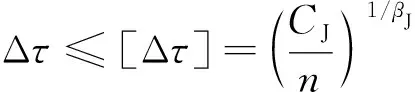
(6)

式(6)中：Δτ为常幅疲劳的容许剪应力幅，对于非焊接部位：Δτ=τmax-τmin；连接类别按J2考虑时，将相关系数CJ=2×1016、βJ=5代入式(6)，可得疲劳计算公式为

(7)

由式(7)可得，连接类别J2螺栓对应2×106次允许名义剪应力幅[Δτ]J2=100 MPa。标准与试验对比结果如图12所示，试验得销铰连接高强螺栓循环次数为2×106次，对应的允许名义应力幅和缺口允许应力幅分别为标准中连接类别Z11螺栓对应名义容许正应力幅的84.78%、373.8%，为连接类别J2螺栓对应名义允许剪应力幅的42.39%、186.9%。

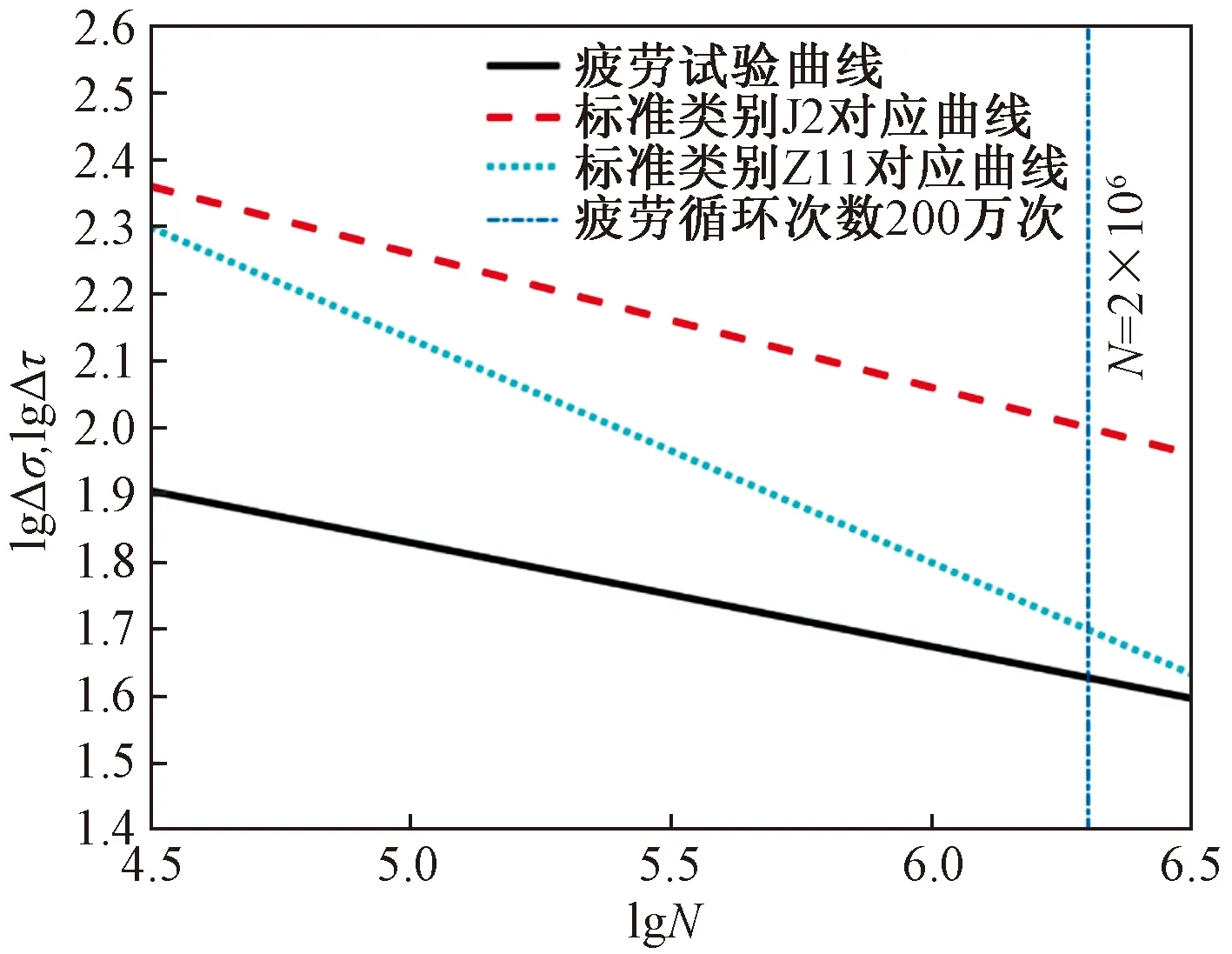
图12 试验与标准S-N曲线对比Fig.12 Comparison of S-N curve between test and standard

4 结论

通过试验研究9个销铰连接M36高强螺栓常幅加载的疲劳性能，得到以下结论：

(1)通过数值模拟获得销铰连接高强螺栓沿轴向的应力分布，其承压面下第一节螺纹齿根处应力集中严重，理论应力集中系数Kt=4.409；此外内外耳板间对杆件挤压位置局部应力水平较大，最大值为名义应力3.176倍。模拟结果中应力突变位置与疲劳试验试件破坏位置基本吻合。

(2)9个试件断口均呈现良好的疲劳破坏特征。对典型断口1、1′进行宏观与微观分析，分析可得：其疲劳源皆位于试件表面，裂纹从多点收敛性疲劳源或线疲劳源起始，沿环向与径向间多个方向同时扩展，使试件有效断面不断减小，最终发生瞬时断裂。

(3)根据疲劳试验拟合得到95%保证率下疲劳S-N曲线，计算得销铰连接高强螺栓疲劳循环次数为2×106次对应的名义允许应力幅[Δσ]2×106为42.39 MPa，分别为《钢结构设计标准》(GB 50017—2017)中类别Z11螺栓与类别J2螺栓对应允许应力幅的84.78%和42.39%；得到销铰连接高强螺栓缺口允许应力幅[Δσ]f为186.9 MPa，分别为标准中类别Z11螺栓与类别J2螺栓对应允许应力幅的373.8%和186.9%。