优化问题链设计，上好几何开门课

姚程琳

一、问题链设计在本课中的运用

本节课是圆的开篇第一节课，在此之前，学生对圆的了解有半径、直径的概念。本节课的重点是通过操作、实验的方式来体会和感受圆的周长公式。学生在这堂课要体会圆的公式的由来，要理解仔的含义，要建立起用操作实验的方法来验证数学知识的思维方式。为此，本堂课在教学中应包含以下三个必经重要环节：

1.创设情境，导入提出问题：从数学的应用性和生活化的角度出发，提出问题。确保这个问题是客观存在的真问题，且学习者具有要研究的知识储备和基本方法，清楚解决问题中的关键障碍。

2.合作交流，探寻解决方案：这是课堂的核心步骤，学生可小组讨论，经历分工、制定探究方案、实验验证、反思，再尝试合作探究过程，逐步分阶段解决问题。在此过程中，教师应在想法冲突处、思维关节点兼顾学生认知水平，给予引导和点拨，做有效提问。

3.变形应用，反思与评价：鼓励学生及时反馈想法，进行多元客观的评价，从而归纳问题，得到数学素养的提高与发展。

二、问题设计的具体思路

为了给学生充分的思考空间，教师应担当引路不指路的角色，我在设计问题时基于课程要求，促进学生对话，关注课堂理解。设计的主要问题如下：

1.创设情境，导入提出问题

（1）复习圆及圆的相关概念；

（2）情景引入。

国王想与阿凡提比赛，规定皇家小花驴沿直径为100 m的圆形路线跑，阿凡提的小黑驴沿着边长是100 m的正方形路线跑。看谁先回到出发地，如果他们同时出发，这样的比赛公平吗？为什么？

【问1】要比较比赛是否公平，我们应该比较什么呢？

2.合作交流，探寻解决方案

（1）剖析和分析问题。

【问2】回忆我们学习过的图形的周长，你能说出哪些图形的周长计算方法？

生：正方形、长方形、三角形、平行四边形的周長公式。

师：看来在计算周长之前，我们需要知道圆的周长公式。然后才能运用公式进行计算。所以我们今天要解决的问题可以分为两部分。

第一部分：圆的周长公式是什么？

第二部分：如何运用公式？

（2）逐步探究、获取新知。

【问3】观察生活中的圆，你认为是什么决定了圆的周长？

生：半径或者直径。

师：我们通过观察，发现圆的周长与直径有关。所以我们大胆地猜测，要计算圆的周长，先要知道它的直径或半径。

【问4】古人有“周三径一”的说法，你认为可信吗？

学生活动：用测量的方法，验证“周三径一”的说法。

第一步：测量直径。常见方法有两种：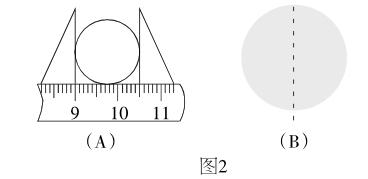

第二步：测量圆的周长。

常见方法有两种：（1）绕绳法；（2）滚动法。

第三步：记录数据：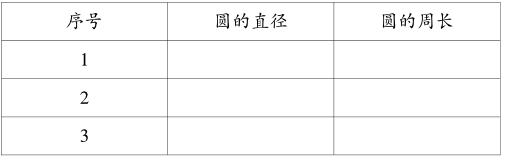

学生结论：古人“周三径一”的说法存在误差，通过实验及计算可以看到，这个数并不是3倍。

（3）几何直观地解释了圆的周长与直径比值的取值范围。

【问5】除了实验操作，还有什么方法能够解释圆的周长并不是半径的3倍？

（4）介绍仔的意义。

通过历代中外数学家对仔的精确度的研究故事，串联成一幅“仔的精确度”的发展图。让同学们感受人类在追求知识和真理过程中付出的不断努力，同时加深对仔是一个无线不循环小数的理解。

得出结论：圆的周长与圆的直径成倍数关系，这个倍数是一个固定的值，称为圆周率仔。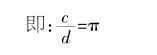

3.简单运用，评价反馈

【问6】有了圆的周长计算公式，你能编写一些与之相关的练习题吗？

4.评价与小结

【问7】

（1）今天我们解决了什么问题？

（2）你们小组在解决问题时，失败过吗？你获得了怎样的启示？

（3）你有什么要对小组的同伴说吗？

三、我的思考：如何上好几何开门课

1.测量误差影响结果，该如何处理

测量误差是操作过程中产生的不可避免的新问题，首先要认识到这是一个问题，然后要想办法解决它。在我播放完视频后，就有同学举手，说自己的计算结果是2.96，不在3到4的范围内。

此时，我意识到，这不是一次应忽略的插曲，而是使用操作实验方式研究问题的过程中必然会遇到的问题，学会正视和解决误差是学生应具备的科学探究素养。所以，我立刻追问：“大家觉得为什么会出现这样的情况？”同组的同学说：“应该是我们的测量有很大误差。”我再追问：“怎么办呢？说不定你们没有误差，是一个巨大发现。”

同学表示要排除这个问题最好的方法就是多测量几次。结果发现圆的周长足足少了2厘米，虚惊一场。

2.为什么要大费周章地体验无法得到精确值的实验

在设计课堂环节时，我曾犹豫过验证试验是不是本节课的一项重点。这个试验的目的是什么？起初，我的理解是让学生理解周长是直径的倍数，但是我发现由于测量误差，数据是波动的，学生并不能很好地体会这点。之后，我从问题解决的角度看待这个“注定失败”的实验，我认为这是让学生重走前任研究的路，通过亲历研究过程，感受到测量的误差对实验结果的影响，明白了仔是古人坚持严谨反复验证的巨大突破，感悟解决问题需要的执着和严谨的治学态度。

3.优化问题链，促进课堂对话

通过一节课层层深入的问题引导，在最后的小结评价环节，学生的发言令我欣喜，在课堂的小组讨论中，本以为见证了一切的我，听到了孩子们看到的课堂另一面。有同学劝告小组应该准备一个大一些的圆，而不是瓶盖，这样数据的误差对实验结果影响会更小；有同学表示，这个圆周长的学习让他明白了为什么先学习正方形、四边形，这样“有角”的图形后才能学习圆的的周长。

学生的收获中，满满的体现了他们思维的发展、能力的生长，对于系统解决一个问题的意识逐步形成。同时，也让我理解过往的教学，无异于有些思维降级，重点投喂不利于高阶思维的培养，只有让学生经历这样完整的、有插曲有失败的过程，才能激发学生的自我学习力和生长力。