论估算教学的严谨性与学生可接受性

周畅

《估算》教学一直是一个困扰老师们的难题，笔者结合人教版二年级上、下册涉及的估算问题，和三年级上册的《估算》解决问题，根据数学知识的严谨性和学生可接受性，提出有效解决估算中估大估小的问题。

教材最开始出现《估算》是在二年级上册《100以内的加减法》的一道练习题第（2）问：已知玩具飞机、小汽车、火箭、轮船单价分别为23元、14元、27元、30元，问50元可以买哪几件玩具？这道开放题，贴合孩子们的实际生活，非常有现实意义。笔者认为除了精确计算，还可以渗透估算意识，培养孩子们的数感，如二十几加十几肯定能买，二十几加二十几可能能买，对孩子们后续的估算教学会很有帮助。

一、结合学生可接受性，选择适当的估算精确度

孩子们正式学习估算是在二年级下册《萬以内的加减法》中关于估算解决问题的例题。电话机单价：358元，吹风机单价：218元，500元买这两件商品够吗？孩子们都知道把358和218加起来求和，看是否超过500，可是358+218这种三位数加三位数的加法还没学。教材出示的解题思路：电话机超过了300元，电吹风超过了200元。300+200=500，得出结论：带500元肯定不够。因为教材没有出示具体的解题算式步骤，老师们各出奇招。有这样的：358（360）+218（220）抑580（元）跃500（元）。笔者认为这拔高了对学生的要求，二年级下册的学生还只初步接触整百、整千数加减法，360+220这样的整十整百加减法的口算对他们还有一定难度。我们的估算有几种方法：可以把一个数估成整十数，即精确到十位；也可以把一个数估成整百数，即精确到百位；还可以把一个数估成整千数，即精确到千位……显然越往高位估，精确度越低，但越往高位估出的数，越容易口算。我们的数学课堂要考虑孩子们的可接受性。

二年级初步接触估算，估到整百整千即可解决问题。三年级的估算，安排在整十整百的加减法后面，给了我一个启发：是否估成整十整百就能解决问题？如例题：一到三年级来了221人，四到六年级来了239人，巨幕影院有441个座位，六个年级的学生同时看巨幕电影坐得下吗？出于孩子们的可接受性考虑，笔者在新授课时对教材例题做了一点微调：一到三年级来了212人，四到六年级来了234人，巨幕影院有440个座位，六个年级的学生同时看巨幕电影坐得下吗？孩子们基于二年级的估算基础，产生了不同的算法。

两种不同的估算方法，得到截然相反的答案，孩子们马上意识到算法1估成整百的方法，在三年级这道题里已经不适用了，他们自然而然地就会想到要往更精确的整十估了。

二、结合数学知识的严谨性，巧用数形结合，解决估大估小的问题

调整后的例题似乎仅仅处理了二年级和三年级估算的衔接问题。可三年级的估算解决问题，并非简单的估成整十整百就可以。如例题后面的做一做，原题如下：如果两个旅行团分别有196名和226名团员，巨幕影院有440个座位，这两个旅行团同时看巨幕电影坐得下吗？学生给出了两种算法：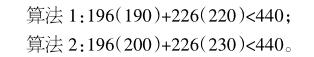

算法1的思路明显受例题的影响，以为估算都要往小估，但把196估成190，226估成220，都估小了，得到的和是410，这仅能说明196+226的和比410大，并不能确定就一定比440小。为了辅助孩子们能够更好地理解“为什么一个数比410大，无法保证就一定比440小”的问题，笔者还特意让孩子们动手画了数轴。

从图1中能够很明显地看出：比410大的数，可能比440小，也可能比440大，算法1无法得出确定结果。

算法2的学生认为：因为员怨远更接近圆园园，所以把员怨远估成圆园园；因为226更接近230，所以把226估成230……显然他虽然过程正确，但是他却是误打误撞对的。三年级老师们研讨时，有老师觉得估大估小容易把学生绕晕，也直接选择用这种四舍五入的方法。从四舍五入下手，虽然结果对，但道理不通，笔者认为这种方法是错误的。

正确的思路：把226估成230，把196估成200，都估大了，得到的估算值是430，精确值肯定要比430小，更加要比440小。

因为图是最直观、最容易理解的，大部分孩子都能够画出来，并且能很好地理解。感受到画图的好处，孩子们在做课后练习时，也就会不由自主地尝试画图的方法了。如果还有孩子图画不出来，笔者尝试了一种最笨的方法。依然用“196+226的和与440比大小”作例，因为孩子们刚学完整十整百的加减法口算，那么我们就看这三位数的十位和百位：190+220=410，因为个位还有数，那196+220的和肯定会比410大，但是无法和440作比较，再尝试往大估的方法。这种方法虽笨，但还是比较适合中下层的学生。

教有法而无定法，以上是笔者对于人教版三年级上册《估算》教学过程中的一点经验和体会，希望能够引起大家的一些思考。