基于单点脉冲宽度法的转子轴向位移径向测量∗
袁倩倩,朱永生,闫 柯,曹鹏辉,陈凯达,顾金芳
(1.西安交通大学现代设计与转子轴承系统教育部重点实验室 西安,710049)(2.上海天安轴承有限公司 上海,200125)
引言
转子系统作为旋转机械的核心支撑结构,其轴向位移在线监测技术是评估重大装备服役状态、预警故障的重要基础技术之一[1]。例如航空发动机、汽轮机等重大装备领域,大型转子系统的轴向窜动、轴向胀差等会引发转/静件轴向接触与摩擦,是影响转子运行性能、诱发故障的主要因素[2]。高精机床等智能制造领域,电磁轴承-转子系统中磁力轴承需要准确的轴向位移反馈控制转子运动,否则会导致转子不稳定,严重时会出现电磁轴承-转子系统故障[3-5]。在智能滚动轴承转子系统的在线服役调控技术中,转子轴承系统的轴向位移用于反映轴承内部载荷及预紧状态,并用于转子系统刚度调控、寿命评估和状态控制[6]。为了及时准确地发现转子系统运行状态,对转子轴承位移进行在线测量变得十分重要。然而,随着机械产品技术的不断发展,转子系统集成度不断提高,轴向位移传感器的安装位置和安装空间受到严重限制。
近年来,转子轴向位移的径向测量方法成为国内外学者的研究热点,但均需要对转子结构进行较大的改动。文献[7-8]通过在待测转子上加工台阶面,利用电涡流效应,提出了利用径向布置电涡流传感器测量磁悬浮轴承轴向位移的方法,分析了电涡流传感器与台阶安装间隙、台阶高度等对测量结果的影响。王晓光等[9]通过在待测转子回转表面加工锥面,当存在轴向位移时,利用锥面与传感器径向距离变化实现对轴向位移的径向测量。上述方法除了对转子结构有较大改动外,对多个传感器的灵敏度一致性、传感器相对位置与精度、传感器抗电磁干扰等提出了较高的要求,因此工程应用受到一定限制。文献等[10-12]在转子上增加磁性编码盘,然后利用两路霍尔传感器检测磁性编码盘,通过两路传感器输出信号的时间延迟计算得到转子轴向位移。该方法要求在转子设计中预留编码盘装配位置,因此在一定程度上影响了转子结构,同时编码盘安装困难,两路传感器需要更大的安装空间及安装平行度调试时间。
在转子轴向位移的径向测量中,为了尽可能不影响转子结构及安装空间,时振刚等[13]利用电感原理,在转子和定子径向布置电感线圈,通过转子轴向位移变化引起的线圈电感变化计算得到转子轴向位移。Zong等[14]利用电磁互感原理,研制了一种新型线性差动位移测量传感器,通过轴向位移引起E型电感线圈与缠绕在转子上的电感线圈之间感应电动势变化实现轴向位移测量。可以看出,上述方法均存在传感器结构复杂、安装调试较为困难等问题。
在不改变转子系统结构的前提下,为了尽可能简化传感器安装与测试,笔者提出基于单个位移传感器、单点脉冲宽度响应的转子轴向位移径向测量原理与实现方法:在转子表面粘贴打印条码,利用单个激光光纤传感器开展转子轴向位移的径向测量。测量原理简单,传感器安装及调试方便,为转子轴向位移测量提供了一种新思路。
1 脉冲宽度法位移测量建模
脉冲宽度法位移测量使用的基本条码形状为等腰三角形打印条码,如图1所示。图中:α为等腰三角形条码的底角;w为等腰三角形的底边长;nw为测量区的总长度。

图1 测量条码Fig.1 Measuring bar code
测量条码主要包括两部分:测量区和两边的接口区。测量区由n个等腰三角形依次排列组成,“白色”表明其具有与背景不同的材料特性。为了便于加工、粘贴及周期识别,测量区两边设置接口区。为了保证条码完整包裹转子表面,接口区和测量区长度之和略大于转子周长。
这里采用具有颜色识别功能的激光光纤色标传感器进行三角形条码边缘识别。激光光纤色标传感器通过监测条码颜色输出信号,当检测到白色条码时输出高电平信号,否则输出低电平信号。厚度为h的条码粘贴在待测转子上,位移传感器置于转子径向,中心线垂直于转子的中心线,如图2所示。

图2 传感器布局示意图Fig.2 Schematic diagram of sensor layout
转子工作时,激光光纤型色标传感器输出信号为脉冲信号。转子轴向位移前后传感器输出信号如图3所示。由图中可以看出:z0为转子轴向位移基准距离;TR为转子旋转一圈的周期;当转子轴向位移变化Δz时,传感器两次扫描轨迹发生变化,新轨迹与原轨迹轴向距离差即转子轴向位移量。测量区信号具有一定的局部周期性,转子轴向位移前,t为一个局部周期T内高电平持续时间;轴向位移后,t'为一个局部周期T'内高电平持续时间;转子位移前后局部周期是由条码尺寸确定的,当条码尺寸不变时转子位移前后条码局部周期不变,即T=T'。

图3 转子轴向位移前后传感器输出信号示意图Fig.3 Schematic diagram of sensor output signals before and after axial displacement
由条码中几何关系可得,信号高电平持续时间与局部周期满足
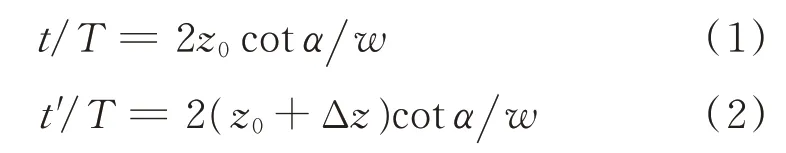
由式(1)和式(2)计算得到转子轴向位移为

式(3)表明,转子轴向位移可通过传感器输出信号和条码尺寸参数计算得到。由式(3)可以看出,转子轴向位移受条码宽度、条码倾角等参数影响,因此需要建立测量模型,探究其对测量结果的影响规律。
2 脉冲宽度法位移测量精度分析
2.1 测量条码建模
对测量条码进行分析时,首先要建立坐标系。所建坐标系O0x0y0z0如图4所示,图中:L1为第1个白色条码的左侧边缘;L1'为第1个白色条码的右侧边缘;L2为第2个白色条码的左侧边缘;L2'为第2个白色条码的右侧边缘;Ln为第n个白色条码的左侧边缘;Ln'为第n个白色条码的右侧边缘;2πR为所贴条码转子周长。
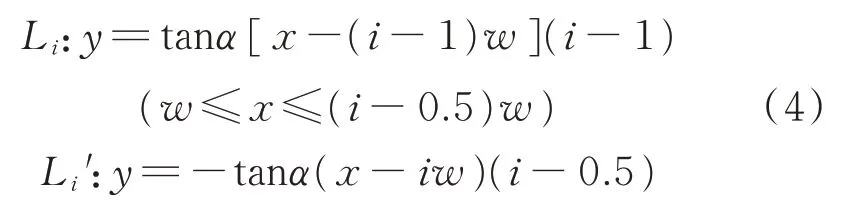
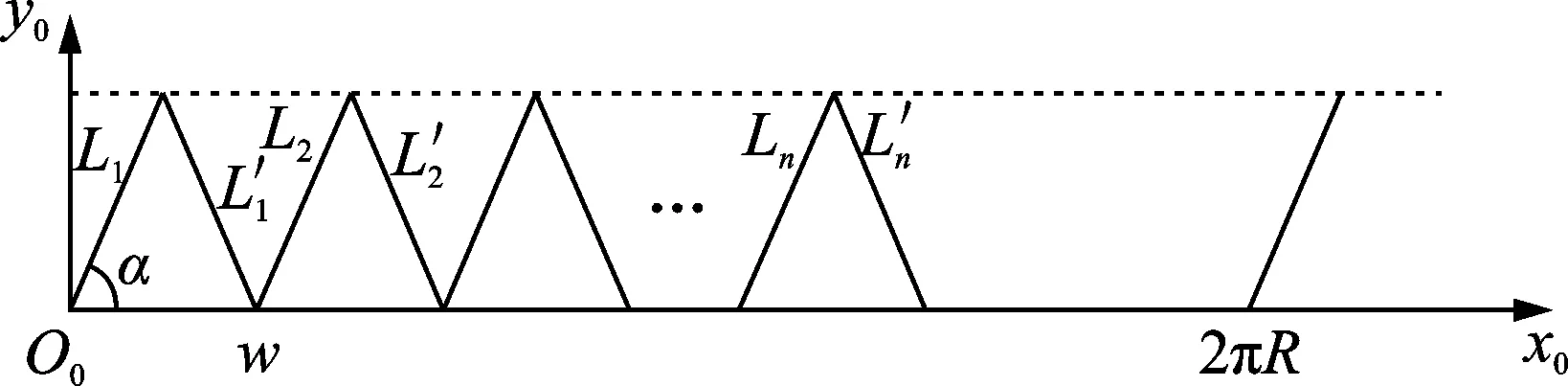
图4 测量条码模型Fig.4 Measuring bar code model

由几何关系可得测量区内,等腰三角形条码边缘方程式可表达为其中:i为条码测量区内条码边缘序号(1≤i≤n且i∈R);Li为第i个白色条码的左侧边缘;Li'为第i个白色条码的右侧边缘。
条码在制作过程中,其边缘受到打印设备、送纸误差等因素影响而非一条直线,这里认为边缘误差服从正态分布,其均值为零,幅值为δ,则实际的边缘可修正为
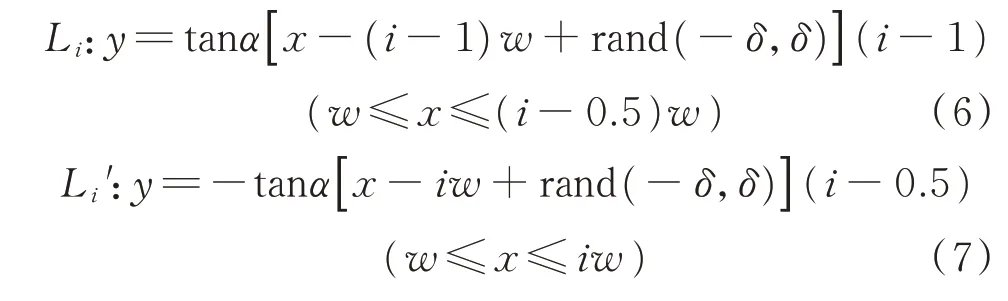
其中:rand(-δ,δ)为区间[-δ,δ]内的随机值。
2.2 待测转子运动模型建立
实际工作过程中,转子运动质心轨迹不是一个点,其受转子倾角、偏心距等装配误差及轴向振动、转动角速度等运动参数影响。在研究转子运动分析时先建立坐标系,转子与基座坐标系如图5所示。图中:O1x1y1z1为转子坐标系;O2x2y2z2为基座坐标系;γ为转子倾斜角;e为转子中心与基座中心偏心距。为了简化计算,这里忽略转子形状误差,将转子看为理想圆柱体,倾斜角、偏心距、转动角速度等运动参数对转子运动的影响采用单独作用结果叠加的方式进行分析。

图5 转子与基座坐标系Fig.5 Rotor and base coordinate system
记e=(ax,ay,az)T,转 动 角 速 度ω相 当 于转 子坐标系O1x1y1z1绕z2轴旋转,轴向振动b和轴向位移z对转子的作用相当于转子坐标系O1x1y1z1沿着z2轴方向平移,作用前后转子上各点的坐标满足
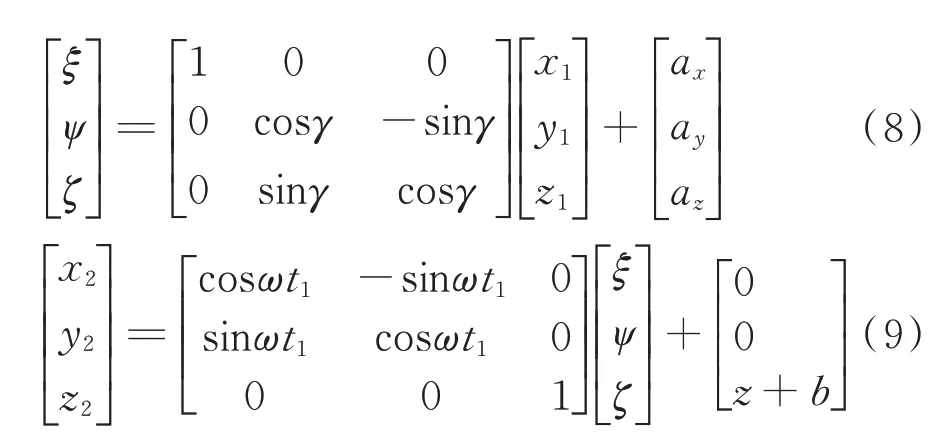
其中:t1为主轴转过的时间;(x1,y1,z1)为转子运动前各点坐标;(ξ,ψ,ζ)为中间变量;(x2,y2,z2)为转子运动后各点坐标。
2.3 测量误差影响因素分析
将所建数学模型采用Matlab编程实现,其主要求解思路如下:①输入条码尺寸参数、转子安装尺寸参数、运转参数等工况参数;②根据条码颜色得到传感器初始输出信号;③根据条码尺寸求解下一采样时刻转子位置;④求解此时传感器输出,保存输出结果,然后循环执行步骤3和4直到预定测量时间。
以某型号转子为例进行分析,参数如表1所示,以表1中各参数值为例,分析条码结构参数、转子工况参数对测量精度的影响,这里采用仿真模型计算的轴向位移与设定位移之间误差作为测量精度的评价标准。
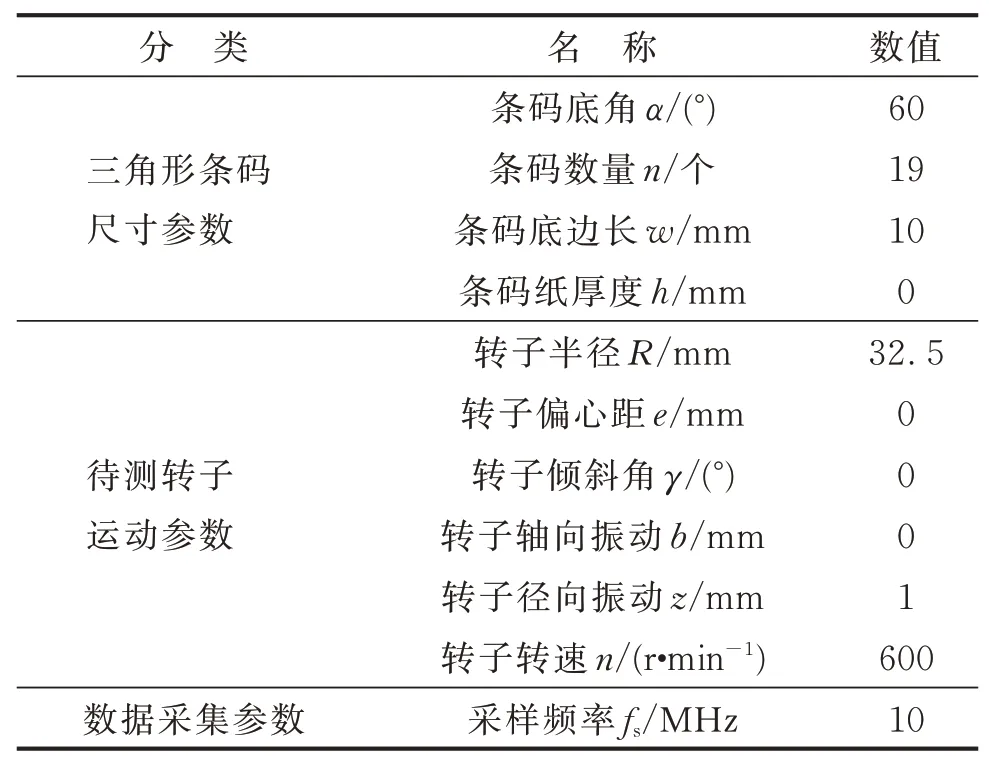
表1 数学模型参数Tab.1 Parameters of mathematical model
2.3.1 转子偏心距
分析转子偏心距对转子轴向位移测量误差的影响时,以表1中所示的各参数为固定参数,改变偏心距的数值,可以得到不同偏心距时的位移计算结果随时间的变化曲线,进而得到转子偏心距与位移计算误差关系曲线,如图6所示。由图中可以看出,偏心距使位移计算结果产生类似正弦规律的周期波动,其转动周期与转子转动周期相同,随着偏心距增大,轴向位移误差增大,偏心距为10μm时,其误差为5μm左右。由于转子制造误差转子偏心距无法消除,转子偏心距影响转子位移测试结果,因此在后续的信号处理中要考虑误差消除问题。
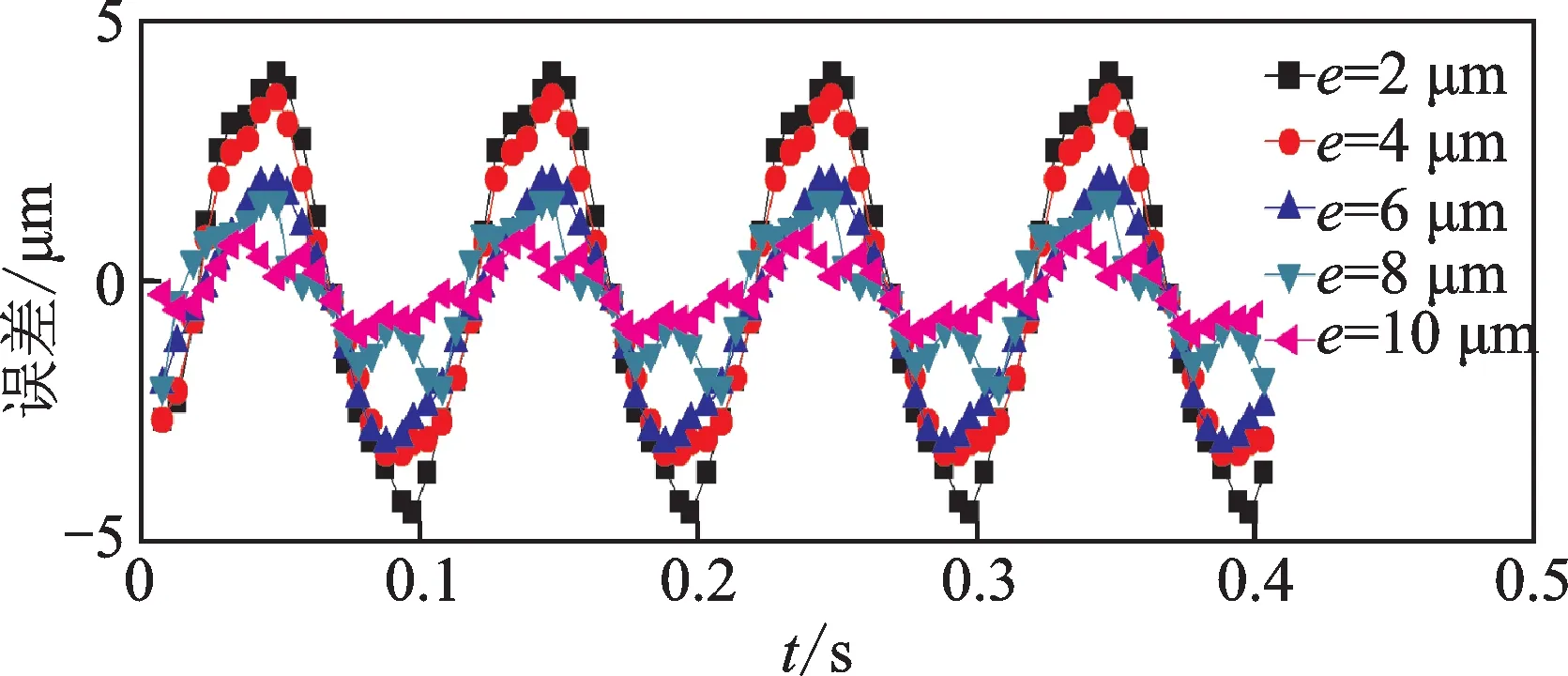
图6 偏心距与位移计算误差关系Fig.6 Relationship between eccentricity and displacement calculation error
2.3.2 条码数量
测量条码数量受待测转子直径影响,转子直径确定,条码数量影响条码宽度,由测试条码几何关系可知条码数量越多条码宽度越小。根据脉冲宽度法位移测量原理,转子转过一个局部周期,传感器输出一次轴向位移。条码数量增加轴向位移响应速度增加。当条码测量区宽度不变,条码数量对转子轴向位移计算结果影响如图7所示。由图7(a)可知,不同条码数量时,位移测量误差的波动范围基本相同,维持在2μm之内;由图7(b)可知,随着条码数量增大,响应时间降低。利用脉冲宽度法进行位移测量时,条码数量几乎不会影响测试精度,但增大条码数量可提高响应速度,实验条件允许时尽量使用条码数量较多的条码。

图7 条码数量对计算结果的影响Fig.7 The effect of the number of bar codes on the calculation results
2.3.3 条码倾角β
由式(3)可知,相同轴向位移下,条码倾斜角度影响传感器输出信号的脉冲宽度,倾角对测试结果的影响如图8所示。由图中可以看出,随着条码倾斜角度增大测试误差增大,测量准确度降低,这是由于相同采样频率下,随着条码倾斜角度增大,条码边缘越陡峭,边缘检测误差越大。相同的测量区长度,条码倾斜角度越小,条码宽度越小,条码制作困难不易粘贴。因此在位移测量中,为提高测量精度,现有制作条件下,尽可能减小条码倾斜角度。

图8 倾斜角度对位移计算误差影响Fig.8 Effect of tilt angle on displacement calculation error
2.3.4 转子直径
为了验证脉冲宽度法测量转子轴向位移适用于不同直径转子,这里分析了不同转子直径下测量误差的影响。待测转子不同在于其直径的变化。若其他相关尺寸不变,转子直径增加时,根据测量条码与待测转子的比例关系可以分为两种情形进行讨论。
1)条码的形状变化比例与直径变化比例相同
此种情形下,转子直径发生变化的同时,条码的宽度发生了相应比例的变化,利用测量模型计算的结果如图9所示。由图9(a)可知,测量误差随着轴径的增大基本不变,其波动范围在0.4μm以内;由图9(b)可知,响应时间与轴径无关,即大尺寸转子与小尺寸转子的测量效果基本相同。
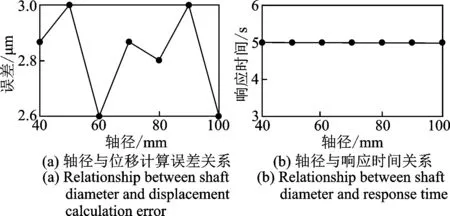
图9 第1种情形下轴径对计算结果的影响Fig.9 Effect of shaft diameter on measurement error in the first case
2)条码的形状变化比例与直径变化比例不同
条码的宽度、倾斜角度不变,根据转子直径变化而改变条码的长度。此情形下,条码测量区条码的尺寸参数不发生变化,只是条码的数量有所不同,这会引起位移计算结果的响应速度发生变化,如图10所示。由图10(a)看出,计算误差都随着转子直径的增大而增大。由图10(b)看出,响应时间随着转子直径的增大而减小。在进行小直径转子位移测量时,由于测量误差较小响应速度较慢需要考虑提高其响应速度。在进行大直径转子位移测量时,由于测量误差较大响应速度较快需要考虑消除测量误差。
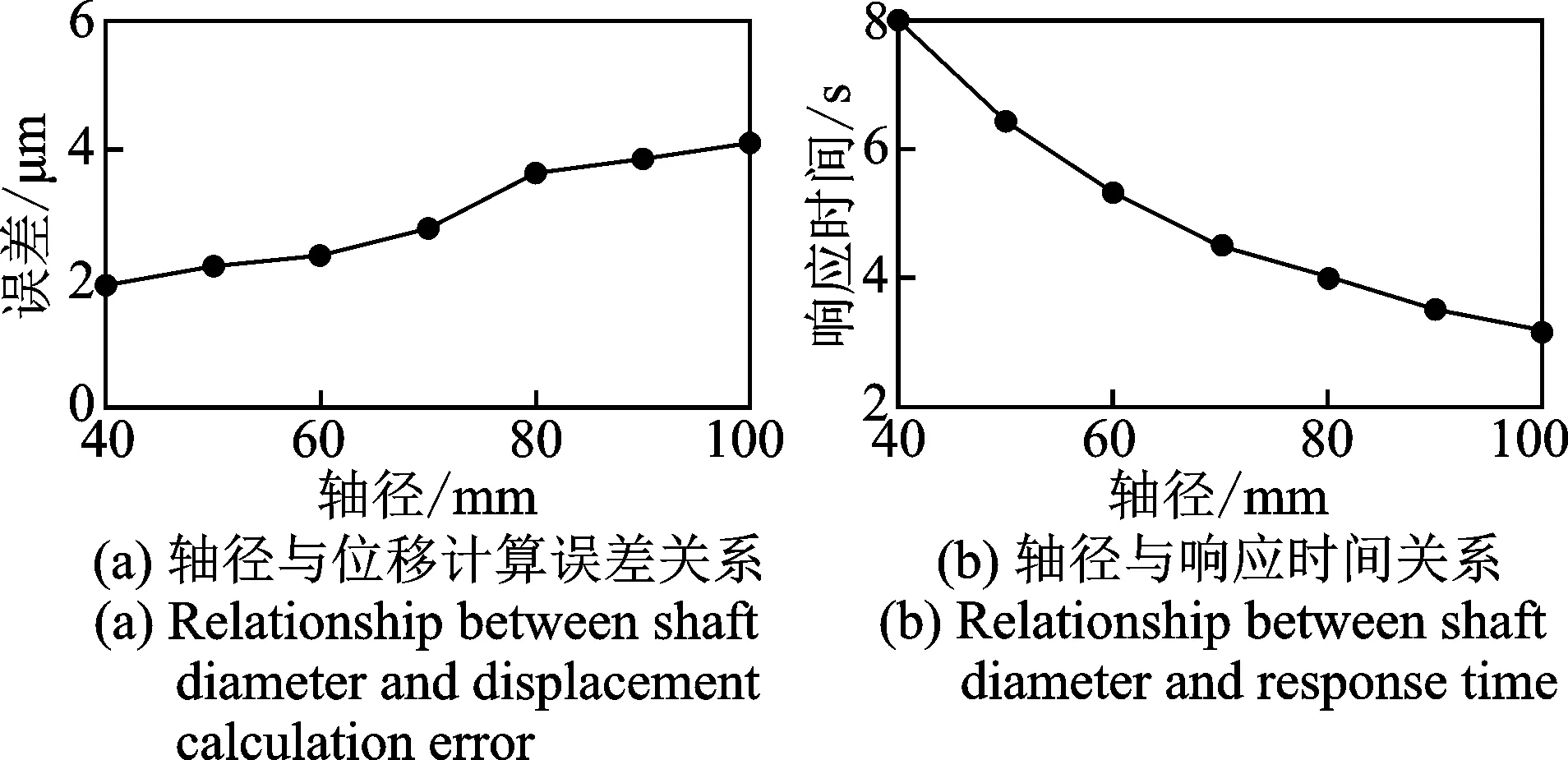
图10 第2种情形下轴径对计算结果的影响Fig.10 Effect of shaft diameter on measurement error in the second case
3 实验测试
3.1 实验装置
测试实验时,文中转子采用电主轴驱动,空气轴支承。激光打印的高精度条码粘贴在转子表面,高精度激光位移传感器及激光光纤传感器固定传感器支架上,如图11所示。其中激光位移传感器及激光光纤传感器的测量精度为±0.5μm。
测量时,由于高精度气浮轴(2 000 r/min下径向 跳动 误 差0.2μm[15])在 加 载 时轴 向 位 移不易 控制,为了保证输入准确的轴向位移,转子相对于传感器的轴向位移,采用移动传感器的方法来实现,如图11所示。通过手轮调节微位移平台移动,使得传感器相对转子产生轴向位移。安装在传感器支架上端的高精度激光位移传感器,得到转子实际轴向位移。安装在支架下端的激光光纤传感器将测得的光信号转化为电压信号,然后经调理电路得到两路时域脉冲信号,根据两次传感器测量信号的脉冲宽度持续时间计算转子轴向位移。通过计算得到的轴向位移与激光位移传感器直接测量得到轴向位移的差值即为测试误差。
3.2 实验结果分析

图11 位移测量实验台Fig.11 Displacement measurement bench
图12 所示为不同转速下条码倾角β对测量误差影响。从图中看出,随着倾角增大,误差增大;转子转速影响误差增大的速度,转速越大误差增大的速度越大;当转子转速为200 r/min时,测量条码倾斜角度对测量误差影响很小,差值为0.78μm。转速为1 000 r/min时,同样倾角变化,误差变化为5.34μm;转速为1 500 r/min时,同样倾角变化,误差变化为6.65μm。同时,同一倾角下,转速越大误差越大。测量误差受测量条码倾角及转子转速联合影响。
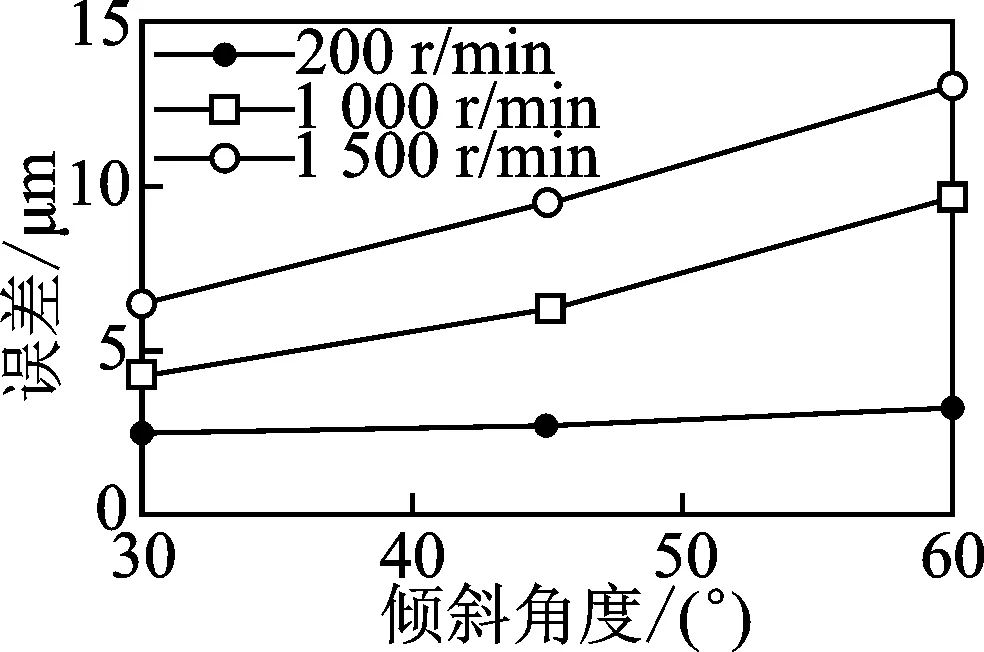
图12 不同转速下条码倾角与测量误差的关系Fig.12 Relationship between bar code inclination and measurement error at different speeds
当条码倾角为45°,条码宽度变化会引起条码数量的改变。如图13所示不同转速下条码宽度对误差的影响规律,由图中可以看出,同一转速下条码宽度对误差影响较小。
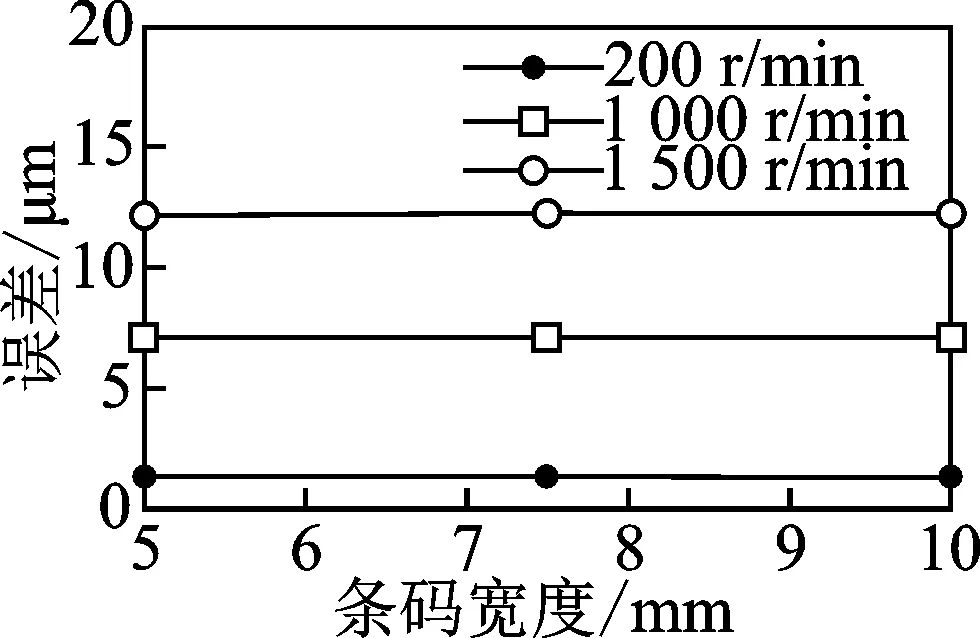
图13 不同转速下条码宽度与测量误差的关系Fig.13 Relationship between bar code width and measurement error at different speeds
综上所述,本方法在保证测量范围的前提下,由于条码宽度对测量误差的影响不大,在转子直径和测量区长度确定的情况下,可以通过减小倾斜角度来提高转子位移的测量误差。
4 结论
1)针对转子轴向位移径向测量中存在转子结构改变、传感器安装调试复杂等问题,提出了一种结合打印条码和光学色标传感器的轴向位移径向测量方法,结合理论模型及实验验证了该方法的有效性,为转子轴向位移的径向测量提供了新思路。
2)通过建立模型探讨了条码几何参数及转子工况条件等对测试结果的影响规律,条码数量增大转子位移误差基本不变响应速度增加;条码倾斜角度越大转子轴向位移的误差越大;条码参数随着转子直径同比例增大时,转子轴向位移误差波动范围为0.4μm,响应速度基本不变;条码数量增多其他参数不变时,转子直径增大时,转子轴向误差增大,响应时间降低。
3)理论和精密气浮轴系实验测试表明:低速下转子轴向位移测量误差较低,能够满足工程测量精度。后续研究将进一步提升对条码边缘检测精度,提高在高速情况下的测试精度。

