基于时空状态网络的电动物流车辆路径优化方法

杨森炎，宁连举，商攀

(1.北京邮电大学，a.现代邮政学院(自动化学院)，b.经济管理学院，北京100876；2.北京交通大学，交通运输学院，北京100044)

0 引言

电动车辆具备低能耗、低排放、低噪声等优势，已广泛用于城市“最后一公里”物流配送过程。由于电池续航里程有限，电动车辆需要在途中补充电量。充电设施不足导致车辆绕路或排队充电现象[1]。为提高电动物流车辆服务效率，学者们基于经典的车辆路径问题，考虑充耗电过程、电池容量等限制条件，提出电动车辆路径优化问题(EVRP)。Schneider 等[2]假设充电量与充电时间呈线性关系，研究带时间窗的EVRP问题(EVRPTW)，设计了可变邻域搜索算法与禁忌搜索结合的混合启发式求解算法。Montoya等[3]提出分段线性逼近方法，研究非线性充电过程的EVRPTW 问题。Goeke 等[4]研究电动车辆和内燃机车混合下的EVRPTW问题。Felipe等[5]研究部分充电策略和不同充电技术下的电动车辆路径规划和充电决策优化方法。Keskin等[6]对比了部分充电和完全充电策略下的路径优化方案。Hiermann 等[7]研究考虑不同车辆配置的EVRPTW 问题，提出基于自适应大邻域搜索的混合启发式算法，通过智能局部搜索改进路线。

既有关于EVRPTW 问题的研究在车辆行驶、充耗电过程、充电站能力等方面考虑的约束条件较为复杂。传统的基于物理运输网络的建模方法难以充分考虑客户需求和电动车辆运行状态的时空特性，需要设置时间、空间、载重状态、电量状态等多种类变量，建立大量的复杂约束条件以描述变量之间的相互关系，因此模型结构较为复杂。常采用的智能算法虽然通用性强，时效性较高，但难以从理论上保证解的质量。

近年来学者们提出采用时空网络的建模方法求解车辆路径优化问题，通过系统离散化方法处理复杂约束，可以有效简化模型，降低问题的求解难度。Mahmoudi等[8]提出时空网络的建模框架，求解城市交通场景下接送乘客的车辆路径问题。Yang等[9]基于离散的时空状态网络表示方法，对考虑混合取送的物流车辆路径优化问题进行建模和求解。

本文运用离散的时空状态网络方法，研究考虑充电策略的电动物流车辆路径优化问题，对电动物流车辆路径规划和充耗电过程进行离散化表示，建立多商品网络流优化模型，在时间、空间和状态维度上对电动物流车辆路径以及充电策略实现同步优化，并设计基于增广拉格朗日松弛技术的求解算法，将原问题分解为一系列规模较小的最短路径子问题，可以快速找到可行解。

1 模型构建

1.1 问题描述

本文采用部分充电策略，即车辆中途只需补充支撑其完成剩余配送任务的部分电量，可以减少不必要的充电等待时间。考虑电池容量、车辆承载能力、充电站能力、客户服务时间窗、路网空间结构等约束，优化客户的服务顺序、充电站点选择及单次充电时间。模型假设如下：

(1)配送中心车辆充足，车辆出发时处于满电状态，完成配送后返回到原配送中心；

(2)车辆的耗电量与行驶时间成正比，当剩余电池容量低于最小阈值时需补充电量；

(3)充电速率固定，充电量与充电时间满足线性关系；

(4)不考虑路网交通状态的影响，车辆保持匀速行驶。

1.2 符号定义

(1)集合和元素

N——物理网络节点集合；

T——时间点集合；

V——电动车辆集合；

P——客户集合；

S——充电站点集合；

W——车辆剩余载货量状态值集合；

L——空间路段集合，L={(i,j)|i∈N,j∈N}

Av——车辆v对应的时空状态弧集合，Av={(i,j,t,t′,w,w′,e,e′)|i∈N,j∈N}；

ψp,v——车辆v服务客户配送需求的弧集合，ψp,v⊆Av；

ψs,v——车辆v在充电站充电的弧集合，ψs,v⊆Av；

i,j,j′,j″——节点编号，i,j,j′,j″∈N；

t,t′,t″——时间编号，t,t′,t″∈T；

v,v′——车辆编号，v,v′∈V；

p——客户编号，p∈P；

s——充电站编号，s∈S；

w,w′,w″——剩余载货量状态值，w,w′,w″∈W；

e,e′,e″——剩余电量状态；

(i,t,w,e)——时空状态点；

(i,j,t,t′,w,w′,e,e′)——时空状态弧；

o——配送中心节点；

to,v——车辆v离开配送中心o的时间；

t′o,v——车辆v返回配送中心o的时间；

wo,v——车辆v离开配送中心o的剩余载货量；

w′o,v——车辆v返回配送中心o的剩余载货量；

evo——车辆v离开配送中心o的剩余电量；

e′o,v——车辆v返回配送中心o的剩余电量。

(2)参数

Emin——最小剩余电量阈值；

Emax——电池容量；

ξs——充电站s的充电能力，即最多可允许同时充电的车辆数量；

γs——充电站s的充电速率；

κv——车辆v的耗电速率；

χv——车辆v的最大承载能力；

[te,p,tl,p]——客户p的服务时间窗，其中，te,p为可服务p的最早时间，tl,p为可服务p的最晚时刻；

c(i,j,t,t′,w,w′,e,e′)——时空状态弧(i,j,t,t′,w,w′,e,e′)的配送成本。

(3)决策变量

y(i,j,t,t′,w,w′,e,e′),v——若车辆v经过弧(i,j,t,t′,w,w′,e,e′)则为1，否则为0。

1.3 构建离散时空状态网络

时空状态网络具有时间、空间和状态3 个维度。考虑到配送过程同时受车辆承载能力和电池续航能力限制，对状态维度进行扩展，用状态向量[w,e] 表示车辆的载货量状态和剩余电量状态。车辆经过节点i的时空状态可以用[i,t,w,e] 表示，即车辆在t时刻行驶到节点i，载货量w，剩余可用电量e。时空状态网络中任意两个相邻节点[i,t,w,e]和 [j,t′,w′,e′]之间存在一条时空状态弧(i,j,t,t′,w,w′,e,e′)，共有4种不同类型的时空状态弧，分别是运输弧、充电弧、配送弧及等待弧。需要根据以下规则构建时空状态网络。

(1)针对EVRPTW 问题，对时间和车辆载货状态维度进行离散化，构建时空状态点集合。

(2)基于物理空间网络节点之间的邻接关系，增加离散的时间和状态维度，建立时空状态弧集合A，包括运输弧集合ψT、充电弧集合ψS、配送弧集合ψP和等待弧集合ψW，即A=ψT⋂ψS⋂ψP⋂ψW，具体如下：

添加运输弧，对于任意i,j∈N，t∈T，Ti,j,t为t时刻路段(i,j)的运输时间，车辆耗电速率是κv，添加 (i,j,t,t′,w,w′,e,e′)到ψT，且满足关系：t′=t+Ti,j,t,w′=w,e′=e-κv·Ti,j,t。

添加充电弧，对于任意s∈S,t∈T，充电站s的充电速率为γs，添加(s,s,t,t+1,w,w′,e,e′)到ψS，且满足关系：w′=w,e′=e+γs×1。

添加配送弧，对于任意t∈T，p∈P，客户p位于弧(ip,jp)上，其配送需求为np，Tp,t为t时刻服务客户p所需的时间，车辆耗电速率为κ′v，添加(ip,jp,t,t′,w,w′,e,e′)到ψP，且满足关系 ：t′=t+Tp,t,w′=w-np,e′=e-κ′v·Tp,t。

添加等待弧，对于任意i∈N，t∈T，添加(i,i,t,t+1,w,w′,e,e′)到ψW，且满足关系：w′=w,e′=e。

(3)对于任意一条时空状态弧a∈A，设置对应的成本ca。

以8点配送网络为例，客户位于空间网络上相邻两个节点之间，如图1所示，假设电池最大容量Emax=10，最小电量阈值Emin=2。电动车辆从配送中心出发时处于满载和满电状态，为5位客户配送货物，当e低于Emin时，需要选择充电站进行充电。最优路径节点顺序是“1→2→4→5→7→3→1”，剩余载货量和电量的时空变化过程如图2所示。车辆在节点7 完成充电的过程可以用两个充电弧(7,7,4,5,3,3,2,6)和(7,7,5,6,3,3,6,10)表示。车辆完成对客户1 的配送服务过程可以用配送弧(2,4,1,2,8,7,8,6)表示。车辆在完成客户的配送服务之后载货量和剩余电量均降低。

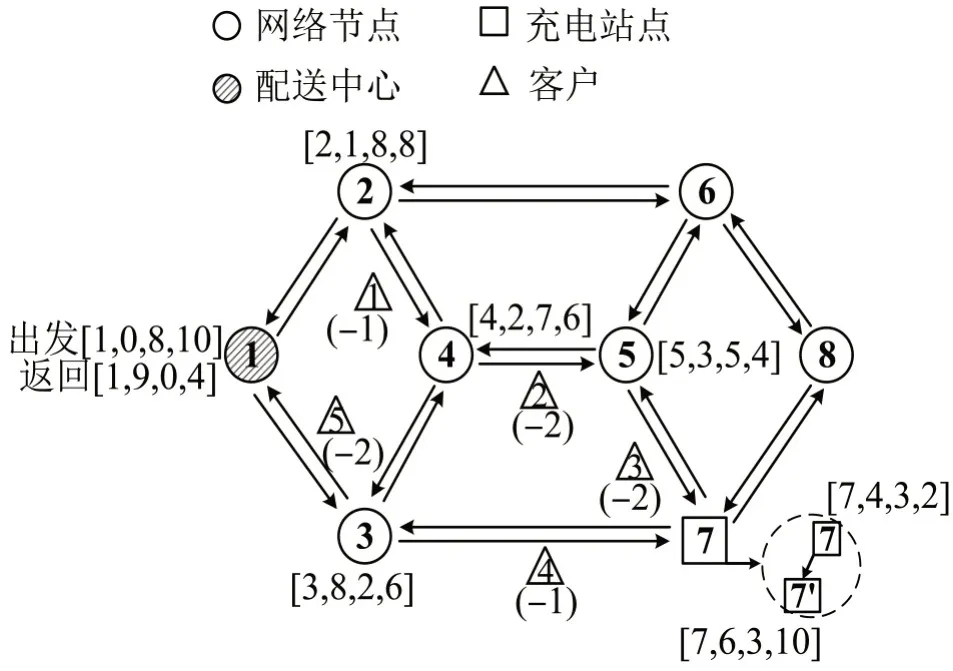
图1 配送网络示意图Fig.1 Diagram of distribution network

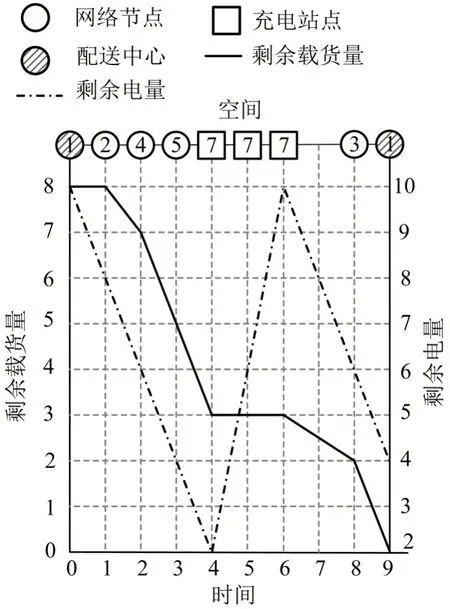
图2 电动物流车行驶过程中的时空状态变化Fig.2 Spatial-temporal state changes during electric logistics vehicle driving

客户服务时间窗口、车辆承载能力和电池容量等实际约束条件以及时间、载货量和电量状态的更新直接嵌入时空状态网络的构建过程，缩减算法的搜索空间，提高计算效率。具体如下：

①客户配送服务时间窗约束，车辆需要在客户p的服务时间窗[te,p,tl,p] 内配送货物，即配送时间范围是te,p≤t≤tl,p。

②车辆承载能力约束，任意车辆v在任意时刻t的剩余载货量wv,t不能超过其承载能力χv，即0 ≤wv,t≤χv。

③电池容量约束，任意车辆v在任意时刻t的剩余可用电量状态ev,t不小于阈值Emin，且不超过电池容量Emax，即Emin≤ev,t≤Emax。

④时间更新规则，对于任意时空状态弧(i,j,t,t′,w,w′,e,e′)，车辆经过相邻节点的时间关系满足t′=t+Ti,j,t。

⑤电量消耗过程，对于任意运输弧(i,j,t,t′,w,w′,e,e′)，车辆经过相邻节点的能量更新规则为e′=e-κv·Ti,j,t。

⑥充电过程，对于任意充电弧(i,i,t,t+1w,w′,e,e′)，车辆的能量更新规则为e′=e+γs×1。

1.4 多商品网络流优化模型

以最小化总配送成本为目标，针对EVRPTW问题，构建多商品网络流优化模型为

式(1)为目标函数，最小化总配送成本；式(2)～式(4)为流量平衡约束，式(2)保证车辆从配送中心出发，式(3)保证车辆最后返回配送中心，式(4)保证每条路径任意中间节点的输入流和输出流平衡；式(5)确保每位客户的配送需求被服务；式(6)保证每个充电站同时充电的车辆数不超过其充电站能力；式(7)为决策变量。

为保证使用尽可能少的电动车辆，设置从配送中心直接返回到配送中心的虚拟弧，虚拟弧的成本为0。对于无需完成配送任务的车辆，直接通过虚拟弧返回配送中心，不会进入正常的服务网络。

时空状态网络建模方法是在传统物理网络上增加了时间和状态维度，可以清晰地刻画车辆运行过程中时间变化、空间变化及状态转移之间的耦合关系，构建复杂场景下的网络流优化模型，适用于解决带有时间窗约束或者时变运输网络优化问题。虽然该方法可以显著减少EVRPTW 问题的变量种类和约束数量，但是求解上述0-1 整数规划模型仍然属于NP-hard，时间和状态维度的离散化导致搜索空间增大，在计算复杂度上存在较大的挑战。

2 算法设计

2.1 模型分解

为使模型简洁，用a表示时空状态弧(i,j,t,t′,w,w′,e,e′)。采用拉格朗日松弛方法，把上述整数规划模型的式(5)和式(6)松弛到目标函数式(1)中，得到拉格朗日松弛模型(LR)为

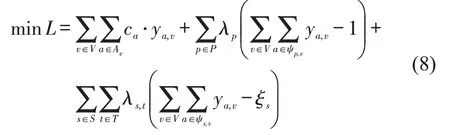
保留约束条件式(2)～式(4)和式(7)。

分解可得单辆车的LR子模型为

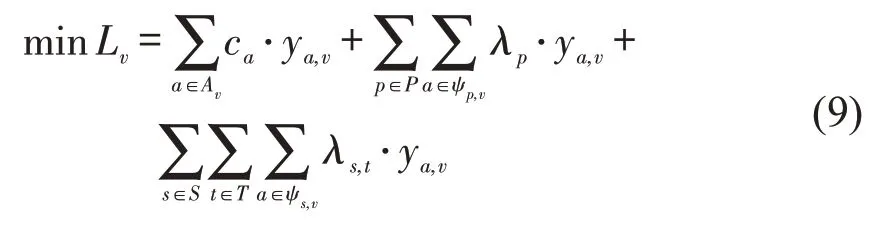
化简为

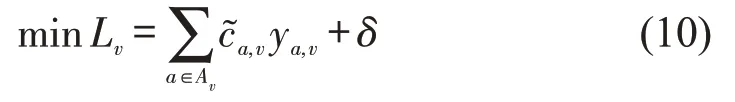
成本为

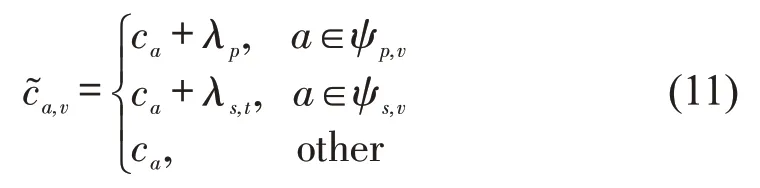
该问题是标准最短路径子问题，具有相同的拉格朗日乘子λp和λs,t。每次迭代，相同车辆会倾向于选择服务同一客户，导致解的对称性问题，影响求解效率。为克服对称性问题，在LR 模型的基础上增加一个增广二次项，构建增广拉格朗日松弛模型(ALR)为

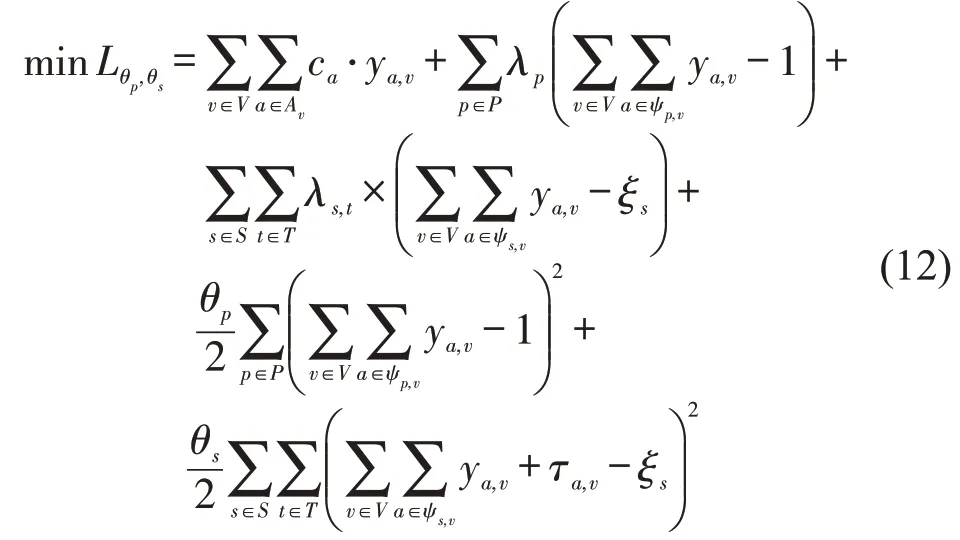
式中：θp和θs为惩罚参数。二次惩罚项的引入导致ALR模型难以分解。为把ALR模型分解为易求解的子模型，对模型进行线性化处理。定义αp,v和βs,t,v为

式中：αp,v为客户p除了车辆v之外被其他车辆服务的总次数；βs,t,v为除了车辆v之外在充电站s充电的总车辆数。车辆v对应的子问题目标函数为

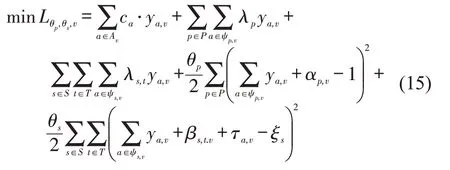
由于ya,v是0-1 变量，二次项等价于，进一步化简为

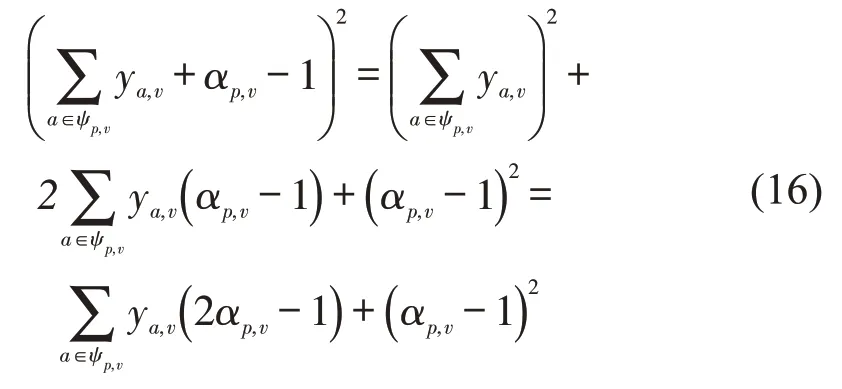
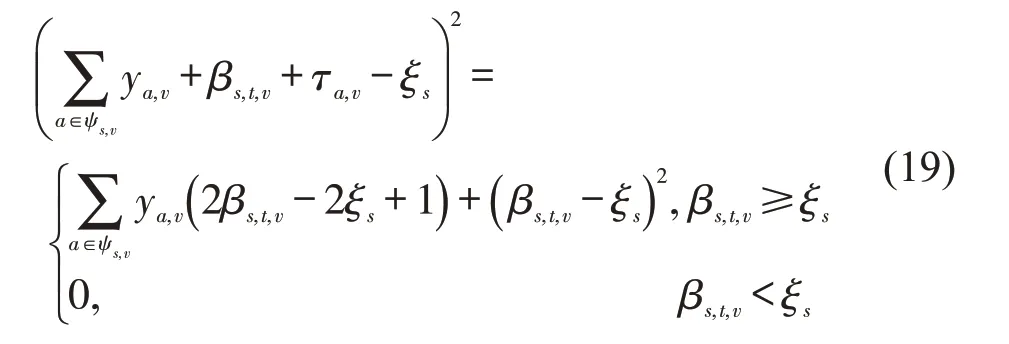
根据式(16)和式(19)，式(15)可进一步化简为

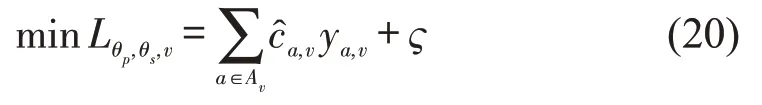
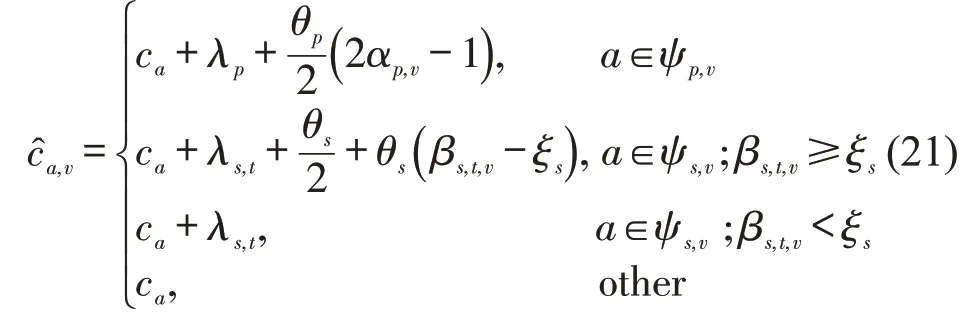
式中：ς为常数项。

2.2 求解算法

采用块坐标下降法(BCD)的分解优化框架，嵌入前向动态规划(DP)算法，对ALR 模型分解得到的最短路径子模型进行循环迭代求解。在BCD框架中，变量和约束条件按车辆被分为若干个模块，针对每个模块依次最小化目标函数[10]。假设配送中心有M辆电动车，编号m=1,2,…,M，任意车辆vm对应的时空状态弧变量集合设为Ym，M辆电动车的时空状态弧变量总集合设为Y。ALR 模型的目标函数为

式中：y∈Y=Y1×Y2×…×Ym⊆Rn，Ym⊆Rnm，变量y1,y2,…,yM依次更新公式为

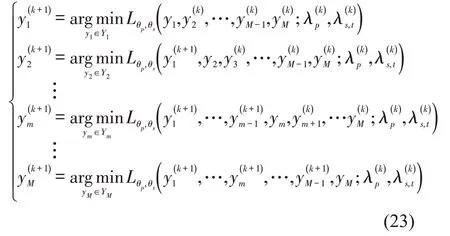
在第k+1 次迭代，为了优化第m辆电动车的路径，完成前i-1 辆电动车的时空状态路径优化后，更新车辆路径方案，后M-m辆车的路径仍然保持第k次迭代的优化方案惩罚参数θp和θs分别是拉格朗日乘子和的更新步长，即

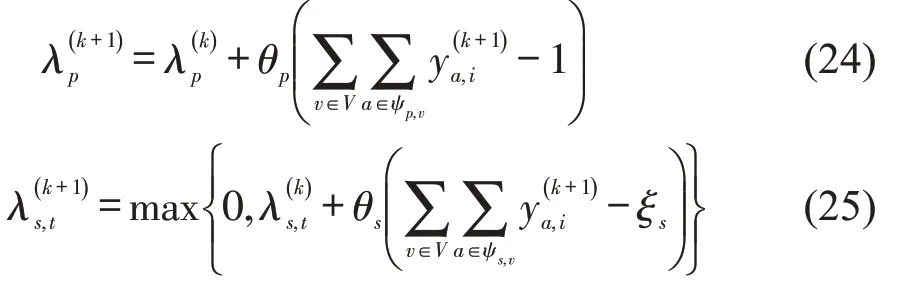
基于ALR 的方法可以通过增设二次惩罚项，克服LR 方法存在的对称性问题，提高算法的收敛速率；另一方面，每次迭代计算最优上界和下界的间隙GGAP，可以从理论上评估可行解的质量，具体步骤如下。

Step 1 初始化

Step 2 计算ALR模型的下界解

Step 2.1 求解子模型

按式(21)更新成本c^a,v，不考虑充电站的充电能力约束，使用DP 算法，按式(23)的迭代方式，依次优化单辆车的配送路径。

Step 2.2 计算下界解，更新最优下界值

根据Step 2.1 得到的车货分配方案，计算下界解，规则为：若某些客户被多辆车服务，则仅指派一辆车配送即可；若存在部分服务需求没有被满足，则重新指派一辆车完成服务。

计算下界值，并按更新最优下界B*LB。

Step 3 计算ALR模型的上界解

Step 3.1 求解子模型

Step 3.2 计算上界解，更新最优上界值

根据Step 3.1 得到的车货分配方案，计算上界解，规则同Step 2.2。

计算上界值，并按更新最优上界B*UB。

Step 4 评估解的质量

计算B*UB和B*LB之间的最优间隙GGAP为

GGAP值越小，解的质量越好。

Step 5 更新拉格朗日乘子

采用次梯度方法，按式(24)和式(25)更新拉格朗日乘子λp,λs,t。

Step 6 结束终止条件

若k到达最大迭代次数K，终止算法，并输出，B*UB，GGAP和最优上界解；否则，返回Step 2，k=k+1，继续迭代。

Step 2.1和Step 3.1的DP算法采用了隐枚举的思想，尽早去除不满足约束条件的变量取值组合，直至找到一个满足条件的可行解，并记为当前最优的可行解，计算其目标函数值。后续迭代得到的可行解的目标函数值与当前最优值进行比较，对可行解的质量进行改进。

求解最短路径子问题的过程是上述ALR 算法最耗时的环节。 整个算法的复杂度是O(K×nV×nL×nT×nW)，其中，K为迭代次数，nV为电动车辆数，nL为空间路段数，nT为离散的时间点数，nW为车辆承载能力。采用时空状态网络的建模方法需要确定合适的离散精度，若离散的时间、空间及状态精度过高，时空状态网络规模过大，会影响算法的计算效率；若离散精度设置过小，会影响模型的精确性。

3 算例分析

算法执行的硬件环境为Intel(R)CPU(TM)i7-7700 CPU @ 3.60 GHz，内存为16 GB。软件环境为Windows 10系统，使用Python编写求解算法。

3.1 算法分析

基于Sioux Falls 网络构建测试算例，如图3所示，共有24个节点和76条路段，其中，节点11设为配送中心，节点1、2、8、13、15、18、23分别设为充电站s1,s2,s8,s13,s15,s18,s23，每条路段上标记的是行程时间。电动车辆从配送中心出发时均处于满载(w0=8)和满电状态(e0=30)。充耗电过程的相关参数设置为：最小剩余电量阈值Emin=3，最大电池容量Emax=30，充电速率γ=10，耗电速率κ=1，充电站能力ξ=2。

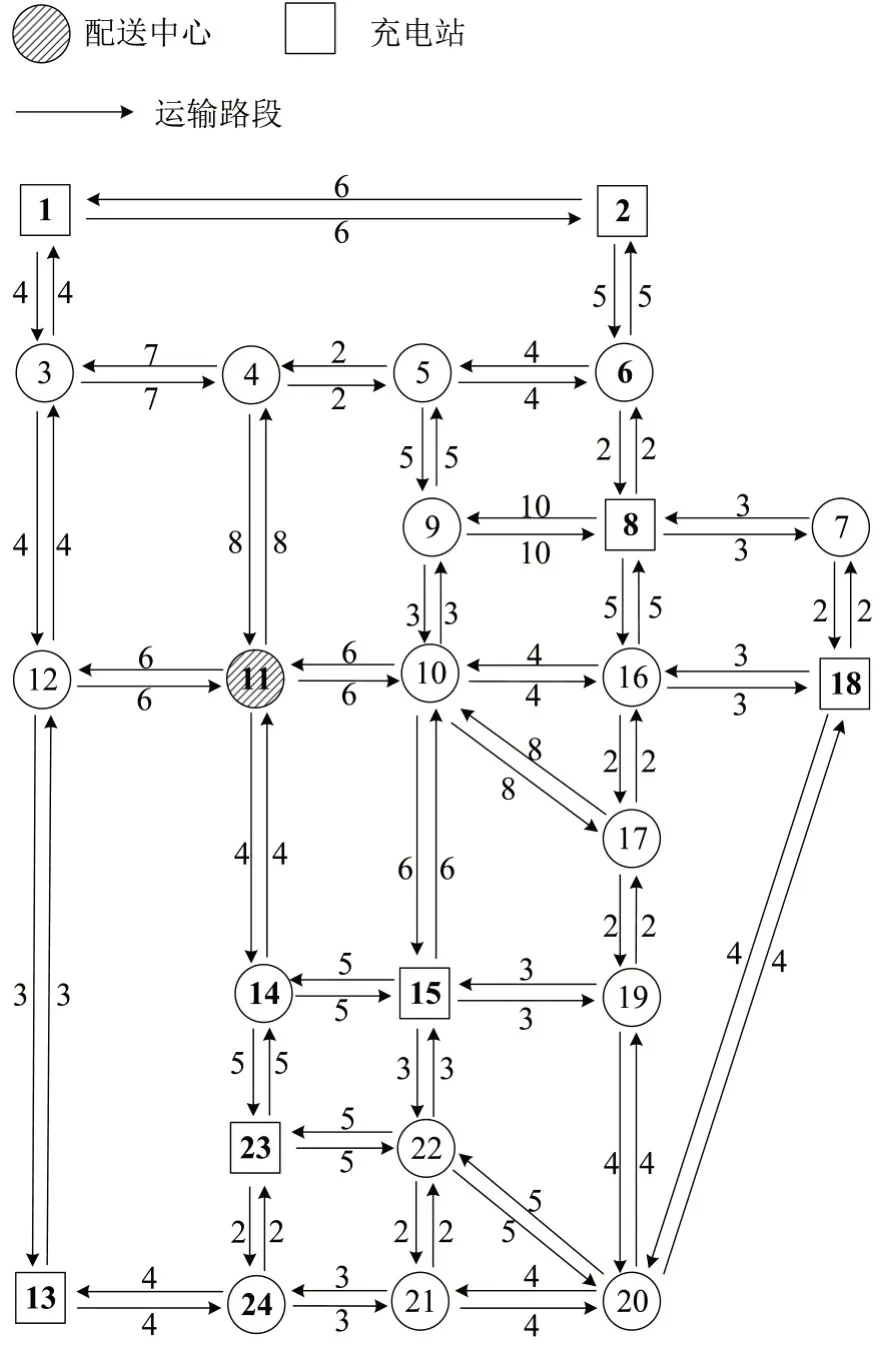
图3 Sioux Falls网络Fig.3 Sioux Falls network

为测试算法求解不同规模算例的性能，设置两组实验，分别为24位客户和50位客户，得到电动车辆和充电站使用方案如表1所示。24 个客户的算例需使用6 辆车和4 个充电站(s8,s13,s15,s23)，其余充电站均未有车辆充电。50 个客户的算例需使用10 辆车和6 个充电站(s2,s8,s13,s15,s18,s23)。客户数量增大需要调用更多的电动车辆完成配送任务，也会提高充电站的利用率。

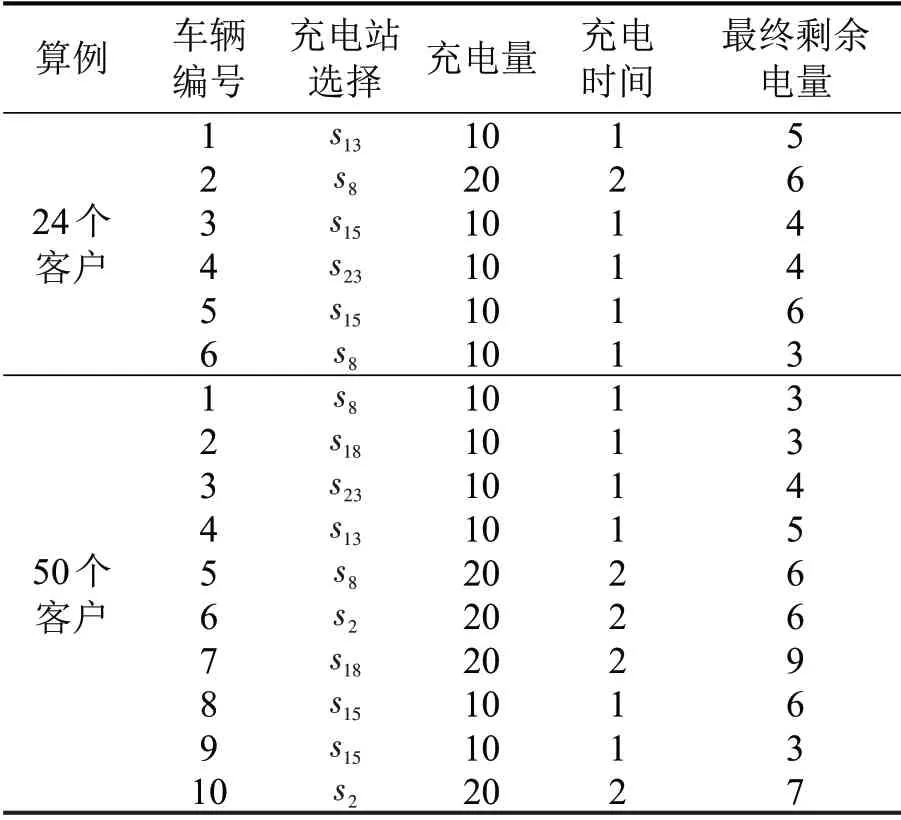
表1 优化方案Table 1 Optimization scheme

两组不同规模算例的实验结果如表2所示，可以看出，算法能够在有限的迭代次数内收敛，计算效率较高。最优上界值与最优下界值之间的GGAP较小，表明计算得到的可行解已接近最优解，质量较高。客户数量越多，服务客户需要的电动车辆越多，算法收敛需要迭代的次数越多，计算效率有所降低，但仍然可以较快地找到可行解。在24 个客户算例中，算法迭代次数K设为100，ALR 算法每次迭代得到的最优上界和下界变化如图4所示，迭代43次后，最优上界值、最优下界值以及两者之间的GGAP均保持不变，即算法收敛到较优的解。

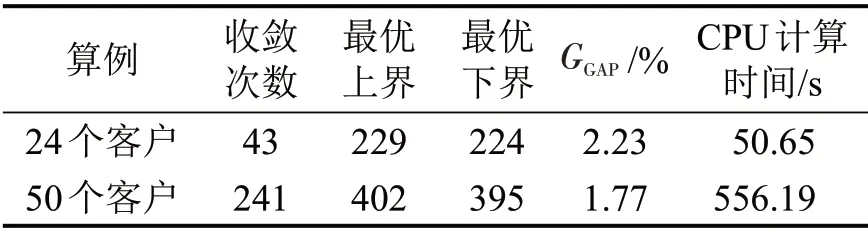
表2 不同规模算例的实验结果Table 2 Experimental results of different-scale instances

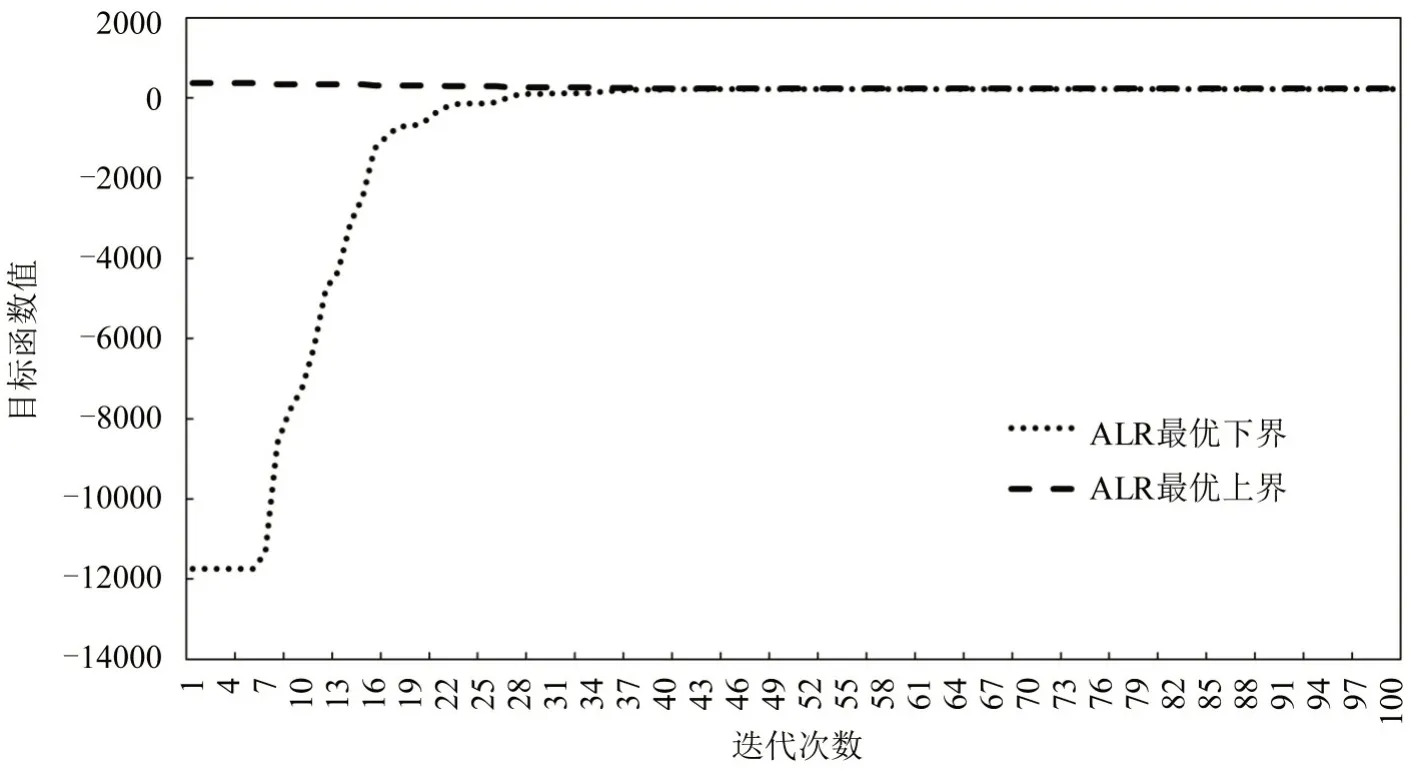
图4 ALR最优上界和下界变化Fig.4 Variations of ALR best upper and lower bounds

3.2 参数灵敏度分析

(1)充电速率

把24 个客户算例设为基准算例，充电速率γ调为5，其余参数保持不变。算法迭代63 次后收敛，CPU计算时间为79.51 s。充电速率降低使电动车辆在充电站的充电时间变长，由于客户服务时间窗是固定的，导致车辆路径和充电优化方案整体上发生较大变化。如表3所示，与基准算例(γ=10)相比，总时间成本增大7.9%，总充电量提高14.3%，总充电时长显著增大。

表3 充电速率的影响Table 3 Influence of recharge rate

(2)充电站能力

在基准算例的基础上，充电站能力ξ调为1。算法迭代62 次后收敛，CPU 计算时间为74.93 s。如表4所示，与基准算例(ξ=2)相比，总时间成本有所降低，总剩余电量增大，故充电站能力参数也会影响车辆整体的路径规划和充电决策。

表4 充电站能力的影响Table 4 Influence of recharging station capacity

4 结论

本文综合考虑了电动物流车辆路径规划、客户配送服务需求及充耗电过程，基于高维的离散时空状态网络，构建了多商品网络流优化模型，设计了基于ALR 和BCD 技术的分布式优化算法，基于Sioux Falls 网络测试算例，验证了算法的时效性和可靠性，并得出以下结论：

(1)时空状态网络建模框架可以有效减少变量类型和耦合约束，简化模型结构；

(2)ALR 模型中惩罚项的引入可以克服LR 解的对称性问题，加快算法的收敛速率，且最优上下界的计算可以评估可行解的质量。

(3)考虑部分充电策略的电动车辆路径规划可以降低能源消耗和运营成本，在时间、空间和状态维度上实现电动物流资源的优化配置。