考虑均衡性的城市轨道交通线路负荷水平评估研究

王敏，毛保华*，杨彦强，史芮嘉，王瑜琼

(1.北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京100044；2.北京市城市规划设计研究院，北京100045)

0 引言

在《辞海》中，负荷的一种解释是“承载”。城市轨道交通系统所承载的对象为客流，客流即为负荷。从数值上说，负荷水平包括绝对量和相对量两个层面：客流规模是负荷水平的绝对值，客流规模与系统(设备)运输能力(承载能力)的匹配情况是负荷水平相对值，本文重点关注的是负荷的相对水平。现实中，由于客流时空动态分布的不均衡特性[1]，运营商所提供的列车开行方案难以精确匹配客流需求，表现出线路负荷分布不均衡等问题。例如，列车在中心城区满载率高而在其他区间运力相对浪费；在潮汐客流条件下，表现在时间和空间维度的负荷水平相差较大等。合理地评估线路负荷水平，对优化运力和改善服务水平具有重要现实意义。

既有研究提出一系列指标评估线路运输能力与客流需求的匹配程度，例如断面满载率、线路列车平均满载率[2]。施云惠[3]提出考虑区间拥挤度惩罚系数的列车综合平均满载率指数，作为评价线路层拥挤度指数的指标之一。张铭[4]等提出用输送能力与客流量的比值来刻画换乘站的运能匹配度，数值越小，表示客流拥堵越严重。这些指标主要体现了线路运输能力与客流匹配的平均程度。

然而，单一均值性指标仅在一定程度上体现线路负荷水平的整体情况，不能反映线路内部分布的偏差。这是因为均值性指标相近时，由于列车开行方案或客流条件发生变化，各区间的列车负荷可能存在较大差异。以文献[5]的第四章大小交路模型和早高峰算例为例进行说明，假设大、小交路列车发车频率均为10 对·h-1，编组为8A，其他参数取值不变。研究发现，当小交路区段分别是区间2～19，5～22，6～23 和7～24 时，4 种交路方案下的线路列车平均满载率r分别是31.52%，31.82%，31.66%和31.55%，最大相差只有0.3%。但是从分布结果看，4 种交路方案得到的大、小交路列车最大满载率相差33.49%，41.17%，57.09%，68.98%。

在描述城市轨道交通系统客流不均衡的指标方面，国内外学者应用基尼系数、标准差率等统计学指标。Hörcher[6]采用基尼系数表征客流需求的不均衡，代洪娜[7]、肖雪梅[8]等提出基于基尼系数定量化评价路网流量分布和城市轨道交通客流分布均衡性的方法。史芮嘉[9]应用标准差率、Geary's C等指标分析线路输送能力利用的特点。但是，关于线路负荷水平的评估及影响因素分析仍缺乏深入研究。

综上，城市轨道交通线路负荷水平涵盖了运输能力与客流的匹配大小与均衡程度两个方面，应包括常见的均值性指标和描述个体负荷分布的两类指标。为此，本文在既有研究的基础上，提出线路负荷均值指标、标准差率指标的二维评价指标，建立线路负荷水平评估模型，并研究客流、列车开行方案等因素对负荷水平的影响。

1 线路负荷水平评估指标模型

将列车作为构成线路负荷的基本单元，每列列车在每个区间的负荷值作为一个样本点。使用研究时段内所有样本的均值性指标表征线路负荷的平均水平，利用所有样本的标准差率指标刻画线路负荷的分布偏差。

研究时段内，线路的f方向s断面第k列车的负荷(即第k个样本点)为

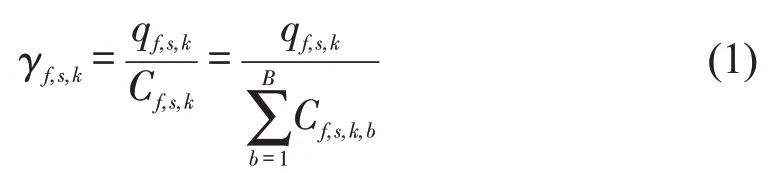
式中：f为线路上行和下行，f∈{0,1}；Kf,s为列车在f方向s断面运行的列车数量，为运输组织方案指标，k∈{1,2,…,Kf,s} ；S为线路断面数量，s∈{1,2,…,S}；qf,s,k为在车人数；Cf,s,k为列车定员；Cf,s,k,b为列车第b节车厢定员，列车为B节编组。

1.1 负荷均值指标

为反映每个样本对线路负荷水平的贡献程度，采用加权计算方法，以单一方向的计算为例(下同)，得到在研究时段内线路f方向负荷水平均值为

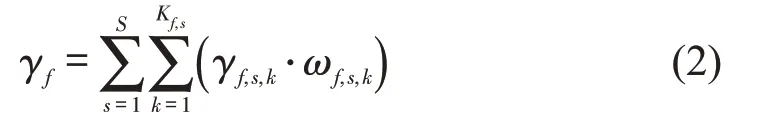
式中：ωf,s,k为权重，权重值一般由区间特征确定，基于区间长度进行加权[9]。考虑因每列列车运行区间长度lf,s不同造成乘客感知体验差异，本文将各列列车在车人数qf,s,k再次加权得到权重为

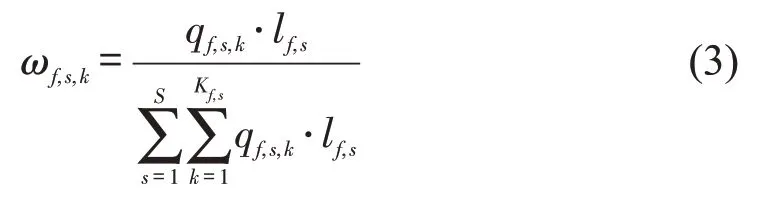
易知，线路负荷均值指标γf取值在0和规定的最大列车满载率之间。与线路列车平均满载率指标相比，负荷均值指标更加考虑乘客拥挤度的影响，加重了列车满载率较大样本点的权重。当线路上各列车车型、编组一致时，考虑加权的负荷均值指标总是不小于线路列车平均满载率指标。证明如下：

首先，将负荷均值指标和线路列车平均满载率分别简写为γ和γ′，即

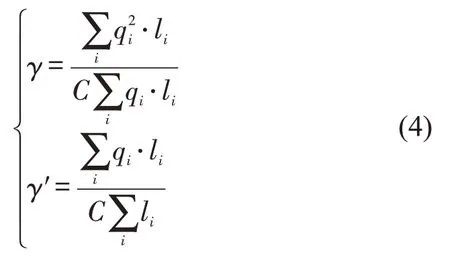
式中：qi、li分别为第i个样本在车人数、运行区间长度，C为列车定员。

由qi ＞0,li ＞0，根据柯西不等式可得

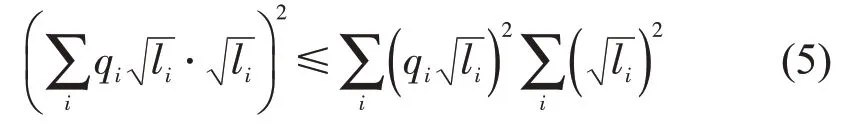
整理可得

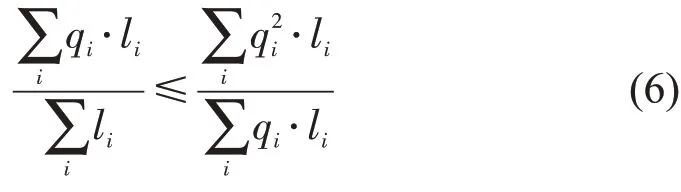
即γ≥γ′，证毕。

1.2 标准差率指标

标准差率为研究时段内，线路负荷分布偏差情况，体现均衡性，即

式中：E为期望值，表示所有样本的平均值。

从式(7)分析，标准差率指标受客流条件(q)、列车运载能力(C)及列车运行组织方案(K)影响，可表示为ψf(q,C,K)。标准差率越小，说明线路上所有列车运载能力利用在空间上越均衡，有利于企业开展运输组织工作；反之，说明越不均衡。当标准差率指标取值为0 时，表示所有列车负荷完全相等。另外，当乘客均匀到达且列车均匀发车时，线路所有区间同时增加或减小相同规模的运力，标准差率不变，即

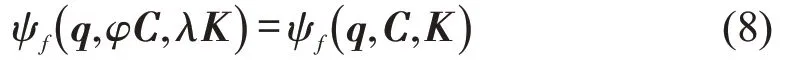
式中：参数φ、λ均为正数。从式(7)推导上这一结论是显然的。因此，只有相对提高大客流区间或大客流方向上的输送能力，才能够有效提高线路负荷的均衡性。

2 算例分析

2.1 算例参数

以某条衔接中心城区和城市外围的地铁线路为例展开算例分析。

(1)线路参数

算例线路总长61.8 km，设站30座，各区间长度如表1所示。

表1 算例线路区间长度Table 1 Section length of line

(2)客流条件

最大断面流量发生在上行方向第12 个区间，断面客流量为3.83 万人次·h-1。固定上行方向客流，通过改变下行方向客流规模，得到客流方向不均衡系数分别为1.0，1.1，1.2，…，2.0的11种客流类型，如图1所示。需要说明的是，根据方向不均衡系数计算公式[2]，2.0 为极限情况，即一个方向客流远小于另一方向。

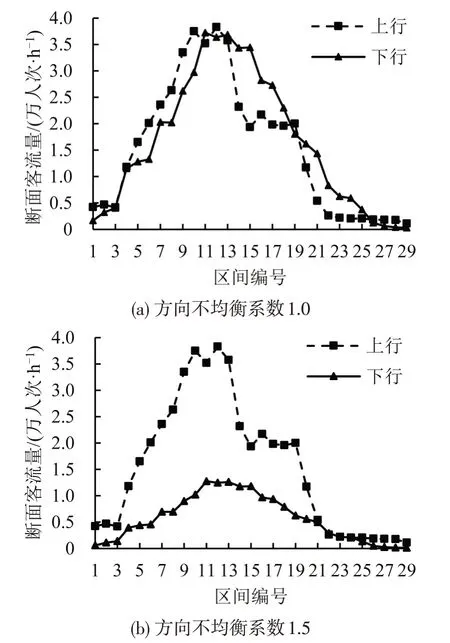
图1 算例客流的几种情形Fig.1 Several cases of passenger flow

(3)初始开行方案

初始开行方案按照单一交路、列车6A编组、双向均衡发车制定，取最大满载率约束为120%，单节车厢定员平均为310 人·节-1，发车频率为18 对·h-1

(满足最大满载率约束的最小发车频率)，此时最大断面列车满载率为114.4%。

2.2 负荷水平评估结果

(1)负荷均值指标

为分析考虑加权计算的负荷水平均值结果，将负荷均值指标同线路列车平均满载率指标进行对比，如图2和图3所示。

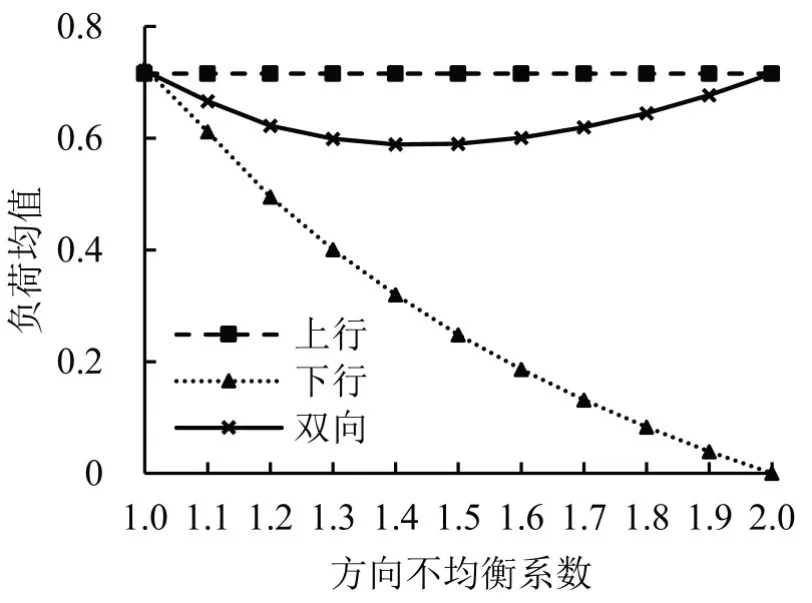
图2 负荷均值Fig.2 Weighted mean value of line loading

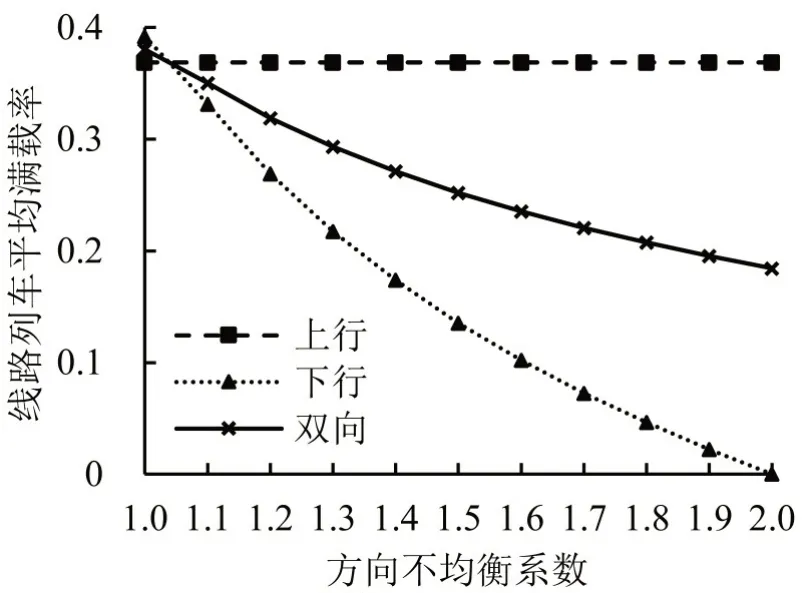
图3 线路列车平均满载率Fig.3 Line load factor

因加大了拥挤度更高的列车对负荷水平贡献的权重，考虑加权计算的负荷均值指标均大于线路列车平均满载率指标，这与模型分析结果相一致。单一方向的负荷均值与客流规模呈正相关，与线路列车满载率指标变化规律一致。比如，客流方向不均衡系数从1.0变化到1.1时，下行方向负荷均值从0.73 减小到0.61，线路列车满载率从0.39 减小到0.33，变化率分别为-15.7%和-15.4%。

从双向负荷均值指标看，当方向不均衡系数为1.4 时，双向负荷均值取到最小值0.59。这是因为当方向不均衡系数不超过1.4 时，随着下行方向客流减小，根据本文负荷均值计算方法，下行方向列车对线路负荷的贡献逐渐下降，使双向负荷均值减小；当方向不均衡系数大于1.4时，下行最大断面客流小于1.64万人，下行方向列车最大满载率将小于36.4%，上行仍为80.1%，双向列车负荷相差已经非常大，大客流方向计算样本的权重高，对线路负荷水平的贡献程度大，抵消了下行方向客流减小带来的影响。

可见，从负荷均值指标变化的角度，本文算例中方向不均衡系数大于1.4 时，在双向对称发车模式下线路双向负荷水平均值指标达到变化临界点，双向负荷不均衡达到较高程度，在小客流方向的列车运载能力利用虚弥，运输企业应考虑运力优化措施以提高能力利用的均衡效果。

(2)标准差率指标

标准差率指标计算结果如图4所示。可以看出，单一方向的标准差率指标不变，这是由于上行方向客流固定，下行方向各断面流量是按照等比例设置，各断面列车负荷同等程度变化，标准差率指标理论上不会变化。方向不均衡系数为1.9 时，下行方向标准差率出现小幅度减小是设置断面客流时保留整数精度所致；方向不均衡系数为2.0时，由于下行方向客流按理想设置为0，则式(7)中期望为0，导致无法计算标准差率指标。

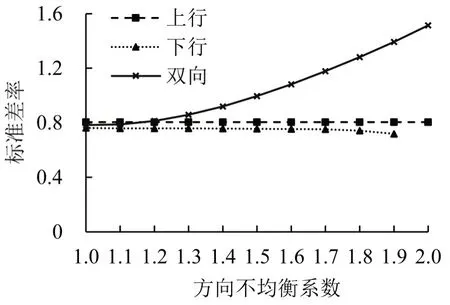
图4 标准差率Fig.4 Coefficient of variation of line loading

随着双向客流不均衡系数增加，考虑双向负荷的标准差率指标出现迅速增长。方向不均衡系数为1.0时，标准差率为0.78，主要体现的是各个断面列车负荷不均衡程度；当方向不均衡系数取极限2.0时，当前算例中标准差率指标增加到1.5。

根据模型分析结果，线路所有区间的运力同等规模变化不影响线路负荷的均衡性指标(标准差率)，故重点分析交路和不成对行车模式对负荷水平的影响。

2.3 列车交路的影响分析

以方向不均衡系数为1.0 时的客流为例分析。该客流条件下，上行方向断面客流不均衡系数为2.48，下行方向为2.26。文献[5]研究认为断面客流不均衡系数大于1.8 时，可以考虑开行大小交路。算例线路上行方向第9～13区间的断面客流量均超过3万人次·h-1，显著大于其他断面客流，应重点提高该区段的输送能力。假设各车站均具备折返作业条件，大、小交路列车发车频率各为12对·h-1，小交路列车折返站分别为s1 和s2，且s1 小于等于8，s2大于等于14，以覆盖9～13区间。

大、小交路模式下，列车折返位置影响乘客选择行为和列车满载率，文献[5]假设乘客均匀到达并乘坐第1趟直达列车来计算线路双向各区间列车在车人数，进而计算乘客总候车时间、列车走行公里及本文的负荷水平指标。为满足列车最大满载率不超过120%的约束，当s1分别设置在车站1～6时，要求s2分别不小于16、17、18、19、20、22；当s1为车站7和8时，方案不可行。得到s1小于等于6，s2大于等于16时负荷水平情况如图5和图6所示。

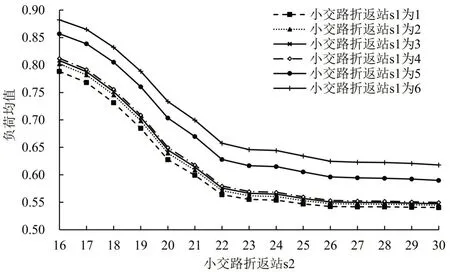
图5 大、小交路模式下负荷均值Fig.5 Weighted mean value of line loading under full-length and short-turn routing

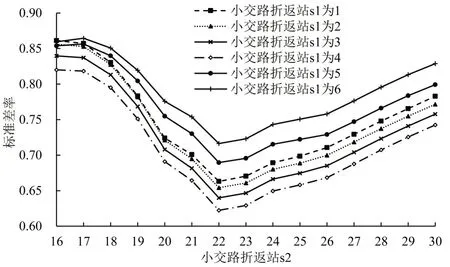
图6 大、小交路模式下标准差率Fig.6 Coefficient of variation of line loading under full-length and short-turn routing

可以看出，小交路折返位置对降低标准差率，提高线路负荷均衡性具有重要作用。单一交路模式下(即s1 为1,s2 为30)，标准差率为0.78，负荷均值为0.54。当s2 为22 时，标准差率取到最小值；s1为4时，标准差率下降到最小值0.62，并且与单一交路相比，负荷均值并未发生较大变化(为0.58)，线路列车平均满载率从27.7%提高到37.3%，如表2所示。这意味着在列车运载能力得到更充分利用条件下，乘客整体拥挤度水平保持稳定，并取得最佳负荷均衡效果；但是降低了非小交路区段乘客服务水平，有14.3%的乘客平均候车时间从2.5 min增加到5 min。

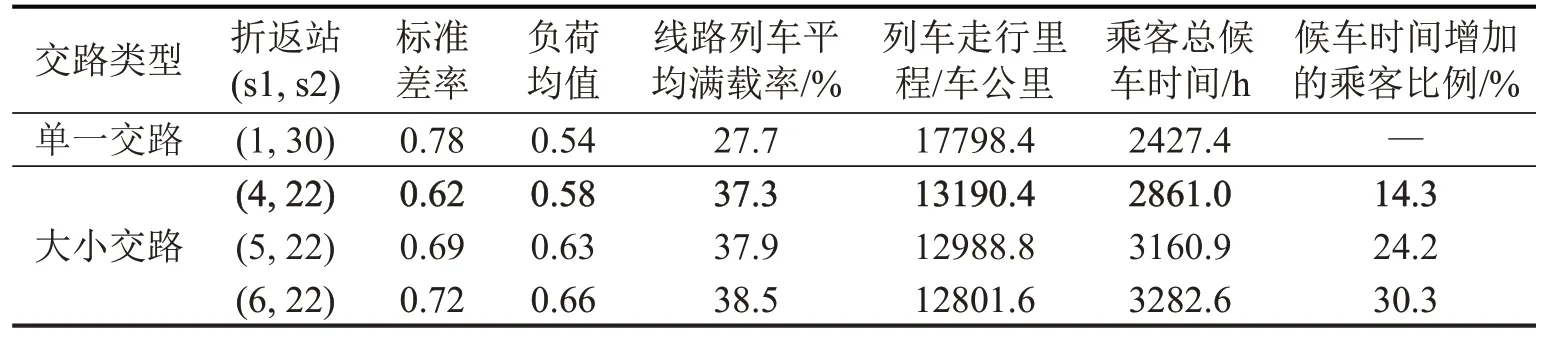
表2 不同交路方案计算结果Table 2 Results under different routing schemes

2.4 不成对行车模式的影响分析

总共控制48 个上线车次，初始为双向均衡发车，通过增加上行方向(大客流方向)车次，减少下行方向车次的方式设置不成对行车模式。考虑最小2 min、最大6 min 的发车间隔约束和最大满载率120%约束，假设乘客平均候车时间为发车间隔的0.5倍，计算得到乘客总候车时间指标如图7所示。

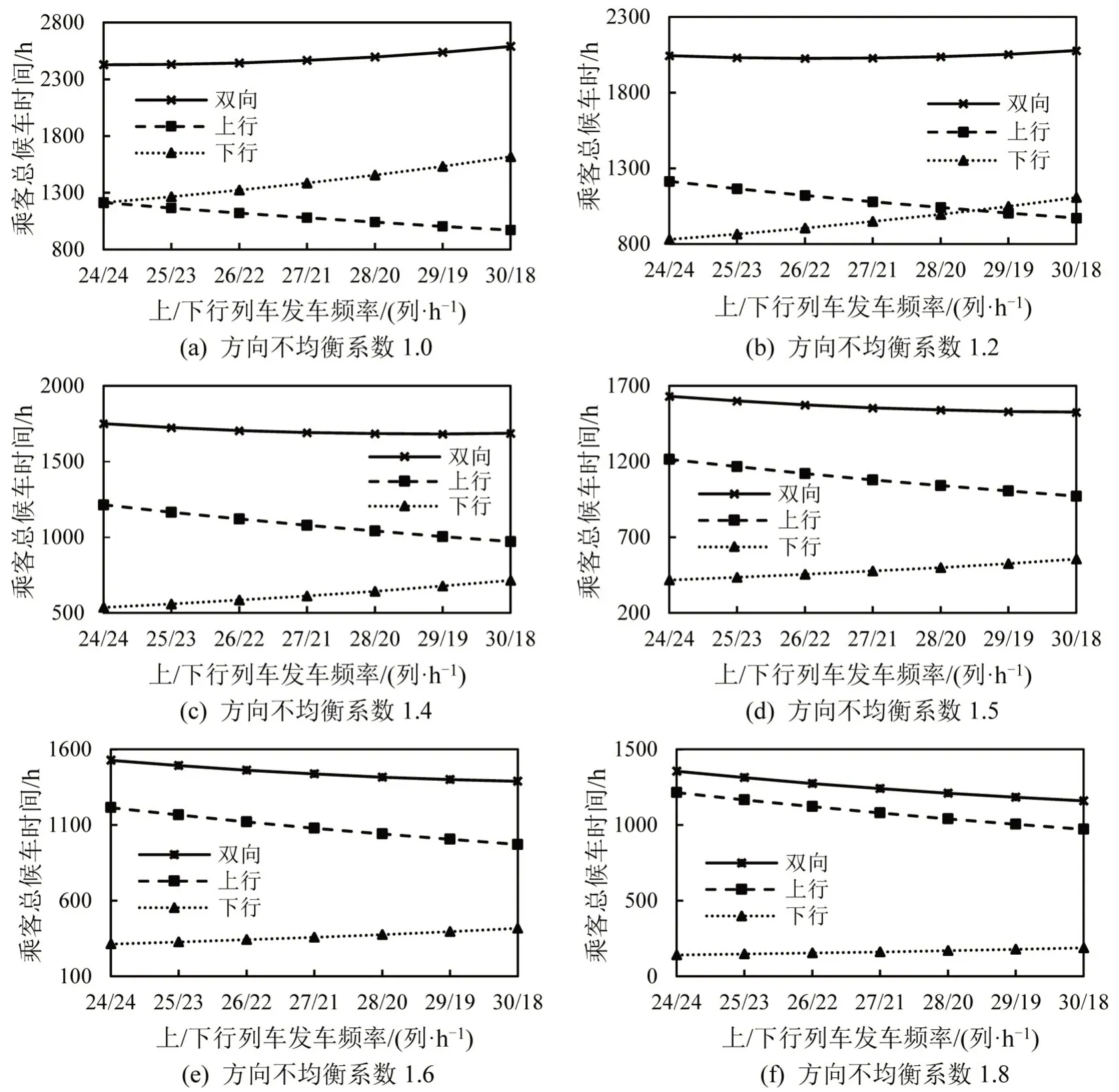
图7 不成对行车模式下乘客总候车时间Fig.7 Passenger waiting time under bidirectional uneven operating mode

可以看出，当方向不均衡系数不超过1.4时，双向乘客总候车时间随上行发车频率增加表现出增加或小幅下降的趋势；当方向不均衡系数大于1.4时，双向乘客总候车时间出现较明显下降。从这个角度看，不成对行车模式在客流显著不均衡时具有更大的优化空间。

以方向不均衡系数为1.5时的典型潮汐客流为例，分析不成对行车模式对负荷水平的影响，结果如图8和图9所示。

图8 不成对行车模式下负荷均值Fig.8 Weighted mean value of line loading under bidirectional uneven operating mode

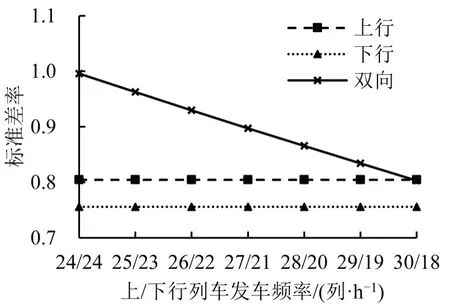
图9 不成对行车模式下标准差率Fig.9 Coefficient of variation of line loading under bidirectional uneven operating mode

双向对称发车(24 对·h-1)时，线路双向负荷均值和标准差率分别为0.44、1.00。不成对行车模式通过提高小客流方向负荷均值，降低大客流方向负荷均值，显著降低双向的标准差率。上行方向发车数每增加1列(同时下行方向减少1列)，双向标准差率平均减少0.03。上、下行发车频率为30 列·h-1、18 列·h-1时，标准差率从1.0 降低到0.8，优化了20.0%；乘客总候车时间从1631 h减少到1527 h，优化了6.4%。

但是不成对行车模式将增加车底周转难度，具体实施的可行性受到车辆段存车能力、可用车底数量、车底接续等约束，仍待研究。

3 结论

本文以列车负荷为评价单元，建立了表征线路负荷平均水平与偏差程度的二维评价指标，并设计算例研究了客流特征、列车运行组织方案等因素对线路负荷水平的影响效果。主要结论如下：基于本文的客流条件，在分析负荷加权均值指标时，发现客流方向不均衡系数超过1.4 时，在双向对称发车模式下线路负荷均值达到拐点，应考虑运力优化措施以提高能力利用率；在分析负荷标准差率指标时，在乘客均匀到达和均衡发车的前提下，线路所有区间的运力同等规模变化不影响线路负荷的均衡性；组织大、小交路与不成对行车可以改善线路负荷的均衡性效果，但是以降低部分乘客服务水平或增加车底周转难度为代价。后续研究可以在本文基础上展开不同线路类型的负荷水平特征评估，并进行有针对性的运输组织工作优化工作。