基于遗传算法优化粗糙决策模型的光伏电站发电量的影响因素研究

杨 旭，易 坤，杨 浪

(中国电建集团贵州工程有限公司，贵阳 550003)

0 引言

光伏发电是通过将照射到光伏组件上的太阳辐射转换为直流电来发电的方式。由于单块光伏组件转换的直流电的电压较低，所以需要将一定数量的光伏组件串联，形成高电压，然后通过逆变器转换为一定频率的正弦交流电注入到电网，进而为客户提供绿色清洁的电力。

随着全球光伏行业的竞争日益激烈，为了提高光伏电站的发电量，降低光伏电站的度电成本，对光伏电站的设计及设备的要求越来越高，光伏电站的设计必须从精细化、定制化出发。影响光伏电站发电量的因素众多，不同因素之间的相互影响及其交互影响极其复杂。由于每一项系统损失都将直接反映到光伏电站的发电量损失中，因此以往的研究大多是针对光伏电站单一的系统损失。

本文引入粗糙集，在粗糙决策模型的基础上，采用遗传算法对光伏电站发电量属性和属性值的约简进行了诊断，以此来寻找光伏电站发电量的主要影响因素。遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局的优化搜索算法，具有广泛适用性。本研究选取了8个参数作为条件属性，建立了光伏电站发电量的诊断模型，通过计算分析，得到了影响光伏电站发电量的决策规则，为寻找光伏电站发电量的主要影响因素提供了一种新的方法。

1 粗糙集的原理和遗传算法优化的粗糙集

1.1 粗糙集的基本原理

在模型设计过程中，由于存在较多的干扰因素，众多因素联合进行优化设计的过程复杂且计算量大。为此，需要对参数进行初步的筛选，以确定对输出结果影响较大的因素组合，然后在此基础上进行进一步的优化设计，从而可以大幅减小工作量。

粗糙集理论[1]是由波兰数学家PAWLKA于1982年提出的，该理论对于处理研究中的不确定性问题具有显著的优势，其能够在无任何数据预备或额外信息的情况下对数据进行处理，然后得到数据之间的潜在关系。粗糙集是一种处理模糊性和不确定性问题的新的数学方法，通过信息压缩、不确定信息的识别和评估来揭示数据之间的潜在规律性[2]。

与概率统计、证据理论、模糊集等数学方法相比，粗糙集与这些方法有一定的联系，但同时也具有不可替代的优势。在粗糙集处理过程中不需要对参数的概率分布进行求解，而概率统计需要获得概率分布才可以求解；粗糙集处理过程中不需要对参数的概率进行赋值，而证据理论[3]要求参数必须具有概率值；同时，粗糙集处理过程中也不需要获得隶属函数，而模糊集[4]则需要事先获得隶属函数。

粗糙集理论[5]是在保持信息库分类能力不变的前提下，可以导出问题的决策和分类规则的数学工具。在粗糙集理论中，知识用信息系统来表示，信息系统的属性进一步可分为条件属性和决策属性。属性约简是粗糙集理论中的重要问题，其是在保持分类能力不变的前提下，删除冗余信息的过程，最终将决策表中的知识简化成少量的决策规则。

1.2 粗糙集的基本概念

粗糙集理论的基本概念主要包括信息系统的属性、决策属性关于条件属性的正域、决策属性对于条件属性的依赖度3个方面。

1)信息系统的属性。设信息系统S为[6]：

式中，U为全体样本集(论域)，U={x1,x2,…,xn}，n为样本集的个数；A为全体属性集，A=C∪D，其中，C为条件属性子集，D为决策属性子集，C∪D=φ；V为全部属性的值域；设a是任意一个属性，a∈A，xi是任意一个对象，xi∈U，i=1, 2,…,n，则f(xi,a)表示xi在a属性的取值，f(xi,a)∈Va。

2)决策属性关于条件属性的正域。决策属性d关于条件属性c的正域posc(d)可表述为：

3)决策属性对于条件属性的依赖度。决策属性d对于条件属性c的依赖度rc(d)可表述为[7]：

1.3 基于遗传算法优化后的粗糙集算法

本文介绍的粗糙集理论算法主要包括连续属性离散化法和遗传算法属性约简。

1.3.1 连续属性离散化法

所有的参数变化区域是连续的，粗糙集处理数据需要设立若干个阈值，将连续的区域划分为离散区间；然后在此基础上，使用不同符号或数值进行命名或替代。在此过程中会将输入的条件属性划分成有限的区域，每个区域中的决策值一致。例如，条件属性空间为1～M，对每个条件属性进行离散，离散区分为1、2或1、2、3等。

1.3.2 遗传算法属性约简

属性约简问题属于多项式复杂程度的非确定性(NP-hard)问题，肖厚国等[8]提出了基于遗传算法约简冗余条件属性得到简化决策表的具体算法。NP-hard问题中最繁杂的问题是属性的组合爆炸问题，一般需要采用启发式算法来解决该问题，这也是引入遗传算法的原因。遗传算法属性约简主要涉及到染色体编码、适应度函数和遗传算子的确定。

1)染色体编码。根据条件属性的个数，对每个个体进行编码。由于遗传算法不能直接处理条件属性数据，因此必须通过编码将数据表示成遗传空间的基因型的串结构数据；编码使用固定长度的二进制字符串表示群体中的个体，其等位基因是由二值符号{0,1}组成。二进制字符串的长度等于条件属性的个数，个体与编码一一对应。例如“11110000”表示1个个体，该染色体长度为8，其中每一位对应1个条件属性；若取值为“1”，表示选择其对应的条件属性；若取值为“0”，则表示不选择其对应的条件属性。

2)适应度函数。通过适应度函数来控制算法的进化方向，保证进化向着最小约简进行。

适应度函数F(s)可以表示为：

式中，ls为染色体s中基因为1的个数；l为条件属性的个数。

3)遗传算子的确定。选择算子采用轮盘赌策略，变异算子采用均匀变异算子，交叉算子采用单点交叉算子；当迭代步数达到最大或reduct(C)=rc(d)时终止。

2 光伏电站发电量的诊断流程

本研究基于遗传算法对粗糙决策模型进行优化，建立了光伏电站发电量诊断模型，该模型的流程图如图1所示。

图 1 光伏电站发电量诊断模型的流程图Fig. 1 Flow chart of diagnosis model of power generation of PV power station

光伏电站发电量诊断的主要步骤为：

1)确定条件属性和决策属性。根据研究对象确认以光伏电站发电量作为决策属性；以光伏组件安装倾角、光伏阵列间距、光伏组件串联数、光伏组件和逆变器容配比、热交换系数、直流线损、交流线损、光致衰减(light induced degradation，LID)这8个参数作为条件属性。

2)连续属性离散化。该步骤是采用各种方法将连续的区间划分为小的区间，并将这些小区间与离散的值关联起来。常见的方法包括等宽法、等频法、基于聚类分析的方法等。本研究采用等宽法对条件属性和决策属性进行离散化，根据数值将条件属性和决策属性分别划分为大、小2个部分，并用不同代码表示。

3)根据决策表计算决策属性关于条件属性的依赖度rc(d)。

4)令reduct(C)=φ，逐个去掉条件属性，任意条件属性ci∈C，并重新计算决策属性关于剩余条件属性的依赖度，若此时得到的依赖度与完整属性依赖度一致，则终止计算；若不一致，则进入第5)步。

5)随机产生长度为l的二进制字符串作为初始种群，并按前文介绍的基本算法来计算初始种群每个个体的适应度。

6)按轮盘赌策略选择个体，交叉概率为PC，变异概率为PM，得到新一代种群中每个个体的适应度。

7)判断是否达到最大迭代次数或连续t代不进化(设置的收敛标准)。若结论为“是”，则终止计算；若结论为“否”，则返回第6)步，直到结论为“是”为止。

3 光伏电站发电量诊断的示例分析

本文以乌克兰某148 MW光伏电站为例对建立的光伏电站发电量诊断模型进行应用分析。该光伏电站的参数取值主要为：光伏组件的安装倾角为15°～35°，光伏阵列的间距为5～15 m，光伏组件串联数为15～29块，光伏组件和逆变器容配比为1:1～1.5:1，热交换系数为15～29 W/(m2•K)，直流线损为0.8%～2.2%，交流线损为0.5%～1.2%，LID为1%～3%。该光伏电站每kWp装机容量的年发电量为1095～1265 kWh。

3.1 决策表的建立

按光伏电站发电量诊断主要步骤中的第2)步对该光伏电站的条件属性和决策属性进行离散处理。其中，选择的条件属性的8个参数分别为光伏组件安装倾角(c1)、光伏阵列间距(c2)、光伏组件串联数(c3)、光伏组件和逆变器容配比(c4)、热交换系数(c5)、直流线损(c6)、交流线损(c7)、LID(c8)。以平均值为界，条件属性按数值大小分为大、小2个区域，分别用代码“0”和“1”表示；决策属性按数值大小均分为小、大2个部分，分别用代码“2”和“3”表示。从所有组合中随机抽取12组数据，离散处理后的光伏电站发电量的决策规则如表1所示。

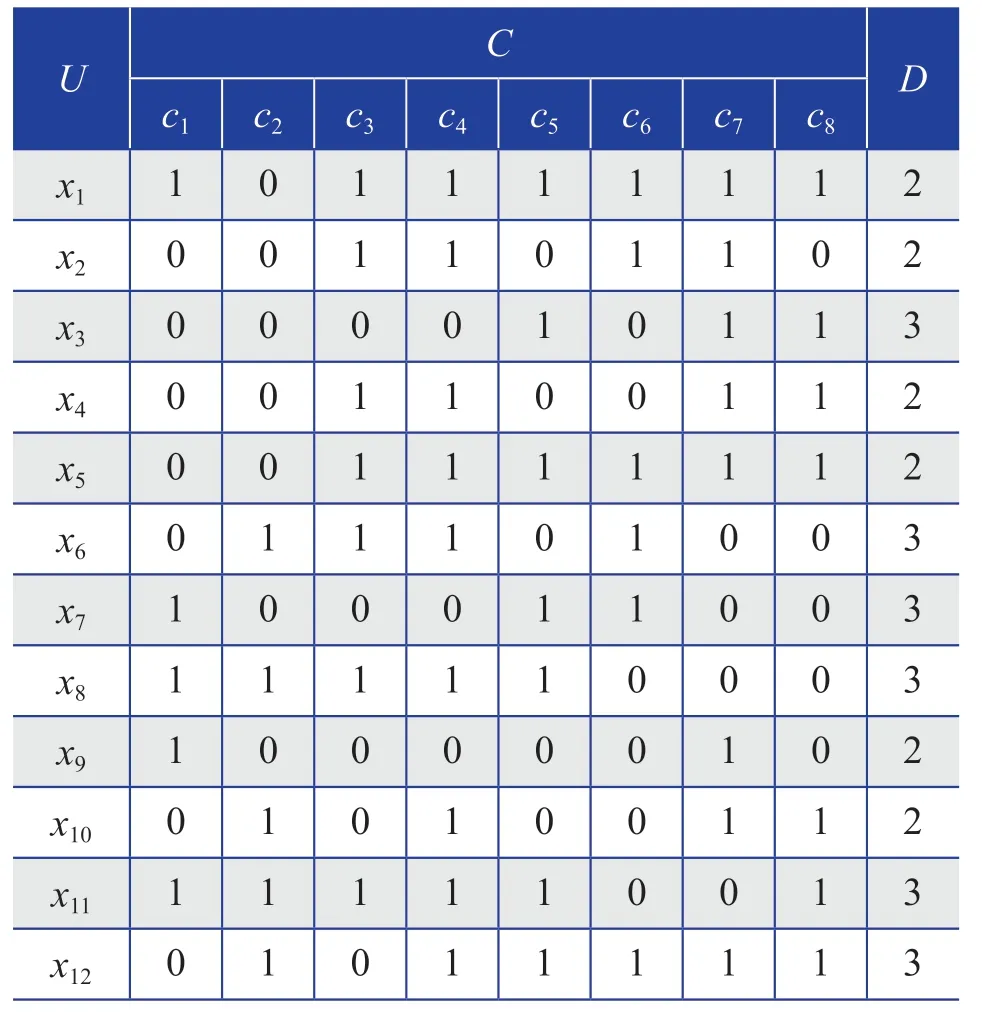
表1 离散处理后的光伏电站发电量的决策规则Table 1 Decision rules of power generation of PV power station after discrete processing

3.2 条件属性约简

选取PC=0.7、PM=0.01、最大代数为150，得到最优解为00101010，即条件属性c3、c5、c7保留。因此，可得到条件属性约简后的光伏电站发电量的决策规则，如表2所示。

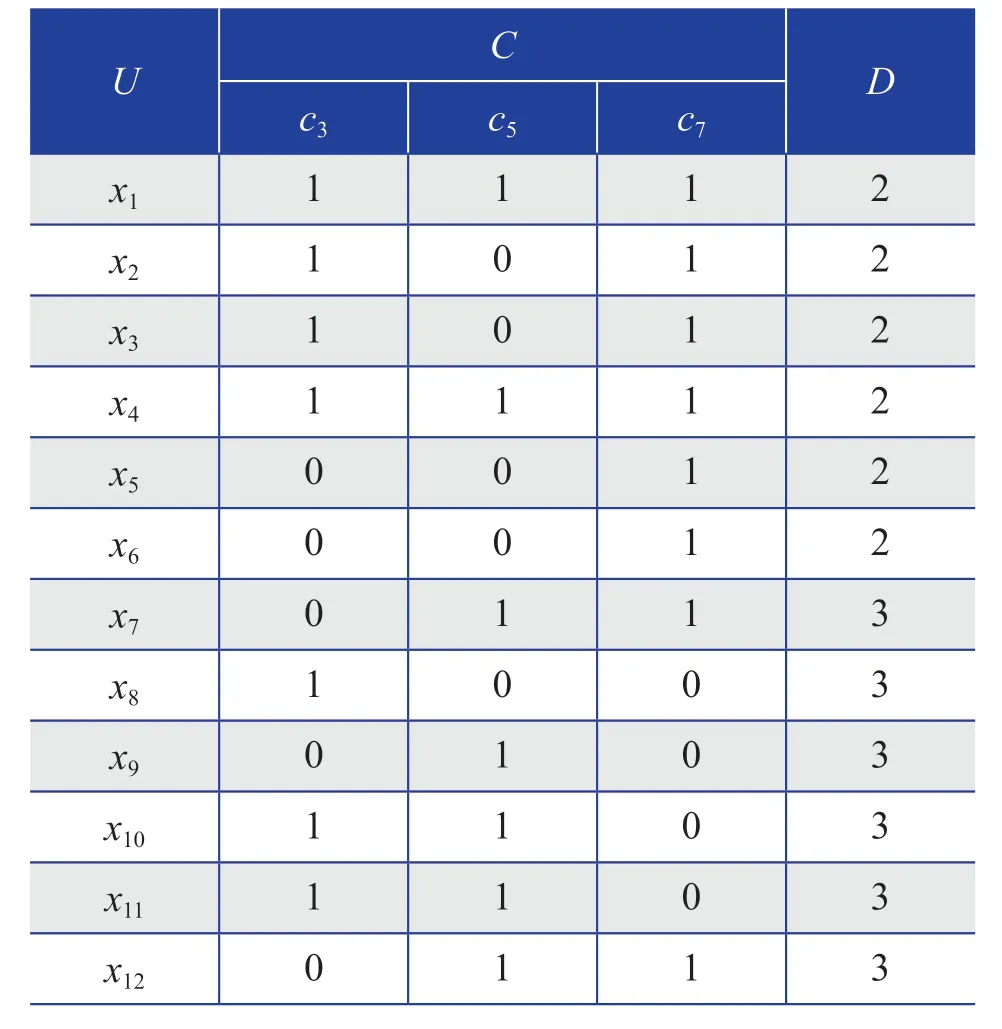
表2 条件属性约简后的光伏电站发电量的决策规则Table 2 Decision rules of power generation of PV power station after conditional attribute reduction

3.3 决策规则

根据条件属性约简后的决策规则结果，去掉冗余和重复属性后，得到最终的光伏电站发电量的决策规则如表3所示。

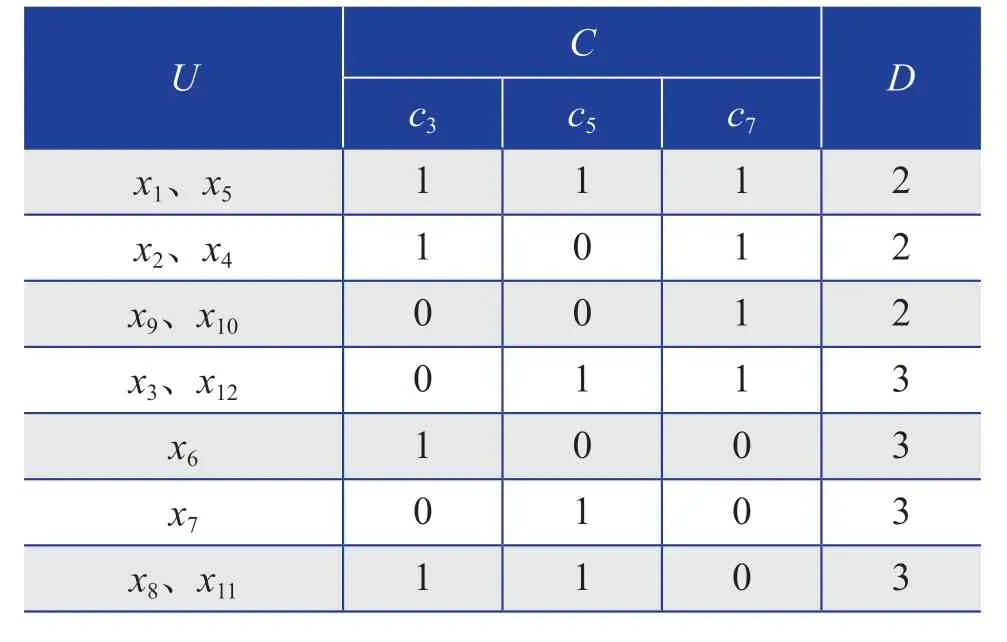
表3 最终的光伏电站发电量的决策规则Table 3 Final decision rules of power generation of PV power station

从表3中可以看出，在所研究的影响因素中，对光伏电站发电量影响最大的是光伏组件串联数、热交换系数及交流线损这3个因素。这3个因素的关系主要为：

1)当光伏组件串联数、热交换系数及交流线损这3个影响因素均较大时，光伏电站的发电量较低；

2)当光伏组件串联数、交流线损较大，而热交换系数较小时，光伏电站的发电量较低；

3)当光伏组件串联数、热交换系数均较小，而交流线损较大时，光伏电站的发电量均较低；

4)当光伏组件串联数较小，而热交换系数和交流线损较大时，光伏电站的发电量均较高；

5)当热交换系数较大且交流线损较小时，无论光伏组件串联数如何，光伏电站的发电量均较高；

6)当光伏组件串联数及热交换系数较大，而交流线损较小时，光伏电站的发电量较高。

由于实际运行中的大型地面光伏电站的热交换系数均较大，因此上述决策表可以进行进一步地约简，即去掉热交换系数c5。进一步约简后发现，若要保证光伏电站的发电量较高，则需保证交流线损较小，或交流线损较大时光伏组件串联数不宜过大。

4 结论

本文在粗糙决策模型的基础上，引入遗传算法来寻找光伏电站发电量的主要影响因素。以光伏电站发电量作为决策属性、选取了8个参数作为条件属性，建立了光伏电站发电量的诊断模型，并通过计算分析，最终得到了影响光伏电站发电量的决策规则。研究结果表明：

1)在本研究中光伏电站所处的地区，所有光伏电站发电量的影响因素中，光伏组件串联数、热交换系数及交流线损这3个影响因素对光伏电站的发电量情况起到了决定性作用。

2)对热交换系数较大的大型地面光伏电站而言，降低交流线损，或在交流线损较大时选择较小的光伏组件串联数对提高光伏电站的发电量有益。