铝合金带筋构件超声辅助旋压仿真研究
李晓凯,赵亦希,于忠奇,朱宝行,崔峻辉
(上海交通大学 上海市复杂薄板结构数字化制造重点实验室, 上海 200240)
流动旋压有利于实现带筋构件整体成形,据报道[1],旋压成形航天飞机燃料储箱带筋构件,可将材料切削量从90%降低至5%,大大降低成本,并且减少焊缝缺陷,提升可靠性,因此受到学界广泛关注.但是当构件相邻内筋之间的间距变大时,构件上材料流动差异显著,受到结构与芯模摩擦阻力等条件的约束,材料向筋部流动困难,容易出现内筋填充不足的问题,因此需要寻找改善的方法.
文献[2-5]表明,在切削、墩挤、旋压等工艺当中施加超声振动辅助,利用超声振动的声软化效应和减摩擦效应,对降低成形载荷有显著效果,并且能够降低成形件和工具之间的摩擦系数,提高成形工件的表面质量.而且超声振动对变形区温度不会有明显的影响[6-7],相较于热、电辅助成形,不会破坏铝合金材料的预先固溶效果,从而保证了构件的成形精度和力学性能.超声振动辅助旋压可以改善内筋填充的问题.
为进一步探讨在超声振动与旋轮力场的共同作用对内筋增高的效果,本文通过超声振动辅助单向拉伸试验研究了超声振动振幅对2219-O铝合金材料力学性能的影响.将声软化模型与传统硬化方程结合,建立了考虑声软化效应的2219-O铝合金硬化方程.分析振幅对表面粗糙度的影响规律,以反映减摩擦效应的程度.基于Abaqus平台建立了超声振动辅助旋压有限元仿真模型,获得了超声振动对带筋构件旋压过程中材料变形抗力、流动状况及筋填充高度的影响规律.
1 超声振动辅助单向拉伸试验
1.1 试验系统
试验材料选择2219-O铝合金棒状试样,可与超声振动变幅杆通过螺纹连接.试样尺寸设计参照GB/T 228.1-2010标准[8],如图1所示.试样直径d=5 mm,标距l0=25 mm,总长l=66 mm,夹持端带有M12螺纹,变形区与夹持端过渡圆角半径r=5 mm.

图1 单向拉伸试样(mm)Fig.1 Uniaxial tensile specimen (mm)
在5t-SUNS电子万能实验机上搭建超声振动辅助单向拉伸试验系统,如图2所示,主要包括超声振动系统、拉伸试验机与测量系统.超声振动装置主要包括超声波发生器、换能器、变幅杆.采用鸿劲HJ20-3500超声波发生器,通电产生高频交流电信号.通常情况下,发生器频率越高时,最大输出功率越小,因此选用频率为20 kHz,最大输出功率可达 3 500 W.换能器利用压电陶瓷的压电效应,将电信号转化为机械振动.变幅杆采用阶梯状结构,起到放大振幅的作用.装置可通过改变输出功率的大小控制振幅.变幅杆末端与试样通过螺纹连接,带动试样振动.在变幅杆节点位置安装固定法兰,通过法兰将超声振动装置固定在机架上.

图2 超声振动辅助单向拉伸试验系统Fig.2 Uniaxial tensile test system assisted with ultrasonic vibration
为避免超声振动导致接触面摩擦力不足而使试样脱落,设计图2中所示的工具头,工具头下端为圆柱状,攻有螺纹,可与试样连接,上端圆角过渡为板状,被夹具夹持.一方面,振动传递到工具头会发生衰减,从而降低减摩擦作用,另一方面,工具头增大了与夹具间的接触面积,使试样固定牢靠.
1.2 试验方案
试验中,试样与变幅杆通过螺纹连接,存在装配间隙,若拉伸机与超声振动同时开启,高频振动将使两者相互撞击产生刺耳噪音,随着拉伸过程进行,噪音会逐渐加强,可能会导致试样提前失效.文献[9]指出,超声振动对材料在弹性阶段的特性无影响,只会改变材料的塑性性质.因此本试验采取步骤为:先开启拉伸机,材料产生弹性变形,尚未进入塑性变形时加入振动,此时试样受到的拉力使得螺纹之间紧密配合,可以避免撞击现象,同时材料的塑性变形阶段不受影响.

图3 无超声振动辅助单向拉伸力-位移曲线Fig.3 Force-displacement curve of uniaxial tensile test without ultrasonic vibration
首先确定2219-O铝合金的弹性变形范围,图3为无超声振动辅助单向拉伸试验得到的力-位移曲线,图中:F为拉伸力,x为位移.可以看出,F<1 200 N时,为弹性变形阶段.试验过程中,当F=1 000 N时,开启超声振动.设置拉伸速率为1.5 mm/min,设置超声振动振幅ζ=0, 3, 6, 9 μm.由试验机获取力随时间变化的曲线,通过数字图像相关测量系统(DIC)设备获取应变随时间变化的曲线.
1.3 试验结果
图4为2219-O铝合金在不同超声振动振幅条件下的单向拉伸工程应力(σe)-应变(εe)曲线.可以看出,随着振幅的增大,材料的应力曲线明显降低,说明超声振动能够有效降低材料的变形抗力.

图4 不同振幅下单向拉伸工程应力应变曲线Fig.4 Engineering stress-engineering strain curves of uniaxial tensile test at different amplitudes
从应力应变曲线中测得材料力学参数随振幅的变化如表1所示.可以看出,随着振幅的增大,虽然延伸率δ有所减小,但屈服强度σs和抗拉强度σb逐渐下降,当振幅达到9 μm时.屈服强度降低达到67.6%,说明超声振动能够有效促进材料屈服,降低成形载荷.
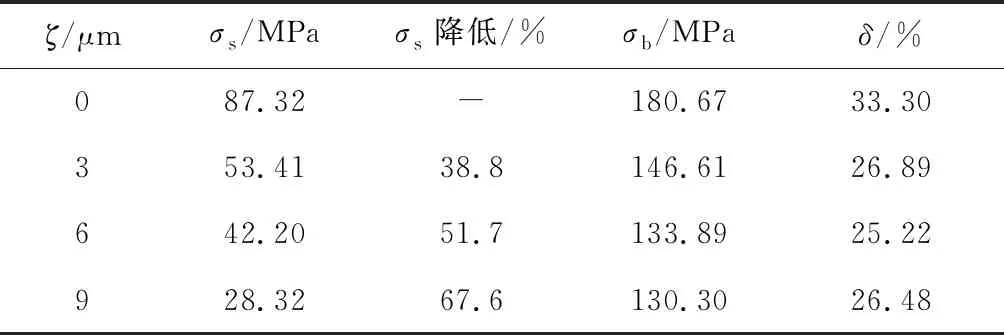
表1 不同振幅下2219-O铝合金力学性能
1.4 考虑声软化效应的2219-O铝合金硬化方程
1.4.1硬化方程建立 许多学者曾对声软化效应进行了定量研究,Siddiq等[10]通过研究认为声软化引起的应力下降正比于振幅的平方,而Huang等[11]用同样的试验方法研究铜发现声软化引起的应力下降正比于振幅.姚喆赫[12]在9.3 kHz的振动频率下,设置输入电压为0~60 V进行纯铝的墩锻试验.认为位错受超声振动激活越过障碍的过程与热激活过程类似,因此基于包含热激活模型与位错动力学模型的晶体塑性理论框架建立了声软化理论模型.这些研究普遍专注于声软化效应引起的应力减小量,并没有考虑材料本身的加工硬化,而且对于不同的材料,所得到的规律相差较大.本研究将姚喆赫的声软化理论与传统的材料硬化模型进行结合,基于试验结果识别2219-O铝合金材料参数,得到2219-O铝合金考虑声软化效应的硬化方程.
流动应力的减小量与超声能量密度的关系为
(1)
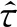
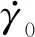
(4)
式中:C为与材料特性有关的参数.令λ=Δσ/σ,其中Δσ=σ-σultra,为施加超声振动后的应力减小量.由此得到考虑声软化效应的材料硬化方程:
σultra=σ-β(EC)mσ1-m
(5)
σ由传统的材料硬化方程表示,描述材料的加工硬化行为.E通过计算得出;β、C及m通过超声振动辅助试验数据拟合得到,体现声软化作用.文献[12]的试验结果认为,对于纯铝材料,声软化作用仅由E决定,但是对于本研究中的2219-O铝合金,相关参数仍需要根据试验结果判定.
1.4.2参数确定 无超声振动辅助时2219-O铝合金的硬化曲线可由Swift方程σp=K(ε0+εp)n拟合得到,如图5所示,图中:σp为塑性应力;εp为塑性应变,方程参数K=334.47 MPa,ε0=0.000 89,n=0.21,即
σp=334.47(0.000 89+εp)0.21
(6)

图5 无超声振动时材料硬化方程拟合Fig.5 Hardening equation fitting of material without ultrasonic vibration
将式(6)代入式(5),并且将超声振动振幅为3、6、9 μm 时得到的塑性应力应变曲线进行拟合,拟合结果如图6所示,得到不同振幅下β、C及m的数值,如表2所示.与纯铝材料不同的是,2219-O铝合金在超声振动辅助成形时,β、C随振幅的增大而减小,进一步拟合β、C与振幅的关系(图7)可以发现,EC与振幅有明显的线性关系,β与超声振幅存在指数关系,并且可以通过式(7)与(8)表达.m与振幅之间没有明显的关系,通过取平均值确定m=0.77.
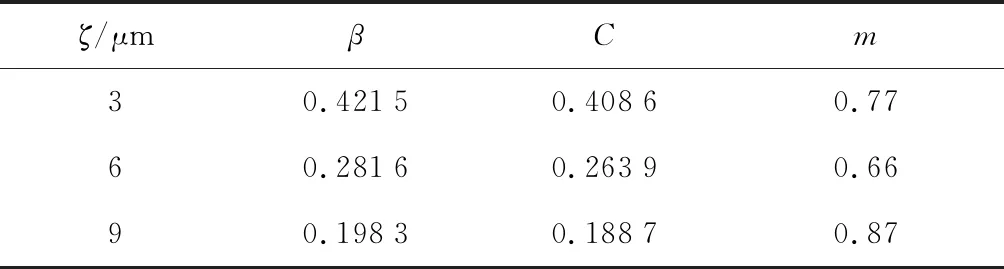
表2 不同振幅下的材料参数Tab.2 Material parameters at different amplitudes

图6 声软化效应有关参数拟合曲线Fig.6 Fitting curve of parameters of acoustic softening effect

图7 参数β、EC与ζ的关系Fig.7 β,EC versus ζ
β=2.859ζ-0.587
(7)
EC=-16.71+3.09ζ
(8)
联立以上结果得到考虑声软化效应的2219-O铝合金硬化方程为
σt=334.47(0.000 89+ε′)0.21
-2.859ζ-0.587(-16.71+3.09ζ)0.77
[334.47(0.000 89+ε′)0.21]0.23
(9)
1.4.3方程验证 为验证所得方程的准确性,将振幅设置为12 μm再次进行一组试验,在式(9)中代入ζ=12 μm,与试验结果进行比较,如图8所示.可以看出,试验结果与理论预测结果吻合较好,说明本文建立的材料方程能够较准确地描述2219-O铝合金在超声振动辅助条件下声软化与加工硬化结合的规律,保证仿真结果的可靠性.

图8 考虑声软化效应的硬化方程验证Fig.8 Verification of hardening equation considering acoustic softening effect

图9 超声振动辅助压缩试验系统Fig.9 Compression test system assisted with ultrasonic vibration
2 超声振动辅助压缩试验
为研究超声振动的减摩擦效应,进行超声振动辅助压缩试验,通过试样表面粗糙度的变化规律推算减摩擦效应的程度.带筋构件旋压过程中筋部材料的成形受到与芯模间摩擦力的影响,且摩擦力的方向与材料所受压应力方向垂直.为研究超声振动的减摩擦效应,进行超声振动辅助压缩试验来模拟实际工况,通过试样表面粗糙度的变化规律推算减摩擦效应的程度.
试样设计参照GB/T 7314-2005标准[13],选用侧向无约束圆柱试样,直径d=5 mm,高度L=1.2d,试验装置如图9所示,在变幅杆末端连接直径为12 mm的压头,试样的上表面与压缩方向垂直.试验方案与单向拉伸试验类似,首先加载至 1 000 N,然后施加超声振动,保持相对压缩率一定,仅改变振幅为0、3、6、9 μm.使用扫描电子显微镜观察压缩后试样表面形貌,使用表面粗糙度测量仪 SJ-210 测量表面粗糙度,仪器分辨率为 0.001 6~0.025 6 μm.
图10所示为在不同振幅下压缩后试样的表面形貌.可以看出,施加超声振动后,试样表面光洁度明显提高,表面质量明显改善.
图11所示为不同振幅下试样表面粗糙度Ra.可以看出,随着振幅的增大,试样表面粗糙度逐渐减小,并且表面粗糙度与振幅存在近似线性的关系.线性拟合表面粗糙度与振幅的关系可得:
Ra=Ra0-0.024ζ
(10)
式中:Ra0为未施加超声振动时试样的表面粗糙度.
3 带筋构件旋压成形有限元建模分析
带筋构件材料在变形过程中的应力变化及流动行为不便从试验获得,需要借助有限元仿真进行研究.仿真模型基于试验原理建立,本研究提出的试验系统原理如图12所示,超声变幅杆带动旋轮产生超声振动,并沿构件径向加载,通过旋轮与材料的接触将超声振动作用于材料变形区.
本章基于Abaqus平台建立带筋构件旋压有限元模型,将前文所得超声振动的声软化与减摩擦规律加以应用, 进一步探讨在超声振动与旋轮力场的共同作用下对成筋过程的影响.

图12 带筋构件超声振动辅助旋压原理图Fig.12 Schematic of ribbed member auxiliary spinning assisted with ultrasonic vibration
3.1 带筋构件旋压有限元建模
首先建立无超声振动辅助带筋构件旋压有限元仿真模型,如图13所示,主要部件包括筒坯、芯模、旋轮等.筒坯为等壁厚圆筒形结构,芯模包括6条纵向筋槽与两条横向筋槽,纵横筋对材料的填充要求不同.本研究首先关注纵向筋的填充行为.部件的几何尺寸及仿真工艺参数如表3所示,其中进给速率相比于实际值适当放大,以提高仿真效率.

图13 带筋构件旋压有限元仿真模型Fig.13 Finite element simulation model of ribbed member spinning

表3 带筋构件旋压有限元仿真参数Tab.3 Finite element simulation parameters of ribbed member spinning
仿真所得结果如图14所示,选取图中划线位置测量纵向内筋高度,平均高度为0.67 mm.

图14 仿真结果与测量内筋高度位置Fig.14 Simulation results and measuring positions of height of ribs
3.2 带筋构件超声振动辅助旋压有限元建模
3.2.1模型建立 为了在仿真中体现超声振动的作用,在上述带筋构件旋压成形仿真模型的基础上,首先在式(9)中代入不同振幅,得到不同振幅下2219-O铝合金的塑性应力应变关系,以离散数值化的方式修正仿真模型中材料的塑性性质,体现不同振幅的声软化效应.在考虑超声振动的减摩擦效应时,由于摩擦因数与表面粗糙度为正相关的关系,且在本试验中表面粗糙度的变化范围较小,在试验范围内可近似认为摩擦因数与粗糙度为线性相关关系,因此通过式(10)可得到摩擦因数μ随振幅的变化关系,
(11)
式中:μ0为无超声振动辅助时的摩擦因数.相应地修正仿真模型中构件与芯模间的摩擦因数.通过以上两点修正建立起2219-O铝合金带筋构件超声振动辅助旋压有限元仿真模型.
3.2.2结果讨论 选取与图14所示相同位置进行测量,比较不同振幅下的内筋高度H,结果如图15所示.可以看出,随着振幅的增大,内筋高度逐渐升高,当振幅达到12 μm时,内筋高度可提高大约 1/3.
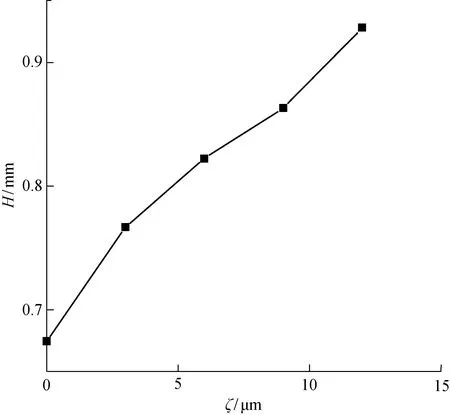
图15 不同振幅下的筋填充高度Fig.15 Height of ribs at different amplitudes

图16 不同振幅下筋部材料应力变化Fig.16 Stress changes of rib materials at different amplitudes
为进一步研究超声振动对筋部材料变形行为的影响,分析筋填充高度增加的机理.首先选取筋部单元输出其等效应力σm随时间变化的曲线,如图16所示.可以看出,随着超声振幅的增大,材料成形过程中的等效应力逐渐降低,说明超声振动能够有效降低材料的变形抗力,有利于材料成形.
在圆柱坐标系中,比较筋部单元有无超声振动时3个方向的位移,结果如图17所示.可以看出,施加超声振动后,材料切向的位移基本不变,轴向伸长的位移有所减小,径向向内的位移显著增大.
通过以上分析可见,超声振动能够有效减小带筋构件旋压成形时筋部材料的变形抗力,有利于材料变形,并且能够限制筋部材料在轴向的流动,有效促进材料径向的流动,与内筋成形时材料沿径向向内填充方向一致,因此提高了内筋高度.
3.2.3模型验证 为验证所建立仿真模型的准确性,在Okay800卧式旋压机上进行现场工艺试验,试验设备如图18所示,进给速率为0.5 mm/s,其他参数均与仿真模型相同,通过振幅为0、3、6 μm的试验结果对仿真结果进行验证,所得带筋构件如图19所示.测量实际所得零件纵向内筋高度分别为0.65、0.80、0.91 mm,仿真结果的平均误差约为6%,因此可以认为所建的带筋构件超声振动辅助旋压有限元仿真模型可以较为准确地模拟实际工艺过程,仿真结果可靠.

图18 带筋构件旋压试验设备Fig.18 Test devices of ribbed member spinning
4 结论
本文提出带筋构件超声辅助旋压方法,设计搭建超声振动辅助单向拉伸与压缩试验系统,获得超声振动的声软化与减摩擦规律,并通过仿真试验结合,得到超声振动对带筋构件旋压筋部成形过程的影响规律.
(1) 建立了超声振动辅助单向拉伸试验系统,基于单向拉伸试验结果,将声软化理论与传统硬化方程结合,建立了考虑声软化效应的2219-O铝合金硬化方程,同时体现材料的加工硬化与声软化行为,并且通过试验验证了方程的准确性.
(2) 超声振动对2219-O铝合金具有减摩擦效应,随着振幅的增大,试样表面粗糙度逐渐减小,并且存在近似线性的关系.
(3) 建立了带筋构件超声辅助旋压仿真模型,能够体现超声振动不同振幅下的声软化效应与减摩擦效应,并且通过试验验证了仿真模型的准确性.仿真结果表明,随着振幅的增大,材料的变形抗力逐渐减小,并且超声振动能够限制材料的轴向流动,促进材料向径向填充,最终可提高带筋构件的筋填充高度,当振幅达到12 μm时,内筋高度可提高约1/3.

