思维可视化，助力学生数学思维的生长

宋雪珠 唐诗颖 王彬

重庆市融汇沙坪坝小学  400038    重庆市凤鸣山中学  400037

[摘  要] 数学思维是数学学习力的核心部分，培养数学思维是发展数学核心素养的关键。通过对教材的二次开发、精准问题的设置、深度对话的发生和多元表征的运用，找到思考的切入点，让思维落到关键处. 在教学过程中，充分调动学生的多重感官、动手画图和操作、动口表达和对话等，让思维直观化、形象化、外显化，促进数学思维的发展。

[关键词] 思维可视化;画图;操作;表达;对话

数学思维是以数量关系和空间形式为思维对象，以数学的语言和符号为思维的载体，并以认识和发展数学规律为目的的一种思维 [1]。这样的数学思维具有高度的抽象性、内隐性，不利于教师培养学生的数学思维。如何在教学过程中让学生的思维外显，让教师把握学生思维路径、学习同伴之间相互理解多样化的数学思维进而掌握数学知识的本质？在教学中我们首先要思考如何让学生真正发生思维，再思考用什么手段让思维可视化。

■一、思维可视化的前提——思维真正发生

要想思维可视化，必须要发生真正的思维活动。数学是对数量关系和空间形式进行研究的一门科学，其概念、定理等都是基于现象的研究，通过归纳、概括、抽象出其本质，形成结论，具有高度的抽象化和理想化。枯燥的数学文本并不能很好地激发学生的思维，在教学中根据学生已有的生活和知识经验，教师通过创设情境、问题驱动、平等对话、引发深度对话的方式，为学生思维真正的发生创造条件。

1. 二次开发教材，让思维找到切入点

数学教材由于篇幅有限，只能将数学概念、知识等“干货”较为简洁地呈现，具有较高的概括性和抽象性，不利于激发学生的学习兴趣。教师要根据学情对文本进行二次开发，创设贴近学生已有经验、能激发学习兴趣的问题情境，调动学生的积极性和主观能动性，敲开思维的大门，主动参与思考和学习。

例如，西师版二年级上册“用米做单位”一课，如果教师只是根据教材按部就班地介绍米尺，然后教授米和分米的单位换算，这无疑限制了学生的思维空间。学生在前面两节课已经认识了厘米和分米，知道测量需要统一长度单位，并学会了用尺测量物体。教师不妨充分利用学生已有的经验，设置“测量黑板等较长物体的长度”的操作活动，让学生感受用厘米和分米做单位测量的不便，进而引发思考有没有比厘米、分米“更大”的长度单位。这就让学生找到了思维的切入点，带着问题去学习米尺更有意义。经历这样的思维活动，学生还能进一步迁移：会不会有比米“更大”的长度单位？激发学生探索的欲望。

2. 设计精准问题，让思维落到关键处

问题是启发思考的动力，它可以引发学习主体一系列的思维活动。问题驱动的课堂教学并不是指课堂上的碎问碎答，问题的设计要有启发性、针对性和层次性，数学思维才能落到关键处。教师要根据教学目标和重难点，设计针对性强的核心问题，并时刻关注课堂生成，把握学生思维的生长点，培养学生的创新性思维。

例如，西师版五年级上册“小数乘小数”一课，学生已有整数乘小数计算的经验，并且观察能力、计算能力、归纳能力、抽象能力都有所提高，不妨创设一个问题情境：今年暑假，学校打算整改校门口和操场的两个长方形草坪，大草坪长5.8米、宽2.3米，小草坪长1.2米、宽0.8米，一共需要多少平方米的草埔？根据本节课的目标——理解小数乘小数的算理算法——通过设计精准的“问题串”，放手让学生自主探究、合作学习。“观察你的算式，和以前学过的算式比较，它有什么特点？”“尝试计算，说说你的计算过程？”“在计算算式时，你遇到了什么困难，你是怎么解决的？”“观察兩个因数的小数位数和积的位数，它们之间有什么关系？根据你的发现，总结小数乘小数的计算方法。”在整个探究过程中，学生紧紧地围绕“问题串”，借助小数乘整数的计算经验，通过独立思考和小组合作交流，自主习得小数乘小数的计算方法，理解小数乘法与整数乘法之间的区别与联系，理解小数乘法的算理，全面、准确地总结出小数乘法的计算法则。

3. 创造和谐学习环境，让思维碰撞成为可能

数学学习实际上是教师与学生、学生与学生、学生与文本、学生与自己之间的对话交流活动。学习活动应该在交互性和动态性的和谐环境中开展，充分发挥学生学习的自主性，让思维自由发声，把教学过程变成师生、生生的思维碰撞，情感、方法、思想交流和学习的过程。和谐的学习环境的核心是亲和性、融洽性、创造性、自主性、生态有机性受到最大限度的重视和得到最大限度的强化 [2]。其次要互动多样化，包括师生、生生、生本之间的对话和学生跟自己的对话（内省）。最后教师要处理好数学学习“动态”过程，即学生的生成。如果学生的生成并不在本节课计划之内，要根据学情恰当处理，不能扼杀学生的思维和兴趣。

4. 引导深度对话，让思维走到更深处

思维的碰撞让思维多样化，思维的深度对话让思维深刻化，让思维更接近事物的本质，让思维更具深刻性。通过师生、生生之间的分享、质疑、辨析，由表及里，去伪存真，找到多样化思维之间的共性，发展思维的深度。

例如，西师版六年级上册“比的认识”一课，通过兑蜂蜜水的情境引入，学生认识了比及其各部分名称，教师直接通过两个情境追问比的含义。

情境一：兑蜂蜜水。

师：比表示水和蜂蜜两个量什么关系？

生：表示水和蜂蜜两个量的倍数关系。

情境二：给出两种动物的路程和时间数据，算比值。

师：水和蜂蜜的单位一样，路程和时间的单位不一样，它们的比值是什么？

生：路程除以时间等于速度，这个比值就是速度。

师：通过这两个问题，比不仅可以表示两个量之间的倍数关系，还可以产生新的量，如速度（单位：m/s）。你还可以举一些例子吗？

生：工作总量∶工作时间=工作效率。

生：总价∶数量=单价。

……

比的概念虽然只有短短一句话，但是其内涵大有乾坤。只有通过这样刨根问底式的深度对话，才能让学生的思维得以发散，再聚焦，理解数学的本质。

■二、思维可视化策略——鼓励多元表征

美国NCTM在2000年的《学校数学课程标准与原则》中指出：不同的表征将导致不同的思维方式，建议学生不仅应该学会在问题解决过程中选择、使用与转化各种数学表征，而且能够在不同的表征之间建立广泛的联系 [3]。多元表征不仅能够让学生理解数学知识的本质，而且能完善学生的数学知识结构。因此，在数学教学中，鼓励学生运用图形、操作、语言等多元表征来表达自己的数学思维，实现不同表征之间的相互转换，从横向（不同表征之间的沟通）和纵向（新表征在表征系统所处的地位）理解数学的本质。

1. 动手画图——让思维直观形象

图形既是数学研究对象，又是研究数学的手段。图形的直观性，使复杂的问题简单化，抽象的问题具体化，促进学生观察能力和思维能力的发展。

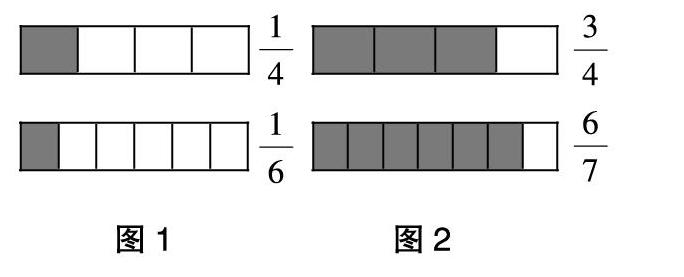
例如，西师版三年级上册“分数的大小比较”一课，根据分数的意义，分母相同也就是分的份数一样，分子不同就是取得的份数不同，份数越多，分子越大，这个分数就越大。在拓展练习时，比较■和■，部分学生想到分比萨，人数越多，每个人分到的那一份就越少;还有部分学生画图表示，思维过程直观形象（图1），通过涂色部分直接判断出■大于■。在比较■和■时，有的学生用逆向思维：一个比萨，吃了它的■，还剩它的■;同样的比萨，吃了它的■，还剩它的■。■比■多，说明■小于■。这部分学生的思维具有高度的抽象性和逻辑性。有部分学生采用画图的形式（图2），直观地判断涂色部分的多少来比较异分母分数的大小，即■小于■。通过作图，教师既了解了学生元认知策略的使用——把图形作为分析问题的策略——又了解学生的思维过程和知识的理解程度。

2. 动手操作——让思维生动清晰

美国著名的教育学家杜威主张“做”中学，强调经验源于活动，学生在做的过程中发生思考，习得经验。我国著名的教育学家陶行知在他的生活教育理论中也提倡在“做”中获得知识。可见，操作活动是学习的重要形式，能使学生思维活动的过程外显化。通过可视化的操作路径，学生更容易理解，教师更好把握学生的思维过程，调整教学策略。

低段的学生处于具体运算阶段，抽象思维较弱，尤其是对认数、概念、常见量等知识的理解时，需要调动学生的多重感知器官和借助学具等各种具体事物的支持。通过比一比、剪一剪、折一折、分一分、掂一掂等形式的操作，使抽象知识直观化、具体化。如在学习“认识厘米”时，让学生用手指比画1厘米的长度，引导学生找到自己身体上接近1厘米的部位（拇指的宽度），将抽象的长度单位形象化，感受1厘米的“短”，建立量感。

高年级的学生已经具备一定的知识、方法，抽象能力得到发展，可以设计探究性操作型活动。通过观察、实验、计算、测量、作图以及列表等操作手段，独立思考，合作探究，归纳概括，得出结论。在操作过程中，可以渗透数形结合、转化、归纳、类比、极限等数学思想，发展数学思维。如“长方形的体积”一课，可以设计如下探究操作：

（1）猜想：长方体的体积与什么有关？

（2）验证：小组合作探究。

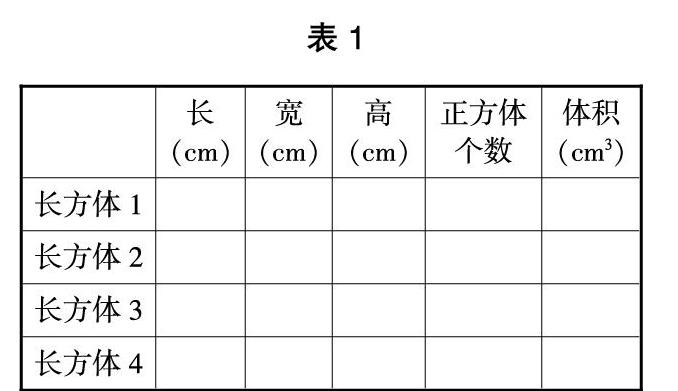
1）操作探索：用组内的12个体积为1立方厘米的小正方体拼成形状不同的长方体，每拼成一种就记录下长方体的长、宽、高和体积各是多少，填写在表格中。

2）观察发现：

①这些长方体有什么共同点？有什么不同点？

②为什么这些长方体的形状不同而体积相同？

③观察表格并讨论：长方体的体积与长方体的长、宽、高之间有什么关系。

④归纳长方体的体积计算公式：长方体的体积=______。

3. 动口表达——让思维深刻严谨

苏联心理学家维果茨基在其著作《思维与语言》 [4]中讨论了语言和思维间的关系，他认为语言是思维的外壳。史宁中教授说过“数学是思维的体操”。可见，数学、思维与语言是紧密结合的。通过语言表达，教师可以清晰把握学生的思维漏洞和思维深度。同时，学生的自由表达，生生之间的质疑辨析，也是思维不断走向严谨、深刻和批判的过程。

例如，西师版三年级下册“轴对称”一课，学生在说明长方形是轴对称图形这一环节时，出现了这样的对话：

生1：我把长方形对折，发现两条长完全重合，所以长方形是轴对称图形。同学们同意吗？（学生鼓掌表示同意）

生2：我还有一种验证方法，我把长方形对折，发现两条宽完全重合，所以长方形是轴对称图形。（学生鼓掌表示同意）

生3：我还有一种验证方法，我用剪刀把长方形沿着斜边剪开（对角线），变成两个完全重合的三角形，所以长方形是轴对称图形。

师：同学们同意吗？

生4：为什么要剪开？剪开就不能说明它是对折重合了。

师：谁听明白了？还有想说的吗？

生5：就是一个图形先要对折，然后观察它们对折后是否重合。他（生3）没有对折，不能因为重合就说是轴对称图形。（学生鼓掌）

师：你（生3）同意吗？（还是有点疑惑）

师：有哪位同学能更直观地用图向他解释？

生6：你把长方形沿着你减的那条斜边对折，它们不是完全重合的。所以长方形不是轴对称图形。（学生有异议）

生7：但是它横着和竖着对折都能重合，所以长方形是轴对称图形。

师：这个同学说得真好，确实，一个图形，只要对折出现完全重合，就是轴对称图形。还有想说的吗？

生8：其实他（生3）把长方形剪下两个三角形，把一个三角形反过来后才是完全重合的，根本不是对折，这样的判断是错的。

师：你的思考真细致。确实，他（生3）不是把剪下的三角形沿着对角线对折，而是将三角形旋转后使它们重合。现在你（生3）明白了吗？

……

从学生的表达、质疑和辨析中，学生的思维呈现在教师面前，教师可以及时把握学生的思维，及时地进行引导和纠正。自由的师生、生生的深度对话，有助于培养思维的严谨性、深刻性、批判性、创造性和灵活性，让数学思维真正发生，让教学更具思维的广度与深度。

图形、操作、语言表达等外显表征形式能促进数学知识的意义建构，增强学生发现与提出问题、分析与解决问题、归纳概括与对比分析的能力，发展思维的深刻性、严谨性、批判性和创造性，促进综合性思维的发展，培养学生的数学核心素养。

参考文献：

[1]  陈云中. 数学思维教学的研究与实践[D]. 江西师范大学，2004.

[2]  胡春燕. 新课程理论下的数学学习环境研究[D]. 重庆师范大学，2004.

[3]  郑毓信. 课改背景下的数学教育研究：回顾与展望[M]. 上海：上海教育出版社，2012.

[4]  列维·谢苗诺维奇·维果斯基. 李維译. 思维与语言[M]. 浙江：浙江教育出版社，2010.