基于模糊可拓集的特长隧道施工风险评估

王金梁， 王道隆， 陈祖斌， 黄亚娥

(1.中交路桥华南工程有限公司， 广东 清远 528400；2.浙江海洋大学， 浙江 舟山 316000)

由于隧道工程的特殊性和复杂性，施工事故发生的可能性较大。特长隧道施工事故一旦发生，将不可避免地造成大量人员和财力损失。为确保隧道施工的可靠性和人员的生命安全，需对隧道施工风险进行准确评估。吴杰等利用模糊隶属度，通过层次分析法(AHP)计算山区公路隧道施工风险评价指标的权重，并求得各指标层的关联度。郝德亮等采用AHP法确定隧道主要风险，结合风险矩阵PC法和多级可拓法进行综合评估。李恒等利用模糊数学理论构造隶属函数得出模糊一致性判断矩阵，采用AHP法计算钢箱梁桥各层评价指标的权重，最终得到钢箱梁桥的质量等级。马光金采用故障树法对盾构隧道施工风险进行分析，使用灰色关联法对其进行关联分析，找出需要重视和规避的基本事件并提出预防和处理方案。现有研究大多存在权重确定主观性过强的问题，且指标值的选取多为实数，而实际工程中参数取值往往是具有模糊性的区间值。采用模糊可拓集方法可对定性指标进行定量化分析。基于此，该文基于AHP法和模糊可拓集理论对特长隧道施工风险进行评估，结合广东省从化至清远连州高速公路车子岭隧道工程进行验证。

1 建立评估指标体系

分析影响特长隧道施工风险的各种因素，参考现有研究成果，结合车子岭隧道工程的结构特征，构建表1所示特长隧道施工风险评估指标体系。

2 AHP法确定评价指标权重

2.1 评价尺度

参考文献[13]，得到表2所示评价标准。

表1 特长隧道施工风险评估指标体系

表2 AHP评价尺度

2.2 判断矩阵

按照层次结构模型，每一层元素都以相邻上一层次各元素为基准，按表2所示评价尺度各元素为基准，设判断矩阵为A，有：

(aij)n×n

(1)

按AW=λmaxW求解特征根，并对计算出的W作归一化处理和一致性检验。步骤如下：

(1) 按式(2)计算判断矩阵每行元素的乘积：

(2)

(2) 按式(3)计算mi的n次方根：

(3)

(4)

(4) 按式(5)计算最大特征根：

(5)

式中：(Aw)i表示向量Aw的第i个分量。

2.3 判断矩阵一致性检验

一致性检验公式为：

式中：CI为一致性检验指标，CI=(λmax-n)/(n-1)；RI为随机一致性指标，其取值见表3。

表3 随机一致性指标的取值

当CI<0.1时，矩阵A符合要求；否则，重新调整取值进行计算，直到满足一致性检验为止。

2.4 计算权重向量

在满足一致性检验的条件下，即可求得各层评估指标的权重向量。

3 构建隧道模糊可拓集综合评估模型

模糊可拓集综合评估模型以有序三元组R=(事物,特征,量值)=(N,C,V)作为描述事物的物元，将待评价指标进行定量化分析，然后根据权重计算各指标与评价目标的关联度，最后根据模糊数学中的最大隶属度原则得出评价等级。

3.1 确定评价物元模型的经典域与节域

经典域定义为：

(6)

式中：Nj为特长隧道施工风险评估第j(j=1,2,…,m)个等级；ci为特长隧道施工风险评价第i(i=1,2,…,m)个评价指标；vij为隧道施工风险属于第j个等级时对应ci的指标量值〈aij，bij〉，其为特征ci属于待评指标的经典域。

节域定义为：

(7)

式中：P为所有特长隧道施工风险评估等级；〈aip,bip〉为某一指标ci的取值范围，即节域。

3.2 确定隧道施工风险可拓评价物元

隧道施工风险可拓评价物元定义为：

(8)

式中：T为待评价特长隧道施工风险指标；vi为指标量化后的数值。

3.3 指标的无量纲化处理

为使不同单位的评价指标具有可比性，对各层指标进行无量纲化处理。对于越小越好型指标，无量纲化处理公式为：

(9)

对于越大越好型指标，无量纲化处理公式为：

(10)

3.4 计算关联度

设vik为隧道施工风险关于ci的量值，vij=〈aij,bij〉,vip=〈aip,bip〉，隧道施工风险关于经典域及节域的距为：

(11)

按式(12)计算各指标与评价目标的关联度：

(12)

3.5 风险评价

根据式(12)所得关联度及利用式(1)～(5)得到的权重对特长隧道施工风险等级进行可拓评价：

k(Ni)=(wj1,wj2,…,wjk)·

(i=1,2,3)

(13)

k(N)=w1·k(N1)+w2·k(N2)+w3·

k(N3)=(k1(N),k2(N),k3(N),k4(N))

(14)

由模糊数学中最大隶属度原则，按照式(15)便可确定待评特长隧道施工风险等级。

(15)

4 实例验证

4.1 工程概况

车子岭隧道位于清远英德市水边镇境内，进口位于水边镇黄泥洞地界，出口位于水边镇崩江潭地界。为分离式隧道，左线起讫里程为ZK82+925—ZK84+070，长1 145 m，最大埋深139.3 m；右线起讫里程为K82+910—K84+077，长1 167 m，最大埋深126 m。隧道总体走向方位角约304°。进口、出口均采用端墙式洞门。

4.2 指标权重计算

邀请10位隧道工程领域专家学者对隧道施工风险评价指标的重要性进行打分，根据专家的评分，利用AHP法求出各指标的权重(见表4)。

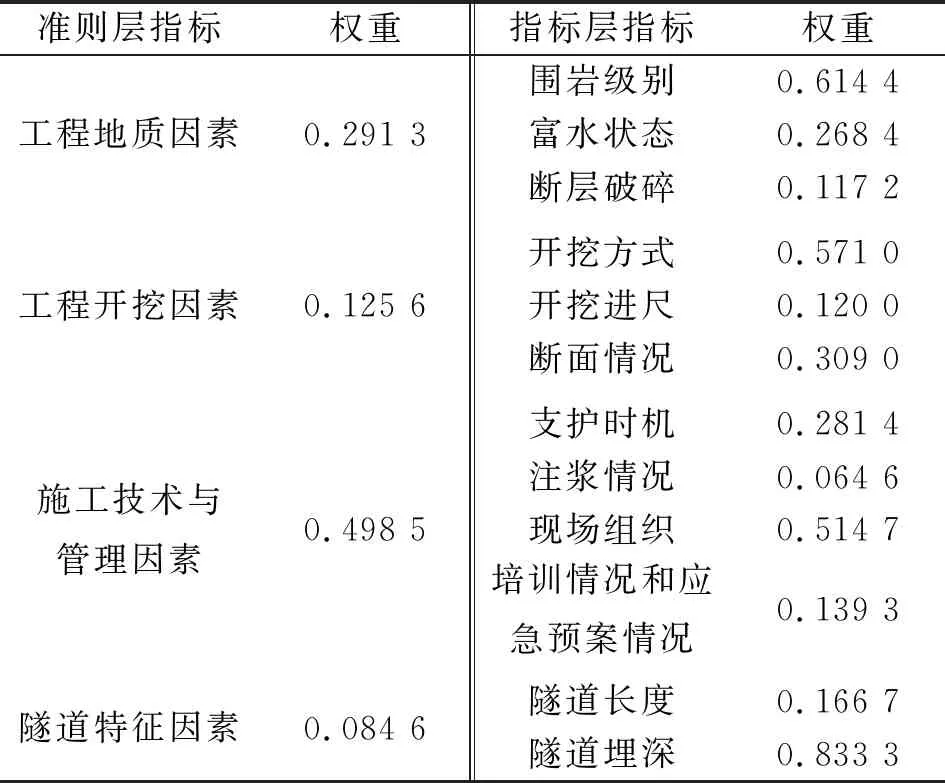
表4 特长隧道施工风险评价指标的权重

4.3 确定风险等级评定标准与分类

将隧道施工风险划分为4个等级(见表5)。对于定性指标，评价等级Ⅰ、Ⅱ、Ⅲ、Ⅳ级的量化值分别为(0，0.25)、(0.25，0.5)、(0.5，0.75)、(0.75，1.0)。对于定量指标，则进行无量纲化处理，将评价量值划分到0～1.0内，使各评价指标之间具备可比性。风险指标无量纲化处理前后的结果见表6、表7。

表5 隧道施工风险等级

4.4 确定隧道施工风险物元模型

经典域和节域为：

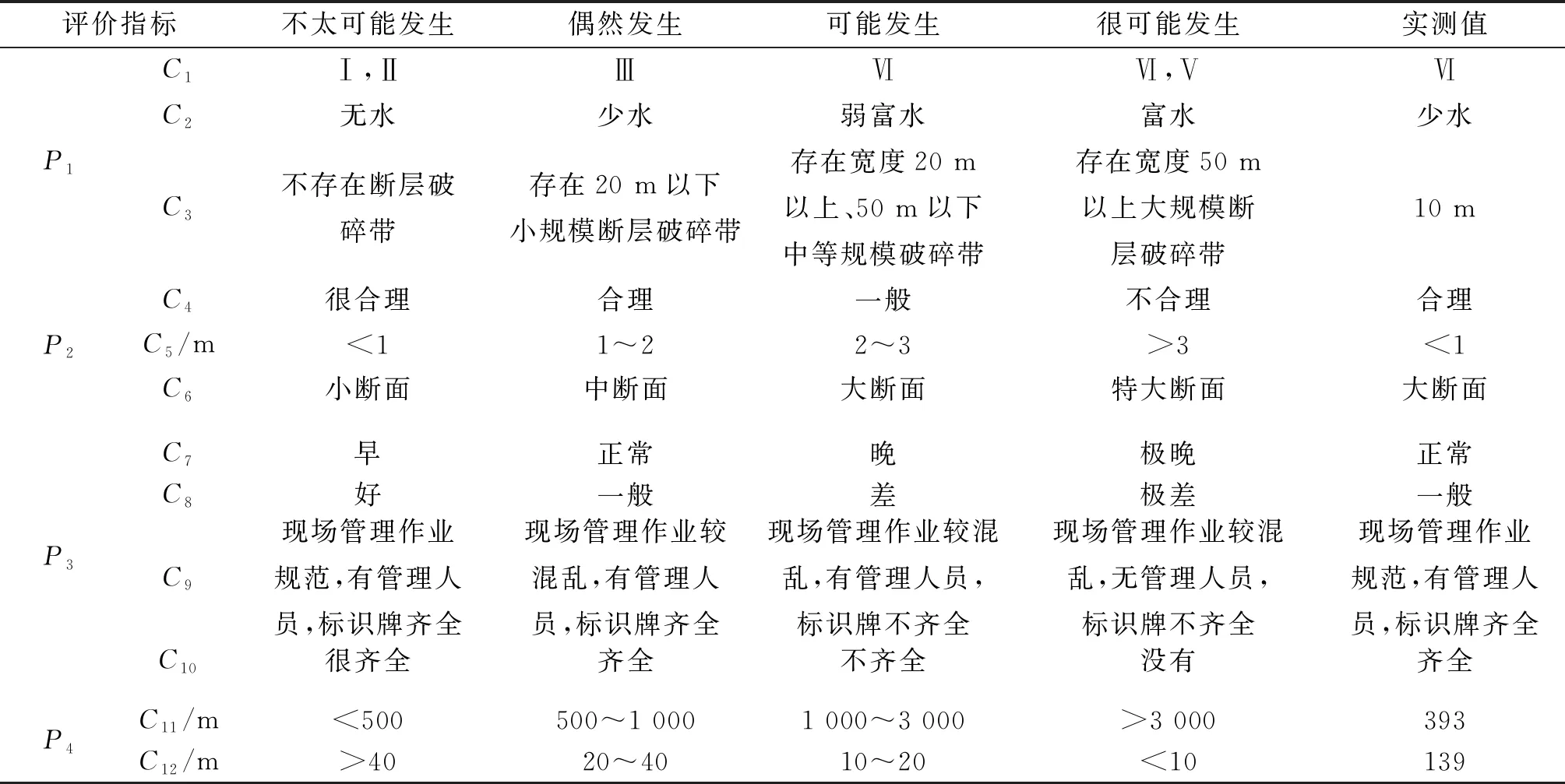
表6 隧道施工风险评价指标无量纲化前的结果

表7 隧道施工风险评价指标无量纲化处理结果

根据式(11)、式(12)计算各评价指标的风险关联度，结果见表8。

表8 各评价指标的风险关联度

4.5 模糊可拓评价

k(N1)=(0.614 4,0.268 4,0.117 2)·

(-0.409 0，0.027 7，0.201 2，-0.349 8)

同理得：

k(N2)=(-0.242 1,0.133 7,-0.078 7,-0.457 3)

k(N3)=(0.123 4,-0.014 1,-0.497 4,-0.664 9)

k(N4)=(0.172 6,-0.172 6,-0.452 8,-0.734 3)

隧道施工风险发生可能性等级的关联度为：

k(N)=(0.291 3,0.125 6,0.498 5,0.084 6)·

(-0.073 4，0.003 2，-0.237 5，-0.552 9)

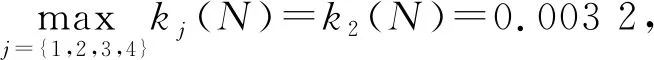
5 结语

该文采用模糊可拓集方法，从工程地质、工程开挖、施工技术与管理和隧道特征4个方面及其12个影响因素进行分析，建立特长隧道施工风险评价指标体系，通过计算指标与评价等级之间的关联度，准确描述影响隧道施工各因素属于某一等级的程度，对特长隧道施工风险进行客观评估。将该模糊可拓集模型应用于广东省从化至清远连州高速公路车子岭隧道工程施工阶段安全风险评估，得出风险发生可能性为二级，评估结果与现场实际情况相符，说明该模型具有一定可行性。模糊可拓集评估模型量化了特长隧道施工风险发生可能性，有利于降低其事故发生风险。