基于ANSYS的某在役悬索桥砼主塔结构性能分析

朱德权， 罗向荣， 左传艺

(1.长沙理工大学 土木工程学院， 湖南 长沙 410114；2.中国恩菲工程技术有限公司， 北京 100038；3.贵州省交通规划勘察设计研究院股份有限公司， 贵州 贵阳 550001)

桥梁在运营期承受大量荷载，其中恒载和活载属于直接荷载，砼收缩徐变、温度效应属于非直接荷载。对于桥梁砼构件，温度效应导致的裂缝是其主要病害之一，大部分砼桥梁裂缝的出现与温度效应有关。因此，对于该类病害的分析，除进行恒载、活载作用下结构分析外，还需进行温度效应分析。

悬索桥是桥梁结构体系中跨越能力最大的桥型，其主要受力构件是主缆与吊杆组成的缆索系统、加劲梁及桥塔和锚碇结构，其中主塔主要由钢材或砼建成。运营期桥塔砼出现裂缝是悬索桥的主要病害之一。某在役悬索桥于1997年建成通车，砼桥塔已出现竖向裂缝，为给桥梁加固提供依据，对桥塔单独进行建模分析，分析主塔在恒载、活载及温度作用下的结构性能。

1 工程背景

该桥为主跨450 m双塔单跨两饺悬索桥，主缆跨度组合为164.5 m+450.0 m+130.0 m，矢跨比为1/11。水平面内在横向由跨中以曲线向外伸展，形成外张式，外张矢度为3.25/450=1/138.5，外张角为4°9′37″。加劲梁采用平弦三角形钢桁架，桁高和节间长度均为3.0 m，高跨比为1/150，主桁中心距14.0 m，宽跨比为1/32.14。桁架杆件采用焊接H形截面，宽360 mm，板厚12～16 mm。横梁位于吊杆处，按6 m间距设置，采用构造为型钢组成的三角型桁架，桥面板采用预制砼板加现浇纤维砼。主桥大缆由61股91φ5.2高强镀锌钢丝束采用PPWS法形成，外径43.8 cm。吊杆为φ120成品扭绞型拉索。南北索塔都采用钢筋砼H形塔，塔柱壁厚为60～100 cm，北、南岸塔高分别为98.0和83.0 m，塔柱中心距20.5 m。

2 计算模型与荷载工况

2.1 索塔分析计算参数

2.1.1 荷载

荷载如下：1) 恒载。为全桥自重及二期恒载作用下塔顶荷载。2) 活载。为在汽车-20级、挂-100作用下塔顶荷载。3) 砼收缩徐变。考虑结构砼收缩徐变对索塔的附加内力。4) 温差Ⅰ。索塔温度外高内低，温差+10 ℃。5) 温差Ⅱ。索塔温度内高外低，温差-10 ℃。

2.1.2 材料

桥塔砼材料参数见表1。

表1 桥塔砼材料参数

2.2 荷载工况

桥梁运营期除恒载、活载外，温度效应也是影响桥梁受力的重要因素。鉴于该桥索塔的实际病害为运营期裂缝，假设2种温差条件(温差Ⅰ、Ⅱ)对结构进行分析。为正确模拟索塔真实的受力状态，将全桥结构的恒载、活载及砼收缩徐变对索塔产生的效应以荷载的形式加载在索塔上。分3种工况进行分析，工况1为恒载+活载+砼收缩徐变，工况2为工况1+温差Ⅰ，工况3为工况1+温差Ⅱ。

2.3 有限元模型

MIDAS/Civil整体分析模型采用每一节点6个自由度的杆系单元，主缆及吊索采用缆索单元，只有轴向自由度，再配以几何非线性(见图1)。由于边跨引桥独立于大桥，无需模拟。

主梁由北岸桥塔伸缩缝起至南岸桥塔伸缩缝止为桁架结构。主梁桁架杆件采用梁单元模拟，因其节点联结有足够刚度，主桁梁节点均为固接，没有引入任何铰接。桥塔由基础底面起，包括塔柱和横梁。主缆为北岸桥塔理论散索点至南岸桥塔理论散索点。吊索由主梁至主缆。

对于桥塔砼结构的局部分析，采用ANSYS建立索塔实体模型，分成热分析和结构分析依次计算。桥塔实体模型的建立：先采用Solid87单元建立索塔温度场模型，定义砼材料的特性值和边界条件得到热分析模型，通过分析把温差荷载转化成结构温度场；再把Solid87单元转化成Solid92结构单元，建立桥塔结构分析实体模型，施加由MIDAS/Civil整体分析得到的塔顶恒载、活载作用结果，并导入ANSYS热分析得到的结果，通过对该模型的分析运算，得到各荷载工况下索塔应力分布。

3 计算结果与分析

3.1 整体受力分析

该文重点分析桥塔的结构性能，故不列出主缆和主梁的分析结果，只给出主塔在恒载、活载组合及最不利荷载组合作用下的受力结果：1) 恒载和活载组合下，北岸塔顶最大内力为93.5 MN，南岸塔顶最大内力为100.8 MN。极限状态最不利荷载组合下，北岸塔顶最大内力为113.7 MN，南岸塔顶最大内力为125.4 MN。2) 恒载和活载组合下，北岸塔顶最大位移为0.54 m，南岸塔顶最大位移为0.45 m。极限状态最不利荷载组合下，北岸塔顶最大位移为0.69 m，南岸塔顶最大位移为0.58 m。

由于塔柱为偏心受压构件，通过塔顶内力和位移可看出，南侧塔柱受力更为不利。

3.2 索塔局部分析

该桥南北索塔受力状况大同小异，选择所受恒载和活载较大、受力更为不利的南索塔进行分析。为便于观察索塔表面应力结果，在索塔塔柱侧面(近横梁侧)中心设置从底至顶的应力结果观察路径A，在索塔侧面(背横梁侧)中心设置从底至顶的应力结果观察路径C，在索塔顺桥向一侧塔柱正面中心设置从底至顶的应力结果观察路径B，在索塔顺桥向一侧塔柱背面中心设置从底至顶的应力结果观察路径D(见图2)。压应力为负，拉应力为正。

图2 索塔应力观察路径示意图

3.2.1 工况1作用结果

图3、图4为工况1作用下索塔第一、第三主应力云图。由图3、图4可知：在恒载、活载及砼收缩徐变效应作用下，索塔侧面的第一主应力较大，最大达0.9 MPa；索塔正面及背面的第一主应力较小，远小于使砼开裂的应力。

根据应力计算结果绘制桥塔结构应力路径图(见图5～8)。由图5～8可知：工况1作用下，沿路径A的第一主应力最大发生在37.314 m处(下横梁附近)，第三主应力最大发生在24.876 m处(下横梁附近)；沿路径B的第一主应力最大发生在74.628 m处(上横梁附近)，第三主应力最大发生在16.584 m处(塔底附近)；沿路径C的第一主应力最大发生在29.022 m处(下横梁附近)，第三主应力最大发生在塔底部附近；沿路径D的第一主应力最大发生在29.022 m处(下横梁附近)，第三主应力最大发生在塔底部附近。

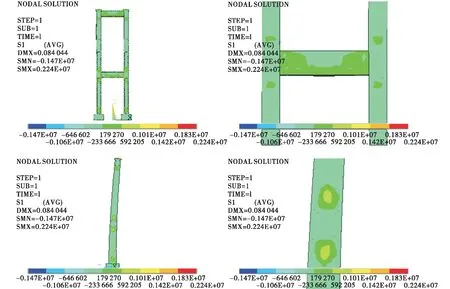
图3 工况1作用下索塔第一主应力云图(单位：Pa)

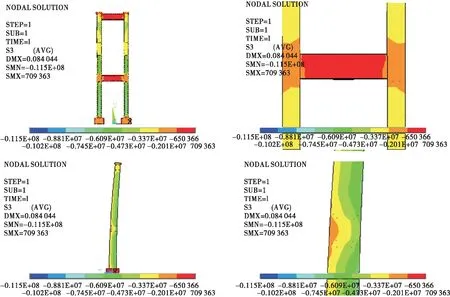
图4 工况1作用下索塔第三主应力云图(单位：Pa)

3.2.2 工况1+温差Ⅰ作用结果

图9、图10为工况1+温差Ⅰ作用下索塔第一、第三主应力云图。由图9、图10可知：在工况1+温差I作用下，在外侧温度高于内侧温度时，索塔外表面的拉应力不仅没有增加，反而有所减少。可见，外高内低的温差对索塔产生一个“紧箍力”，使索塔结构处于三向应力状态，对结构有利。

图5 工况1作用下路径A应力图

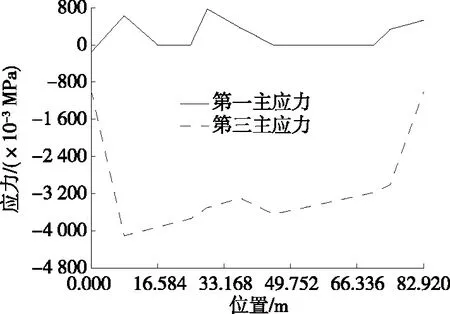
图7 工况1作用下路径C应力图

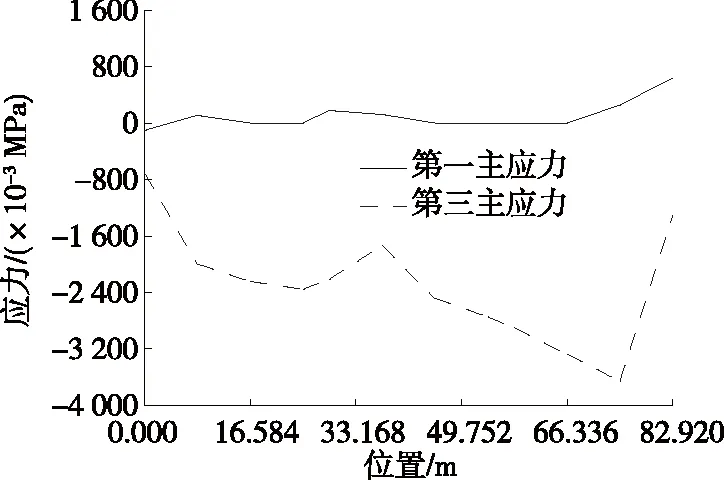
图6 工况1作用下路径B应力图

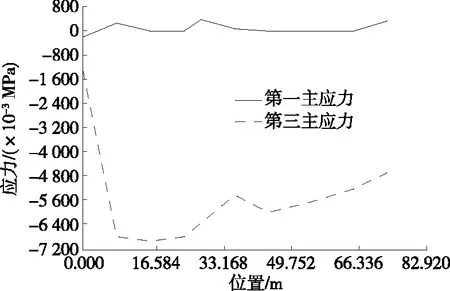
图8 工况1作用下路径D应力图

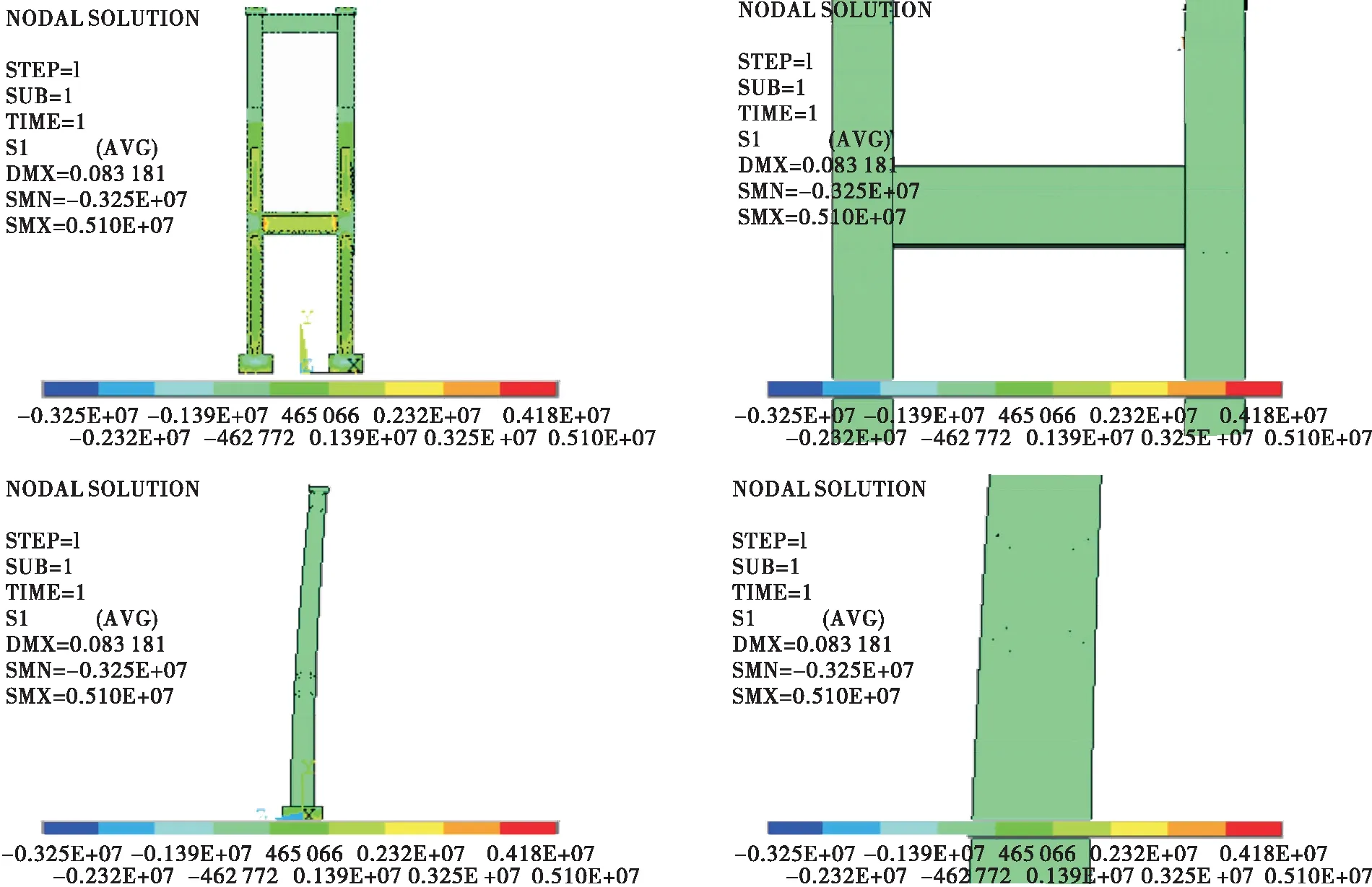
图9 工况1+温差Ⅰ作用下索塔第一主应力云图(单位：Pa)

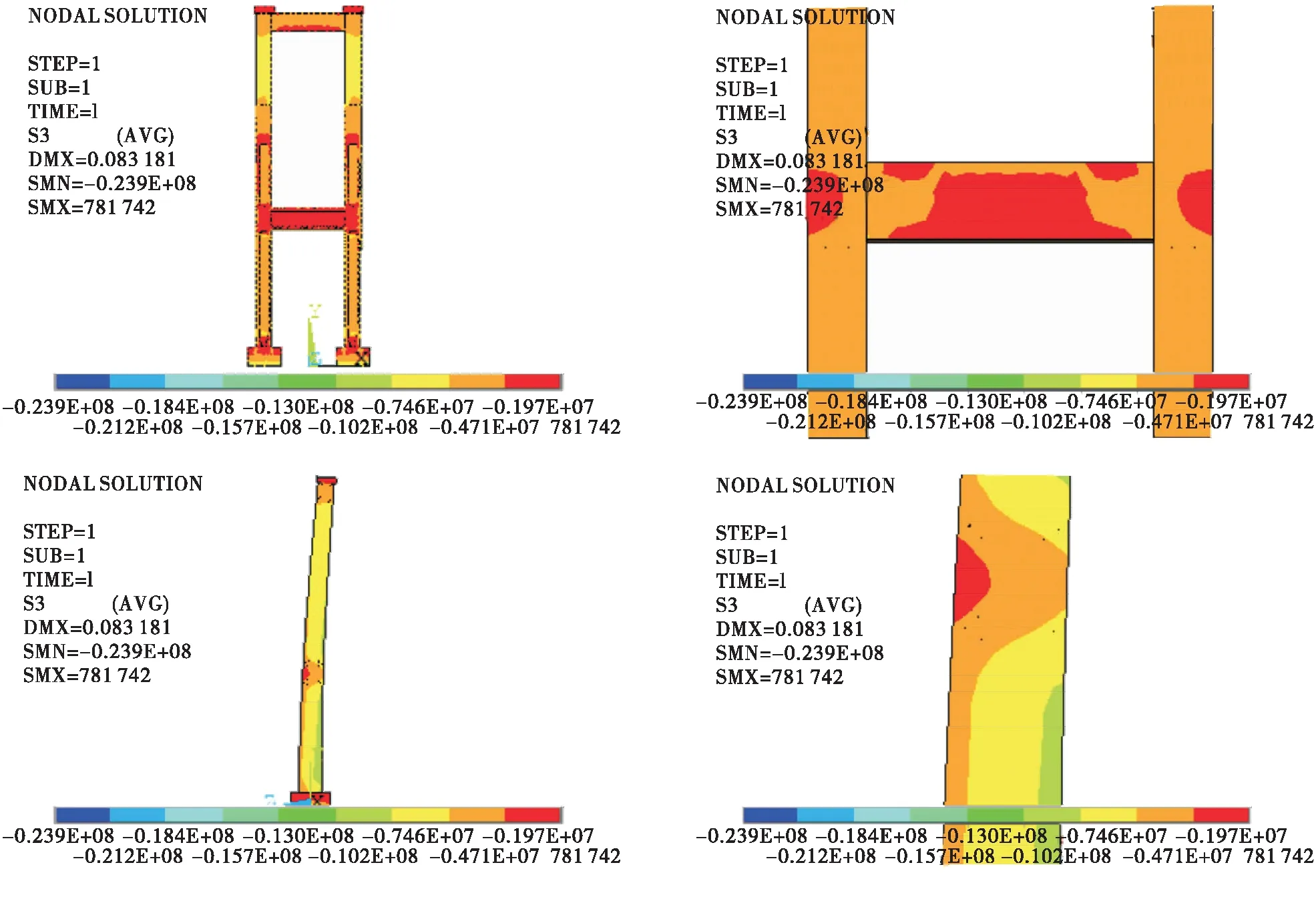
图10 工况1+温Ⅰ作用下索塔第三主应力云图(单位：Pa)

工况1+温差Ⅰ作用下桥塔结构应力路径见图11～14。由图11～14可知：工况1+温差Ⅰ作用下，沿路径A的第一主应力均较小，第三主应力最大发生在塔底部附近；沿路径B的第一主应力大多数表现为压应力且都较小，第三主应力最大发生在塔底部附近；沿路径C的第一主应力均较小，第三主应力最大发生在塔底部附近；沿路径D的第一主应力大多数表现为压应力且都较小，第三主应力最大发生在塔底部附近。

图11 工况1+温差Ⅰ作用下路径A应力图

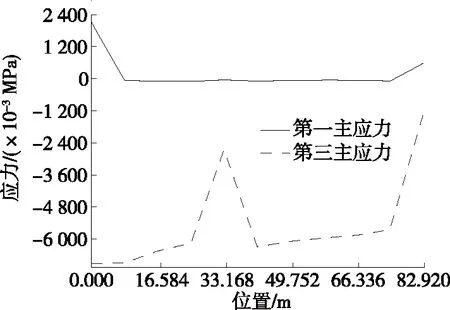
图13 工况1+温差Ⅰ作用下路径C应力图

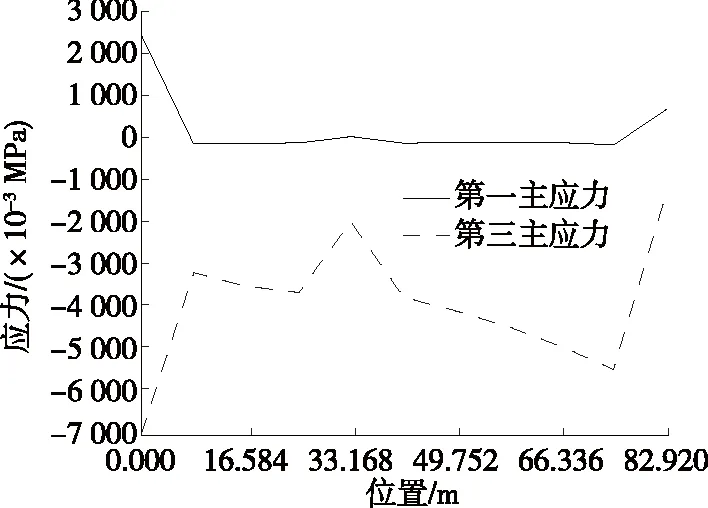
图12 工况1+温差Ⅰ作用下路径B应力图

图14 工况1+温差Ⅰ作用下路径D应力图

3.2.3 工况1+温差Ⅱ作用结果

图15、图16为工况1+温差Ⅱ作用下索塔第一、第三主应力云图。由图15、图16可知：工况1+温差Ⅱ作用下，温差为-10 ℃时，索塔侧面中心的拉应力均已超过砼的抗拉强度设计值，侧面中心应力值大于正面中心应力值。

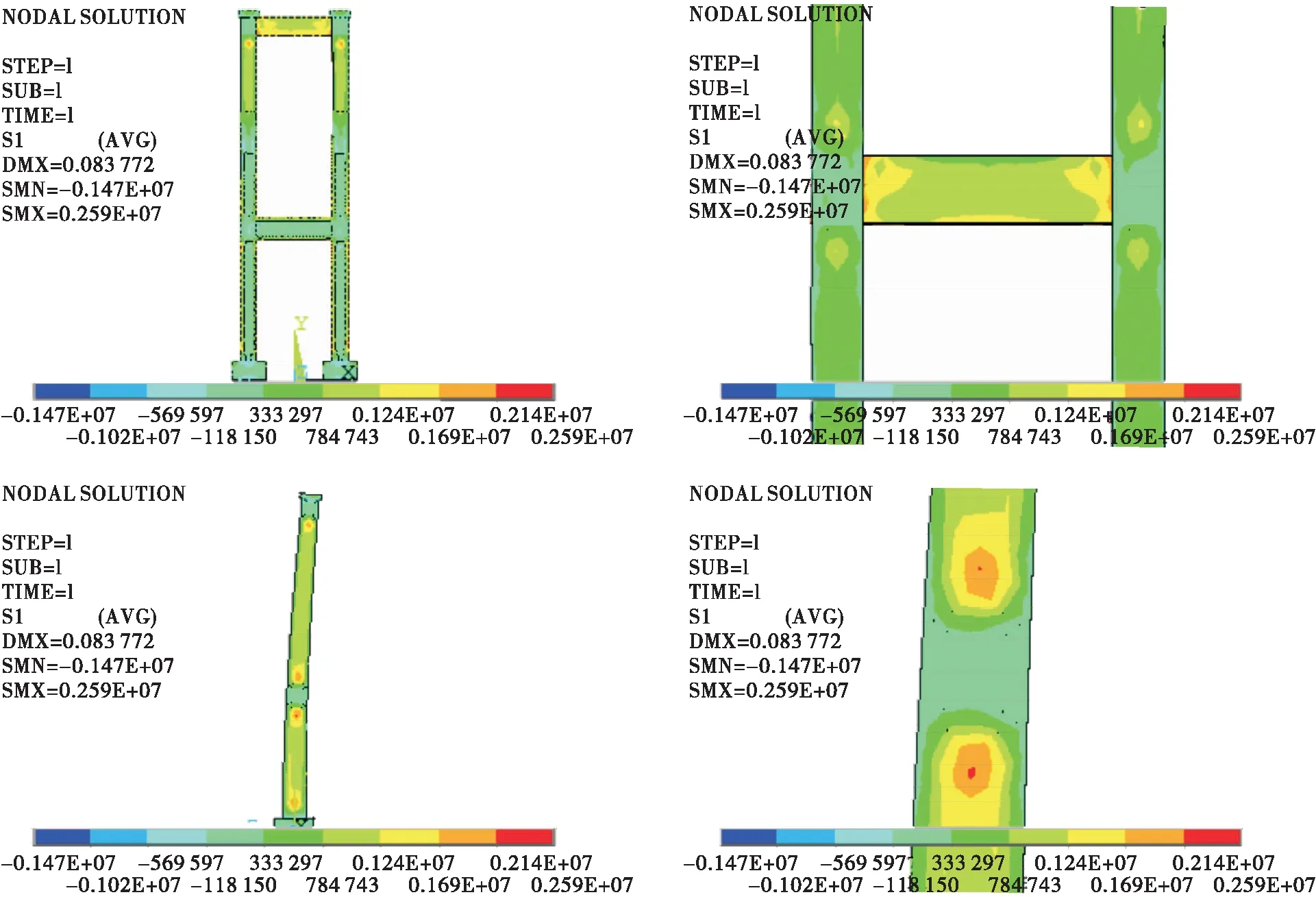
图15 工况1+温差Ⅱ作用下索塔第一主应力云图(单位：Pa)

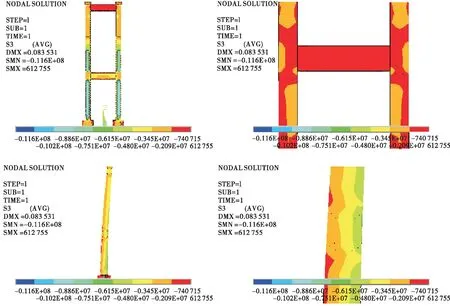
图16 工况1+温差Ⅱ作用下索塔第三主应力云图(单位：Pa)

工况1+温差Ⅱ作用下桥塔结构应力路径见图17～20。由图17～20可知：沿路径A的第一主应力最大发生在37.314 m处(下横梁附近)，且附近应力值均已超过30号砼抗拉强度设计值(1.75 MPa)；第三主应力最大发生在24.876 m处。沿路径B的第一主应力最大发生在74.628 m处(上横梁附近)，第三主应力最大发生在74.628 m处(上横梁附近)。沿路径C的第一主应力最大发生29.014 m处，且附近应力值均已超过30号砼抗拉强度设计值；第三主应力最大发生在塔底部附近。沿路径D的第一主应力最大发生在74.628 m处，第三主应力最大发生在塔底部附近。

图17 工况1+温差Ⅱ作用下路径A应力图

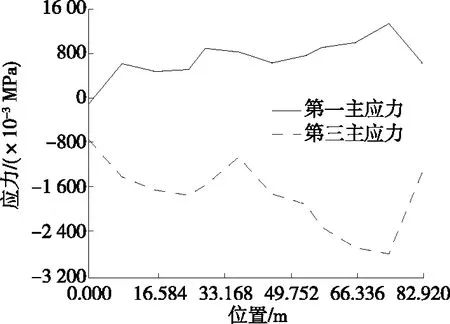
图18 工况1+温差Ⅱ作用下路径B应力图

图19 工况1+温差Ⅱ作用下路径C应力图

图20 工况1+温差Ⅱ作用下路径D应力图

4 结论

(1) 在恒载、活载及砼收缩徐变共同作用下，由于砼具有泊松比的关系，在砼发生纵向应变时也发生横向应变，使索塔侧面(背横梁处)出现较大拉应力(0.9 MPa)。

(2) 在相同温差条件下，沿塔高方向，索塔侧面下部(下横梁附近)的第一主应力略高于上部第一主应力，即同一工况下索塔侧面下部产生裂缝的概率及裂缝大小高于上部。

(3) 在外侧温度高于内侧温度时，索塔外表面的拉应力较恒、活载而言有所减少。外高内低的温差对索塔产生一个“紧箍力”，使索塔结构处于三向应力状态，对结构有利。

(4) 内外温差对结构影响很大，特别是当温度内高外低时，在结构外表面产生的拉应力较大，会导致砼开裂。