基于柔度曲率比与遗传算法的既有钢筋砼拱桥损伤识别研究*

廖俊文， 刘京铄

(湖南水利水电职业技术学院， 湖南 长沙 410199)

既有桥梁逐渐老化及新桥因施工质量和设计技术等因素导致桥梁结构损伤，可能引发安全事故。学者们在桥梁结构损伤识别方法研究及推广应用方面进行了一系列研究，取得了非常多有意义的科研成果。但桥梁结构损伤识别研究在理论与实际应用上仍存在差异，无法精确判断桥梁结构损伤位置与程度，寻找简便、敏感度高的损伤指标，提高损伤识别速度及满足大型桥梁结构损伤识别需求是未来桥梁结构损伤识别的研究方向。该文结合柔度曲率比理论与变异遗传方法，利用结构的柔度矩阵为参数，提取柔度矩阵的柔度曲率比识别结构损伤位置；在自适应遗传算法的基础上，提出改进自适应双向变步长变异遗传算法判断结构损伤程度。

1 损伤识别基本理论与算法

1.1 柔度曲率比法

根据结构振动分析理论，结构的柔度矩阵F可表示为：

(1)

式中：n为模态阶数；ωi为第i阶模态频率；φi为归一化质量矩阵对应的第i阶模态振型。

设Fu、Fd分别表示结构损伤前、后柔度矩阵，ΔF为结构损伤前后柔度矩阵差，则：

ΔF=Fu-Fd

(2)

分别取ΔF与Fu的主对角元素，按列向量分别表示为{Δf}和{fu}：

{Δf}=diag(ΔF)

(3)

{fu}=diag(Fu)

(4)

式中：diag()表示取矩阵的主对角元素。

利用差分法计算曲率：

(5)

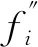
(6)

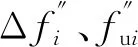
由式(6)可知：柔度曲率比与节点位置对应，由所有节点的柔度曲率比按节点顺序构成的列向量{η}称为柔度曲率比向量，当结构某节点出现损伤时，对应节点(对应位置)的柔度曲率比值发生突变，绘制柔度曲率比随节点的变化曲线(除去首、末两端节点)，曲线突变处即为结构损伤位置。

1.2 自适应双向变步长变异遗传算法

遗传算法是一种仿生优化算法，具有简单通用、鲁棒性强等优点，是求解函数优化问题的强有力工具。自适应变步长变异遗传算法是遗传算法发展中主要改进方向之一，其优势是利用搜索点处适应度函数的变化来改变个体变异的步长，提高寻优速度，使变异后的个体逼近最优解或最优解集。其局限是仅在后退搜索过程中引入变步长操作，无法改善寻优过程中向前搜索速度。

1.2.1 改进算法流程

针对自适应变步长变异遗传算法的不足进行改进，在保证后退搜索过程中提高寻优速度的前提下，在向前搜索过程中也构建变步长操作，进一步提高寻优速度。改进后算法称为自适应双向变步长变异遗传算法。其基本思想如下：比较新、旧个体的适应度值，如果新个体的适应度值大于旧个体的适应度值，则按变异步长逐次倍乘的原则沿原方向向前变异，直至新个体的适应度值小于旧个体的适应度值；然后从新个体处沿反方向按变异步长逐次减半的原则后退搜索新个体，直至新个体的适应度值大于旧个体的适应度值。算法流程(见图1)如下：

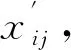
(7)

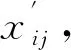
(8)

(4) 个体替换。如果新个体的适应度值小于旧个体的适应度值，则以一定概率接受它为新种群中的个体；如不满足概率要求，则重新实施正态分布扰动操作，重新进行判断。

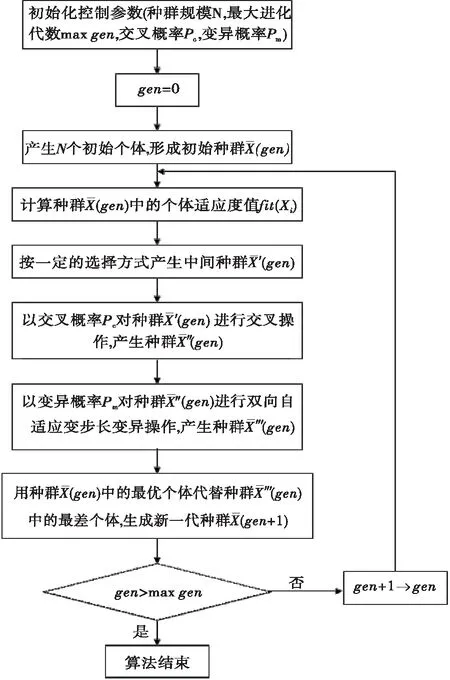
图1 自适应双向变步长变异遗传算法流程

算法的改进体现在步骤3“若Δfit(Xi)<0”继续向前搜索中，利用该步骤第1步中“令L′=2L”的功能，使向前搜索在前一次搜索的速度基础上按2n的指数幂加速前进，大大缩短向前寻优的时间；在后退搜索过程中引入变步长的操作表现在步骤3第2步中“令L′=-L/2”。

1.2.2 改进算法的效果

以一等截面简支梁为例，在已知损伤位置的情况下分两种工况，分别为单损伤(跨中位置L/2)与多损伤(L/4、L/2、3L/4三处位置)，两种工况中损伤程度均为20%。改进前后遗传算法的效果对比见表1。由表1可知：尽管改进后算法的计算精度改善并不明显，但计算效率方面提高非常明显。

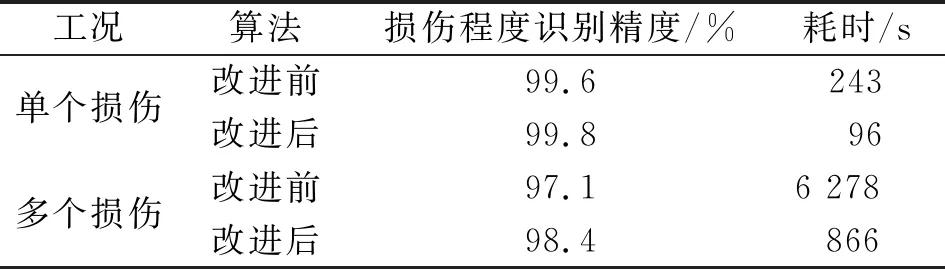
表1 遗传算法改进前后的效果对比

1.3 损伤识别过程

结合柔度曲率比理论与变异遗传方法，将结构损伤识别过程分为两步：

(1) 利用基于柔度矩阵的柔度曲率比进行损伤单元位置判断，排除无损伤单元，使之不进入下一步的损伤定量计算程序，减少损伤定量计算工作量。

(2) 利用自适应双向变步长变异遗传算法计算各损伤单元的刚度折减系数，确定其损伤程度，单元的刚度折减系数越小，则该单元的损伤越严重。

2 损伤识别分析

湖南省常宁市北门桥已服役28年，属于危桥，决定拆除。该桥为等截面悬链线无铰拱桥，拱肋截面尺寸为0.20 m×0.28 m，矢高为3.10 m，净跨径实测值为19.93 m。取其中2片拱肋作为研究对象开展结构损伤识别研究。

2.1 损伤位置识别

通过ANSYS建立桥梁拱肋三维有限元模型，采用Beam4单元。为方便有限元计算结果和试验测试结果的处理，有限元离散化时节点位置取为模态试验传感器测点布置位置，按弦长等距离划分为32个3D梁单元，共33个测点(见图2)。

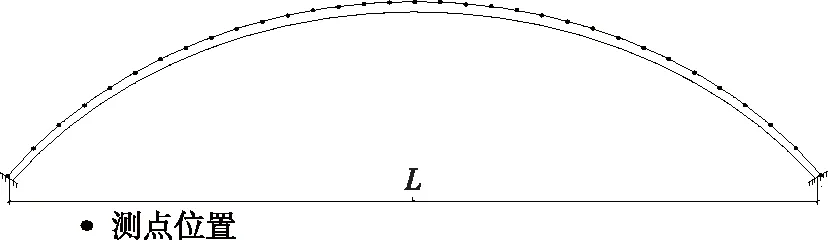
图2 拱肋模态试验测点位置(有限元单元划分)

拱肋模态测试试验流程见文献[12]。测试中采用锤击激励法获取拱肋的试验模态参数(参考文献[12]中表4.3)，并将试验测试结果作为拱肋损伤状态值；采用ANSYS建立拱肋有限元模型作为无损伤参照对象，模态参数见文献[12]中表4.4。提取拱肋前3阶模态结果计算柔度曲率比，并绘出其随节点位置变化趋势图(见图3)。

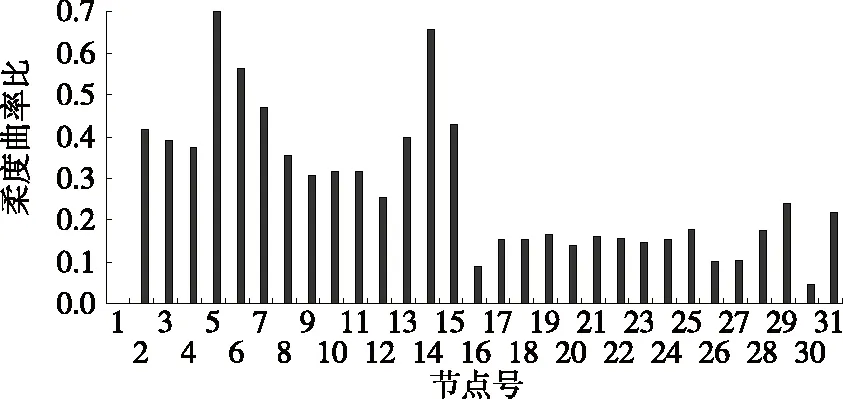
图3 拱肋的柔度曲率比随节点的变化

由图3可知：拱肋均已出现刚度下降现象。受交通流量、荷载、自然环境及人为不合理使用等因素的影响，拱肋出现砼开裂、劣化、内部裂缝发生与扩大、钢筋锈蚀等损伤情况，导致拱肋结构刚度劣化严重。根据测试结果，拱肋所有划分节点位置均存在不同程度损伤，在下一步损伤程度识别中，应考虑将所有单元参与识别计算。

2.2 损伤程度识别

基于上述损伤识别结果，通过自适应双向变步长变异遗传算法计算各单元的刚度折减系数，确定拱肋的损伤程度。遗传算法的前处理：

(1) 选取变量指标。取所有单元的刚度折减系数作为设计变量xi(i=1,2,3,…,32)，取值区间为[0.2,1]。

(2) 定义适应度函数。以柔度曲率比为目标函数，设由遗传算法求解的柔度曲率比值为ηcal，实际测量的柔度曲率比值为ηtest，取两者的范数，表达式如下：

(9)

(3) 编码。选择实数编码描述个体，每个个体的基因位的数值就是该基因位序号对应单元的刚度折减系数xi。

(4) 选择操作。选取种群规模为100。

(5) 交叉操作。选取交叉概率Pc=0.75。

(6) 变异操作。选取变异概率Pm=0.1。

各单元的刚度折减系数见图4。由图4可知：拱肋整体刚度已下降，存在不同程度损伤。

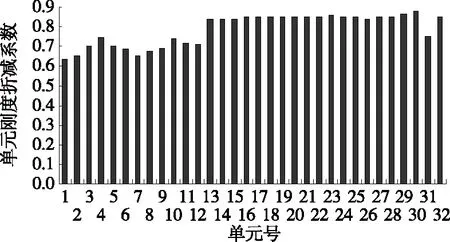
图4 拱肋的单元刚度折减系数

3 损伤识别结果对比分析

3.1 外观检测

拱肋外观评定检测结果如下：1) 拱肋从拱顶到东半拱1/4跨之间表面出现少量麻面，最大麻面面积为0.60 m×0.27 m，且有8根箍筋外露，露筋总长1.44 m。2) 拱肋初始裂缝主要分布在西半拱，裂缝走向主要沿拱背横向，从拱肋两侧沿径向延伸，延伸长度最大为72.5 mm(拱背、拱肋一侧贯通)。3) 全拱有1条横向贯通的裂缝，裂缝宽0.09 mm；有2条由于钢筋锈蚀产生的纵向裂缝，第一条缝宽0.42 mm，距西拱脚0.54～1.23 m，第二条缝宽0.50 mm，距西拱脚8.03～8.31 m(见图5)。对比图4、图5，可知搜索结果可信。

3.2 弯曲刚度反演

对比拱肋的有限元计算结果与静载试验数据，可知：在试验的前一两级荷载作用下，结构没有产生新的损伤，尚处于弹性阶段，可作为拱肋的初始状态。因此，选取静载试验第2级荷载(5.75 kN)对应的挠度值反演弯曲刚度值，然后以该值作为参考基准计算刚度折减系数，计算公式见式(10)，计算结果见表2。

图5 拱肋原始裂缝分布展开图

(10)

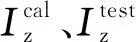
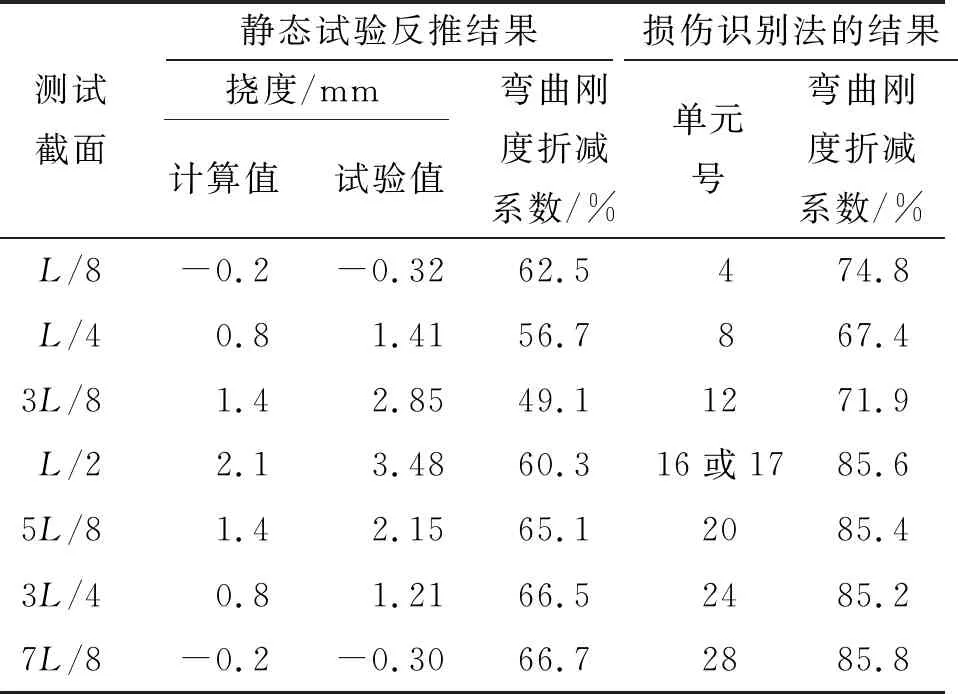
表2 由静载试验反演所得结构弯曲刚度折减系数

由表2可知：反演结果与损伤识别结果吻合很好，两种方法的计算结果基本相似，但部分单元结果存在差异。其原因为：1) 测试误差，这在整个损伤识别中都被忽略；2) 结构静态刚度值与动态刚度值并不完全一致，动力刚度一般大于静力刚度。

3.3 实体检测

针对拱肋不同位置钻取直径为10 cm的砼芯样进行材性试验，芯样的弹性模量测试值见表3。采用CANIN型钢筋锈蚀仪测量拱肋砼表面各测点与外露纵筋电位差，测量结果见表4。

由表3、表4可知：砼已出现较大劣化，而钢筋锈蚀程度并不严重，即结构损伤情况主要由砼的材质劣化所引起。

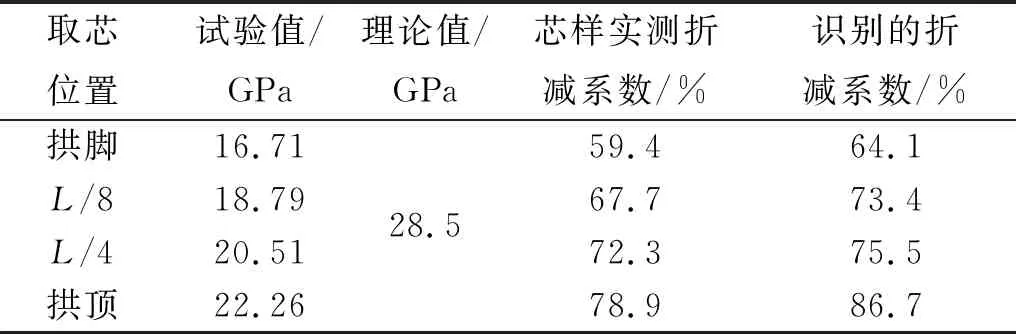
表3 砼芯样弹性模量试验值

表4 拱肋钢筋锈蚀电位差

对比表2～4中数据，可知损伤识别结果可信，也进一步验证了通过试验模态分析的动态方法提炼结构模态损伤指标的变化来检测监测对象的健康状态是可行的。

4 结论

(1) 结合结构振动分析理论与遗传算法，利用柔度曲率比对损伤位置敏感度高与遗传算法对损伤程度敏感度高的优点构建损伤识别计算方法可行，可为桥梁结构损伤识别研究提供新思路。

(2) 损伤位置可通过柔度矩阵的主对角元素柔度差值曲率的相对变化量确定，基于柔度曲率比的损伤识别方法具有计算简易、所需模态参数阶数少、误判概率小及定位准确的优点，可减少损伤程度计算量，提高识别过程的效率。

(3) 采用双向自适应变步长变异遗传算法计算结构中各损伤单元的刚度折减系数来反映结构损伤程度，其识别精度和效率高，能识别的损伤单元数多，可用于较大规模结构的损伤程度识别。

(4) 以既有旧桥的拱肋为研究对象，对文中损伤识别方法结果与外观检测发现的裂缝位置分布状况、静载试验反演的结构弯曲刚度结果、芯样的弹性模量试验结果和钢筋锈蚀程度测试结果进行对比分析，验证了文中损伤识别方法的可行性和合理性。

(5) 在数值模拟中，桥梁结构损伤识别的模态数据未考虑噪音的影响，下一步研究中值得关注。