基于改进BP神经网络的大坝安全监测预报模型
李 明
(河南省水利勘测设计研究有限公司 安徽分公司,合肥 230601)
0 引 言
建立合理有效的大坝安全预报模型,对掌握其性态变化、保证大坝安全运行都具有重要意义。目前,大坝安全监控通常采用统计模型、确定性模型和混合模型[1]。由于建立在观测误差的数学期望为零、呈正态发布、各次观测相互独立的统计学前提下,因此这类数学模型回归易失败、预报精度较低,无法满足实际工程要求。
人工神经网络兼具高度容错性、鲁棒性以及出色的非线性逼近性能,被广泛应用于回归拟合、聚类、模式分类、优化计算等众多领域。在大坝安全监控中,可考虑使用人工神经网络建立高精度监测预报模型。
1 BP神经网络的基本原理
BP神经网络,即采用误差反向传播算法的人工神经网络,由输入层、一个或多个隐含层以及一个输出层3部分组成[2]。见图1。
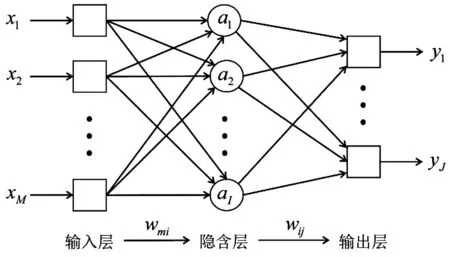
图1 3层BP神经网络的结构
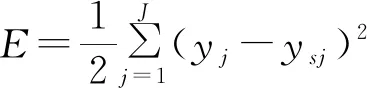
BP算法包括信息的正向传递过程和误差的逆向传播过程。
1) 信息的正向传递。公式如下:
隐含层第i个神经元的输出:
(1)
输出层第j个神经元的输出:
(2)
2) 误差的逆向传播。按照训练规则,连接权值与阈值的调整增量应与误差梯度成比例 ,即:
(3)
式中:η为学习率。
调整隐含层与输出层之间的权值wij和阈值b2j(即从第i个输入到第j个输出):
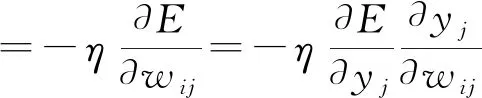
(4)
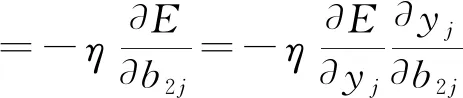
(5)
调整隐含层与输入层间权值wmi和阈值b1i(即从第m个输入到第i个输出):
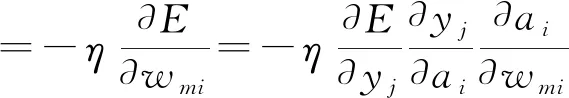
(6)
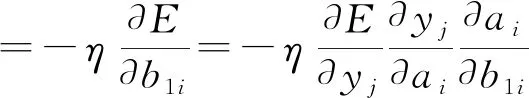
(7)
BP神经网络理论依据坚实,推导过程严谨,具有实现复杂非线性映射的能力,特别适合求解内部机制复杂的问题。但BP网络也具有一些难以克服的局限性:
1) 需设参数较多,且参数的选择并无有效方法。到目前为止,上述参数的选定尚无理论依据,只可通过经验给出粗略范围,致使算法稳定差。
2) 训练过程学习率敏感。若学习率太小,收敛可能很慢;若选得太大,又可能出现学习不稳定的现象。目前,学习率的选择缺乏简单有效的方法。
3) 易陷入局部最优。从根本上,BP算法是一种梯度最速下降算法,易出现局部极小值的问题,当位于局部极小值点时,就可能得出错误的结果。
4) 初始权值敏感。网络对初始权值的选取较为敏感,初始权值的改变将影响网络的收敛速度和精度。
5) 样本依赖性。当有新学习样本加入时,将会影响已学习过的样本。如果样本集合代表性差、矛盾样本多、存在冗余样本,网络就很难达到预期的性能。
2 改进的BP神经网络模型
针对BP算法的不足,本文进行以下改进:
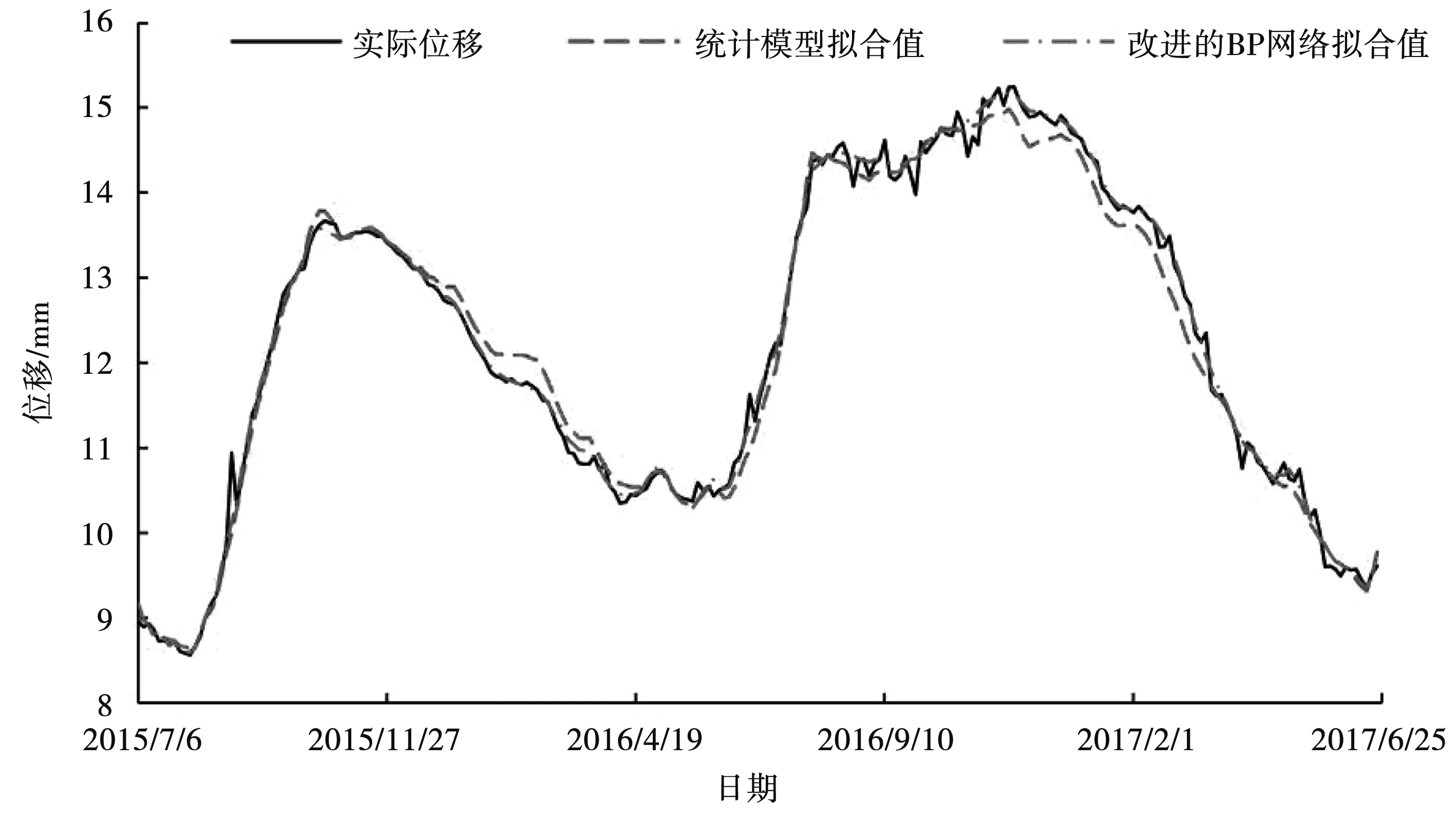
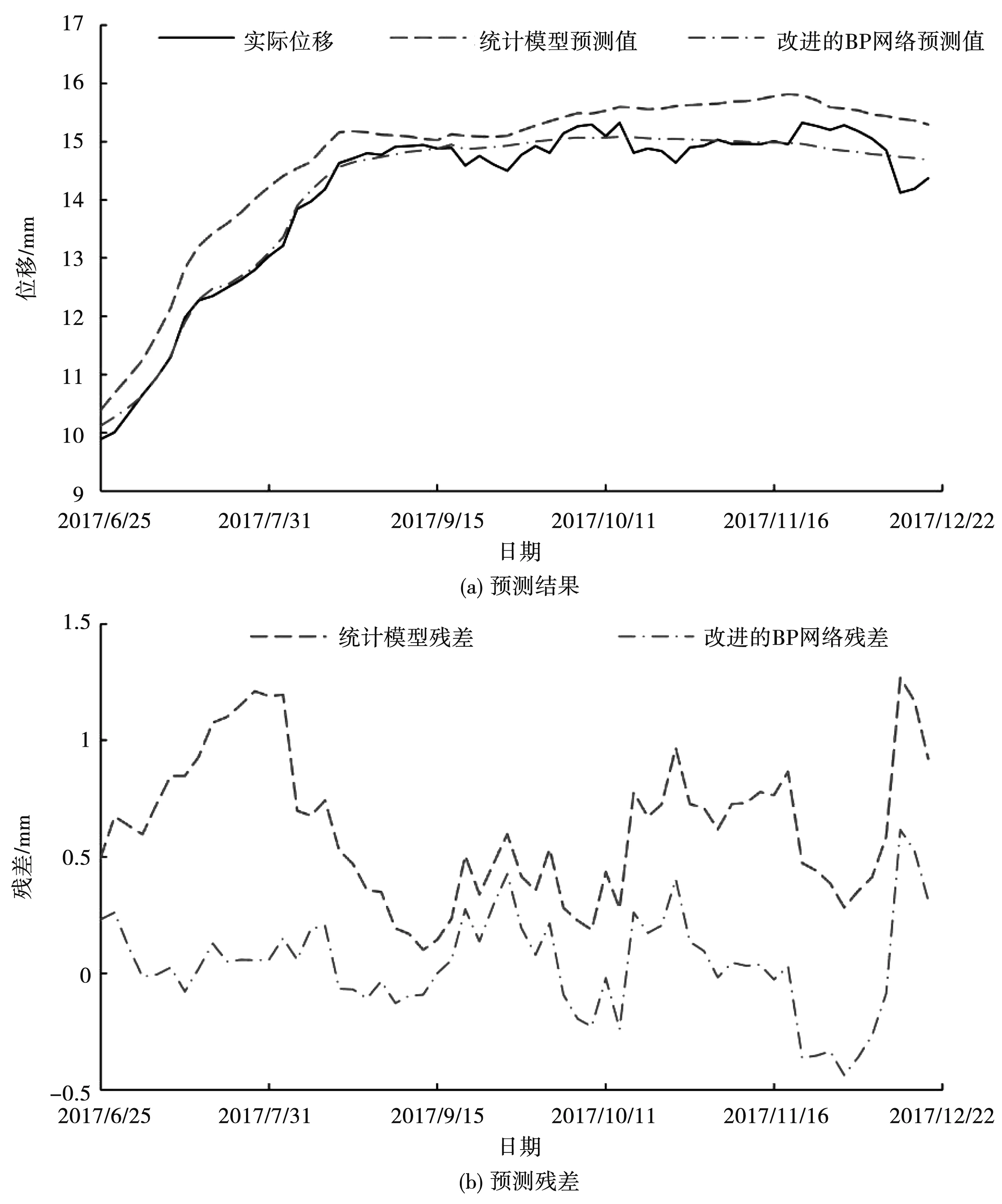
1) 采用特征选择算法精简模型输入变量,大幅降低网络结构的复杂度,有效提升模型的拟合和外延预测能力。对于包含n个样本、M个变量属性的输入变量系X={xi|xi∈RM,i=1,2,…,n}列,本文采用逐步回归的方法进行特征选择,设置信度a=0.1,通过式(8)进行输入变量的引入剔除:若Fp>Fain(1,n-k-1),则将变量xp引入模型,并对模型中已有变量重新进行显著性检验;若Fq (8) (9) (10) (11) 2) 引入增减量因子,构造可变学习率的网络学习算法。标准最速下降BP法中,学习率是一个不变常数,网络学习易过拟合。故需引入学习率增减量因子:当误差以减小的方式趋于目标时,修正方向正确,可以增加学习率,在原基础上乘以学习率增量因子;当误差增加超过一定范围时,说明前一步修正不正确,应减小步长,在原学习率基础上乘以学习率减量因子。 (12) 式中:kinc为学习率增量因子;kdec为学习率减量因子。 3) 引入动量因子,增加学习算法的稳定性。 (13) 式中:t为训练次数;η为学习速率;α(0<α<1)为附加动量因子;αΔw(t)为附加动量项。 取某混凝土拱坝15#坝段IP-01测点的径向位移监测数据为研究对象,建立基于改进BP神经网络的预测模型,同时构建对应的统计模型,进行对比分析。 根据安全监测原理[1],坝体位移主要受水压、温度和时效因素影响,可分解为: δ=δH+δT+δθ (14) 式中:δ为测点位移测值;δH、δT、δθ分别为水压分量、温度分量、时效分量。 该坝属于混凝土拱坝,在水压作用下产生的位移水压分量与大坝上游水深的1~4次方有关,选取上游水深作为水压分量的因子: (15) 考虑到该坝已经运行多年,选用时间周期项模拟坝体温度场的变化,具体形式为两组谐波因子: (16) 时效分量应能表征坝体随时间变化而产生的非线性位移,此处采用多项式附加对数时效因子: δθ=c1(θ-θ0)+c2(lnθ-lnθ0) (17) 式中:时效项模型输入量为(θ-θ0)、(lnθ-lnθ0)。 基于Matlab平台,编程实现上述改进BP神经网络算法。模型输入、结构和参数设置为: 1) 输入归一化。考虑到输入层的数据具有不同的量纲,宜对输入数据进行规范化处理,将输入样本限制在[0.1,0.9]之间,具体通过mapminmax函数实现。 2) 网络结构。本文选用的BP神经网络包含一个隐含层:输入层根据样本输入量的维数,节点数为9;隐含层结点数根据经验公式,经过多次试算,大致确定为18时训练过程收敛最快,效果最好;输出结果为位移监测量1项,确定输出层结点数为1。因此,该大坝变形预测模型的神经网络结构确定为9-18-1的形式。 3) 传递函数。隐含层使用Logsig,输出层使用Purelin函数。 4) 训练参数。训练方法采用学习率可变附加动量因子的BP算法,据此设定训练参数:最大训练次数1 000,学习率为0.01,目标误差为1e-5,噪声强度0.01,动量因子0.7,学习率增量因子1.05,学习率减量因子0.8。 5) 初始权值。初始权值选择极大影响着网络的学习速度和效果。初始权值过大或过小都会对性能产生影响,通常将初始权值定义为较小的非零随机值,经验值为(-2.4/F,2.4/F),其中F为权值输入端连接的神经元个数。由此初始权值可确定为(-0.3,0.3)。 确定完以上参数后,将归一化处理后的样本数据输入网络中进行训练,待网络收敛,即得到用于大坝变形预测的BP神经网络模型。 选取2015年7月6日至2017年12月19日共300组数据作为分析资料,其中前240组数据作为学习样本,后60组数据作为预测样本,各模型的拟合和预测结果见图2、图3,预测精度见表1。 建立的统计模型表达式: (18) 为验证改进BP神经网络的混凝土坝变形预测模型有效性,将均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)作为预测效果指标,与上述统计模型进行对比,获得各模型的拟合、预测结果见图2、图3,预测精度见表1。 图2 模型拟合结果 图3 模型预测结果 表1 模型预测精度 由图2可知,改进的BP网络模型拟合效果较好,拟合结果与实测值几乎重合;而统计模型结果与实测值前期基本重合,后期出现大范围的偏差。由图3所示预测结果可知,改进的BP网络模型充分发挥了非线性逼近能力,预测值与实测值贴合紧密,具体反映在残差过程线上就是残差在坐标零轴上下波动;统计模型预测结果与实测值偏差较大,已不能表征实际位移的变化趋势。从预测效果指标上看,较传统统计模型,改进BP网络模型的误差分别降低68.75%、75.17%和74.62%。由此,改进的BP网络模型较统计模型预测效果更好,精度更高;且能直观、准确反映出位移的变化趋势,在工程中具有实际意义,建立监控模型时可优先考虑选用。 1) 本文从逐步回归输入变量特征选择、可变学习率和附加动量因子学习算法等角度改进了BP神经网络模型,并将其用于大坝的变形预测中。结果表明,改进的BP网络模型拟合和预测精度值均要明显高于传统统计模型,且能直观、准确地反映位移变化趋势,在工程中具有实际意义;同时也证明了该法用于大坝变形监控中具有一定的实用性与可行性。 2) 为进一步提高BP神经网络的监测预报能力,可引入优化算法,作如下改进:为减弱早期数据对预测结果的影响,实现对观测资料的实时更新处理,可在BP神经网络误差计算和模型参数中分别引入遗忘因子,对数据影响权重进行动态调整[3];将BP神经网络与一些优化算法相结合,以实现算法特性的互补,如遗传-神经网络算法,利用BP网络的梯度下降算法,实现最快减少误差,利用遗传算法的群体搜索策略,避免过度依赖梯度信息,陷入局部最优[4]。
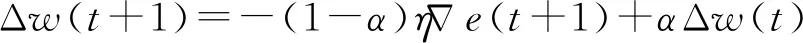
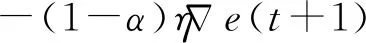
3 工程实例
3.1 模型输入量
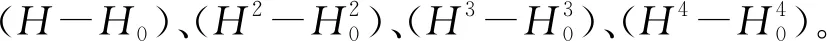
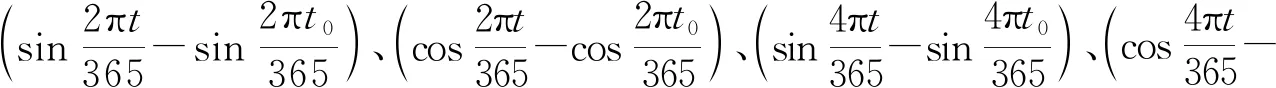
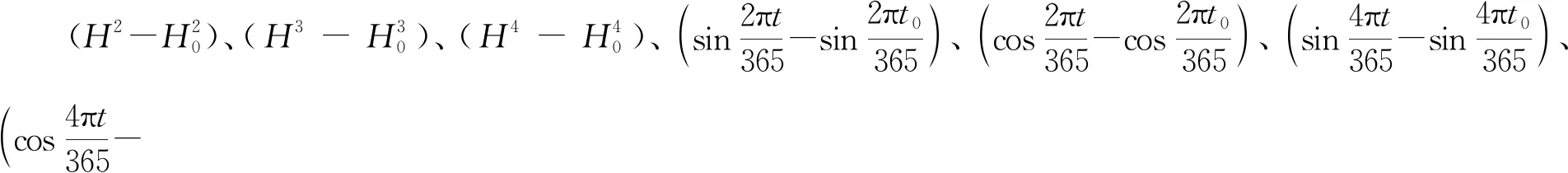
3.2 大坝变形预测模型的实现
3.3 结果分析
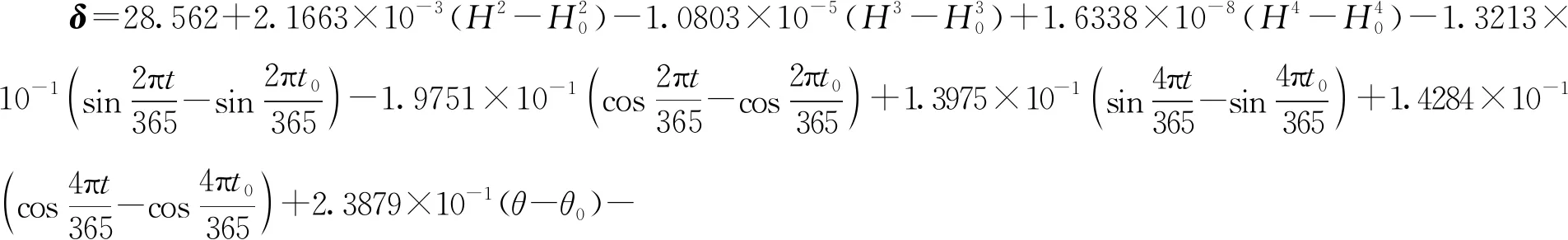

4 结 论

