基于遥感影像的近20年来黄河下游的河道演变

王 瑾

(河北工程大学 水利水电学院，河北 邯郸 056000)

0 引 言

河流系统属于一种复杂的系统，一般具有典型的自组织结构[1]。河流形态是河道特征的重要体现，与河流的环境变化和结构演变具有重要的关系。1970年代，Mandelbrot[2]出版了《分形：形态，偶然性和维数》，标志着分形理论的正式诞生。随着《自然界的分形几何》[3]的出版，标志着分形理论的进一步完善与成熟。因传统的方法难以揭示河流的长度和演变趋势[4]，“分维(Fractal Dimension，FD)”逐渐成为描述河流系统结构演变的重要工具[5]，目前已经逐步被应用于地貌学和河流统计学等众多学科[6]。利用长时间序列的河流分维变化表征河流的演化趋势，成为全球变化研究的热点之一[7]。

黄河下游一般指黄河河段中位于河南郑州桃花峪以下的部分[8]，合理地对黄河下游河道变化进行预测，对黄河下游的河道治理及水利工程的建设运用具有重要的意义。关于黄河下游河道分形分维的研究不多，赵云章[9]等在2005年对关于黄河的河床长度、河床弯曲度、河床浅滩等分形分维特征分别进行了研究。王卫红[10]等利用实测资料分析、理论判别以及分形维数计算等方法，分析了小浪底水库修建前后下游游荡性河段的河型演化过程。朱嘉伟[11]利用遥感(RS)与地理信息(GIS)技术的发展获取客观数据，分析得出黄河下游悬河河床地貌的分形分维研究特征，得出悬河段分维数值D的大小确实可以定量反映不同河段悬河的稳定性。所以，关于讨论黄河下游悬河的分形分维特征与河道演变具有重要的理论价值和实践意义。

1 河段概况与资料

1.1 河段概况

黄河下游高村以上河段是典型的游荡型河段，水流宽浅散乱，摆动频繁，河槽易淤积善冲，沙洲发育[12]。长约786 km，流域面积约2.3×104hm2，占黄河全流域面积的3%[8]。花园口断面是黄河中下游的节点水文站，其控制流域面积占黄河流域总面积的91.8%[13]。不同时期的黄河径流、泥沙含量都发生着不同的变化，全面了解河流水沙的时空分布及其变化过程，对黄河的综合治理具有重要的意义。

1.2 遥感影像数据

本文所用数据均来自于Landsat7系列的遥感影像，该系列卫星自1972年7月23号发射升空，已经积累了全球大部分区域的连续高分辨率遥感影像数据，为进行各类地球环境变化研究提供了数据[14]。本文选取1995-2016年间的若干幅基础数据，为方便进一步研究和数据处理，尽量选择云量较少的图片，都低于10%。为保证提取黄河水体的精准度，本文对影像进行辐射定标、大气校正、图像剪裁等预处理[15]。

1.3 数据处理

在遥感影像中，河道的边界线以及河中的滩地与周围水体的界限并不明显，提取难度较大。本文主要采用基于蓝光波段的归一化差异水体指数(NDWI)的方法，即：

NDWI=(B-NIR)/(B+NIR)

经过聚类、去除部分小斑块后，即可得到基本的黄河河道。为便于后续分析，结合目视解译方法，将研究区域的黄河河道单独剪裁出来。运用大津法将图像二值化处理，得到相应的黄河下游矢量图。

2 河道分维

分形原理：河流形态较为复杂，传统的方法难以揭示河流的长度特征及其演变趋势[16]。在20世纪60年代，Benoit Mandelbrot[17]提出分形几何学以来，分维(Fractal Dimension，FD)就成为描述河流系统结构演变的重要工具。

本试验采用的是河流分形中常用的计盒维数法，也被称为闵可夫斯基维数，最初是由Gangepain和Roques-Carmes[18]提出的一种计算图像盒子维的近似算法，后来Keller[19]等根据Voss的思想提出了一种改进方法，最后N.SarKar和B.B.Chaudhuri[20]在分析众多算法的基础上，提出一种较为简单的算法，即现在也被大多数人常用的盒子维计数法，其相比上述两种方法，更加简单、快速、精确，也被简称为DBC(Differential Box Counting)。

其基本原理为用长度为r的测量方格覆盖在河流上，然后统计出河流所通过的方格数目N(r)，可以简单概括为把这个分形放在一个均匀分割的网格上，数一数最小需要几个格子来覆盖这个分形。通过对网格的逐步精化，查看所需覆盖数目的变化，从而计算出计盒维数。具体计算公式如下:

N(r)∝r-FD

(1)

(2)

3 分维过程与计算结果

3.1 枯水季分维过程与结果

首先利用ENVI平台将4个时间断面下的黄河下游河道形状提取出来，从图1中可以看出来近20年黄河下游河道河形的变化并不是很明显，但是河宽是有明显的变化的，逐渐变窄。

图1 黄河下游河道演变

为分析黄河下游河道时空的具体变化情况，试验首先统计了1995-2016年间流量的情况，具体流量趋势见图2。按时间线以及数据的实际情况，较为均等地选择了1995、2003、2011、2016共4个年份的卫星图片，均集中在12月份及1月份等冬季枯水季节，为更好地分析河道分维的具体变化情况，下文也选取了丰水年的具体数据进行相应的分析。

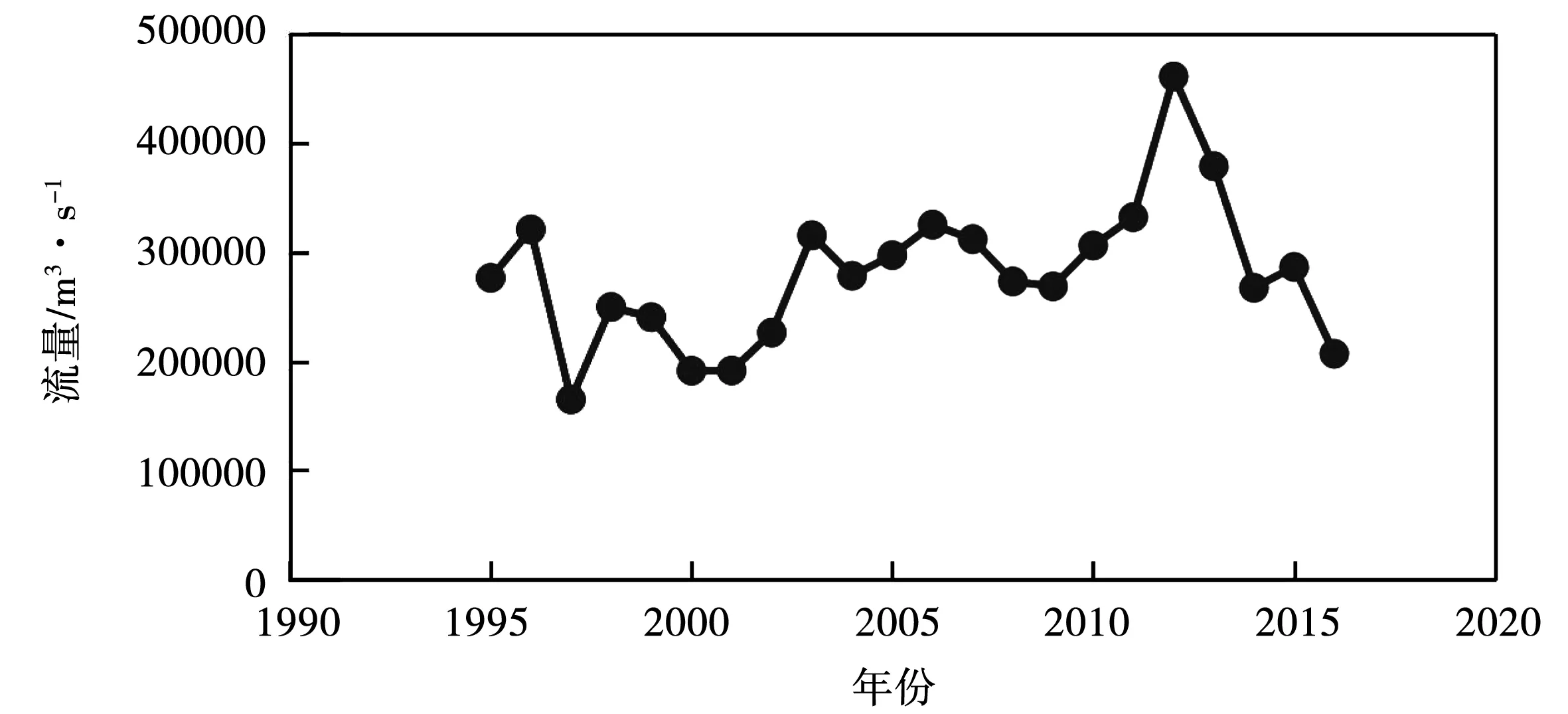
图2 近30年间黄河下游流量变化

根据上文所述公式计算出不同时间下的河道分维值，同时为保证试验的准确度，同样选取了不同年份的、同属于Landsat7系列的遥感图像，具体情况及统计结果见表1。

表1 枯水季黄河下游河道方格数目统计

根据以上数据，对河网所占的盒子数N(r)与尺度r两者的对数进行坐标系线性拟合，得到以上不同年份的分维数。各个时间断面下河流分维值的计算结果显示(图3)，近20年来分维值在1.454 5～1.552 3之间变动，平均值为1.507。并且各个方程的拟合度非常高，R2值均在0.99以上，这也说明黄河下游河道的分形特征显著。

图3 枯水季黄河下游河道lgN(r)与lgr散点图

通过以上4个时间断面黄河下游河道分维数值的分析，分维数值趋势的变化，可以得出从1995-2016年间这20年的时间段内，河流一直处于比较稳定的趋势之内。近10年来，黄河下游河道分维数值的变化趋势明显是一直下降的，从1.552 3下降至1.454 5，下降了0.1，虽然变化程度不算很大，但是可以说明黄河下游河道的整体游荡程度正在逐渐减弱，游荡型在向相对稳定型的方向缓慢发展。其原因可能是自1999年修建小浪底水库之后，由水库控制下泄特定的水沙，相比原来自然状态下的来水来沙状态规律了许多。

3.2 丰水季分维过程与结果

在2003年之前，黄河下游的大流量月份并不固定，大都分布在4、7、8、9、10月份，并且大流量之间的差距较大。但是在2003之后，下游的大流量大部分集中在6月份，也有少量在7月份，数据也相对稳定很多，波动周期相对以往更长了。

所以本试验主要选择2003、2006、2012共3个丰水年的数据，并且按上述步骤处理这3张卫星图片。为进行更好地对比以及研究的可行性，仍选择用21×3(长×高)共63个边长为9 600 m的正方形方格覆盖研究区域，然后根据上述公式计算出不同时间下的河流分维值，具体情况见表2和图4。

表2 丰水季黄河下游河道方格数目统计

图4 丰水季黄河下游河道lgN(r)与lgr散点图

从图4数据可以看到，其相关系数都在0.99以上，拟合性较好，即这段黄河下游分维数也具有一阶分维特性，其数值大都在1.55左右，并且数值较为稳定，并没有下降趋势，与上边枯水季明显的下降趋势相比可以看到，黄河丰水年的河道游荡性变化不大。同时，从大流量的分维数值也可以看出，每年大流量的洪水对河道的冲刷是较为明显的，在每年这种持续的冲刷之下，河道裁弯取直的可能性很大，同时也说明在人类活动的干预下，对黄河下游的影响是比较显著的。

河流长度的分维数大小反映了河流的弯曲程度，分维数越大，表示河流越趋于摆动；分维数值越小，表明河流趋于稳定。由此可见，在分析河道的稳定性上，枯水季的河道分维值比丰水季的河道分维值更加具有分析与参考价值。

4 主要结论

通过近20年来黄河下游河道的遥感影像资料，利用ENVI及Arcgis等平台分析不同时间断面下的黄河下游河道整体情况，并分析黄河下游河道近20年变化的主要原因，主要得出以下结论：

1) 黄河下游河道具有明显的分形特征，不同时间断面的拟合优度R2>0.99，河道分维数值均在1.552 3～1.454 5之间变动。

2) 黄河下游河道的分维数值整体呈现下降趋势。相比丰水季，枯水季的河道分维数值更能反映黄河下游河道变化的具体情况，丰水季河道的分维数值普遍较高，不利于观察河道历年变化规律。

3) 每年大量流量过后，分维数值在不断减小。虽然减小程度很微小，但如果长时间的积累，很有可能在人工的干预与控制下，黄河下游河道会逐渐由游荡河道向顺直化河道转变。