“点”视阈下学生空间“动态想象”能力的培养
殷法泉


【摘 要】学生空间观念的培养一直是数学教学的一个难点,原因之一就是很多的几何知识点都成为“静点”,缺乏“动态挖掘”,从而“点—线—面—体”没有实现真正的联动。本文以“三角形的复习”为例,立足于学生“动态想象”能力的培养。通过“写—画—算”三个维度的创新,从“点”的角度,在动态视觉上另谋思“路”,从而连“点”结“网”构“体”,给学生架构一个序列的、完整的“几何框架”,为学生空间观念的丰盈提供保障。
【关键词】“点” 动态想象 空间观念
《三角形的认识》是人教版数学四年级下册的学习内容,六年级学生对三角形的各个知识点已了然于胸。但我们发现,这些知识点在学生的记忆里都是独立存在的,学生并没有将知识点有效地串联起来。有的虽有涉及它们间的联系,但只是点到为止,更没有延伸、融合。课堂教学现状告诉我们,很多的几何知识点“安静地躺在那里”,缺乏“动态挖掘”,“点—线—面—体”未有真正的联动,我们的空间知识教学效果收效甚微。因此,真正培养学生空间观念需要我们拓宽思维,另辟蹊径,让静态的几何点“动起来”,让学生的空间观念丰盈起来。本文以“三角形的复习”为例,在几何知识点的动态想象上另谋“思路”,通过“写、画、算”三个维度的拓新,从“点”的角度,从动态的、综合的视角进一步丰富与充实学生对各类三角形特征的理解与掌握,打通三角形之间的关系,形成新思维、新方法,努力提升学生的数学学习力。
一、动态想象,以“点”带“面”,写出“真相”
学生从接触数学的那刻起就好像被数学这门学科套了个“圈子”——数学学习只要会用演算解决问题就成功了。然而,教学中我们时常会发现一种奇怪的现象:很多学生纸笔练习没问题,但如果需要用语言将自己的想法清楚地表述出来时就噤口不言了。学生数学素养的提高不能仅仅局限于学生会解题,也要注重学生表达自己数学观点能力的提高。“图形与几何”这种空间领域的学习本身就抽象,“空洞”的讲解很难让每一个学生理解。此时,就需要我们把静态的几何知识点借助图示动态地呈现出来,更要让学生学会正确地“全盘托出”。
如在“三角形的复习”中,我们可以通过下题引入:
下面方格图中有两点A、B(如图1),现需找一个点C,使它和另外两点可以构成一个三角形。那么点C需满足什么条件就一定能和A、B构成三角形?( )
给出两点,通过第三点的运动变化,让学生进一步感知三角形,体验图形之间的变换,让独立的知识点连成片、结成网,从而突破传统“线段”的角度,进而从“点”的角度加深学生对三角形三边关系“两边之和大于第三边”的理解。学生可以找到无数个变化着、运动着的点C(包括方格线上的和方格内的,而方格内的点往往是学生忽视的点)和A、B两点构成三角形,这无数个运动的点可以构成一个面,以“点”带“面”。我们不需要学生找出每一个这些具体的点,我们需要的是学生经历这种“由点及面”的全方位的思维碰撞。通过这些具体点C的动态变化,让学生从点的动态变化中感悟三角形成立时“点对边”的影响,重在让学生提炼出并会用语言有条理地表述出点C位置满足的充分不必要条件(只要A、B、C不在同一条直线上)。我们结合图可以显而易见地發现当点C与A、B在同一条直线上时三点是不能构成三角形的,此时三点连一线,更好地阐释了为什么“两边之和等于第三边时不能构成三角形”的原因。
二、动态想象,“点”出内通,画出“乾坤”
从“点”的角度“笼统”地巩固了构成三角形的三边关系后,我们需要从“按角分”和“按边分”两个标准从“点”的角度对已构成的三角形类别有更好的说明,进一步通过动态展示确定每类三角形点C的位置。我们可以进行如下设计:
点C和A、B可以构成各种三角形:
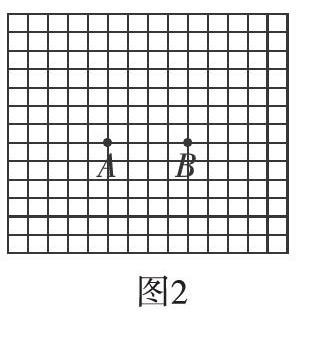
①若要构成直角三角形,那么点C的位置可以在哪里?请你在图2中画出;
②若要构成锐角三角形,那么点C的位置可以在哪里?请你在图2中画出;
③若要构成钝角三角形,那么点C的位置可以在哪里?请你在图2中画出;
④若要构成等腰三角形,那么点C的位置可以在哪里?请你在图2中画出;
⑤若要构成等边三角形,那么点C的位置可以在哪里?请你在图2中画出。
本题让学生初步感受 “点的运动轨迹与图形的关系”,由点及线、由线到面,把一个个独立的、静态的点动态呈现,点、线、面互通,也进一步沟通了三角形与其他平面图形的另一层关系,如图3中点C要和A、B两点构成直角三角形,点C的运动轨迹除了左右两条线(除去A、B两点)外,以AB为直径的圆(除去A、B两点)更好地阐释了三角形与圆的关系,也为后续学习“在圆中,直径所对的圆周角是直角”做好铺垫。
再则,通过动态演示、画一画,让学生深刻体验各类三角形的关系。如问题①、②、③的画图结果就是要让学生从另一个视角(脱离常用的集合图)认识直角三角形、锐角三角形、钝角三角形的并列关系,一个平面分成三块区域,形象、直观地阐释了它们的并列关系;问题④中点C的运动轨迹一部分是以A或B为圆心、AB为半径的左右两个圆(除去A、B、M、N四点),将圆半径知识综合运用到解决三角形的问题中来,体现知识的融合。问题④、⑤的答案很清楚地展示了等腰三角形与等边三角形的包含关系,向学生动态呈现“等边三角形为什么是特殊的等腰三角形”的原因——只有点C运动到X、Y两个特殊位置时等腰三角形才成了等边三角形。
“图形与几何”领域本身要求教学中要将几何的几个基本要素“点—线—面—体”循序渐进,有机整合,赋予学生完整的“几何概念体”。我们很好地利用“点的运动—线的勾勒—面的描述”这一规律,根据点的动态变化,利用旧知对“后知”进行预测、判断,让学生提前“后知后觉”,感悟数学知识内在联系的奥秘,体验探索、推理、分析的成功。
三、动态想象,由“内”及“外”,算出“玄机”
“点”,作为三角形的基本要素之一,它的运动可以改变三角形的形状。而有时另一种“点”,绕着三角形边运动的“点”,可以打开对三角形的另一基本要素“角”探索的新范畴。学生已经熟知包括三角形在内的各种多边形的内角和,在此基础上我们需要给予学生充分的探索空间,让学生经历“猜想—推理—验证”的全过程,探索多边形的外角和。因此,我们可以这样设计:
一只小瓢虫沿着下面这个三角形ABC(图5)的各边沿爬行一周,身体一共旋转了( )度。
对于学生来说,“三角形的外角”是一个新概念,所以先让学生根据图5猜想、描绘三角形的外角在哪里、三角形的外角应该是怎样的,进而去研究三角形的外角和是多少度、如何推算等。在此,我们借助小瓢虫的运动轨迹,把小瓢虫看作一个“运动的点”,动态演示,让学生找出外角。如图6中,小瓢虫沿三角形ABC的三条边爬行一周所转过的角是∠1、∠2、∠3,就是三角形ABC的三个外角,运用三角形的内角和知识,推算三角形外角和的度数,让学生充分享受外角和推算的过程,并以此为“原点”,给学生一个更广阔的想象空间:任意一个多边形(包括四边形、五边形、六边形……)外角和都是这个度数吗?让学生充分猜想、验证这些多边形外角和的计算规律,最终得出规律:多边形的外角和总是360°。
“三角形的复习”作为平面图形综合复习中的重要一环,我们必须立足于学生“动态想象”能力的培养,真正激活“图形与几何”领域每一个静态的点,让每一个“静点”动起来、变起来,将各个几何知识点在横向的广度和纵向的深度上都得到延伸、拓展,厘清各个几何知识点在整个数学学习阶段的来龙去脉,从而连“点”结“网”,给学生架构一个序列的、完整的“几何框架”,为学生空间观念的丰盈提供保障,也为我们整个“图形与几何”领域的“动态教学”提供借鉴。

