大跨度拱桥吊杆索力的测试研究
林天然
(浙江省交通规划设计研究院有限公司,浙江 杭州310000)
1 吊杆索力测试方法
目前吊杆索力测量的方法主要有千斤顶油压表法、压力传感器法、频率法和磁通量法等[1-2]。
(1)油压千斤顶法。吊杆在施工过程中通常使用液压千斤顶张拉。利用千斤顶油压面积一定时,油缸中的液压与千斤顶的张拉力成比例这一原理,可将油压表读数换算成千斤顶的张拉力。该方法的优点是比较直观,不需增加其他仪器设备,且有较好的精度,是施工过程中常用的索力测试方法。但这种方法仅适用于施工中正在张拉的拉索索力测量,对于己张拉完毕的拉索,无法使用这种方法测试索力。
(2)压力传感器法。吊杆在张拉时,千斤顶的张拉力通过连接杆传递到锚具上,运用电阻应变片测量的原理,制作压力传感器,套在连接杆上。将压力传感器放在锚具和锚垫板之间,便可对索力进行长期监测。常用的压力传感器主要有振弦式压力传感器、压电式压力传感器、电阻式压力传感器、光纤光栅式压力传感器等。但压力传感器价格高、质量大,而且压力传感器的输出结果存在较大误差,长期监测稳定性差,使其在结构长期监测中的效果不佳。
(3)频率法。频率法主要借鉴斜拉桥索力测试中普遍采用的弦振动公式,即借助振动信号理论,从动力平衡微分方程入手,导出吊杆索力与吊杆自振频率之间的关系,即通过检测吊杆的自振频率来得出吊杆索力。在测试时,该法并不需要预埋传感器,而是利用环境随机激励或人工激振作为激振源,在吊杆上附着高灵敏度的传感器,拾取吊杆在环境激励下的振动信号,经过滤波、放大、谱分析,测得吊杆的自振频率,然后根据自振频率与索力的关系确定索力。频率法测试索力具有操作简单、费用低、测试效率高和精度相对较高等优点。只要准确建立索力和频率的关系,利用频率法测索力便可达到较高的精度。
(4)磁通量法。磁通量法最先由国外提出,是一种比较新的索力测试方法。其原理是利用小型电磁传感器,测定磁通量变化,再根据应力、温度与磁通量变化的关系来推算索力。目前磁弹索力传感器的研究主要有:捷克斯洛伐克Dynamag 公司研发的磁弹传感器,已应用于江苏江阴大桥;美国芝加哥伊利诺依大学的Wang 与柳州欧维姆机械有限公司联合研制的CCT54G 和CCTl35J 磁通量传感器,已应用于天津永和大桥。虽然磁弹索力传感器已经应用于实际工程的索力测量中,但是其中的许多关键问题仍需解决和完善,如磁弹索力传感器系统的精细建模与系统优化,实验研究的完善,信号抗干扰能力和测量精度的提高等。
目前,由于用频率法测索力的仪器便于携带、测量方便、可重复使用且测量精度能满足工程实践要求,故在实际工程中使用最多,本文对其进行分析。
2 频率法测索力的基本原理
索线形解析理论的基本假定如下:
(1)吊杆在面内振动和面外摆振不具有耦合性,可以看成平面问题来研究。
(2)振动引起的挠度远小于吊杆的静载挠度。
基于上述假定,对吊杆建立如图1 所示的振动模型。图1 中:x为沿吊杆轴向的坐标;y为吊杆的振幅;T为吊杆的索力;l为吊杆的计算长度。
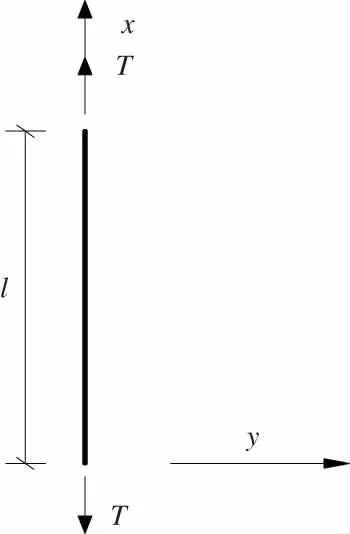
图1 吊杆振动模型
应用结构动力学原理建立吊杆的振动微分方程[3]:
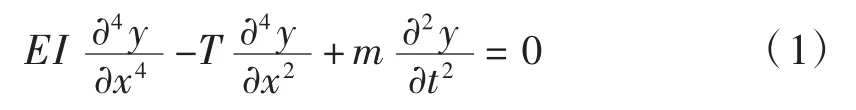
式中:EI为吊杆的弯曲刚度;m为吊杆的单位长度质量,kg/m;t为时间。式中第1 项体现了抗弯刚度对吊杆振动的影响。令:
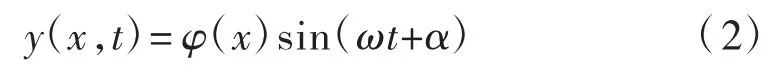
式中:φ(x)为吊杆的振型函数;ω 为吊杆的固有振动角频率;α 为吊杆振动的相位角。
将式(2)代入到式(1)中,可以建立吊杆索力与其振动频率之间的关系,即:
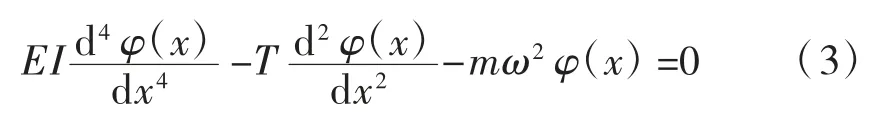
将吊杆看成两端张紧的弦即两端铰接,则吊杆自由振动的振型函数为:

边界条件为:φ|x=0=0,φ"|x=0=0,φ|x=l=0,φ"|x=l=0。
根据弦振动理论,可得吊杆索力T与振动频率fn之间的关系为:
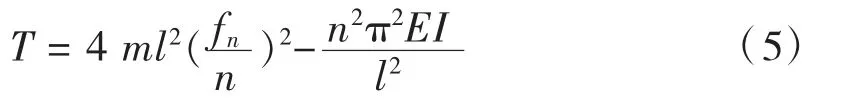
式中:n为吊杆自振频率的阶数;fn为吊杆的第n阶自振频率。
测试时只需要测出吊杆的频率和对应的阶数,代入式(5)中即可得到吊杆的索力。式(5)右端第2项为考虑结构抗弯刚度的影响。大量实践及研究[4]表明:当吊杆的长度小于5 m 时,如果不考虑抗弯刚度的影响会使测得的索力产生较大的误差,但当吊杆长度大于5 m 时,可以忽略抗弯刚度的影响。振动阶数n一般取1,此时式(5)变为:

3 基于修正吊杆计算长度的索力测试研究
虽然用频率法测索力在实际工程中运用最广,然而单纯地运用弦理论进行系杆拱桥吊杆索力的测试会存在一些误差,主要是由于:(1)未能准确考虑抗弯刚度对索力测量的影响;(2)两端铰支的边界条件并不适合所有结构;(3)吊杆计算长度对索力测量影响较大,尤其是对于拱桥上的短索。但是要计入抗弯刚度对索力测试结果的影响并不容易。虽然不同系杆拱桥其吊杆两端的边界条件有可能不同,但由于测量索力的索力仪采用的原理就是弦理论即两端铰接的形式,并且不考虑结构抗弯刚度的影响,且实践证明吊杆的计算长度对索力测量的精度影响很大,基于简单方便及可行性考虑,本文统一用一个吊杆计算长度的修正值进行修正计算。
大量实践和刘文峰等[5]研究表明,吊杆固有频率的测量误差可以控制在0.01%左右。由式(6)可知,对索力测量精度的影响主要体现在吊杆计算长度的精确确定上。由于油压千斤顶的读数比较准确,故在油压千斤顶张拉吊杆时即持油状态下拾取吊杆的固有频率,同时记录油压千斤顶的读数,此时用式(6)反算出计算索长l0,此l0即为修正后的吊杆计算长度。本文以某大跨度拱桥为例,对拆除主梁支架即体系转换之后、二期铺装之前的吊杆计算长度进行了修正,如表1 所示。
索导管及减振器只在系梁各个吊杆处安装,减振器到锚固端的距离为2.35 m。由表1 可见,两锚固点间的长度l与吊杆修正长度l0的差值在2.032 m 到2.537 m 之间,即其大约为减振器到锚固端距离的0.9倍到1.1 倍之间。修正前后索力的对比情况见表2。
由表2 可以看出,吊杆计算长度没有经过修正时,实测索力与理论索力相差很大,而吊杆计算长度经过修正后,实测索力与理论索力比较吻合,最小只相差1.14%;最大相差11.53%,位于拱脚,这是由于索较短且刚度较大造成的。由此可见,用频率法测索力的各种误差分析中,统一考虑一个吊杆计算长度的修正值进行分析具有可行性且简单方便,且长度修正值为减振器到锚固端距离的0.9 倍至1.1 倍之间。
4 结 语
(1)主要介绍了目前测试拱桥吊杆索力的几种方法及频率法测索力的基本原理。
(2)基于目前用频率法测索力的索力仪中都采用弦理论即两端为铰接的边界条件,且又不考虑抗弯刚度的影响,本文以某大跨度拱桥为例,提出了一个统一考虑吊杆计算长度修正值的方法进行分析。该方法具有可行性且简单方便,且吊杆计算长度的修正值为减振器到锚固端距离的0.9 倍至1.1 倍之间。
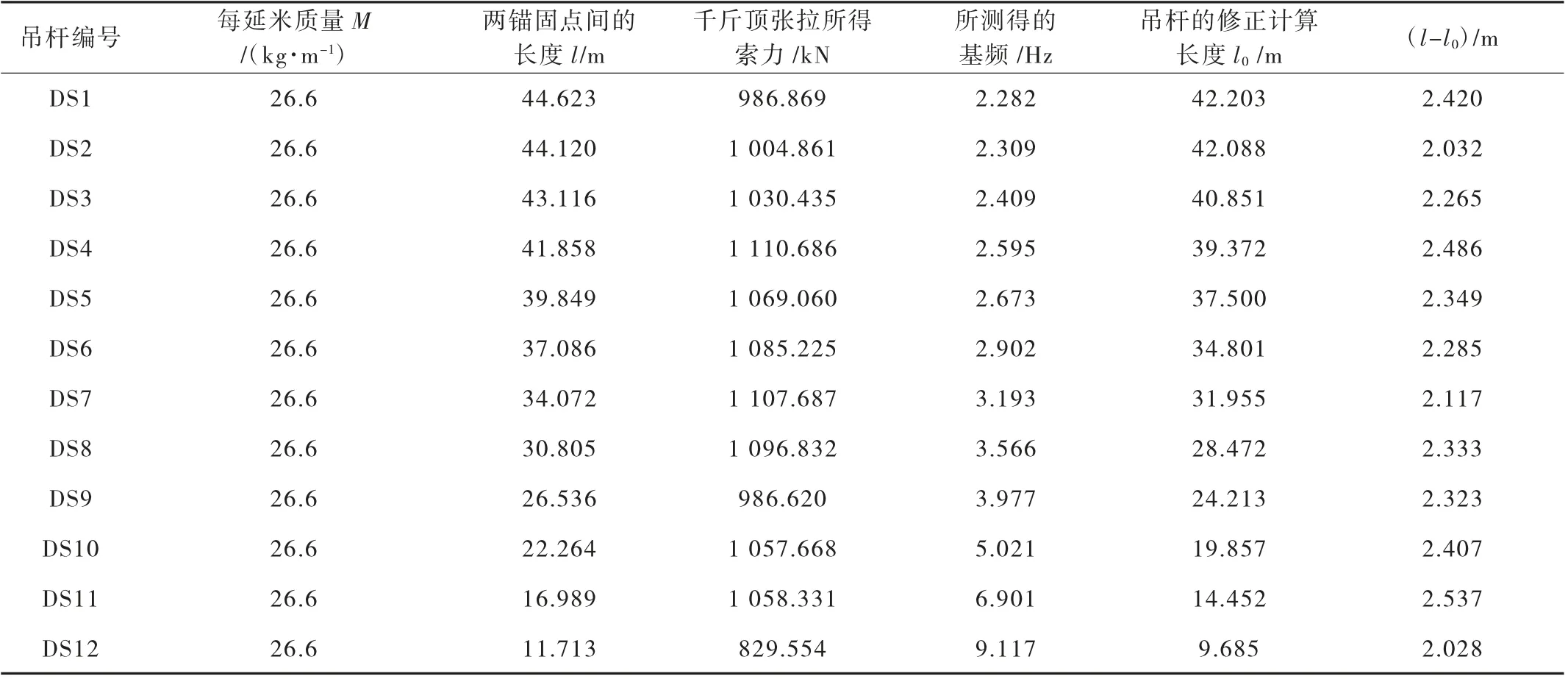
表1 吊杆计算长度的确定
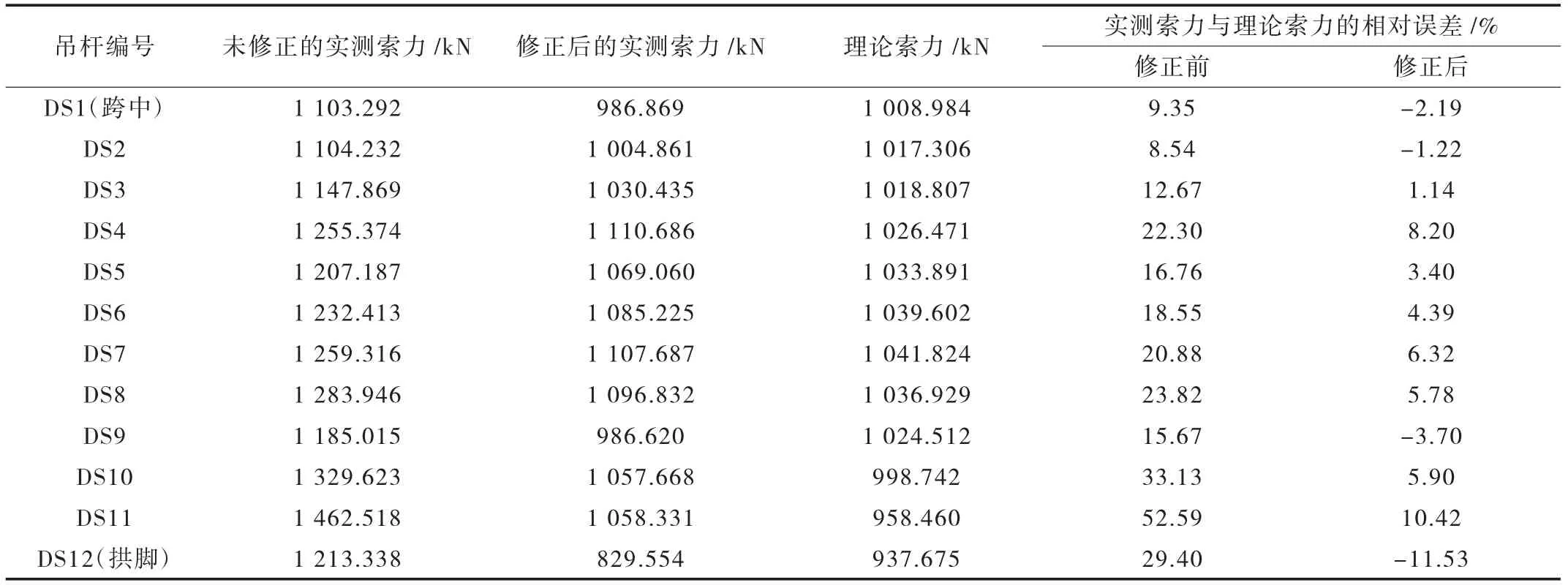
表2 修正前后索力与理论索力对比

