永磁同步电机无位置传感器启动策略的改进
张俊喜 张永雷
(青岛海信日立空调系统有限公司 青岛 266510)
引言
近年来,由于永磁同步电机(Permanent Magnet Synchronous Motor-PMSM)的效率高,动态特性好等优点,在家用电器,工业控制及汽车等领域被大量使用。
PMSM控制系统需要获得准确的电机转子位置信息。而在PMSM上安装位置传感器方法复杂,成本高,且在一些应用场合很难实现。由此,无位置传感器算法被提出来估算PMSM的转子位置。其中滑模观测器以算法简单,鲁棒性强等特点被广泛应用[1]。但在零速及低速情况下估算精度很低,不适用于电机的零速与低速工况,不能用于电机的启动[2]。针对此问题,有学者提出先对电机进行开环启动加速,使观测器估算精度可以满足要求时再切入闭环控制[3,4]。即三段式启动方法,分为转子定位、开环同步启动加速和闭环运行三个阶段。在定位和开环同步启动加速阶段中,电机反电动势较小,通过信噪比较低的电流检测及观测器计算的位置信息不准确,电机控制稳定性差[5]。因此,开环启动到闭环的切换至关重要,通常的方法是按照一定斜率减小电机电流,但这样易使电流脉动而造成失步。为克服此缺点,本文提出一种新的基于K/ cos2曲线减小电机电流实现平滑状态切换的启动方法。
1 PMSM转子位置的滑模观测算法
PMSM在两相静止坐标轴下的电机模型如图1。
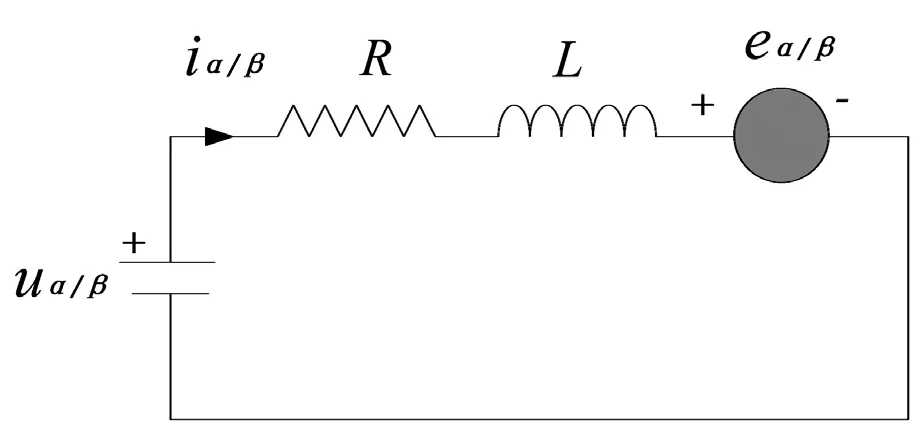
图1 电机模型
由图1可得PMSM的数学模型如式(1)。
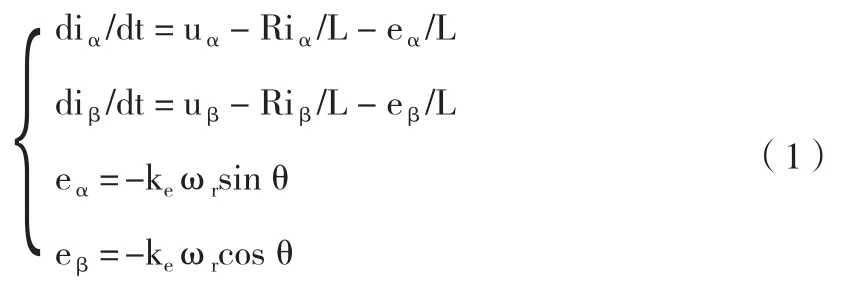
式中:
uα—两相静止坐标轴下α轴的定子电压;
uβ—两相静止坐标轴下β轴的定子电压;
iα—两相静止坐标轴下α轴的定子电流;
iβ—两相静止坐标轴下β轴的定子电流;
eα—两相静止坐标轴下α轴的反电动势;
eβ—两相静止坐标轴下β轴的反电动势;
R—定子相电阻;
L—定子相电感;
Ke—反电动势常数;
ωr—转子速度;
θ—转子位置。
根据滑模控制理论,由式(1)设计的滑模电流观测器如式(2)所示。
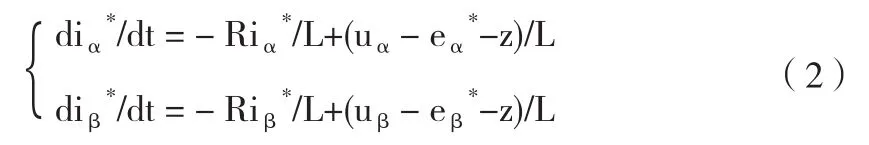
式中:
z—输出校正因子。
iα*—两相静止坐标轴下α轴的定子电流估算值;
iβ*—两相静止坐标轴下β轴的定子电流估算值;
eα*—两相静止坐标轴下α轴的反电动势估算值;
eβ*—两相静止坐标轴下β轴的反电动势估算值。
滑模面S定义如式(3)。

可得校正因子

式中:
Kslide—滑模系数,且大于零;
sign(S)—符号函数,S>0时,sign(S)=1;
S<0时,sign(S)=-1。
校正因子z被加到电压数学模型中来不断补偿电机模型,直到S=0。之后,可以通过z来估算反电动势eα、eβ。由于z的开关切换引起干扰,因此,需引入一阶低通滤波器进行滤波。反电动势观测模型如图2。
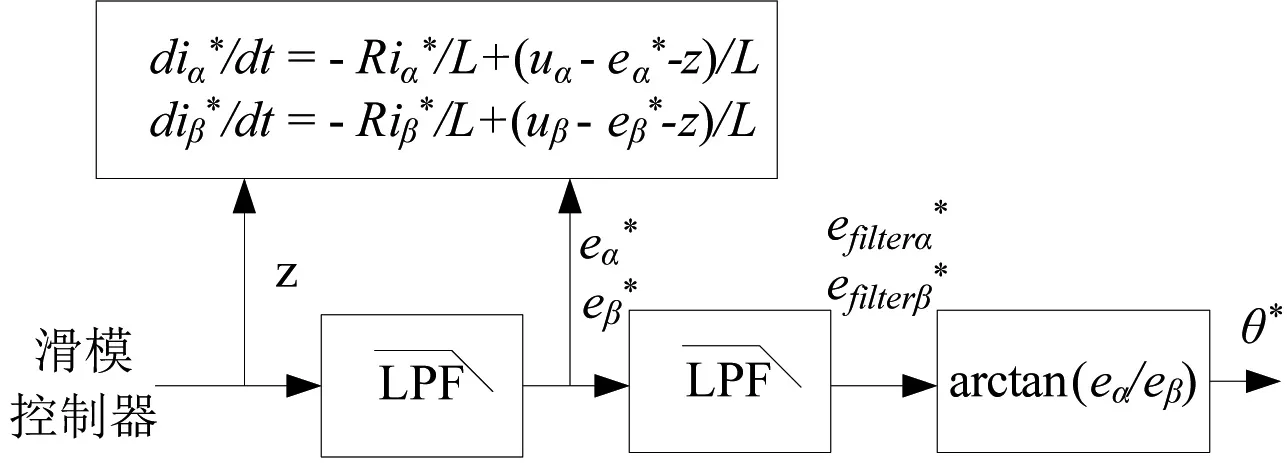
图2 反电动势观测模型
由于引入低通滤波器,会产生相位延迟,需要对估算角度θ*进行补偿。补偿角度可通过式(5)得到。

式中:
ωc—低通滤波器的截止频率。
最终,补偿后的估算角度如式(6)。

2 改进型PMSM启动方法
由于基于滑模的无位置传感器算法在低速时估算误差较大,因此不能直接启动PMSM,需采用其他启动方法,如I-F启动,即三段式启动策略。
2.1 I-F启动
定位阶段如图3所示,在定位前转子位置随机,给定旋转坐标系d*、q*轴与实际旋转坐标系d、q轴存在角度差θerr。定位时,施加一个定常的直流电流矢量iq*使电机转子被拖到指定的位置—q*轴进行启动,而此时保持id*=0。在定转子磁场的作用下,转子就能够定位到超前d*、q*轴90°的位置,d轴与q*轴重合。
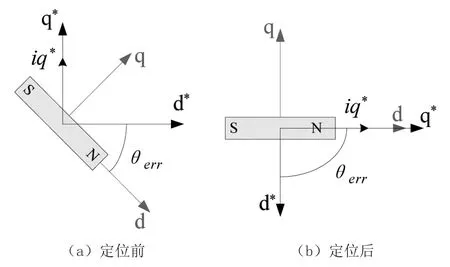
图3 定位过程
启动加速阶段,保持id*=0,iq*为常量并按照设定的位置角从定位位置开始加速旋转,则iq*在q轴的分量与d轴磁场产生的电磁转矩拖动电机转子按相同方向加速旋转。电磁转矩小于负载转矩时,电机转子会滞后,θerr变小,则iq*在q轴分量增大,电磁转矩增大,电机会加速到新的平衡点,反之,调整过程相似。这就是I-F控制的自平衡特性。
2.2 状态切换过程
滑模观测器在电机转速较高时才可以准确估算出电机转子位置,因此需要在电机加速到某个转速时才可以切换为闭环。但同步启动中的转子位置为给定角度,而滑模观测器为估算的实际角度,两者之前存在角度偏差θerr,这样直接切换,电流相位会出现跳变,导致失步或电流过冲等故障。
因此,需要采用适当的过渡方法来实现平滑切换。文献[6]提出一种切换方法:按照固定斜率减小q*轴给定电流iq*使θerr趋向于零,当θerr小于设定的阈值时进行状态切换。根据I-F控制的自平衡特性,可以通过减小给定q*轴电流的方式减小其在q轴分量,使电磁转矩减小,进而减小角度差θerr,当角度差θerr足够小时再进行闭环切换,电流相位变化较小,切换成功率提高。此种方法iq*的设置对角度差θerr影响较大,为了实现平滑切换,要设置较小的电流减小斜率,需要较长的电流调节过程,实用性不强;而为了缩短调节时间,则设置较大的斜率来减小电流,而实际电机机械系统反应落后于电流变化,切换时容易出现电流扰动,并且θerr一旦变成负值,电机会有失步风险。
2.3 改进的状态切换方法
为解决上述通过固定斜率调节iq*进行状态切换所产生的问题,本文提出一种根据K/ cos2曲线逐渐减小iq*的过渡方法,在过渡过程初期,iq*减小较快,进而快速减小θerr,当θerr变得较小时,iq*减小速度放慢,使电机机械系统能够跟上电流变化,θerr减小到接近零的设定阈值时切换到滑模观测器的闭环控制,实现平滑过渡。本文提出的改进的切换方法如式(7)。

式中:
K1—调节系数;
φ—调节角度;从初始设定角度开始递减。
K1、φ均为了调节iq*过渡变化曲线设置。
3 实验
本实验选取瑞萨的R5F562T7ADFP作为主控CPU,主频为100 MHz,PWM载波周期设置为6 kHz。实验所采用制冷压缩机用永磁同步电机参数如表1所示。
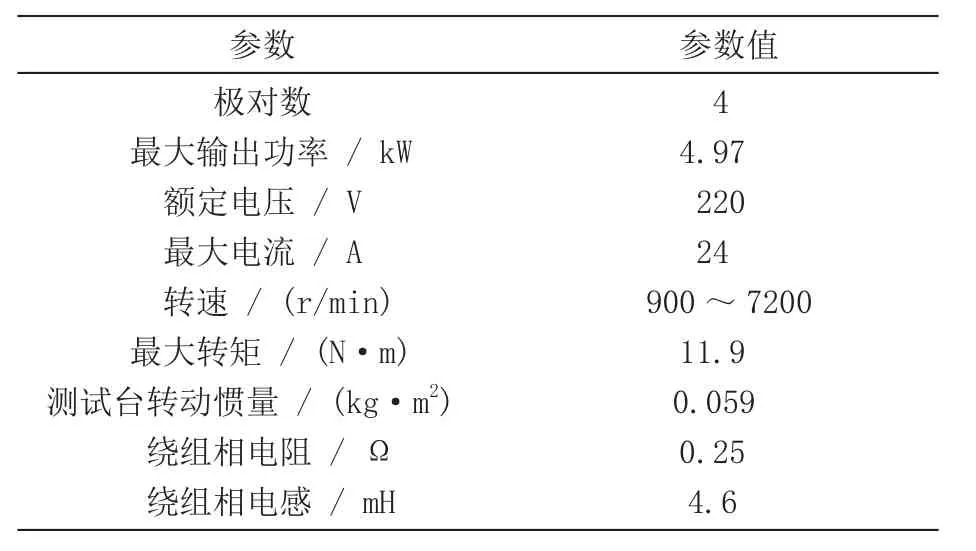
表1 试验用永磁同步电机参数
I-F启动过程设定:定位阶段2 s,启动加速阶段5 s,启动电流21 A peak;过渡过程开始转速为600 rpm,最终目标转速1 200 rpm;切换角度差阈值1度。
图4为按照固定斜率减小iq*的方法下采集的q轴电流、角度差θerr、转速n和相电流iA波形。
从图4可以看出,按照固定斜率控制iq*减小的过渡方法,切换时会出现电流扰动,如图4(a)的iq电流,图4(d)的相电流,转速在加速到600 rpm进入过渡过程时出现减速现象,如图4(c)。图4(b)角度差在启动加速阶段出现的波动是由于负载转动惯量较大,扭矩波动引起的,属正常现象。
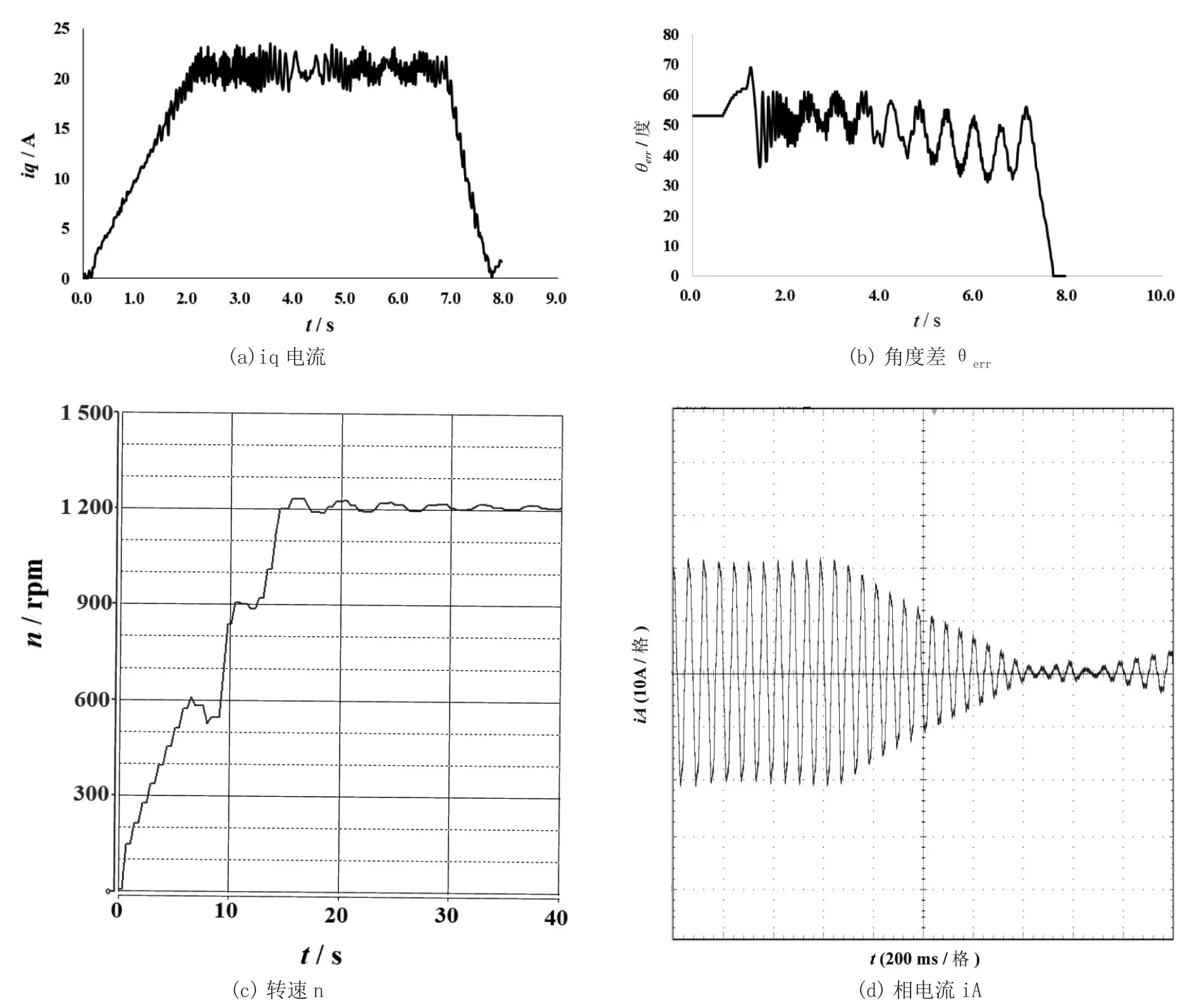
图4 固定斜率控制波形
图5为按照式(7)所示曲线减小iq*的方法下采集的q轴电流、角度差θerr、转速n和相电流iA波形。这里式(7)中K1设定为0.633,φ初始设定为80度,每周期以0.2 度递减。
从图5可以看出,采用K/ cos2曲线控制iq*减小的过渡方法,切换过程较为平滑,转速和电流均没有出现波动,由于此方法在过渡阶段后期电流减小速度趋缓,使得机械系统可以赶上电流变化,电流不必减小到很小就可以使角度差θerr减小到接近零的阈值。
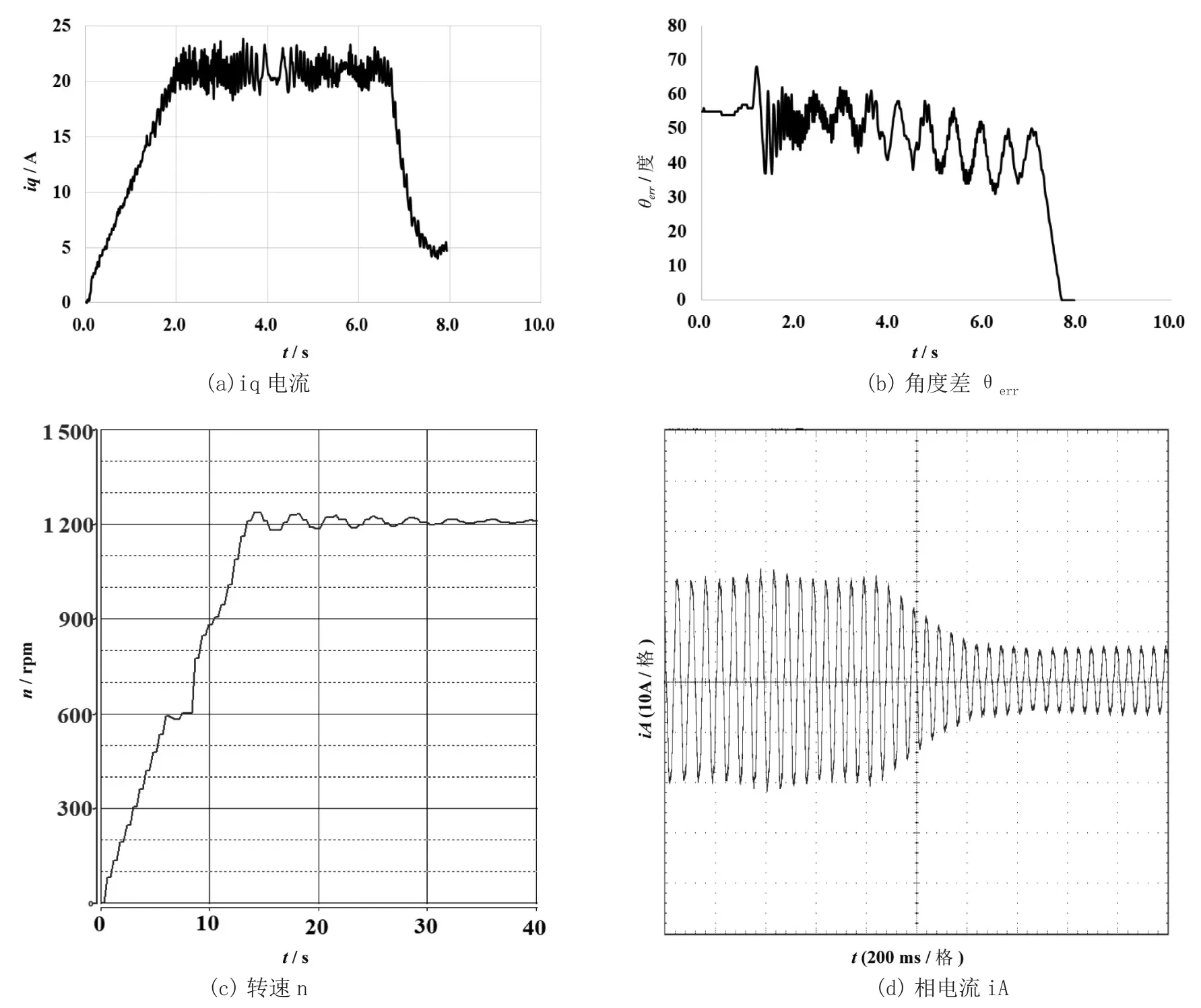
图5 K/cos2曲线控制波形
4 结 论
本文提出了一种基于改进的滑模观测器的永磁同步电机无位置传感器I-F起动方法。该改进的启动方法根据K/ cos2曲线控制电机电流完成状态切换。实验结果表明,该方法可有效减小状态切换时出现的电流扰动问题,平滑完成状态切换,提高了电机启动的成功率。

