参数自适应VMD及在高速列车轴承早期故障诊断中的应用
吴吉利, 曹洪勇, 王 旭
(中车青岛四方机车车辆股份有限公司 技术中心,山东 青岛 266111)
滚动轴承作为高速列车走行机构的重要部件,对其进行振动监测对行车安全具有重要意义。但高速列车运行时轴承振动特性较为复杂,响应信噪比低,导致共振解调计算难以在频域确定最优频带中心频率和带宽。自适应分解技术理论上能够把信号分解成具有物理意义的固有模式分量(Intrinsic Mode Functions,IMF),实现有效共振频带的选取,因此在故障诊断领域有着广泛应用。但这些自适应分解算法始终存在一些问题,导致信号分析结果不理想,或者带来更为严重的计算量。例如较为经典的经验模式分解(empirical mode decomposition,EMD)[1]及其改型[2-4],对噪声敏感,存在端点效应,且分解的分量存在严重的模式混淆,对信号变化剧烈也就是频率信息丰富的信号通常难以满足其频率分辨力要求[5]。Rilling G等[6]使用分数高斯噪声验证了其本质上是具有恒品质因数的二进滤波器组,等效滤波特性类似于小波变换,说明EMD不能实现对信号高频部分的精细划分。此外,还有局部特征尺度分解(Local characteristic-scale decomposition,LCD)[7]、局部均值分解(Local Mean Decomposition,LMD)[8]等方法也存在相关问题。为解决EMD存在的问题,Dragomiretskiy K等[9]提出了一种新式自适应分解算法——变分模式分解(Variational Mode Decomposition,VMD),它通过约束变分模型的最优解搜索,大幅降低了EMD或者它的变型中存在的端点效应及模式混淆问题。在文献[10]中,作者也通过分数阶高斯噪声验证了其等效滤波特性类似小波包,由于其滤波带宽和中心频率会随信号变换而自适应调整,因此具有比小波包更灵活的分解能力,是一种较为优秀的自适应分解算法。但VMD也存在着初始条件如模态数和平衡因子的设置问题,制约其广泛应用。
本文基于鲸鱼优化算法,提出一种参数自适应的VMD新方法,并将其应用于滚动轴承早期故障响应信号的提取,以期解决高速列车滚动轴承早期故障的识别问题。
1 基本原理
1.1 鲸鱼优化算法
鲸鱼优化算法(Whale Optimization Algorithm,WOA)是Mirjalili S等[11]基于座头鲸气泡网捕食策略提出的一种启发式的优化算法,通过设置合适的优化准则,非常适合于多参数系统的优化。WOA大致可以分三步实现。
(1)包围猎物。首先锁定猎物位置,群体包围猎物的行为可以表示为
D=|CX*(t)-X(t)|,
(1)
X(t+1)=X*(t)-A·D,
(2)
式中D表示鲸群和猎物之间的距离,X*表示当前最佳位置,X表示鲸群的位置。A和C是系数,t为当前迭代次数。可以发现,通过系数A和C的变化,鲸群的位置随之不断更新。
(2)气泡网捕食策略。气泡网策略是座头鲸独有的捕食方式,此行为可分别通过缩小环机制和依赖螺旋更新位置两种方法来描述,假设捕食过程采用这两种方法的概率为50%,那么总的策略表示为
(3)
式中D′=|X*(t)-X(t)|,b是螺旋形状的控制系数,l为[-1,1]上的随机变量。
(3)搜寻猎物。除了气泡网策略,座头鲸还会根据彼此的位置随机寻找猎物,同样基于可变向量A来实施。当|A|>1时鲸群偏离猎物,反之靠近猎物。这样能有效改善算法的全局优化特性,数学模型如下:
D=|C·Xrandom(t)-X(t)|,
(4)
X(t+1)=Xrandom(t)-A·D,
(5)
式中Xrandom为从当前种群中选择的随机位置向量。
1.2 变分模式分解(VMD)算法
VMD方法的本质是将信号分解为一系列的带限模式分量(Bandwidth Limited Intrinsic Mode Function,BLIMF),每个BLIMF被认为是一个调幅-调频信号且分布在中心频率的有限带宽内。因此,该算法的目标就是估计所有BLIMF的带宽,通常是通过以下步骤来进行的。
(1)通过希尔伯特变换计算原始信号的解析信号,调制信号的频谱到相应的基频带
(6)
(2)计算解调信号的梯度平方L2范数。约束变分模型为
(7)
(3)通过增广拉格朗日函数将式(7)的约束问题变为非约束问题,表示为

(8)
(4)采用交替方向乘子算法求解公式(8),不断更新直到求解出k个模式分量为止;
(5)使用公式(9)不断更新λn+1:
(9)
(6)对任意收敛残余项ε>0,在满足公式
(10)
的时候,终止循环。
1.3 包络谱熵
轴承故障响应信号的包络谱图应为离散的,呈周期分布的谱线,故障越明显,谱线周期性越强,熵值越小。因此可以用包络谱熵来衡量这种变化,计算公式为
(11)
式中Pi为平方包络的谱概率密度。
2 参数自适应VMD技术在轴承早期故障诊断中的流程
基于以上分析,本文提出了参数自适应的VMD轴承早期故障诊断方法,计算流程见图1。
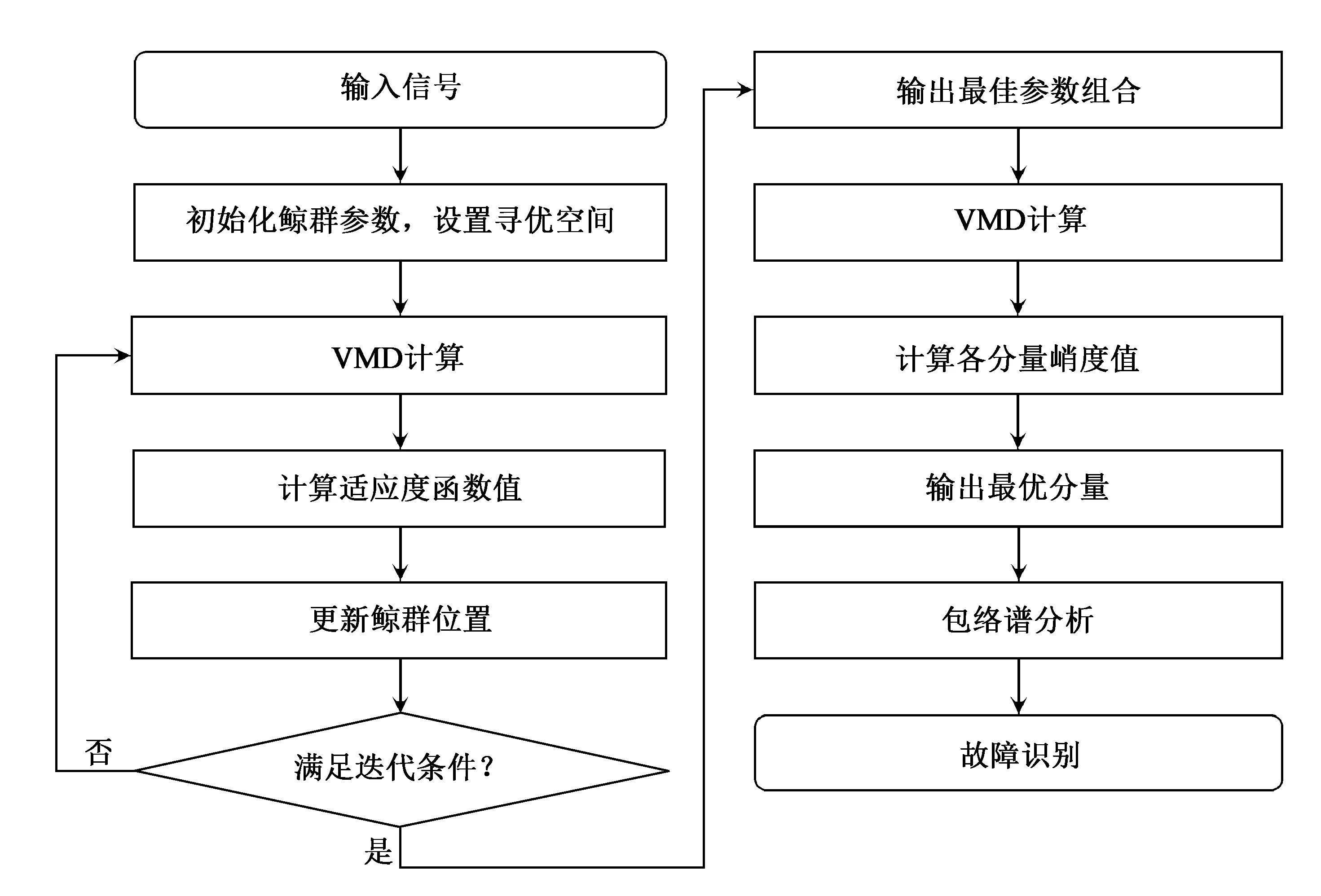
图1 参数自适应VMD轴承早期故障诊断流程
主要计算过程可归结如下:
(1)在高速列车轮组轴承座处安装加速度传感器和光电传感器,分别拾取振动响应信号和速度信号;
(2)设置鲸鱼优化算法循环初始条件:鲸群个体数为20,迭代次数为15;
(3)设置寻优空间,模态数k∈[2,12],平衡因子α∈[200,5000],其他参数为默认值,进入VMD计算;
(4)依据包络谱熵值最小准则对结果进行统计,选取熵值最小时的模态分量个数和平衡因子为最优VMD参数;
(5)将最优参数带入VMD计算,得到各个BLIMF,依据峭度准则选取敏感分量;
(6)对重构信号进行希尔伯特包络谱分析,提取故障特征。
3 仿真验证
为了验证参数自适应的VMD方法能够有效提取故障特征,给出了如公式(12)的仿真信号并通过添加高斯白噪声的方式来模拟轴承故障响应信号:
x(t)=h1(t)+h2(t)+h3(t)+W(t),
(12)
(13)
(14)
(15)
式中x(t)为轴承故障响应信号,h1(t)为轴承冲击响应信号,h2(t)为随机冲击信号,h3(t)为谐波干扰,W(t)是高斯白噪声,i和j分别为分量h1(t)和h2(t)的冲击振动次数。假设轴承的固有频率fn=2300 Hz,冲击间隔周期T=0.025 s,故障特征频率f0=1/T=40 Hz,采样频率20 kHz,采样点数为20 000,信噪比为-13 dB。那么公式(13)—(15)的仿真分量和加入噪声的时域波形可如图2所示。
根据公式(12),图2各分量构成了轴承故障响应信号。图3中同时给出了纯净信号和加噪信号的时、频域波形和包络频谱图。可以观察到,纯净信号中由于存在随机冲击和谐波分量的干扰,时域内冲击分量周期性变差,频域内出现多个谱峰,包络谱中故障特征也已经不明显。加入噪声后纯净信号的周期冲击特性被噪声淹没,包络解调后谱图上(0~300 Hz)也难以找到反映故障的特征频率及其倍频分量信息,无法对故障类型进行定性分析。该仿真信号各分量充分考虑了轴承实际工况中的各种干扰,十分适合于表述轴承早期故障振动响应信号。
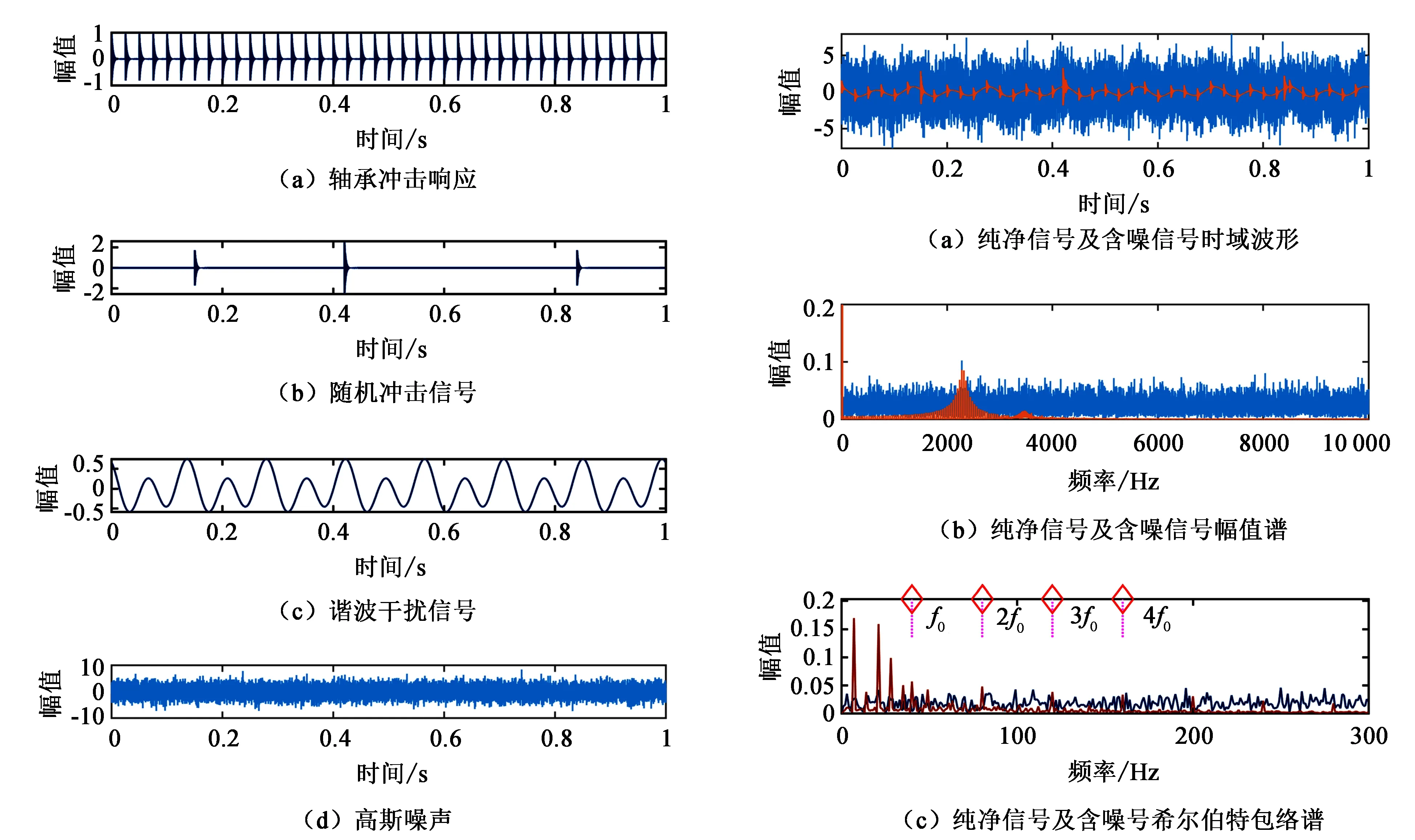
图2 仿真信号时域波形 图3 仿真信号时域波形、幅值谱及包络谱
因此我们将纯净信号采用参数自适应的VMD算法进行处理,经过15次主程序循环后适应度函数值达到最小。此时平衡因子α=3850,模态数k=9,代入VMD计算,得到c1—c9共9个带限分量。图4为各分量的频谱。

图4 各个分量在频域内的分布
图5给出了故障敏感分量c3的时域信号和希尔伯特包络谱,可见,时域波形中冲击成分明显增强,且包络谱中与故障相关的特征频率f0=40 Hz及其3个倍频分量的幅值较大,对故障指示效果明显。表明参数自适应的VMD方法能够很好地从低信噪比环境中提取到故障特征,该算法是有效的,具备工程应用价值。

图5 最优分量时域波形和包络谱
4 试验验证
试验平台为设计的某型高速列车全尺寸纯滚动试验平台,列车行走机构具有两组转向架系统,每组转向架包含两轴共2组车轮及轴箱轴承,驱动电机能驱使列车运行速度达到350 km/h。从现役列车拆卸下来的外圈轻微擦伤的轴承来模拟故障,轴承参数见表1。

表1 滚动轴承结构参数
在一组车轮靠近轴承处安装加速度传感器采集轴箱振动响应,如图6所示。振动信号采样速率为25.6 kHz,截取大约2.5 s的数据进行分析。

图6 列车轮组、轴箱及传感器安装位置
轴承故障特征频率计算公式如下:
内圈故障特征频率
外圈故障特征频率
滚动体故障特征频率
保持架故障特征频率
式中fr为转频。
根据表1参数和轴承外圈故障频率计算公式,可得到在车速约100 km/h时轴承外圈故障特征频率约为83.2 Hz。
图7为轴箱轴承座处采集到的振动响应信号,已知轴承外圈存在轻微故障时,采集到的振动响应信号、频谱和包络谱图(0~500 Hz)。可见,时域信号未出现明显的周期冲击特性,信号频谱复杂,难以确定有效共振频带,直接做包络谱也未出现故障特征频率。

图7 轴箱轴承振动响应信号 图9 最优分量时域波形和包络谱
对上面采集到的振动响应信号使用本文提出的算法进行处理,经过参数寻优迭代,当平衡因子α=4680,模态数k=7时输出最小适应度函数值。代入VMD计算,得到c1—c7共7个带限分量,各个分量在频域内的分布见图8。
类似地,图9给出了故障敏感分量c7的时域信号和希尔伯特包络谱(0~500 Hz),可见,时域中冲击分量个数明显增多,包络谱中与外圈故障相关的特征频率f0=83.2 Hz及其3个倍频分量的幅值相对明显,说明外圈存在轻微故障,与轴承实际状态相符,也表明该算法是有效的。
5 结语
由于高速列车工作环境复杂,基于振动测量方法获得轴承振动响应信号信噪比较低,难以进行有效处理,因此基于鲸鱼优化和VMD技术提出了一种参数自适应的VMD计算方法。仿真和试验的处理结果都表明,该方法能够很好地提取故障特征,是一种有效的滚动轴承早期故障识别方法。

