基于UEB模型的黄河源区黄河沿—达日区间融雪径流模拟

田明珠，赵 杰，王金钊，李铁键,2*

(1.青海大学水利电力学院，青海 西宁 810016；2.省部共建三江源生态与高原农牧业国家重点实验室，青海大学,青海 西宁 810016)

黄河源区一般指河源至唐乃亥水文站区间[1]。由于自然因素和人类活动的影响，黄河源区原始景观和脆弱的生态系统遭受了一定程度的破坏，出现了土地沙化、草原退化、水量减少乃至断流等一系列严重的生态环境问题[2-3]。这些问题不仅严重制约源区社会经济的发展，同时也影响着黄河中下游沿河地区的工农业生产和生活用水。黄河源区径流补给主要有降水、地下水和冰川融雪3种途径，分别占源区年径流量的63.15%、 9.17%和26.18%[4]。在气候变化的影响下，青藏高原降水量呈现1.43 mm/年的增加趋势，但降雪趋势的空间差异很大，东部和东北部降雪减少[5]。因此，研究降雪积累和消融的机理、分析融雪径流的季节分布规律和多年变化趋势，对更好地认识气候变化影响、合理开展水资源规划管理具有重要作用。但是，黄河源区自然条件恶劣，气象、水文监测站点稀少，对融雪产汇流过程的监测研究尤为困难。因此，采用水文模型，特别是具有物理机理的融雪径流模型，模拟和估计融雪径流成为寒区水文研究的重要手段，对气候变化影响分析、流域水资源管理及春季融雪洪水风险评估都具有重要作用[6]，也是黄河源区融雪径流研究必将采用的主要方法。

融雪径流影响因素众多，受制于寒区水文过程不确定性强，观测条件恶劣导致数据匮乏，研究基础相对薄弱，对融雪径流模拟的研究较降雨径流的研究[7]更少。主要代表性模型可分为温度指数模型(如度日因子法)、修正的温度指数模型和能量平衡模型[8]。郝振纯等[9]采用基于温度指数法的SWAT模型模拟了黄河源区地形和融雪对径流的影响，Kustas等[10]研究表明引入辐射因子后的修正温度指数模型SRM的评价系数比传统方法提高近40%。相比温度指数模型，能量平衡模型能够更好地反映积雪消融的物理过程，具有更完整的参数和更容易检测到的误差源。Tarboton等[11]基于能量和质量平衡，开发了犹他能量平衡融雪模型(Utah Energy Balance snowmelt model，UEB)，Tarboton等在美国犹他州、科罗拉多州和加利福尼亚州的多个试验点进行了UEB仿真测试和参数改进，经过校准后，模型具有较好的区域适应性。Gupta等[12]利用UEB模型对喜马拉雅地区的积雪和冰川融化进行模拟，通过输入遥感反照率和冰川轮廓，定量模拟冰川和积雪融化径流；由于缺少冰川碎屑的观测数据，模拟值的误差仍较大。Wu等[13]采用UEB模型对额尔齐斯河流域源区库威站进行了单点融雪模拟，指出UEB模型能够很好地模拟融雪过程。Liu等[14]基于3个气象站点采用UEB模型模拟 5 200 km2的玛纳斯河流域的水资源组成，认为模型精度满足研究需要。上述研究均表明，UEB模型在数据缺乏地区模拟融雪径流的良好适用性，因此，本文采用该模型对黄河源区融雪径流进行模拟。

1 数据与方法

1.1气象数据文中采用的气象数据是玛多与达日两个国家基准气象站数据，时间尺度为小时，有气温、降水、风速、湿度。为确保研究区域内气象站点资料的完整性，选取2012年10月1日至2017年9月30日的气象数据。通过SRTM DEM 90 m分辨率的原始高程数据，提取出研究区域的流域范围。气象站位置信息(表1)。

表1 气象站位置信息Tab.1 Location of weather station

为了得到研究区内的融雪分布情况，采用欧洲中期天气预报中心(ECMWF)第五代再分析数据集(ERA5)中的气象数据作为输入，但由于此气象数据中的降雨数据偏高[15]，只将此数据的输出作为分析融雪分布情况的依据，不做其他分析。

1.2研究区概况黄河源区为唐乃亥以上的黄河流域，可分为玛曲至唐乃亥区域、达日至玛曲区域、黄河沿至达日区域和黄河源头4段[16]，黄河沿到达日之间的黄河流域，总面积为24 088 km2，地理位置为97°36′～99°52′E，33°4′～35°6′N。流域覆盖达日县全境，玛多县、石渠县、玛沁县、甘德县、班玛县和称多县部分区域。研究区属高寒半湿润性气候，全年有10个月伴随积雪和降雪现象。年平均气温0.3 ℃，昼夜温差为15～ 25 ℃，年总降水量900 mm左右。地形由西北向东南倾斜，海拔3 698～5 345 m，平均海拔4 429 m。冷季风大雪多，气候寒冷且持续时间长，暖季湿润但持续时间短。研究区域如图1所示。

1.3模型简介UEB模型通过能量和质量平衡计算来跟踪地表单个雪层的积累和消融。该模型考虑了冠层雪的拦截、入射太阳辐射和大气辐射通过冠层的分配，以及冠层内外潜热和感热的湍流通量。研究区中植被多为草地，且高度不高，故不考虑冠层的影响。模型的输入变量包括气象数据和太阳辐射，本研究太阳辐射量通过气温在模型中进行计算。模型可采用0.5、1、6 h的时间步长，本文选择1 h步长进行模拟。

UEB模型采用3个状态变量：雪水当量W(m)、能量含量U(kJ /m2)和雪面年龄来描述雪的堆积过程。能量含量用于确定积雪的平均温度和液态水含量，雪面无量纲年龄仅用于计算积雪表面反照率。状态变量U和W在时间上的变化由以下能量和质量平衡来确定，能量平衡方程见式(1)。

(1)

式中：所有项的单位均为kJ /(m2·h)，Qsn为太阳净辐射；Qli表示入射长波辐射；Qp为降水平流热；Qg为地热通量；Qh和Qe分别表示感热通量和潜热通量；Qle为传出长波辐射；Qm表示融水平流的热量。质量平衡方程见式(2)。

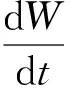
(2)

式中：所有项的单位均为m/h，Pr为降雨速率；Ps为降雪速率；Mr为从积雪中流出的融水；E为积雪的升华。

模型需输入气象数据，所选择的研究区内包含两个国家基准气象站，用泰森多边形法[17]把研究区分为两个流域，一个子流域用玛多气象站的数据运行，另一个子流域用达日气象站的数据运行，最后统计这两个流域的运行结果进行分析。分割结果如图2所示。

1.4模拟效果评价标准本研究采用纳什效率系数(NSE)和相对误差(Re)定量评估基于实测径流量的模型准确性。计算公式如下：

(3)

(4)

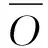
来自雪融水、雨水的地表水输入等产出在流域上聚集。由于雪和雨水是产生河流的输入，这些被称为地表水输入分量，这些分量的总和称为地表水输入总量。

总地表水输入(SWIT)=融雪地表水输入(SWISM)+雨水地表水输入(SWIR)

(5)

利用模拟的SWIT计算的月SWIT值与月径流深度(R)进行比较。这里月径流深度是用月总水量(Wq,m3)除以流域面积(F,km2)计算出来的，是一种面积标准化的流量度量，相当于计算期间的平均水深。计算公式如下：

R=Wq/1 000F

(6)

1.5参数率定根据模型说明总结参数，确定各个参数的变化范围并调参。经手动调参，发现参数变化对输出变量的值并无影响。最后确定各参数的值如下：降雨临界温度Tr和降雪临界温度Ts是模型计算的关键参数，确定Tr为1～3 ℃，取为3 ℃，Ts为-1～0 ℃，取-0.3 ℃。其他可调试的参数：雪的密度(150～450 kg /m3)，取为337 kg /m3；雪的辐射系数，可为0.98、0.99，取0.98；表面空气动力学粗糙度(0.005～0.02 m)，取0.005 m；饱和水导率(20～25 m/h)，取20 m/h；地面热容为2.09 kJ/(kg·℃)，雪的液体容纳能力为0.05，新雪可见光波段反照率0.90，新雪近红外波段反射率为0.6，裸露地面反照率为0.25。

2 结果与分析

模型采用2012年10月1日至2017年9月30日小时尺度的气象数据。雪水当量初始条件、积雪内能和表层土壤内能、雪面年龄设定为零，导致了在模拟开始时的误差，随着模型适应驱动输入的时间逐渐减小。在这些初始误差减小之后再分析结果最有意义。

2.1模拟降雪与实测现象输入模型的降水为小时数据，所以也可是降水速率。模型运行时会把降水分为液态降水和固态降水，统计24 h的数据将液态降水记为PR，固态降水记为PS。玛多县的降雪集中在4—5月和9—10月。模拟结果与玛多气象站实际监测结果一致，图3a为玛多县2013年5月气象站观测的天气现象对应的降水与降雪。根据临界气温统计出降雪量与降雨量，降雪量占总降水量的20%左右。年际间降雪量呈现波动趋势，2015年的降雪量达到最大值，为99.3 mm。2014年和2016年的降雪量相当，2017年降雪在五年之中最少，仅有51.2 mm。

达日县的降水量及时间分布趋势，与玛多县有较大差异，达日县在每年的10月至翌年4月以降雪为主，雨夹雪多发生在5月至6月初和9月，6—8月以降雨为主。图3b为达日县2014年4月气象站观测的天气现象对应的降水与降雪，总体上看，模拟效果较好。根据临界气温统计出降雪量与降雨量，降雪量占总降水量的15%左右。达日县降雪量年际间相差不大，在2014年10月至2015年9月的降雪量较其他年少，仅有71 mm，其他年份的降雪量在90～110 mm。

2.2积雪消融与气温的关系模型模拟了融雪地表水输入和雨水地表水输入。图4为两区域SWISM和气温(Ta)随时间的变化，可以看出融雪主要在每年的4月至6月初和9—10月。而达日县的融雪则会多于玛多县，两者相差20 mm。4—6月为春季融雪，天气回暖，冬季积累的雪开始融化，对径流产生不可忽视的影响。9月研究区域开始下雪，但气温条件并不能形成积雪，多数转化为径流流出。故在这两个时段的融雪对地表水总输入贡献较大。

图5为选取的两区域典型时段内SWISM与PS随时间的变化，图5a为玛多县，选取的是春季时期，图5b为达日县选取的是秋季时期。由图5可以看出它们之间有很明显的相关关系，随着PS增加，SWISM也会增加，但在时间上会晚于PS。

2.3模型模拟的径流研究区域2012年10月至2017年9月实测径流深与模拟径流深整体上拟合程度较好。从模型结构和输出结果看，模型模拟结果SWIT为径流产生数据，实测径流为汇流结果数据。从径流产生到汇流的过程涉及水的损失，如地下渗透、水的蒸发和植被的截留，模型没有考虑到这些损失，故模拟径流在汛期与实测径流相比偏高。由图6可知，在汛期SWIT的值大于月径流深度(R)，且SWIT的总体上升趋势早于R。这一结果表示该流域具有相当大的储存潜力，可能以地下水储存的形式，因此需要一段时间才能饱和并开始产生径流。模拟径流在每年11月至翌年3月径流是非常小甚至没有，因为模型没有考虑到在积雪下面土层中的热量产生的积流，所以会有一些误差。

通过计算本研究的NSE为0.85，Re为-0.10，但如果不加上融雪输入量与实测径流相对比，得出的NSE为0.79，相对误差Re为-0.14，说明融雪对该区域的模拟径流有改进且不可忽视的作用。总体来说，该研究构建的模型能够较好地模拟研究区的径流情况。

2.4融雪量的分布根据输入的ERA5栅格数据表示研究区内的SWISM分布，ERA5气象数据分辨率为0.25°，故流域分辨率为0.25°。选取融雪径流量较为典型的月份进行分析。图7为2015年2月研究区内的SWISM分布。由图7可知，SWISM主要分布在研究区的北部和中南部，根据地形分析确定SWISM高的区域海拔较高，原因是高海拔地区气温较低，有大量积雪，故积雪融化量也会较高。

2.5不同水源的贡献率总地表水输入源分为降雨流入和融雪输入。一般来说，降水在总地表水输入中占比最大，在进行模拟的这五年中，融雪对地表水总输入的贡献率相差不大，都在4%左右。如图8a所示，2016年融雪贡献率为最大。但用ERA5数据模拟的融雪径流平均为46%。如图8b所示，也是2016年融雪贡献率为最大。但由于ERA5数据中的降水量偏高，模拟出的径流量与实测相比也偏高，还需进一步研究。

3 讨论与结论

黄河源区水文特征复杂多变，目前仍是研究的热点区域之一。本研究利用UEB能量平衡模型，对黄河源区黄河沿—达日段2012年10月至2017年9月的气象数据进行模拟。在达日县与玛多县，模拟的降雨和降雪情况，其结果与地面气象站监测结果相似，即两者在天气现象和降水状态上具有较好的一致性。通过分析积雪消融与气温的关系，融雪发生的主要时间为每年4月至6月初和9—10月。在径流深的模拟中，与实测径流深拟合度较高。从融雪量的分布上来看，SWISM与海拔高度呈正相关。与Wu等[13]和Liu等[14]研究相比，整体来看，UEB模型在黄河源区有很好的适应性，能为观测资料稀缺地区冰雪融水研究提供支撑。本研究结果还存在一定局限性，对11月至翌年3月的径流模拟结果偏差较大，对地形上的融雪径流模拟还需进一步研究。在以后的研究中，可以对模型进行改进，加入冰川融化对径流的影响，进一步分析黄河源区的水源。