青海MODIS可降水量数据校正研究

王 佳，李 琼，魏加华,3*

(1.青海大学水利电力学院，青海 西宁 810016；2.三江源生态与高原农牧业国家重点实验室，青海大学， 青海 西宁 810016；3.清华大学水沙科学与水利水电工程国家重点实验室，北京 100084)

大气可降水量(Precipitable Water Vapor，PWV)表示地面至大气顶界垂直空气柱中全部水汽凝结后在气柱底面上形成的液态水深度[1]。PWV作为水汽含量的衡量标准，对监测及预报全球或局地气候变化及中小尺度恶劣天气至关重要[2-5]。无线电探空仪、GNSS(Global Navigation Satellite System，GNSS)和遥感探测是大气可降水量观测的主要手段。无线电探空仪精度高，但时间分辨率较低，多用于精度的验证；GNSS具有高精度、低费用、时间分辨率高的优势[6-9]，但空间分辨率受地面观测站点密度的影响较大。遥感卫星探测数据覆盖广，空间分辨率较高。MODIS水汽产品空间分辨率可达到1 km[10-11]，但其受天气条件与搭载的传感器性能等影响精度有限[12]，需要进一步的精度校正。

结合地基探测数据对遥感水汽产品进行校正，以获得更高时空分辨率、更高精度的数据是目前大气可降水量数据获取的一种有效方式。曹艳丰等[13]、方圣辉等[14]研究了不同区域GNSS PWV数据与MODIS PWV数据间的线性关系，并建立了回归模型，对MODIS PWV数据进行校正并获得了高精度的可降水量数据。但由于影响可降水量的因素较多，简单的线性回归模型在地形复杂区域适用性会降低。神经网络模型具有很强的容错性以及自学习、自组织与自适应能力，可以模拟复杂的非线性映射，使得环境噪声(气溶胶、云等)的影响降到最低。

获得高精度且连续的可降水量数据，对研究区域气候的变化，评估降水潜力具有非常重要的作用。本文采用线性回归与BP(Back Propagation，BP)神经网络方法，建立利用GNSS PWV数据校正MODIS PWV数据的模型，并利用探空数据检验模型的校正效果。

1 数据资料以及分析方法

1.1 研究范围、站点及资料

青海省位于中国西北地区中南部，青藏高原东北部，处于气候变化的敏感区。气候类型复杂多样，具有明显的高原气候特征，寒冷干燥，太阳辐射强，气温日较差较大[15]。青海省复杂的下垫面对地气间能量和水分交换过程有重要影响，从而影响水汽的时空分布变化。

研究采用的数据包括无线电探空数据、地基GNSS反演的PWV数据和MODIS PWV数据(2016年)。无线电探空站在青海省内有玉树、西宁、格尔木和都兰4个站点，每日观测两次，数据来源于怀俄明大学(http://weather.uwyo.edu/wyoming/)，用SOUNDING表示。地基GNSS站在青海省内有15个连续运行的站点，时间分辨率为1 h，数据来源于中国地震局GNSS数据产品服务平台(http://www.cgps.ac.cn)。无线电探空站和GNSS站点具体信息如表1所示。

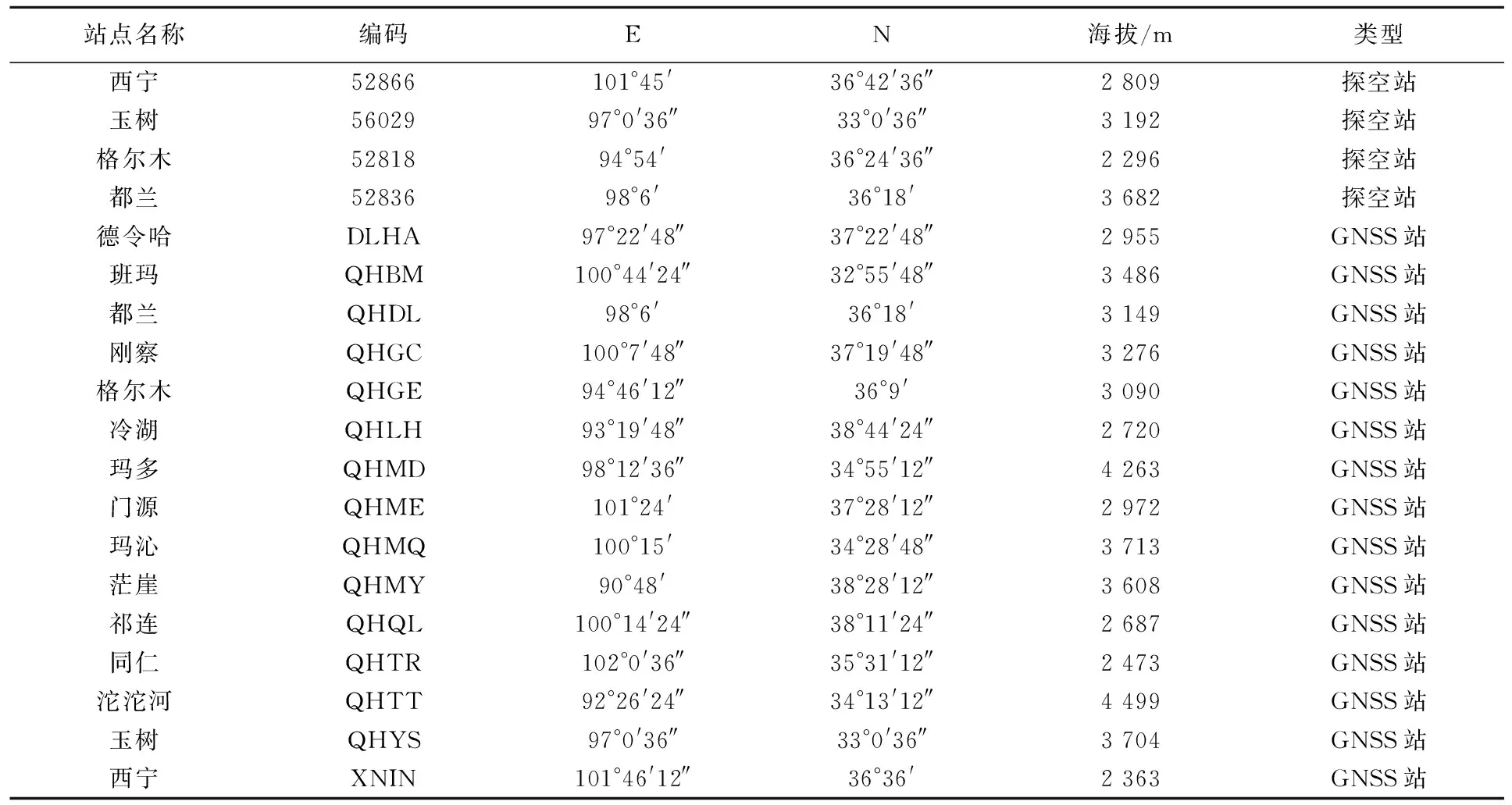
表1 地面站点信息Tab.1 Information of ground station

MODIS数据来自EOS系列卫星中TERRA卫星上搭载的中分辨率光谱成像仪反演得到的MOD05产品，数据下载地址为https://modis.gsfc.nasa.gov/。研究使用的近红外水汽产品空间分辨率为1 km×1 km，每天只有1幅观测图像，本研究选取GNSS与MODIS时间相匹配的数据。

1.2 分析方法

1.2.1 线性回归分析法 线性回归是利用数理统计中回归分析的方法，来确定两种或两种以上变量间相互依赖的定量关系，被广泛应用于气象水文领域[16]。对MODIS PWV进行校正时，以月为尺度进行模型构建，式(1)为本研究采用的线性回归模型表达式：

PWVGNSS=PWVMODIS×a+b

(1)

式中：PWVGNSS、PWVMODIS分别为GNSS PWV的值与MODIS PWV的值，a为模型系数，b为常数。

1.2.2 BP神经网络 BP神经网络又被称为误差反向传播神经网络，是一种多层的前向神经网络[17-18]，具有自适应学习性，可以模拟输入—输出间的非线性关系，减少缺测值对模型的影响。本文以GNSS站点经纬度为中心，筛选3×3窗口范围内的MODIS PWV与相应的GNSS PWV进行匹配，建立数据集，并将其以7∶3的比例随机抽取分为训练集与测试集。如图3所示，以对应的MODIS PWVn及其经纬度(lonn，latn)为输入，经输入层i，根据权值W(i,j)和隐藏层阈值a，计算得到隐藏层j的输出Zq。再经由权值V(j,k)和输出层阈值b计算得到神经网络预期输出，与期望输出GNSS PWV及其经纬度(lon′，lat′)比较并计算网络预测误差，根据计算得来的误差更新权值和阈值，直到误差减小到预期范围，结束迭代，网络训练结束。另外，为了减少数据之间量级的差异对网络精度的影响，在训练前先将数据进行归一化。

2 MODIS大气可降水量校正

Wang等[19]利用GNSS PWV对MODIS PWV数据的精度做过验证，表明GNSS PWV与MODIS PWV间存在良好的相关性且GNSS PWV精度更高，但GNSS PWV的空间分辨率不足；而MODIS PWV空间连续且覆盖范围大，但精度略差。本文利用玉树(QHYS)、格尔木(QHGE)、西宁(XNIN)和都兰(QHDL)4个无线电探空站点数据计算GNSS PWV与MODIS PWV数据的均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MRE)和相关系数(r)对青海省内的GNSS PWV与MODIS PWV做简单的精度评估。

2.1 GNSS PWV与MODIS PWV的精度验证

根据表2中计算得到各个站点的误差可以发现，GNSS PWV数据平均偏差为1～2 mm，相关系数除都兰站外均为0.9～1，显示GNSS PWV数据与探空数据之间较强的相关性。而MODIS PWV数据相较GNSS PWV数据整体偏差较大，平均偏差为1～6 mm，存在校正的必要性。

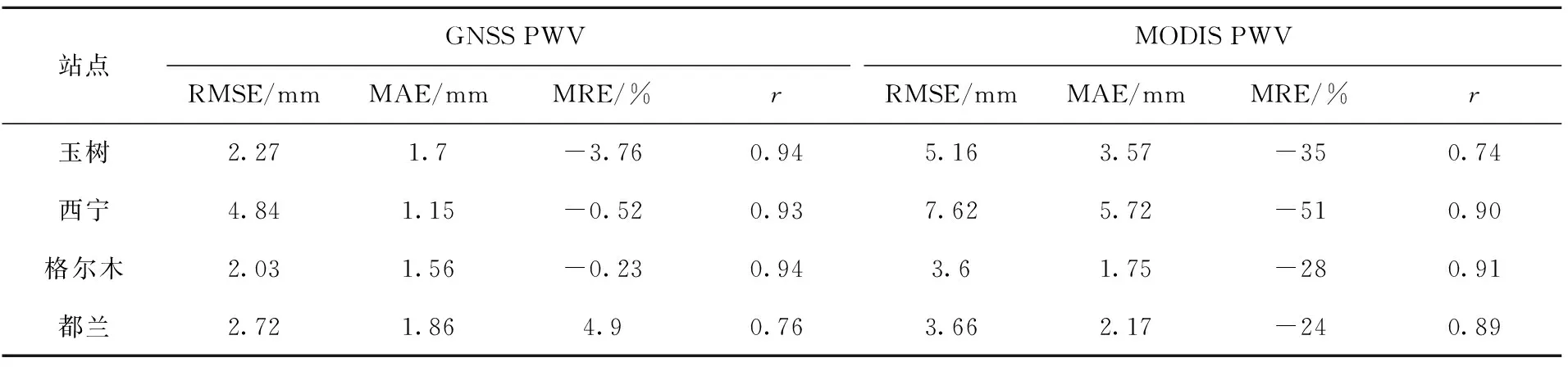
表2 GNSS PWV与MODIS PWV原始数据精度评估表Tab.2 Accuracy evaluation of original data of GNSS PWV and MODIS PWV

如图2所示，4个站点的GNSS PWV与探空数据相关性高，存在良好的线性关系，玉树，格尔木，西宁3个站点GNSS PWV数据与探空数据在30 mm以下均保持着很强的相关性，但都兰站GNSS PWV数据与探空数据仅在10 mm以下的相关性比较强，这与都兰站的观测受到气候影响有关。而相对于GNSS PWV而言，图3中MODIS PWV数据与探空数据的相关性整体偏弱，说明MODIS PWV数据较GNSS PWV数据偏差大，精度低。

2.2 GNSS PWV数据与MODIS PWV数据的相关性

为了检验GNSS PWV与MODIS PWV的相关性，从15个GNSS站点中随机选取几个站点研究各站点之间PWV的趋势变化及相关性(图4)。

在图4a中，选取站点为德令哈、格尔木和西宁，可以看出，这些站点的MODIS PWV与GNSS PWV变化趋势基本相同，都呈现中间(夏季)高，两边(冬季)低的特征。由图4b至图4d可知，德令哈、西宁和沱沱河单个站点的GNSS PWV与各自对应区域的MODIS PWV均有良好的相关性。由此得出，MODIS PWV数据与GNSS PWV数据之间整体都有比较好的相关性，为利用GNSS PWV数据校正MODIS PWV数据提供了基础。

2.3 基于线性回归的校正

GNSS数据存在缺失情况，剔除缺测值后，将15个地基GNSS站2016年的数据与MODIS PWV数据按月匹配，根据式(1)中的方法，计算系数，得到基于最小二乘法的各月的回归模型(表3)。

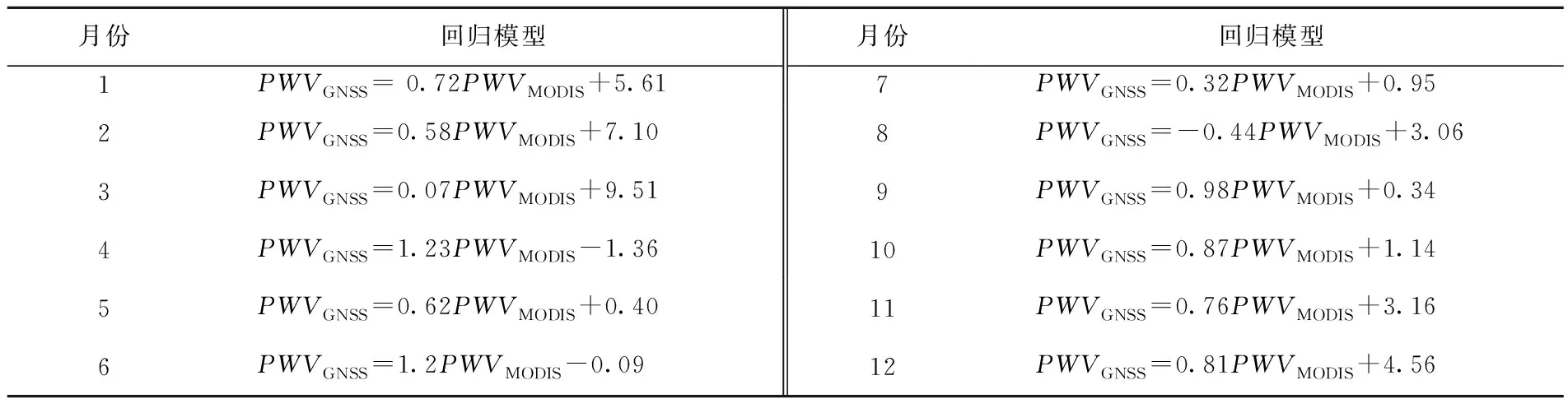
表3 逐月回归模型Tab.3 Monthly regression model

2.4 基于BP神经网络的校正

本文在进行BP神经网络建模时，根据MODIS PWV与GNSS PWV数据的特性，利用站点的GNSS PWV校正部分区域内的MODIS PWV。神经网络模型的构建主要有以下几个步骤：

(1)数据的导入与划分。根据融合数据的特性，以GNSS PWV数据的经纬度为中心的，将需要校正的数据(MODIS PWV)与目标数据(GNSS PWV)根据经纬度匹配，建立数据集，并按照训练数据70%，测试数据30%的比例进行划分。

(2)确定隐藏层个数。输入层神经元设定为9,输出层神经元为1。隐藏层神经元个数根据经验公式确定取值范围为[3,13]，经过测试并考虑到模型的复杂度且避免过拟合的需求，最终确定隐藏层神经元个数为10。

(3)网络初始化。给各连接权值分别赋值(-1,1)之间的随机数，设定激活函数为sigmod函数，损失函数应用RMSE函数。最后经过调整学习率μ为1.5，控制误差ε在0.05范围内。

2.5 模型精度验证

利用玉树、西宁、格尔木、都兰4个探空站数据对两组模型校正后的MODIS PWV数据进行评价，分析其校正效果。由图5可以看出利用两种模型得到的校正后数据的均方根误差与平均绝对误差皆逐渐减小。

由表4可以看出，线性回归结果中玉树、西宁、格尔木3个站点较都兰效果更好，均方根误差平均降低了1.24 mm，平均绝对误差平均降低了1.1 mm，平均相对误差平均降低了13%。整体校正效果较好，但在都兰地区校正效果不太明显，均方根误差降低了0.6 mm，平均绝对误差降低了0.47 mm，平均相对误差降低了仅4%。考虑到青海地区地理面积大，但站点稀疏、站点间海拔相差较大，对线性回归模型存在影响。所以在不同站点上对MODIS PWV数据的校正结果存在一定差异性。从计算结果来看，线性回归校正模型在青海地区对数据的精度提升有一定的效果，但是，BP神经网络模型校正后的MODIS PWV数据精度评价效果更好，与未校正前的数据相比，均方根误差平均降低了2.46 mm，平均绝对误差平均降低了0.947 mm，平均相对误差平均降低了19.25%。总之，具有自适应性的BP神经网络模型对MODIS PWV数据的校正效果更好。

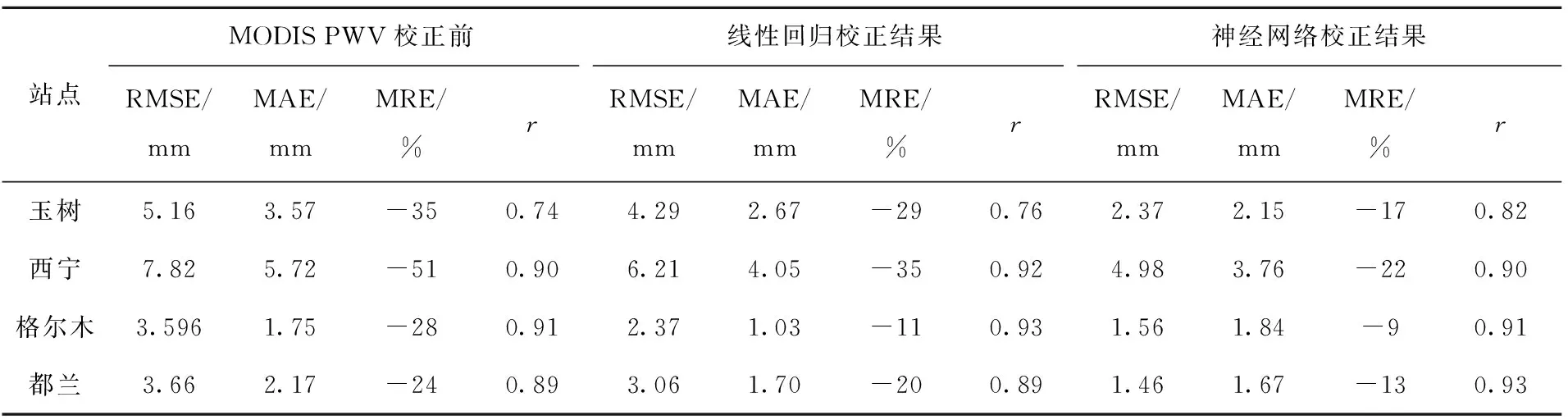
表4 MODIS数据校正前后精度评价表Tab.4 Accuracy evaluation of MODIS data before and after correction

3 讨论与结论

大气可降水量反映了区域水汽条件和降水潜力。青海省地域广阔，地形复杂，大气可降水量差异显著，获得高精度且空间连续的大气可降水量对区域生态、农业生产、水资源管理等具有重要意义。方圣辉等[14]仅根据4个地面站点对全国范围的大气可降水量建立了线性回归分析模型，仅仅提高了精度并不能反映连续的空间变化。而曹艳丰等[13]、王茜雯等[20]利用地面站点数据分别对美国及香港地区GNSS站点密集区域的MODIS PWV建立了线性回归校正模型，表明线性回归校正模型在地面站点密集的区域有良好的校正效果，但针对青海省这种地貌复杂，站点稀疏的区域，线性回归模型的效果尚未确定。因此本文通过对青海省GNSS的资料进行处理分析，利用不同观测手段之间可降水量数据的相关性，分别应用线性回归方法与BP神经网络方法结合GNSS PWV数据对MODIS PWV数据进行校正研究，依据校正后的数据，分析两种模型在站点稀疏区域的校正效果，得到以下结论：

(1)利用GNSS PWV数据校正MODIS PWV数据是行之有效的，线性回归模型和BP神经网络模型得到的结果精度均在毫米级以内，可以应用到后续的研究中；

(2)BP神经网络模型效果好于线性回归模型，应用四个无线探空站点数据对结果进行检验，平均相对误差整体上由3.24 mm减少到2.35 mm，精度提升了27%，说明神经网络方法能更好地拟合GNSS PWV数据与MODIS PWV数据之间的关系，对MODIS PWV的校正效果更好。

本文仅对MODIS PWV的精度提升进行了研究，获得了高精度空间连续的可降水量数据集，但水汽变化快速复杂。因此，在下一步的研究中将着重提高MODIS PWV的时间连续性，在时间尺度上分析其变化规律，为临近预报和人工降雨等提供有力支撑。