考虑搅拌筒动态质心的搅拌车抗侧翻控制研究

干年妃，雷富强，周兵†，吴晓建，李涛，柴天

（1.湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082；2.南昌大学机电工程学院，江西南昌 330031）

近年来，重型商用车由于侧翻事故造成的伤亡人数逐渐递增.搅拌车作为一种特殊的重型商用车，一方面，质量大、质心高、车身较长，导致控制困难；另一方面，搅拌筒在行车过程中动态运转，带动混凝土使其重心向转动方向偏移，对底盘造成偏心载荷.特别地，在转弯过程中，混凝土因其流动性及离心力的影响，造成载荷外移，且伴有动态冲击，速度稍高时，车辆的侧倾稳定性变差，易引发侧翻事故.因此，研究搅拌筒动态质心变化并分析其对搅拌车侧翻稳定性的影响，进行搅拌车抗侧翻控制，提高搅拌车侧翻稳定性具有重要意义.

学者们对混凝土的搅拌过程、搅拌机理以及商用车侧倾稳定性与防侧翻控制做了大量的研究.Tan[1]、Cao[2]、Xiao[3-4]、Deng[5-8]等人所在的课题组根据离散单元法（DEM）对混凝土运动进行了深入的研究，分析了混凝土与混凝土之间、混凝土与搅拌筒壁之间的相互作用，进一步研究了搅拌筒的搅拌机理.并且，对混凝土搅拌的影响因素、离析的问题都做了深入的探索.Sankar[9]等人对车辆进行灵敏度分析，得到影响侧翻的部分参数，通过优化参数提高车辆的侧倾稳定性.随着计算机技术、非线性动力学的发展，在车辆的稳定研究过程中引入各种非线性稳定理论[10-13].Yoon 等[14]考虑各种动力学约束，通过绘制侧倾角-侧倾角速度相平面来分析车辆的稳定性区域分布.金智林[15]等人将设计的驾驶员模型融合到多自由度的汽车侧翻动力学模型构成人-车闭环系统，分析了驾驶员对汽车侧翻稳定性的影响，进行了防侧翻控制研究.Goldman[16]等人采用侧向加速度、侧倾角与预设的阈值作比较来判断侧翻.Riofrio 等[17]采用动态门限值横向载荷转移率为侧翻评价指标.Hyun 等[18]在考虑车辆的非线性、模型参数辨识的基础上，利用横向载荷转移率作为侧翻指标.Chen 等[19]提出运用侧翻预警时间作为侧翻指标（TTR），提高TTR 精度的同时，实现了动态预警.Li[20-26]等人结合滑模控制、模型预测控制（MPC）等设计主动前轮转向（AFS），横摆力矩控制（DYC）防侧翻策略.

以往研究者们的重点主要是搅拌车自身结构优化、搅拌筒的搅拌机理及混凝土运动过程的探索.缺乏对搅拌筒的动态质心运动分析且将其考虑到搅拌车的侧翻控制中去的研究，忽略混凝土自身的流动性和搅拌筒转动引起的动态质心偏移对搅拌车的侧倾稳定性影响.

为提高搅拌车的侧翻稳定性，本文考虑搅拌筒动态质心，结合离散元法建立数学模型并创新应用方法，提出一种基于差动制动，改进粒子群算法融合PID 控制决策对车轮施加制动力的抗侧翻控制策略.利用EDEM 软件对混凝土的搅拌运动进行模拟，输出混凝土的质心位置数据，拟合得到混凝土的动态质心数学模型.而后，建立搅拌筒动态质心的位置变化与搅拌筒支承力的关系，施加到Adams car 多体动力学整车模型仿真中，分析其对搅拌车稳定性的影响.最终，采用电子机械制动系统（EMB）对车轮施加制动力，以差动制动为理论依据，横向载荷转移率（LTR）为侧翻指标，设计了一种与智能优化算法结合的自整定PID 抗侧翻控制系统.防侧翻控制仿真分析结果证明了本文方法的有效性.

1 搅拌筒动态质心建模及分析

1.1 搅拌筒动态质心建模

搅拌车行驶过程中，混凝土在搅拌筒内的运动状态很复杂.以往的研究大多数是通过对混凝土的复杂流动状态进行简化，建立比较简单的数学模型来表征搅拌筒质心的动态变化.一方面，由于纯粹的数学推导限制，建立的数学模型忽略了很多实际因素；另一方面，这些模型根据理论建立之后没有进一步地应用到整车分析中去.由于数据条件所限，本文选择搅拌车满载时的情况，根据国标对普通混凝土的试验要求[27]，基于离散单元法（Discrete Element Method）理论，通过EDEM 软件对混凝土的搅拌运动进行模拟，输出混凝土的质心位置数据.在此基础之上，利用计算机辅助，拟合数据得到搅拌筒质心各个方向的位移随时间变化的数学模型.该模型与之前的纯数学理论推导相比，在一定程度上能更好地反映搅拌车在实际运输过程中搅拌筒质心的动态变化，为搅拌车的研究设计提供更加真实可靠的依据.

搅拌筒轴向为x 轴，垂直于轴线方向的平面为yoz 平面构建坐标系，建立搅拌筒离散元模型如图1所示.如前所述，搅拌混凝土的流动状态很复杂，由于各种条件限制，研究过程中也做了一定的简化，在建模和后续的分析时，忽略了搅拌筒轴向的位移.利用离散元法认为混凝土由粗骨料和砂浆颗粒组成，参照搅拌筒的实际转速，仿真分析时分别设置搅拌筒的转速为3 r/min、8 r/min.

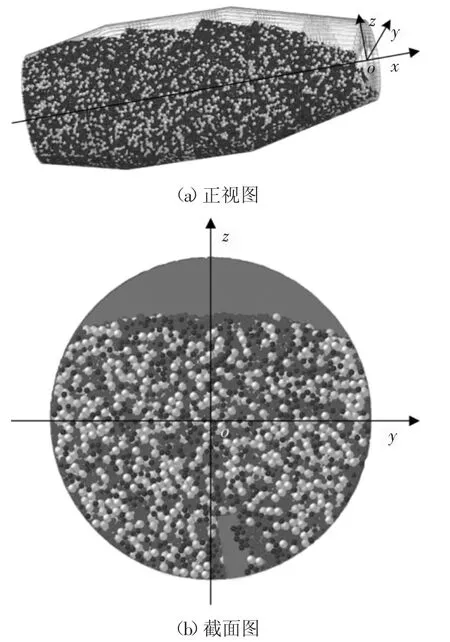
图1 仿真基本信息和颗粒的状态Fig.1 Basic information of simulation and the state of particles

根据输出的离散数据，计算混凝土的质心，一个连续分布的质心是无数个质点的集合，将混凝土颗粒看作质点，所有颗粒的质心位置的集合就是混凝土的质心，质心坐标计算如下：

式中：y0为混凝土动态质心到z 轴的距离，z0为混凝土动态质心到y 轴的距离，i=1，2，3，…，n，n 为微粒的总数，mi、yi、zi分别表示微粒i 的质量、微粒动态质心到y 轴的距离、微粒动态质心到z 轴的距离，m 为混凝土的总质量.

通过以上的仿真和计算，可得到搅拌筒y、z 方向质心位置随时间变化的离散的点，利用MATLAB拟合工具箱得到质心位置随时间连续变化的数学模型，如式（2）-式（5）所示，y3、z3为搅拌筒转速为3 r/min 时y、z 方向质心位置随时间变化的函数，y8、z8为搅拌筒转速为8 r/min 时y、z 方向质心位置随时间变化的函数.随着搅拌筒转速不同，质心位置变化的大小随之改变.

研究结果表明，在搅拌筒的转速不超过8 r/min时，y 方向质心位置变化最大为0.25 m，z 方向质心位置变化最大为0.41 m.

1.2 动态质心模型的应用

进一步研究发现，目前的技术无法实现Adams car 多体动力学整车模型与离散元模型的直接联合仿真.考虑到搅拌筒及混凝土对搅拌车的影响是一种力的互相作用，建立搅拌筒动态质心的位置变化与搅拌筒支承力的关系，需要对搅拌筒的受力研究分析.

搅拌车的搅拌筒受力分析如图2 所示，搅拌筒的质量主要由三个位置支承.搅拌筒的前端是通过一个法兰与减速机相连，减速机带动搅拌筒旋转，而搅拌筒的后端上设计有环形滚道，与滚道接触的是车身后支架上的两个对称分布的滚轮，这样的设计可以减少其运动过程中受到的阻力，并且，两个滚轮的支承合力方向始终经过一点，有利于提高搅拌筒在搅拌车行驶过程中的稳定性.搅拌筒安装倾斜角度ε=15°，两滚轮与搅拌筒的夹角是φ，搅拌筒的转速为ω0.

图2 混凝土搅拌筒受力分析Fig.2 Force analysis of the concrete mixing drum

在对搅拌车的搅拌筒力学分析前，做以下假设：所有的轴承内圈安装与其他的物体配合紧密，并且，不会发生相对滑动；忽略轴承座的加工安装误差；无轴承游隙误差，滚道接触处于弹性变形范围；转动的搅拌筒假想为空心轴，运动过程中有弹性变形时，其截面形状和截面几何尺寸永远不发生变化.

如图2 所示，根据物体的受力平衡，有如下力平衡方程：

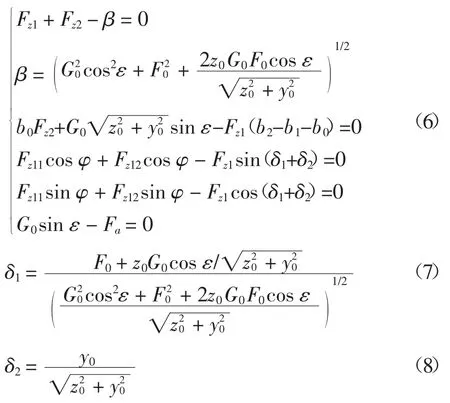
式中：偏距y0、z0分别在我们前面工作中对搅拌筒质心的动态坐标公式的研究中已经求出，G0、F0分别为搅拌筒工作时的重力和离心力，Fz2、Fa分别为左端轴承的径向力和轴向力，Fz1为滚轮的支承力（左右滚轮支承力Fz11和Fz12的合力），b0为左端支承到重心的距离，b2为左端支承到搅拌筒最右端的距离，b1为右端支承到搅拌筒最右端的距离.

2 混凝土搅拌运输车转弯时稳定性分析

基于建立的Adams car 多体动力学整车模型，如图3 所示，将1.2 节计算出来的作用力施加到左端支承位置和右端两滚轮支承位置，理论上搅拌筒以不同的转速运动时，对车辆的稳定性产生不同程度的影响.转向盘角阶跃输入工况和Fishhook 工况下，根据混凝土搅拌运输车现实的运输情景，分别在0 r/min、3 r/min、8 r/min 的搅拌筒转速下进行仿真分析，两种试验工况行驶速度均为45 km/h，方向盘转角输入如图4 所示，后文两种工况下的方向盘转角不变.

图3 Adams car 整车模型Fig.3 Assemble vehicle model

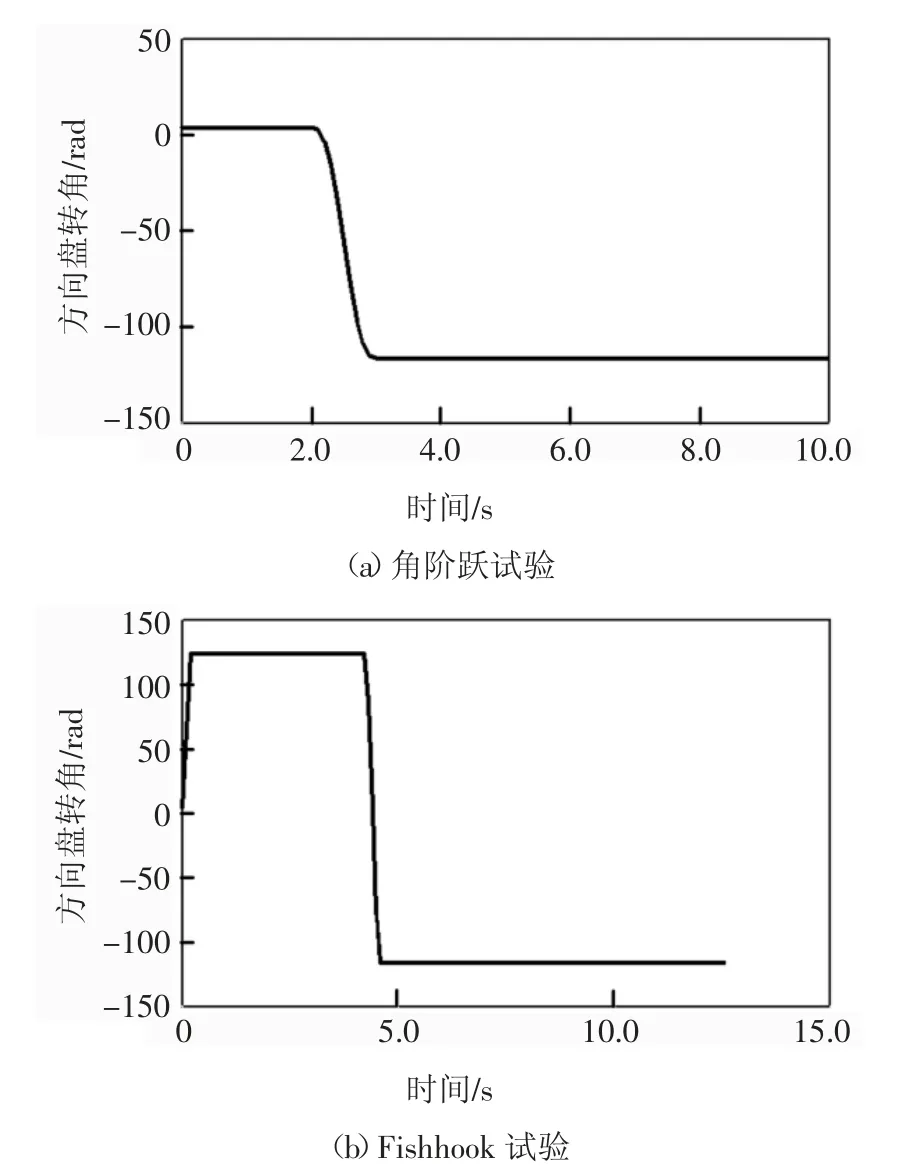
图4 方向盘转角Fig.4 Steering wheel angle

仿真分析结果如图5-图7 所示，由图可知，随着混凝土搅拌筒转速的升高，搅拌车的侧向加速度、侧倾角、侧向位移明显增大.搅拌筒转速为8 r/min时，侧向加速度与3 r/min 时的最大差距达到约500 mm/s2，且侧向加速度、侧倾角的波动比较剧烈，侧向位移明显增大.仿真结果表明，搅拌筒转速较高时，搅拌车转弯的时候侧翻稳定性降低，如果此时的行驶速度再增加，车辆很容易发生侧翻.因此，搅拌车在转弯的时候一定要注意减速慢行.

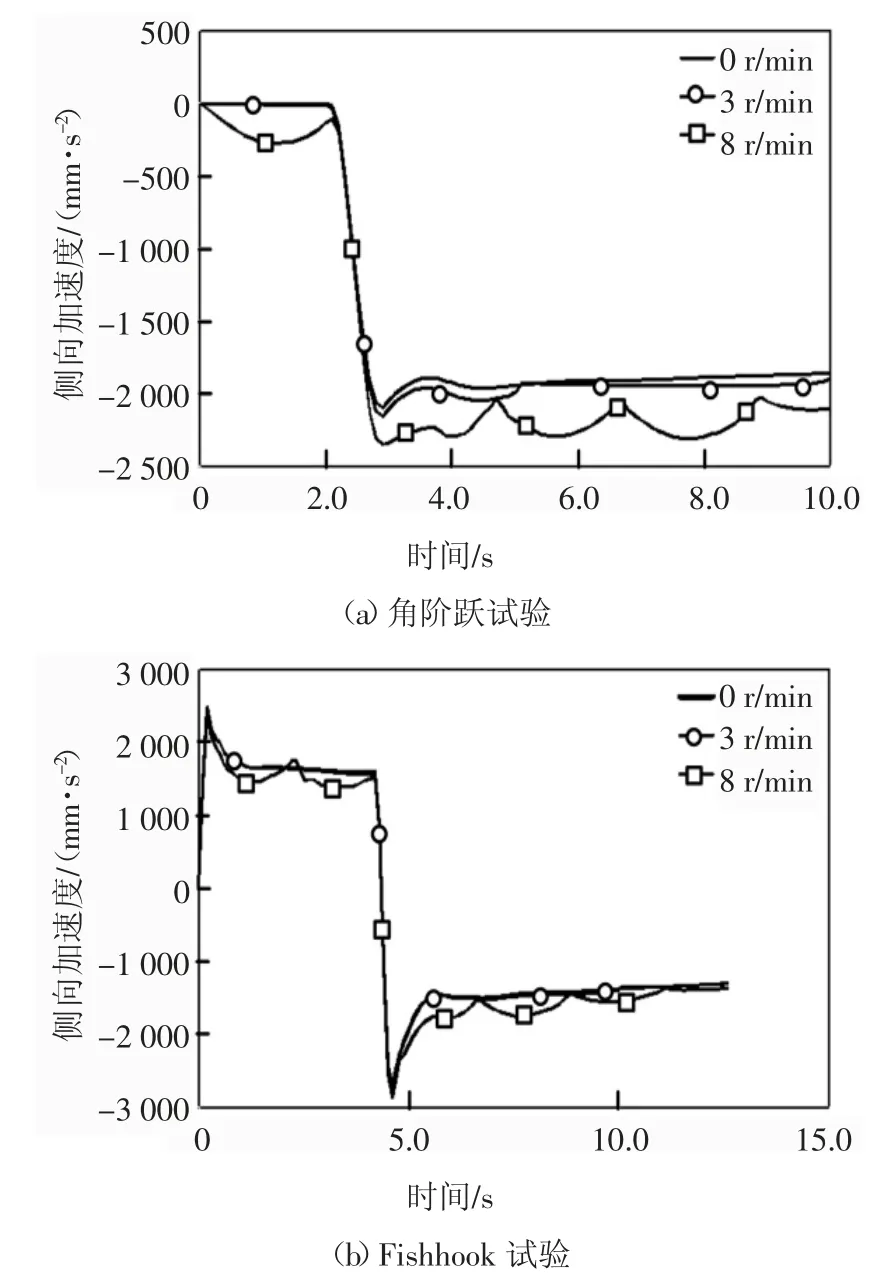
图5 侧向加速度Fig.5 Lateral acceleration

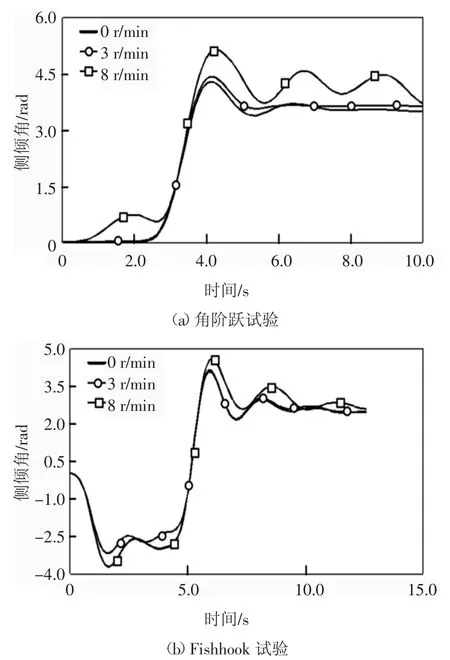
图6 侧倾角度Fig.6 Roll angle

图7 行驶轨迹Fig.7 Traveling track

3 考虑搅拌筒质心动态变化的搅拌车抗侧翻控制

3.1 侧翻评价指标

目前应用广泛的侧翻评价指标大致可分为基于静态门限值和动态门限值两类.前者主要通过分析车辆的侧向加速度、侧倾角等静态参数进行侧翻预测；后者则需要考虑车辆动力学特性，且具有实时性，大部分都是以动态门限值横向载荷转移率为侧翻评价指标.考虑到侧翻检测的准确性和精度，以横向载荷转移率为侧翻评价指标，定义如式（9）所示.

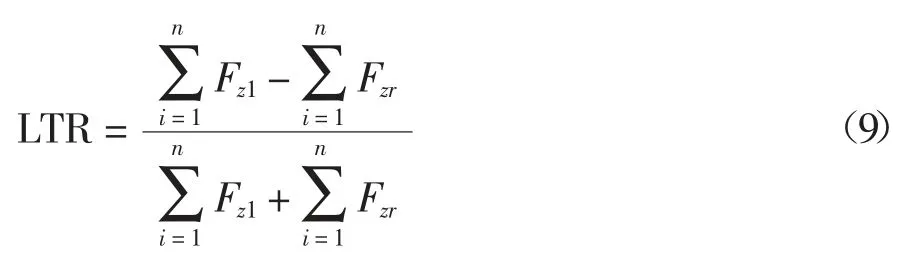
式中：LTR 为横向载荷转移率，Fz1为车辆的第i 桥左边车轮的垂直载荷，Fzr为车辆的第i 桥右边车轮的垂直载荷，n 为车桥的总数.

角阶跃试验，Fishhook 试验工况下考虑搅拌筒动态质心影响的临界侧翻车速分别是58 km/h 和55 km/h，实测横向载荷转移率的结果如图8 所示，由图8 可知，在不考虑搅拌筒动态质心影响时，搅拌车没有达到临界侧翻状态，角阶跃试验工况横向载荷转移率最大值是0.87，Fishhook 试验工况下最大值0.796，最小值-0.726.结果表明，搅拌筒动态运转对搅拌车的侧翻稳定性影响较大.

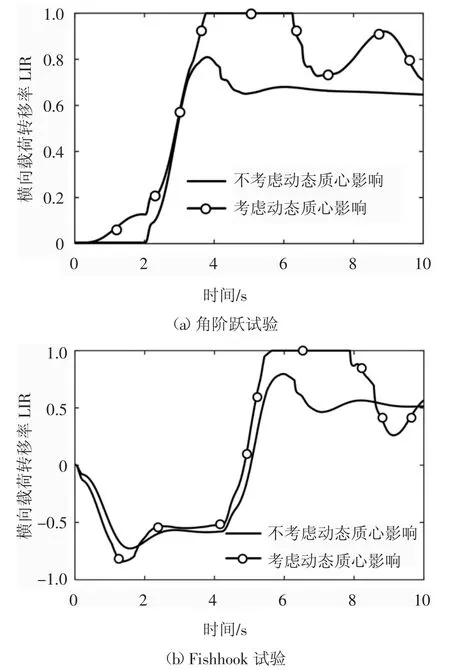
图8 不同试验工况下考虑与不考虑动态质心影响的LTRFig.8 LTR with and without considering the influence ofdynamic centroid under different test conditions

3.2 改进粒子群算法参数整定优化PID 控制系统

粒子群优化算法（Particle Swarm Optimization 简称PSO）是由Eberhart 和Kennedy 提出的一种进化计算技术，源于对鸟群捕食的行为研究.该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型.粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解[28].

实际应用中，PSO 的基本思想是首先进行初始化，得到一群随机的粒子（随机解）.进而，经过多次迭代计算获得问题的最优解.计算过程中的每一次迭代，粒子都会通过跟踪到的个体极值（Personal best）和全局极值（Global best），以式（10）、式（11）为依据进行速度和位置的更新.如图9 所示，基本粒子群算法流程.

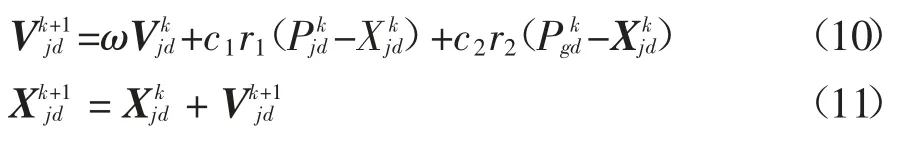
式中：粒子j 在d 维空间里的位置用矢量表示Xjd，飞行速度矢量表示Vjd，ω 为权重因子，r1、r2是介于（0，1）之间的随机数，c1、c2是学习因子，Pjd、Pgd分别是个体极值和全局极值，k 是迭代次数.

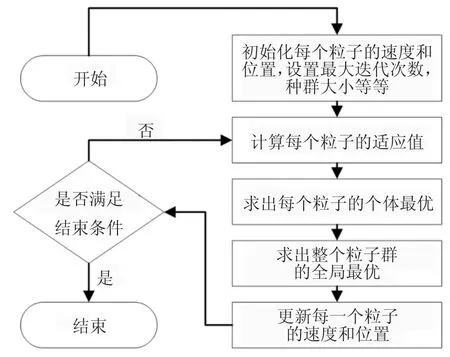
图9 粒子群算法流程Fig.9 The process of particle swarm algorithm

之前的研究表明，惯性权重ω 越大，粒子飞行速度越大，粒子将会以更长的步长进行全局搜索；ω 较小，则粒子步长小，趋向于精细的局部搜索；因此，学者们期望寻找到一个动态变化的ω 值，如式（12）、式（13）所示，使算法在初期的随机搜索中具有较强的全局搜索能力，随着迭代次数的变化，算法后期具有较强的局部搜索能力，使算法在更短时间内寻找到全局最优.但是，式（12）的权值是线性变化的，缺乏动态的变化速率，使得分配在全局和局部搜索能力较强的迭代次数基本一样.因此，在寻找全局最优值和对其逼近的时候比较困难.式（13）表示的权值在前期变化速率太大，很可能导致全局搜索迭代次数太少而寻优陷入局部极值.经过验证，这两种方式在应用时比较困难.

考虑到以上提到的问题、系统的自身特点，以及粒子群算法容易陷入局部最优的缺点，提出一种服从标准正态分布的惯性权重，如式（14）所示，从一定程度上增强算法的全局寻优能力和局部寻优能力，当算法陷入局部最优时，能及时修正，减少找到最优解的迭代次数.

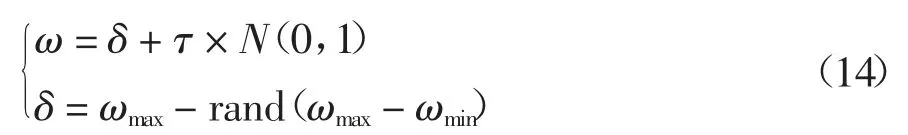
式中：ωmax=0.9，ωmin=0.4，τ=0.5，k 是迭代次数，rand是（0，1）之间的随机数，kmax是最大迭代次数，N（0，1）标准正态分布.

改进粒子群算法参数自整定PID 控制原理图如图10 所示，一方面，自整定PID 算法根据目标参数偏差输入的大小决定输出电压的大小给差动制动系统中的电子机械制动子系统以产生轮胎制动力；另一方面，改进的智能算法通过性能评价指标对控制效果的实时监控，不断迭代后获得最优的一组PID控制参数KP、Ki、Kd.改进的与传统的粒子群算法应用到系统寻优中去，结果如图11 所示，传统算法和改进的算法最优迭代次数分别是63 次、42 次，后者迭代次数减少33.3%，最优结果也很准确，具有较大的优势.

图10 系统控制原理图Fig.10 System control schematic diagram

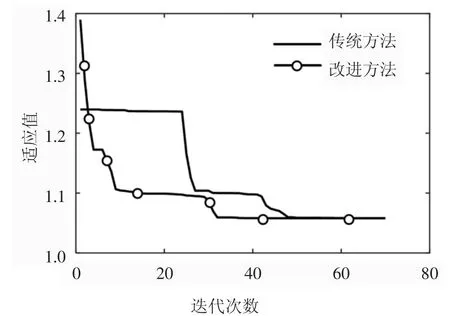
图11 最优个体适应值Fig.11 Optimal individual adaptation

4 侧翻控制仿真分析

联合仿真控制系统如图12 所示，控制系统以横向载荷率为控制目标，自整定PID 根据目标参数偏差输入的大小决定输出电压的大小.基于差动制动理论，当搅拌车因不足转向发生侧翻时，对二、三桥内轮施加制动力；当搅拌车因过多转向发生侧翻时，对一桥外轮施加制动力.判断模块选择制动车轮，根据电压的值，电子机械制动系统产生车轮制动力矩.侧翻控制系统实时计算LTR，当LTR 大于0.8，进行防侧翻控制；当LTR 不大于0.8，自整定PID 输出的电压不会作用于差动制动系统.

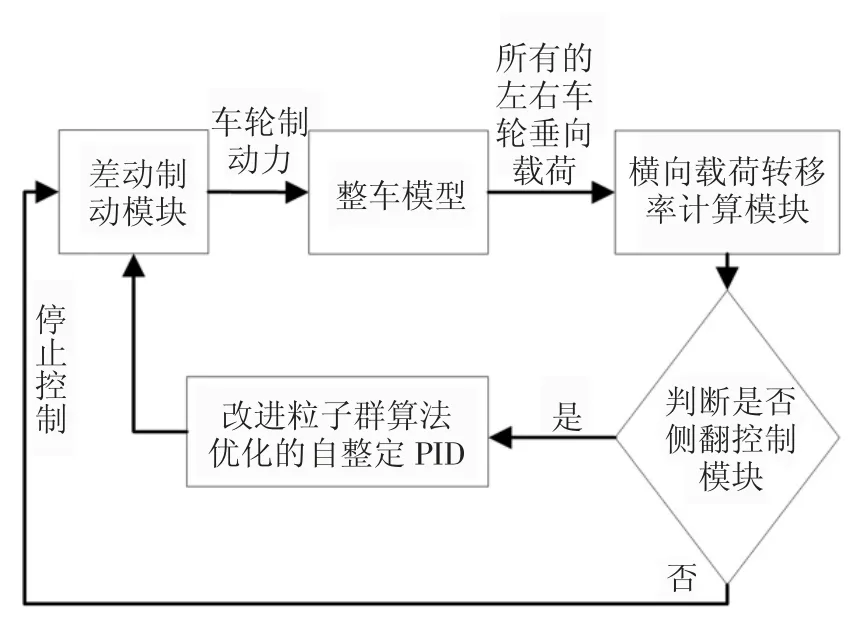
图12 联合仿真控制系统Fig.12 Co-simulation control system

抗侧翻控制仿真分析得到的侧倾角和横向载荷转移率随时间变化的曲线图分别如图13、图14 所示，由图可知，对比未加控制、传统的PID 控制方法、改进的PID 控制方法三次联合仿真结果，角阶跃试验工况，侧倾角、横向载荷转移率的最大值分别是7.98°、6.2°、5.6°和1、0.994 7、0.88；Fishhook 试验工况，侧倾角、横向载荷转移率的最大值分别是11.87°、11.16°、8.72°和1、0.98、0.89.抗侧翻控制系统的作用下，搅拌车的侧翻稳定性都得到了一定程度的提高，使抗侧翻控制系统的有效性得到验证.

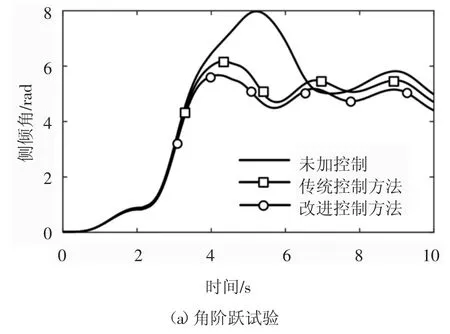
图13 侧倾角仿真结果对比Fig.13 Comparison of simulation results of roll angle

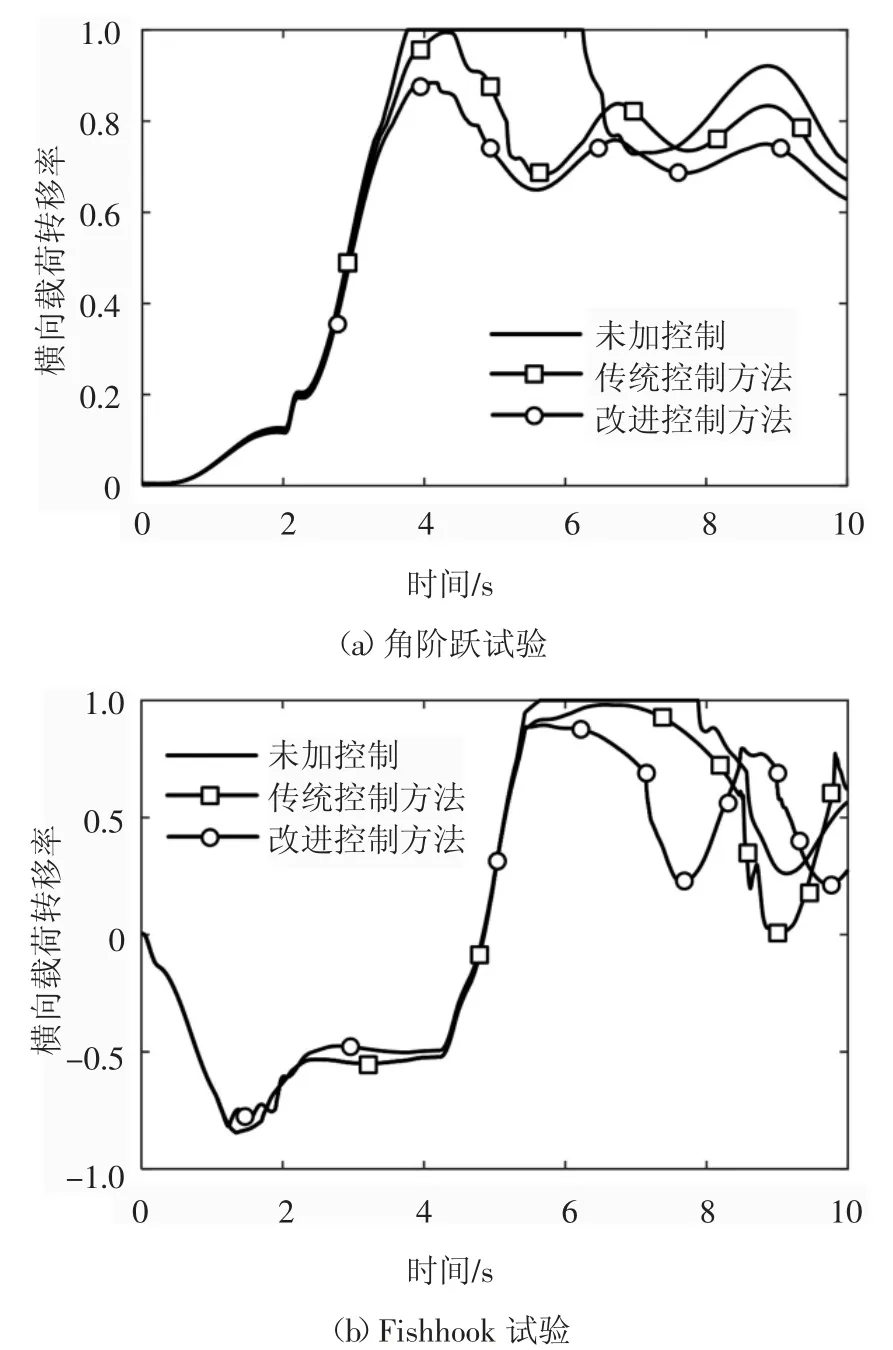
图14 横向载荷转移率仿真结果对比Fig.14 Comparison of simulation results of lateral load transfer rate

5 结论

以提高搅拌车的侧翻稳定性为目标，深入探索了在搅拌车运输过程中，搅拌筒质心的动态变化，基于离散元法建立了搅拌筒动态质心数学模型.建立搅拌筒动态质心的位置变化与搅拌筒支承力的关系，利用函数加载到多体动力学整车模型仿真中，分析其对搅拌车侧翻稳定性的影响.进一步以差动制动理论为基础，设计了传统PID 控制器与改进智能优化算法融合的抗侧翻控制系统.最后，角阶跃和Fishhook 试验工况下，设计的控制系统应用到搅拌车的抗侧翻控制仿真中验证有效性，仿真结果显示，该控制系统在提高搅拌车的抗侧翻稳定性方面有较大的优势.