基于Gamma 和混合Copula 的元动作单元性能可靠性分析
张根保,张定飞,冉琰,应广祺
(重庆大学机械工程学院,重庆 400044)
随着高新技术不断发展和应用,产品(或系统)的高度集成化、高度智能化和复杂性不断提高,并广泛应用于航空航天、核电厂设备和大型工业机器当中,复杂机电产品的可靠性研究逐渐成为可靠性工程领域的关键问题[1-2].性能可靠性研究是产品质量特性研究的一个重要内容,可靠性的优劣直接决定了产品的性能和市场接受程度,因此利用科学合理的评估方法进行可靠性分析在很大程度上可以有效指导产品的设计、开发、制造和维护策略优化等,从而保障和提高产品质量.针对故障信息、性能退化数据和工艺数据等的可靠性分析是如今可靠性研究的主要研究方向[3].基于性能退化数据进行可靠性分析是目前广泛使用的方法之一.产品性能在退化过程中包含着大量与寿命有关的关键信息,所以从产品性能指标变化着手,对性能指标进行连续测量得到相应的退化数据,就可对产品性能的退化过程进行分析,进而评估产品可靠性.
目前,国内外学者针对产品的性能退化过程和可靠性分析方面进行了大量研究工作.在产品性能退化方面,Kim[4]等为了解决产品实时可靠性预测问题,于1992 年首次提出了性能可靠性的概念.Wiener 过程由于其简单的结构和直观的数学表达式而受到广泛应用,已然成为性能退化建模中最为广泛的一种模型.如王玺[5]等针对航空发动机性能衰减过程具有的非线性和不确定性特点,利用非线性Wiener 过程建立同时考虑二者特点的性能衰减模型,进而推导剩余寿命分布.张雄健[6]等利用广义Wiener 过程,提出了一种双时间尺度函数模型来描述航空航天设备常用的组件激光器的退化过程.Zhang[7]等针对复杂系统退化过程中的非线性和随机性,提出了一个与年龄和状态有关的通用非线性退化模型,利用具有与年龄和状态相关的非线性漂移和挥发性系数的扩散过程来表征轴承退化过程的动态性和非线性.其它性能退化模型也有大量的研究,如Wang[8]等假设一个产品具有两种性能特征,两种性能特征相互依赖,依赖关系通过一个Copula 函数来表征,同时每种性能特征的退化遵循非平稳的伽马退化过程,利用贝叶斯方法实时更新随机效应来描述性能退化过程.Duan[9]等针对设备退化数据实际组成特点,提出一种面向不同类型小样本数据的可靠性评估方法,引入最小二乘支持向量机(LS-SVM)回归算法分析设备性能退化过程,实现系统性能联合可靠性的计算,并将其应用于特定类型的CNC 机床.在可靠性研究方面,主要涉及可靠性分析方法与建模.周伟[10]等针对元动作单元之间的相互作用所引起的性能依赖会给多态系统可靠性造成影响,给出了非齐次马尔可夫模型,分析并确定了元动作单元的多状态演变过程以及多态单元处于各状态的概率,利用向量通用发生函数建立了可靠性分析模型.鞠萍华[11]等为解决可靠性研究中分析数据不足的问题,提出一种基于模糊物元法的相似元动作单元提取方法,利用相似元动作单元为元动作单元的可靠性分析提供充分的寿命失效数据,最后通过三参数威布尔分布进行建模和可靠性分析.张根保[12]等在元动作理论的基础上进一步给出元动作链理论,将产品微观失效原因和运行信息纳入考虑,构建宏观系统可靠度与微观元动作运行失效之间的联系,准确应用于机床的故障模式分析,消除了传统可靠性建模过程不确定性问题.Chai[13]等针对机械零件疲劳可靠性分析中存在样本计算量大且忽略概率密度函数信息的问题,利用Kriging 模型构建了学习函数,结合蒙特卡洛模拟,开发了一种新的结构可靠性分析方法.An[14]等针对机械系统中存在复杂相互关系的问题,利用Copula 函数来解决相关性问题,详细研究并建立了串并联机械系统的可靠性模型,得到它们的可靠性函数.以上研究对复杂机电产品的性能退化和可靠性建模、评估、预测起到了重要作用.
然而,复杂机电产品是一个多子系统交叉耦合的整体,其性能退化和可靠性问题涉及内部众多子系统及其零部件和其它影响因素,导致性能退化建模和可靠性分析过程的计算量和复杂程度大大提升,建模工作难以实施[15].机电产品的性能好坏一般体现在其是否能实现所要完成的某一特定功能,因此对实现某一特定功能的元动作单元进行退化建模和可靠性分析,既可以有针对性地对机电产品实施模块化建模,同时也可以降低分析和计算的复杂程度.
为此,本文分析机电产品性能退化过程特点时将其性能与特定功能联系起来,简化其性能退化和可靠性建模分析过程,以实现特定功能的元动作单元的退化过程为分析对象,提出元动作单元的性能可靠性分析通用模型及其建立方法,并以某加工中心的托盘交换架为例,验证所提出的性能可靠性分析通用模型的可行性和有效性.
1 元动作单元和非线性Gamma 随机过程
1.1 性能退化与功能的关系
系统(产品)的性能退化是指性能参数随时间发生的物理或化学变化,性能退化一般过程如图1所示.

图1 性能退化过程Fig.1 Performance degradation process
性能退化到阈值Xfc后,则认为系统失效,功能无法实现.即在性能阈值内,属于性能问题,超过阈值则属于功能问题.复杂机电产品存在多种子系统耦合现象,单纯的进行性能可靠性分析固然是困难的.然而产品是以实现其各种功能为目的而存在的,不同功能对应不同的子系统去完成,因此,我们可以将产品性能可靠性研究问题转化为研究实现特定功能的对象的性能可靠性,进而简化性能可靠性建模和分析过程.
1.2 元动作和元动作单元
对于结构复杂的产品而言,根据文献[16-17]的研究方法,可以利用功能(Function)-运动(Motion)-动作(Action)的功能运动层次分解方法将其功能映射为部件的运动,部件的运动又可以继续分解为实现该运动所需的动作,即实现产品功能的最小运动单元——元动作(Meta-Action,MA),FMA 分解使得可靠性建模和分析过程得到简化.
FMA 分解过程可以总结为:首先研究系统要实现的功能,然后将功能分解为各个子系统(部件)的运动,最后将子系统的运动再分解成动作,即为元动作,如图2 所示.

图2 FMA 分解示意图Fig.2 FMA decomposition schematic
元动作单元的所有相关零件(动力输入件、动力输出件、中间件、支撑件、紧固件)按照装配关系构成的整体称为元动作单元.元动作单元包括移动元动作单元和转动元动作单元两类,移动元动作单元实现最基本的移动功能(直线移动),如油缸中活塞移动单元、齿条移动单元等;转动类单元实现最基本的转动功能(定轴转动),如齿轮转动单元、丝杠转动单元等.元动作链是指按照某种运动流组合在一起的、用以完成某一预定运动的元动作序列.其建立对象是一个单一的运动传递关系,如图2 中实现运动M221的动作层A 中的元动作M2211向M221t传递的路径.
1.3 单个零件性能退化及非线性Gamma 随机过程
往往一件产品可以分解得到多种元动作单元,从而将产品的性能退化映射为元动作单元的性能退化.然而并不是所有元动作单元都会产生性能退化趋势,对于存在性能退化趋势的元动作单元而言,主要考虑其内部单个零件受到磨损、腐蚀、疲劳、老化等形式的物理劣化,其性能退化量不断累积.然而维纳过程并不能很好地描述磨损和累积损伤,因此我们使用具有单调性质的Gamma 过程建立随机退化模型来描述单元中的零件性能退化过程[18],趋势如图1 所示.
单个零件的退化也是一个多维性能指标共同作用表征的结果,因此在分析之前,给出单个零件的多维性能退化指标转化为一维的性能退化指标的数据融合公式[19],即性能退化量.融合公式为

式中:xi(t)为第i 个零件的性能退化量;xik(t)为第i个零件在t 时刻第k 维性能指标退化值;xikf为零件i 的第k 维性能指标独立发生失效时的退化值;为零件i 的k 维性能指标独立发生失效时的退化平均值.
非线性Gamma 过程对磨损过程具有良好的分析能力,假设单个零件的性能退化服从非线性Gamma 分布,记随机变量服从形状参数为α >0,尺度参数β >0 的非线性Gamma 分布,则其概率密度函数为:
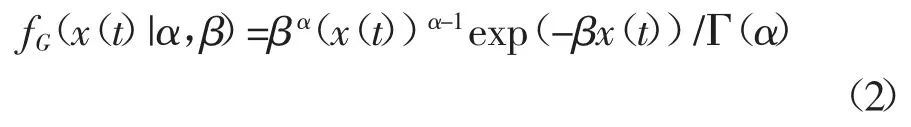
式中:fG(x(t)|α,β为伽马概率密度函数,α 和β 分别为分布的形状和尺度参数,Γ(α)=为Gamma 函数.
上述Gamma 过程具有如下性质:
1)对于任意时刻,x(t+Δt)-x(t)~Ga[αΔt,β]成立;
2)退化速率是平稳的,x(t)具有独立的增量;
3)在t=0 时,x(t)的退化被认为是零.
形状参数α 描述的是外部环境等因素对元动作单元性能水平的影响,而尺度参数β 描述的是随机性因素(振动、冲击)对元动作单元性能水平的影响.为了方便研究,本文在建立退化模型时不对随机因素的影响进行考虑,因此,我们假设形状参数与时间相关,即α=at.则x(t)在时间t 处的均值和方差可以分别表示为:

则性能退化量x(t)的概率密度函数表示为:
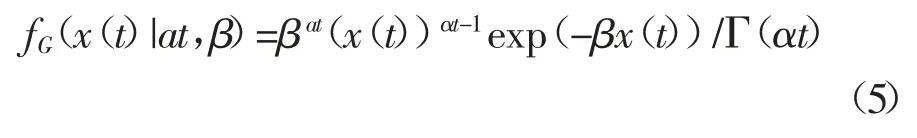
x(t)的累积分布fG(x(t)|at,β)可以使用不完整的伽玛函数进行评估.根据图1 中单个零件的失效时间T 为x(t)首次达到或超过Xfc的时间,即

则元动作单元性能退化的累积分布函数可以表示为:

1.4 模型参数的点估计
本文采用矩估计法对非线性Gamma 随机过程模型进行参数估计.复杂产品往往具有高可靠和长寿命的特点.因此,实际中一般采用离散、长间隔且非周期性的状态监测方法,造成单元中每个零件的监测次数非常有限.为了能获取足够的监测数据进行参数估计,我们假设同类单元内相同类型零件表现出相似的性能退化机理.因此,可利用多个同类单元中同类型零件的性能退化数据用于参数估计.
假设系统有N 个同类型零件,在时刻t1,t2,…,tm分别对各零件进行m 次监测,记对第i 个同类零件进行第j 次监测的时刻为ti,j,监测值转化后的性能退化量为X(ti,j),得到第i 个同类型零件的性能退化量矩阵为:

那么第i 个同类型零件在时刻ti,j和ti,j-1之间的退化量Δxij可以表示为:

则退化量的样本均值为
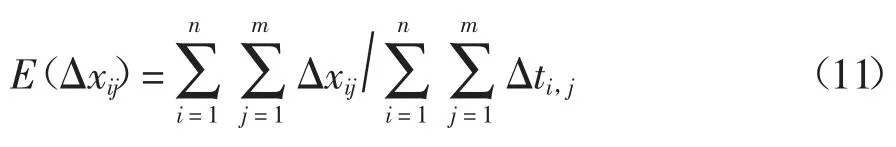
通过Gamma 函数的均值构造函数M=Δxij-Δti,j,因此由Gamma 性质可知E(M)=0,可得
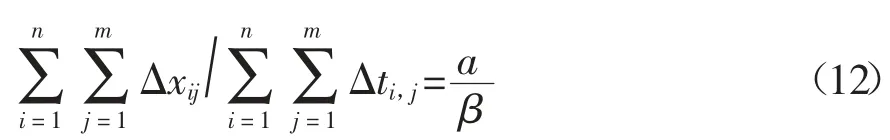
退化量的样本方差为

则对构造函数M 进行变换,化简后可得:
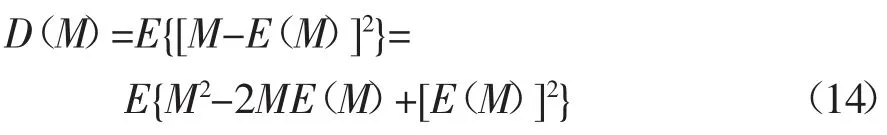
由于E(M)=0,化简后可得
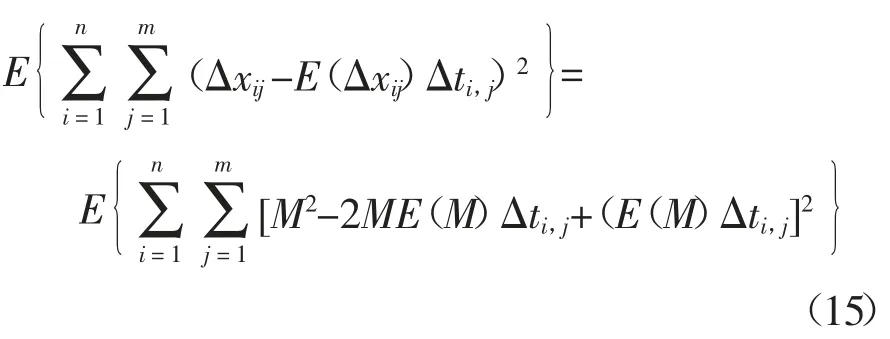
最后通过计算可得

利用数值计算方法求解式(12)和(16)构成的方程组,即可得到参数a 和β 的估计值.
2 基于Copula 函数的元动作单元性能可靠性建模
2.1 元动作单元内部结构及其性能水平
在复杂产品中,任何一个单独的零件都不能孤立地完成一个动作,即单个零件本身是没有功能的.任何一个元动作的实现都需要其他零件的协助,即一个元动作单元完成其动作是由其内部所有零件共同完成的,这些零件共同构成一个最基本的结构单元,共同实现一个元动作.根据元动作单元的结构组成要素及装配关系,给出其概念示意图及内部结构关系,如图3 所示.
组成元动作单元的五大要素定义分别如下[20]:输入件:为元动作件提供运动和动力或接收上游元动作单元输出的运动和动力的零件.
输出件:元动作单元中,向下游元动作单元输出运动和动力的零件.
中间件:元动作单元中,起传递运动和动力作用,并使输入件和输出件保持正确位置的零件.
紧固件:元动作单元中,起固定、防松和密封作用、或用来连接多个零件、且相互间没有相对运动的零件.
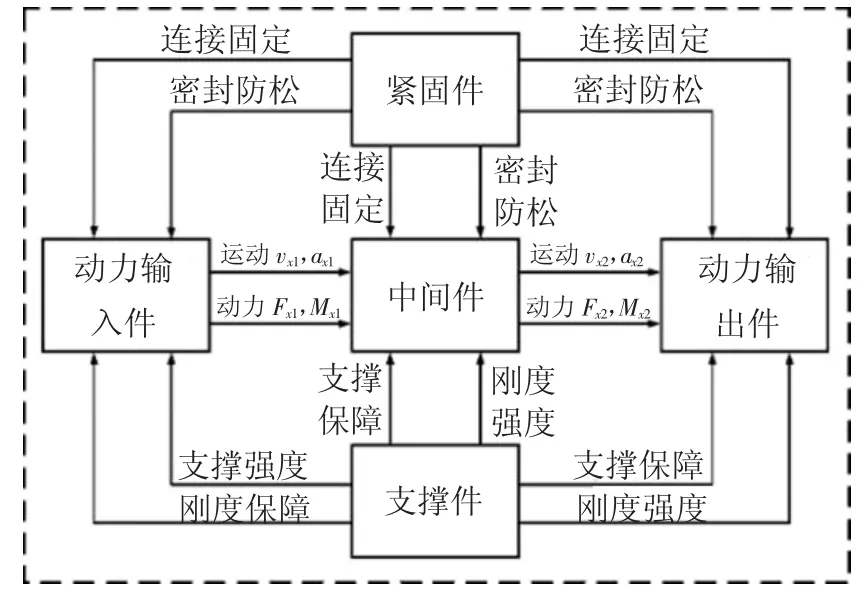
图3 元动作单元结构示意图Fig.3 schematic diagram of unit structure
支撑件:元动作单元中,用来作为其他零件安装基准的零件.
元动作单元的性能水平定义为完成某一预定动作的元动作单元在服役过程中内部结构零件发生依赖耦合后所表征的整体性能退化量.元动作单元内部结构之间的依赖耦合关系,其性能退化量一定存在着复杂的非线性变化.假设一个元动作单元含有m 个必要零件,y1(t),y2(t),…,ym(t)表示t 时刻内部各零件的性能退化量,F1(y1),F2(y2),…,Fm(ym)表示对应零件的累积失效分布函数.定义元动作单元性能的累积分布函数FMA,他们应具有如下关系,即存在某一函数关系使得下式成立.
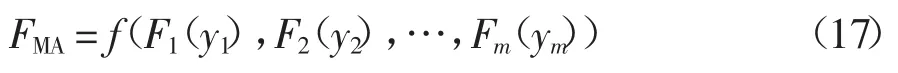
其中f(·)是未知的函数关系.
2.2 Copula 函数
设有随机变量X=(x1,x2,…,xn),其联合分布F1(x1),F2(x2),…,Fn(xn),且当F1(x1),F2(x2),…,Fn(xn)连续时,对于n 维随机变量存在唯一的n 维Copula函数,使得下式成立
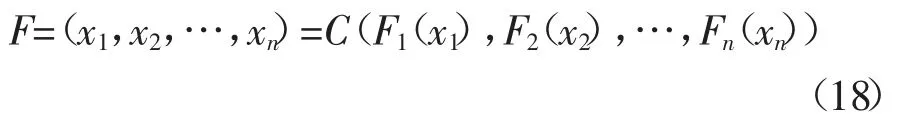
可以看出,n 维随机变量x 的联合分布函数可以用一个Copula 函数表示,其中所有的一维边际分布函数Fi(xi)都是其变量.也就是说,不同随机变量的相关关系,根据它们的边际分布函数,可以通过一个Copula 函数来体现.
Copula 函数包括正态Copula 函数、T-Copula 函数以及阿基米德Copula 函数.其中阿基米德Copula函数包含常用的Gumbel-Copula、Clayton-Copula、Frank-Copula 三种函数.
2.3 基于Copula 的元动作单元可靠性模型
Copula 函数可用于表征一组随机变量与边际分布函数的依存关系,在简化具有依存关系结构的联合概率分布的分配方面具有很好的表现[21].因此本文通过Copula 函数考虑元动作单元内部结构的依赖耦合关系.类似地,在元动作单元的性能可靠性分析中,包含相同随机退化过程的不同类型零件之间的依赖耦合关系也可以通过Copula 函数来体现.在本文研究中,Copula 函数中讨论的随机变量xi(或时间t 的随机过程xi(t))表示元动作单元内部第i 个类型零件的性能退化量(或第i 个类型零件的连续磨损,疲劳等)或者是累积失效分布函数.
这里引入串联系统的概念[22],当系统中任一构件失效而造成系统失效则为串联系统,反之则为并联系统.元动作单元内部只要存在一个必要零件发生失效,则认为元动作单元功能不能正常发挥,因此本文认为元动作单元属于串联系统的一种形式.
假设元动作单元内第i 个必要零件的累积分布函数为FGi,则元动作单元的累积失效分布函数为

式中:FMA是元动作单元的累积失效分布函数;C2(·),C3(·),…,Cm(·)是Copula 函数,表示元动作单元内部同时有(2,3,…,m)个零件发生依赖耦合退化.
则考虑依赖耦合的元动作单元可靠度为

3 基于混合Copula 函数的元动作单元性能可靠性建模
3.1 混合Copula 函数
元动作单元内部结构之间依赖关系造成其性能退化量存在着更为复杂的非线性变化,单一的Copula 函数只能反映某一种特定的非线性变量之间的相关性或非对称结构.研究表明混合Copula 函数比单一的Copula 函数更能准确的反映非线性变量之间的相关性与非对称结构[23].
混合Copula 函数是利用多种Copula 函数乘以权重系数进行叠加,因此能够更加全面的表征随机变量的分布特性.其数学表达式如下:
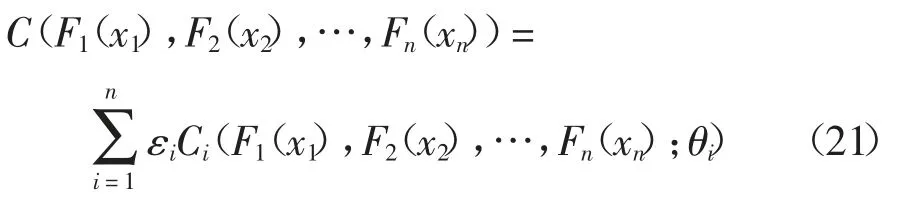
为了研究方便起见:选取三种最优Copula 函数构造一个混合Copula 函数.

式中:C1(·θ1)、C2(·θ2)、C3(·θ3)分别为提取出的3 种最优Copula 函数;θ1、θ2、θ3分别为对应的相关参数,反映了各变量间的相关程度;εi为权重系数,描述了各变量间的相关模式,且有:ε1+ε2+…+εn=1,可以通过改变权重系数εi,使得混合Copula 函数能够更好地表征变量之间的对称性与非对称性结构.
3.2 混合Copula 函数相关性度量指标及最优选择
我们选择应用较为广泛的二元Copula 函数进行简单特征分析并结合其他模型判断准则,给出三步方法提取出几种最优的Copula 函数构造混合Copula 函数用于元动作单元的性能可靠性建模.
假设二元Copula 函数为C=C(m,n),m=F(x1),n=F(x2),相关性度量指标及函数选择具体方法如下:
1)散点图法:通过绘制任意两组原始数据的散点图,观察退化数据是否成对称分布,以及上尾部和下尾部的变化情况.同时对比几种常用Copula 函数的特征可以大致选择一种或几种合适的Copula函数.
上下尾部的变化情况可由尾部相关系数进行度量.假设任意两个随机变量x1、x2对应的边缘分布函数分别为m=F(x1)和n=F(x2),两随机变量的上下尾部相关系数分别定义为[24]:

若λup∈(0,1],则称两随机变量x1、x2为上尾部相关,若λup=0,则称为上尾部独立;反之,λlow∈(0,1],则称两随机变量x1、x2为上尾部相关,若λlow=0,则称为下尾部独立.
根据二元Copula 函数的性质,尾部相关系数可以通过Copula 函数进行表示.
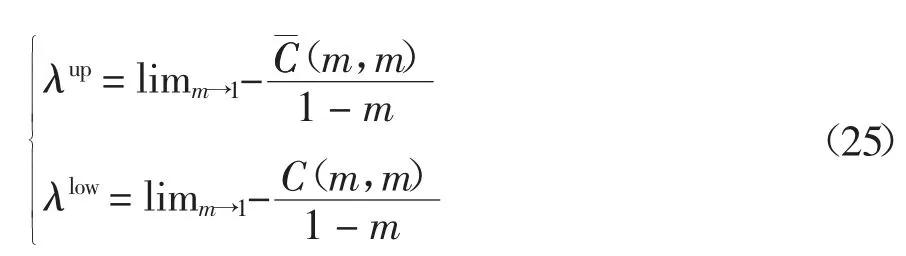
2)秩相关系数检验法:原始退化量之间的相关系数,并不能很好地表现单调不变性,因此选用Kendall 秩相关系数τ 来弥补相关系数的不足,再通过与常用Copula 函数的Kendall 秩相关系数进行对比,选择更接近的Copula 函数.
Kendall 秩相关系数τ 与各Copula 函数之间存在一定的转换关系,可通过散点图的绘制分析得出或计算Copula 函数参数得到,转换关系如表1 所示.

表1 转换关系Tab.1 Conversion relationships
其中:ρ、α 为各Copula 函数的模型参数;Dm(x)=
3)赤池信息准则(AIC):AIC 准则适用于通过极大似然估计法得到的参数估计模型.

式中:k 表示Copula 模型中参数个数,log(MLE)是整体对数似然函数值.如果计算的AIC 值越小,说明模型的拟合程度更高,并且在似然函数差异性不显著时,模型的复杂度越低.
若对于统计样本是离散型的,则可以将赤池信息准则进行转换得到式(28).

式中:n 代表观察样本数量,RSS 为剩余平方和.
通过上述三步法可以合理选出最优Copula 函数用来构造混合Copula 函数.
3.3 混合Copula 函数参数估计
参数估计的方法主要有极大似然估计法(MLE),最大期望值(EM)、贝叶斯线性回归和两步参数估计法.考虑数据处理的精确性并防止过拟合现象,本文采用蒙特卡罗方法产生随机样本数据,并基于最小偏差平方准则,通过改进的遗传算法优化求解混合Copula 函数的未知参数估计问题.
采用蒙特卡洛模拟方法,对系统中每个零件的随机变量进行采样.将采样的随机数据代入对应于各零件失效退化的函数中.每个函数生成与采样数据对应的性能退化量序列x(t).将每个性能退化量序列x(t)转化为相应的累积分布函数FG(x(t)).
遗传算法作为一种自适应型全局优化搜索算法,具有很强的适应性,在组合优化等方面得到了广泛的应用.遗传算法的基本思想为:从问题的潜在解集的其中任意一个种群开始,种群则由二进制编码形式构成的一定数目的个体组成.父代由初代种群组成,计算每个个体的适应度值,并保留m 个精英个体,进行选择、父代交叉、个体变异操作后,判断是否满足适应度条件,若不满足则继续执行交叉、变异操作,判断子代种群是否满足算法结束要求,不满足,则以新的种群作为父代,重复上述步骤,直到满足计算要求为止.本文利用改进的多目标遗传算法对混合Copula 函数的未知参数进行优化求解,具体步骤及流程图如图4 所示.
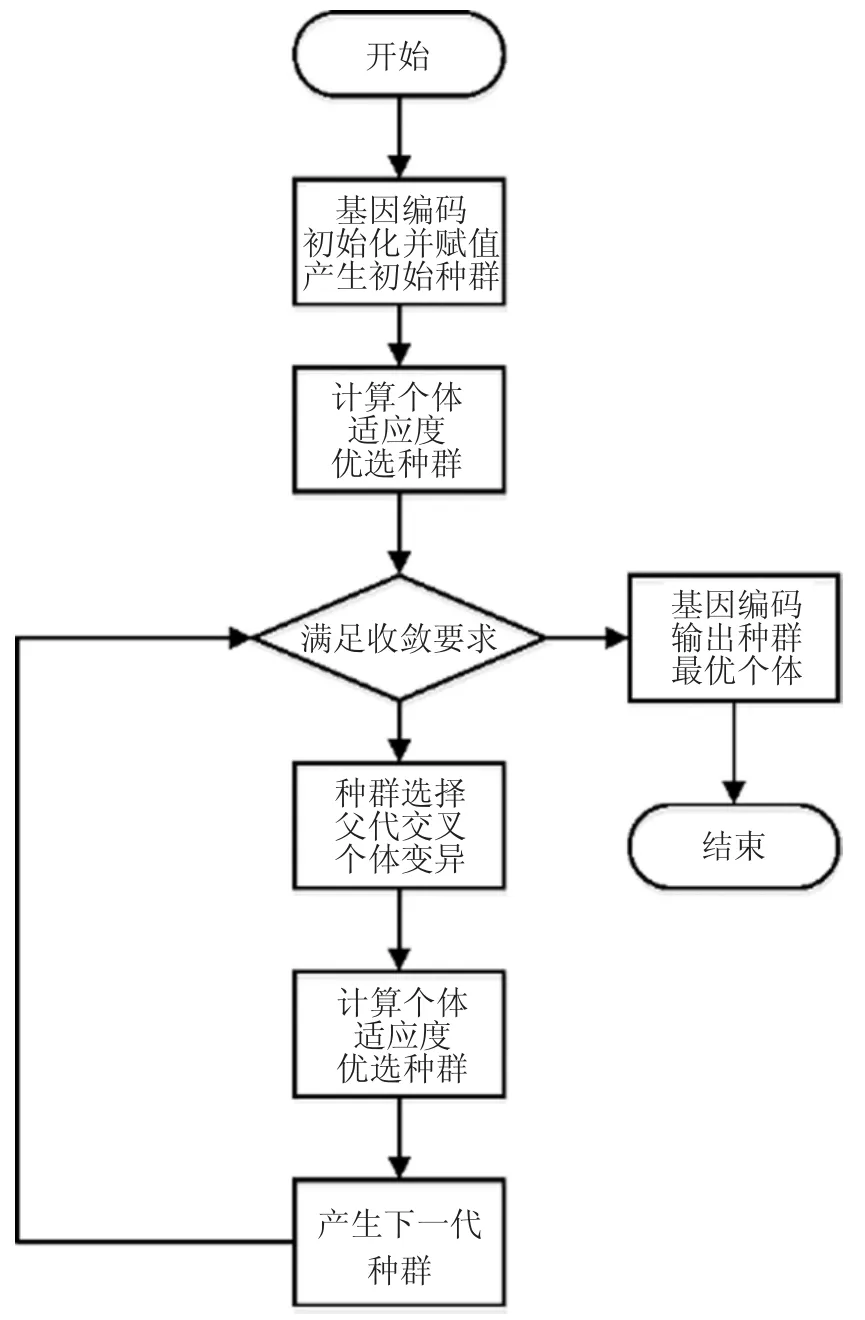
图4 改进的遗传算法流程图Fig.4 Improved genetic algorithm flow chart
1)编码、参数初始化
使用二进制编码将采样数据转换成二进制串形式

式中:amam-1…a2a1代表实数的整数部分,bnbn-1…b2b1代表实数的小数部分.
参数包括种群规模N、交叉概率Pc、变异概率PM、进化代数T,编码精度R.当种群规模N 太小时,会出现近亲交配,产生病态基因;种群规模较大,难以收敛,稳健性下降.一般取0~100.交叉概率Pc是更新种群的重要方式,交配概率太大破坏已有的有利模式,随机性增大,容易错失最优个体;交配概率太小不能有效更新种群,一般取0.4~0.99.变异概率PM太小时,种群的多样性下降太快,导致有效基因的迅速丢失且不容易修补;当变异概率太大时,高阶模式被破坏的概率随之增大.一般取0.000 1~2.进化代数T 太小,算法不容易收敛,种群还没有成熟;代数太大,进化没有意义,浪费时间和资源.一般取100~500.编码精度R 为遗传算法的停止准则.
2)遗传算子
包括选择、交叉、变异.选择操作的任务就是按某种方法从父代群体中选取一些个体,遗传到下一代群体.这里使用比例选择算子,即各个个体被选中的概率与其适应度函数值大小成正比.设群体大小为n,个体i 的适应度为Fi,则个体i 被选中遗传到下一代群体的概率为:

每个概率值组成一个区域,全部概率值之和为1;最后再产生一个0~1 之间的随机数,依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数.交叉操作以某一概率相互交换随机搭配的某两个个体之间的部分二进制串,包括单点交叉、两点/多点交叉,部分序列交叉等,本文采用多点交叉.变异操作是对个体的某一个或某一些二进制串按某一较小的概率进行取反操作,本文采用两点变异.
3)改进的适应度函数
适应度是遗传算法终止的停止准则.本文采用在均方根误差公式的基础上加入惩罚项作为混合Copula 函数未知参数估计优化求解的适应度函数.RMSE 公式如下:
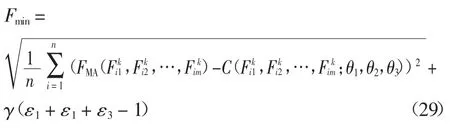
式中:FMA为累积分布函数序列是混合Copula 函数,γ 为惩罚因子.当适应度满足编码精度的条件时,则输出对应的二进制串,最后通过解码公式得出十进制的混合Copula 的未知参数
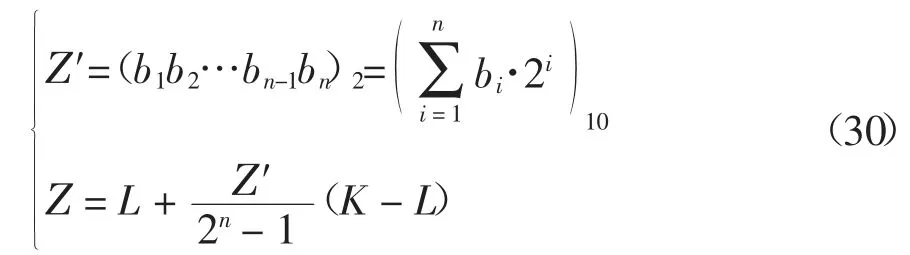
式中:Z 代表实数;L、K 分别代表未知参数定义域区间的两个端点.
这种方法可以使搜索区域分布在整个搜索空间,提高种群的遍历性,可以更好地跳出局部最优解.
将求解出的参数代入式(20)(21)和(23)即可得到基于混合Copula 的元动作单元性能可靠度表达式.
4 应用实例
以某加工中心切削辅助功能中的托盘交换架交换工件运动为例,首先按FMA 分解托盘交换架,得到动作层各个元动作,如图5 所示.

图5 托盘交换架结构化分解模型Fig.5 Pallet exchange rack structural decomposition model
提取交换架回转运动M112中的齿轮转动元动作单元A1124作为本次实例分析的对象,其内部结构图如图6 所示.
在齿轮转动元动作单元的五大组成要素零件上安装多类传感器,其中输入件、输出件和中间件均属于转动零件,选用加速度传感器,温度传感器,支撑件和紧固件均属于固定型零件,选用位移传感器,设定间隔时间并进行性能指标数据监测,监测的性能指标主要包括振动信号,磨损量,重复定位精度,工作温度等,分析得到齿轮转动元动作单元内部每个组成要素零件的多组性能退化数据.利用式(1)将多维性能退化数据融合为单个零件的性能退化量,再将其与设定的间隔时间代入式(10)(12)和(16),求得元动作单元内部各类型零件的Gamma 参数估计值,如表2 所示.
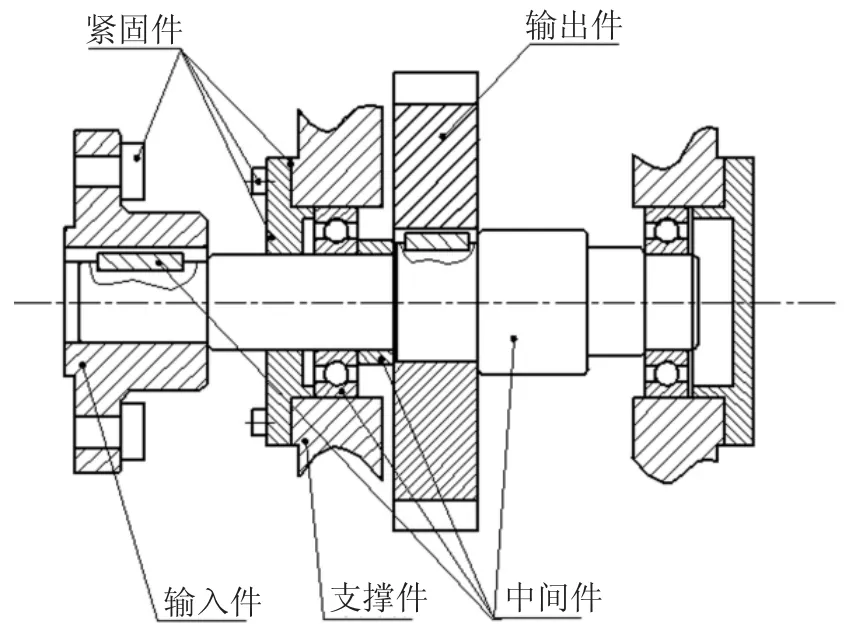
图6 齿轮转动元动作单元的结构模型Fig.6 Gear rotation meta action unit structural model

图7 元动作单元五大件的可靠度曲线Fig.7 Meta action units five types components reliability curve

表2 参数估计结果Tab.2 Parameter estimation results
联合各参数估计值和式(7)(8)推导出元动作单元内每个类型零件的可靠度曲线,如图7 所示.
从图7 可以看出,元动作单元内部各零件的可靠度曲线随元动作单元服役时间的延长,其内部结构之间的挤压、摩擦不断作用各组成要素,导致各零件不断出现磨损、蠕变和疲劳等退化现象,性能退化量不断增大,可靠度不断下降.这也标志着元动作单元内部结构老化程度逐渐增加.各类零件的可靠度曲线的平滑程度不一,即在同样的时刻下,各零件的可靠度水平不同,如果选用最弱环节理论来评估元动作单元的可靠性则会高估元动作单元的性能可靠性水平,若认为元动作单元内各类型零件退化过程独立,则会低估元动作单元的性能可靠性水平.
因此通过考虑元动作单元内部结构的依赖耦合分析元动作单元的性能可靠性水平,利用本文所述的3 种方法提取3 种最优的Copula 函数构造混合Copula 函数,采用10 个齿轮转动元动作单元的10个观测时刻对应下的各组成要素的多种性能指标样本值,利用公式(1)计算分别得到对应时刻下各同类组成要素共100 个性能退化量数值,其中元动作单元内的动力输入件和动力输出件的退化量失效阈值为14,中间件、紧固件和支撑件的退化量失效阈值为20,挑选任意两种类型零件构造一系列二维散点图,结果如图8 所示.

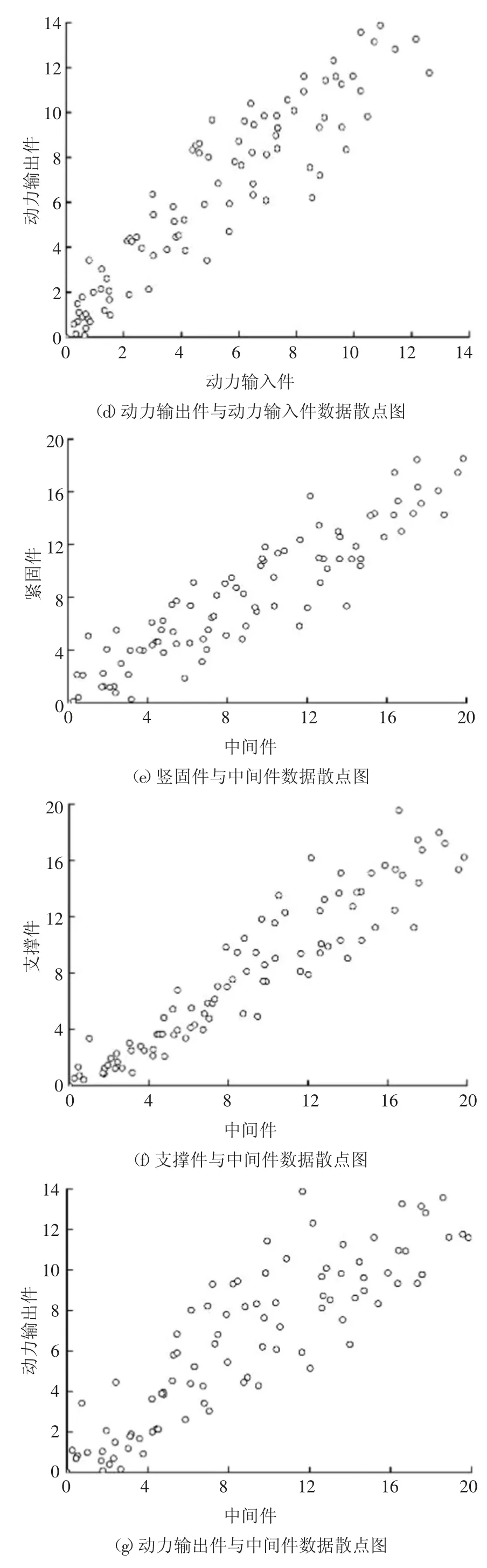

图8 元动作单元各零件之间的相关关系图Fig.8 Different parts scatter diagram in meta action unit
同时计算各零件性能退化量的Kendall 相关系数,相关系数矩阵结果如表3 所示.
各类Copula 函数的相关系数如表4 所示.
结合样本数据和上述计算时得到的极大似然函数估计值,获得各Copula 函数对应的AIC 值如表5所示.

表3 秩相关系数矩阵Tab.3 Rank correlation coefficient matrix

表4 Copula 函数的秩相关系数Tab.4 Copula function rank correlation coefficient

表5 Copula 函数的AIC 结果Tab.5 AIC results of Copula function
通过二维散点图特征可以发现,元动作单元内部各组成要素零件的性能退化量基本上存在对称分布和下尾部相依关系,上尾部相依关系表现不太明显,表4 中显示除了Gumbel,其余Copula 函数的Kendall 与五大件之间的Kendall 较为接近,进一步证实了散点图表现出的对称和下尾部相依关系.根据AIC 选择理论,Frank、Clayton 和T-Copula 对应的AIC 值相对较小,说明该3 种Copula 函数用于描述样本数据可以获得更为准确的结果,因此将它们作为3 种最优Copula 函数用于构造混合Copula 函数.最后利用本文提出的改进的遗传算法优化求解混合Copula 参数估计,结果如表6 所示

表6 混合Copula 函数的参数估计结果Tab.6 Parameter estimation results of mixed copula
将参数估计结果代入式(19),结合(20)和(22),得到混合Copula 函数的可靠度表达式,下面选取元动作单元内部两种类型零件并通过混合Copula 函数考虑两者之间的依赖耦合关系,得到的元动作单元性能可靠度曲线,如图9 所示.

图9 齿轮转动元动作单元可靠度曲线对比Fig.9 Comparison of reliability curves of gear rotating element action unit
从图9 中可以看出通过混合Copula 函数得到的齿轮转动元动作单元的可靠度曲线介于最弱理论和独立假设之间,可以得出较为科学、准确的可靠度变化结果,具有良好的适用性,也证明了本文方法用于分析元动作单元性能可靠性水平的有效性.
考虑产品功能的实现可能与多个有关的元动作单元有关,科学合理的估计产品的可靠性水平,需要同时对多个元动作单元进行可靠性分析,于是我们再次提取交换架回转运动M112中的齿条移动元动作单元A1123作为分析对象,按照相同的操作流程,绘制得到齿条移动元动作单元的可靠度曲线,如图10 所示.

图10 齿条移动元动作单元可靠度曲线对比Fig.10 Comparison of reliability curves of rack moving element action unit
从图10 中可以看出通过混合Copula 函数得到的齿条移动元动作单元的可靠度曲线仍介于最弱理论和独立假设之间,与图9 中齿轮转动元动作单元的可靠度曲线对比可以发现,两种元动作单元的可靠度变化存在明显差异,因此对实现同一运动功能的不同元动作单元进行可靠性分析才能科学准确地评价产品的可靠性水平.
5 结论
针对机电产品性能可靠性建模和分析困难的问题,本文将系统性能与其功能联系起来,从系统完成其功能的角度出发,将复杂机电产品分解成一系列元动作单元,元动作单元性能可靠性水平对于复杂机电产品性能可靠性的保证具有重要意义,因此对元动作单元的性能可靠性进行了分析研究.
1)采用了功能-运动-动作的FMA 结构化分解方法,分解机电产品可以得到元动作分解树以及一系列元动作单元,并给出元动作单元的结构模型及其必要组成零件类型.
2)分析描述了元动作单元内部每一类型零件的性能退化满足Gamma 随机过程的性质,得到服从Gamma 分布的累积失效分布函数和性能可靠度,同时考虑元动作单元内部结构之间的依赖耦合,结合具有简化依存关系结构良好分析能力的混合Copula函数对元动作单元的性能可靠性进行分析.
3)给出实例,分别采用两种不同元动作单元作为本次实验的分析对象,通过Gamma 过程分析计算得到不同元动作单元的不同假设情况下可靠度曲线与结合混合Copula 函数得到的性能可靠度曲线进行对比,有效地弥补了最弱理论和独立退化假设进行性能可靠性分析的不足,证明了该方法得到性能可靠度曲线的可行性和有效性.
4)实施元动作单元的性能可靠性分析,对于评估和保障机电产品性能可靠性具有重要意义.针对产品完成其功能是由一系列元动作单元共同完成的,因此元动作链的性能可靠性分析问题是下一步有待研究的工作.

