智能网联汽车中心式匝道合流协同控制
江浩斌,胡子牛†,刘擎超,秦洪懋,孟天闯
(1.江苏大学汽车与交通运输工程学院,江苏镇江 212000;2.湖南大学机械与运载工程学院,湖南长沙 410082;3.清华大学车辆与运载学院,北京 100084)
交通拥堵已成为城市发展的痛点问题,匝道合流是造成城市高架道路和高速公路交通拥堵的主要原因之一[1].2014 年,美国城市地区交通拥堵的总成本估计为1 600 亿美元,额外消耗31 亿加仑燃料[2].交通拥堵降低了交通效率,增加了碰撞风险[3],增加了出行时间[4],给乘客带来不适,导致油耗和排放过多[5-6].实际上,匝道合流操作对于驾驶员来说,必须综合考虑周围环境的各类因素.通常,试图合流的车辆可能会在入口匝道上先减速,等待合适的合流机会,同时根据对安全间距和主流车辆速度的判断,以确定加速的程度和时间.即使驾驶员最终顺利完成合流,实际的合流过程也不一定是全局最优的,安全性、经济性和舒适性难以兼顾和保证.
为解决这一问题,自动匝道合流控制能够通过考虑匝道合流过程中复杂的时空约束,协同组织匝道区域内多个车辆的运动,从而保证顺利完成合流,并大大提高合流过程的安全性、效率与燃油经济性.近年来,智能网联汽车技术快速发展,为实现自动匝道合流控制提供了基础.首先,智能网联汽车能够通过车-车通信(V2V,Vehicle-to-Vehicle)实现合流控制操作中的实时通信;其次,智能网联汽车可通过车-路通信(V2I,Vehicle-to-Infrastructure)接收来自合流区域附近的智能基础设施的信息,进一步提高了车辆合流协同控制的可行性[7-10].
智能网联汽车的匝道合流协同控制方法主要可分为中心式方法和分布式方法[11].在中心式方法中,至少有一个任务是由一个中央控制器为所有车辆全局决定的.Jing 等人[12]提出了一个基于多人博弈的合作优化框架和算法,在这个框架中,中央控制器从进入合流区域内的车辆中获取信息,并将每辆车视为一个智能体进行全局优化协调,从而最小化车辆行驶时间、油耗和乘客舒适度的全局收益.Malikopoulos等人[13]使用汉密尔顿分析法提供一个可实时求解的解析闭环解,在保证满足防追尾避撞的硬安全约束下实时求解各车辆的最优加减速.Ntousakis 等人[14]提出了一种纵向轨迹规划方法,将合流问题表述为有限时域最优控制问题,并对其进行解析求解,在实现安全与效率的同时最小化燃油消耗、乘客不适、加速度及其一阶、二阶导数.Rios-Torres 等人[15-16]提出了一种基于燃油经济性的车辆加速曲线在线优化的闭式求解方法,同时避免了在合流区与其他车辆的碰撞.Meng 等人[17]提出了一种基于优化的匝道合流协同控制方法,可以综合提升匝道合流中的燃油经济性和安全性.
在分布式方法中,每辆车根据从道路上其他车辆接收到的信息来确定自己的控制策略.Uno 等人[18]最早在1999 年提出了虚拟车辆合流协同控制的概念,这种方法将匝道上的车辆投影到主干道路上生成虚拟车辆,并通过对同一条道路上的真实车辆与虚拟车辆的纵向控制,优化合流过程.Dan 等人[19]提出了基于虚拟时隙的交通管理概念,所提出的协同合流控制方法能够提升匝道的吞吐量和平均延迟.Pueboobpaphan 等人[20]重点研究了具有不同自动化水平的车辆之间的相互作用,并且保证了人工驾驶车辆能够平滑合流.Cao 等人[21]提出了协同合流的概念,其中主道上的车辆调整速度以适应匝道上试图合流的车辆,利用MPC 方法对两条单行道上的相关车辆优化生成合流路径.Zhang 等人[22]使用一种分布式方法,将硬安全约束下的交叉路口车辆左右转向规划问题构建为优化控制问题进行优化求解.Malikopoulos 等人[23]使用求解完整解析解的分布式方法,解决了无明确交通信号情况下的交叉路口通行优化控制问题,在实现交通吞吐量最大化的同时最小化能源消耗.此外,在与匝道合流协同控制相似的非信控路口协同通行方面,Xu 等通过驶近车辆投影变换设计了基于虚拟队列的协同控制方法,可实现多车在非信控路口的分布式无冲突协同通行[24];Bian 等设计了非信控路口任务分区架构,融合分布式观测、优化与控制方法,实现了多车的无中心协调式协同通行[25].
本文提出了智能网联汽车中心式匝道合流协同控制方法,在合流控制中综合考虑了燃油经济性、安全性等控制目标,可提升匝道合流协同控制的综合性能;其次,本文提出的模型没有对车辆的位置、速度和加速度做出线性或其他形式的运动假设,所计算出的车辆最优运动轨迹更符合实际车辆特性.本文在文献[17]的基础上进一步考虑了随机初始化条件下的匝道控制性能,并评估了协同合流控制对主车道车辆燃油经济性的影响.
本文首先确定并分析所研究场景;然后构建车辆状态方程及合流过程约束条件、初始条件、终止条件以及目标函数,进而建立匝道合流协同控制模型;最后通过数值仿真进行方法验证和分析,并与文献[6]中方法进行对比.
1 研究场景
如图1 所示,考虑一种简化的匝道合流场景,主道与匝道均为单车道.实际上,主道道路一般由多车道组成,本文假设车辆在进入控制区之前已经完成了换道操作,而不需要考虑控制区域的车辆换道行为,因此,主道多车道的问题可以简化为单车道问题.此外,在同一条车道上的车辆遵循先进先出(First In First Out,FIFO)规则,不能进行超车.控制区域定义为图1 中长度为L 的V2I 通讯范围,实际上通常是半径为几百米的范围.匝道合流协同控制系统中仅考虑位于控制区内的车辆.合流点定义为主道中心线与匝道中心线的交点.在本文中仅考虑匝道上有一辆车的情景,标记为车0.主干道上尚未到达合流点的车辆依次标记为车1~车m,如图1 所示.

图1 简化的匝道合流场景Fig.1 Simplified ramp merge scene
匝道合流需要合流车辆(车0)与主道上的车辆协同完成,在主干道上的车辆负责为合流的车辆制造足够安全的间隙,以便合流车辆进行合流汇入.也就是说,它们需要协同调节各自的车速以适应合流车辆.本文假设每个合流区域中都存在智能路侧单元,如图1 所示.控制区内的每辆车都可以与智能路侧单元进行通信,频繁共享其实时信息并接收控制消息.车辆的共享信息包括车辆编号、车辆长度和宽度、位置、速度、加速度、横摆角等.其中一些共享信息是常数,其余信息可以通过车载设备(例如GPS、速度计、加速度计和陀螺仪)实时测量和计算.智能路侧单元收到共享信息后,其内部的数据处理单元将采用本文提出的方法来计算每辆车的最优速度曲线,然后将最优速度曲线发送给各个车辆进行轨迹跟随实现.
如上所述,本文假定所有车辆都是智能网联汽车,即完全配备了定位和V2I 功能设备并能够自主控制自身速度,在控制误差允许范围内跟随最优速度曲线完成合流过程.
2 匝道合流协同控制方法
2.1 匝道合流协同控制模型
本文提出的中心式匝道合流协同控制方法利用匝道合流协同控制模型来计算每辆车的最优速度曲线.匝道合流协同控制模型由状态方程、状态约束、初始和终止条件以及目标函数四个部分组成,进而得到匝道合流控制最优化问题.
2.1.1 状态方程约束
假设每辆车都有相同的动力学特性.对于车辆i,可以容易地推导出以下动力学关系.
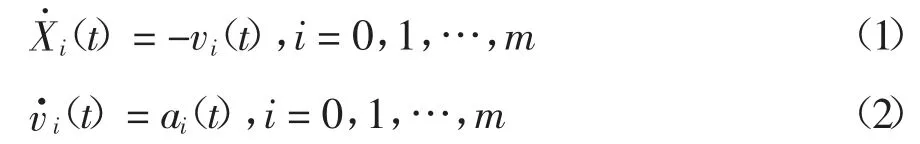
式中:t∈[t0,tend],t0表示初始时间,tend表示合流车辆到达合流点的最终时间,Xi(t)表示在时刻t 车辆i 到合流点的距离,vi(t)和ai(t)分别是车辆i 在时间t 的速度和加速度.另外,定义距离Xi(t)在车辆i 到达合流点之前为正,在车辆i 到达合流点之后为负.
2.1.2 状态约束
首先,所有车辆的速度和加速度应满足边界约束.
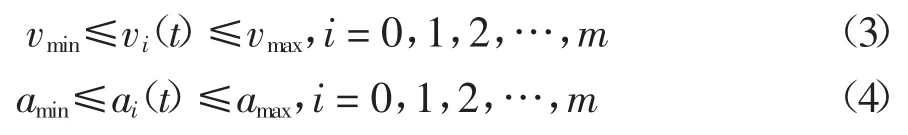
式中:t∈[t0,tend],vmin和vmax分别是车速的最小限制值和最大限制值,amin和amax分别是保障舒适性的加速度最小限制值和最大限制值.
其次,在整个合流过程中,主干道上的所有车辆均应保持与相邻车辆的安全车距.

式中:t∈[t0,tend],δsafe表示最小允许车头间距,即允许的最小安全车距.
此外,当合流车辆到达合流点时,需要确保合流车辆与主道车辆之间具有安全车距,以及所有车辆之间的速度差不能超过安全速度差.
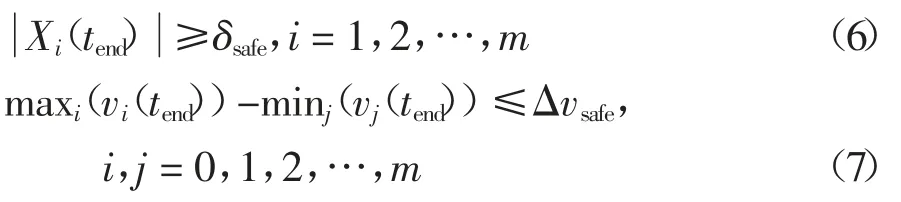
式中:Δvsafe表示安全速度差,可根据实际情况设置合理的值.式(6)中,结合式(10)可知表示在tend时刻主道车辆i 与匝道车辆的距离,因此约束条件(6)保证了在tend时刻合流车辆与主道车辆之间具有安全车距,约束条件(7)保证了在tend时刻所有车辆之间的速度差不能超过安全速度差.
2.1.3 初始和终止条件约束
智能路侧单元可以计算出每辆车距离合流点的初始距离Xi0和初始速度vi0,此外,合流车辆到达合流点的时间是tend,得如下条件.

2.1.4 目标函数
本文综合考虑合流策略在多个方面的性能指标,构建目标函数.
首先,考虑车辆加速度的影响.加速度越高,加速持续时间越长,合流效率越低,燃油经济性和车辆舒适性也越差.因此,目标函数的第一项可以写成:
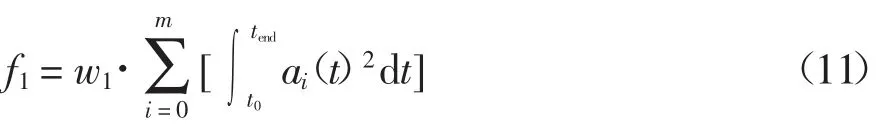
式中:w1表示在整个目标函数中第一项的权重.
其次,在合流过程中希望车速与安全经济速度vd之间的偏差,即(i=1,2,…,m)尽可能小,因为减小这个速度偏差可以使速度调节过程更加稳定,并在合流结束时有利于减小各车速度差.需要说明的是,该项的设计与下一节介绍的优化方法也有关.因此,目标函数中旨在减少合流过程中车辆速度偏差的第二项可以写成:

式中:w2表示第二项在整个目标函数中的权重.
第三,当合流车辆到达合流点的时刻对安全性的要求最高,因此在tend时刻相邻车辆之间的速度差应尽可能小.因此,目标函数中旨在减小tend时刻相邻车辆速度差的第三项可以写成:

式中:w3表示在整个目标函数中第三项的权重,v′表示在合流结束后,主干道上的所有车(包含完成合流的合流车辆)从前到后依次从1 到m+1 获得一个新的编号i′.
于是,总体目标函数为:

2.2 匝道合流协同控制优化问题
结合上述约束条件及目标函数,匝道合流协同控制优化问题为:

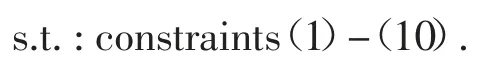
即优化各车辆控制输入以最小化全局目标函数.
在匝道合流协同控制模型中,目标函数中包含积分项:
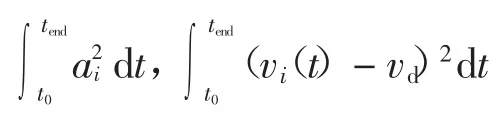
以及在约束条件中含有导数项:
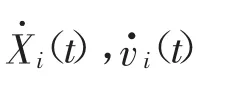
积分项和导数项的存在增加了求解最优化问题的难度,本文采用离散化的思想来简化积分项和导数项的问题.每辆车到合流点的距离Xi(i=0,1,…,m)被离散化为向量Xdci,由一系列瞬时距离组成.
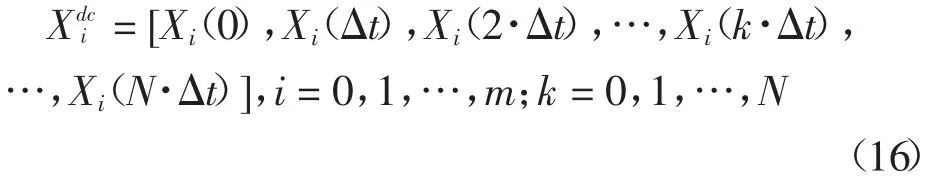
式中:Δt 是时间步长.
定义:

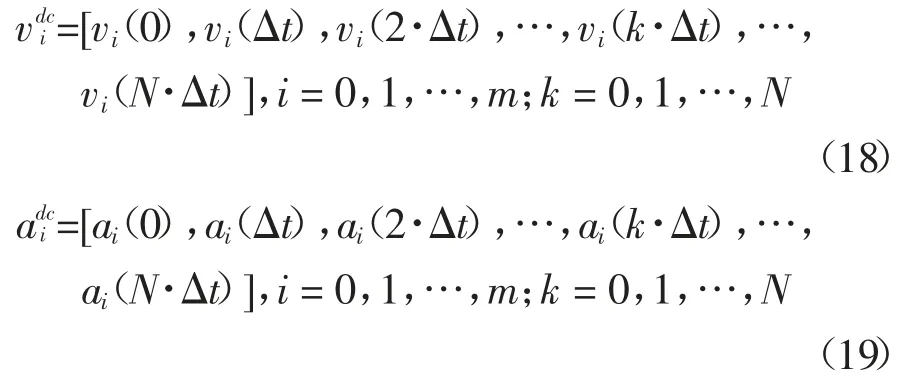
同样地,定义:


离散化后,本文将匝道合流协同控制模型转换为离散的非线性最优化形式.可以通过最优化离散向量中的系列值来获得每个车辆的最优运动.此外,当N 已知时,时间步长Δt 可以确定tend.因此,我们还需要优化时间步长Δt.
实际上,离散化后的模型是一个由线性和非线性约束条件组成的全局非线性规划(GNLP,Global Non-Linear Programming)问题.
GNLP 问题具有如下一般形式:
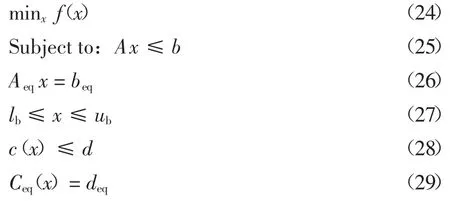
式中:f(x)是包含非线性目标函数的标量函数.满足以下约束条件:
式(25)是线性不等式约束,A 为线性不等式约束系数矩阵,b 为线性不等式约束向量.式(26)是线性等式约束,Aeq为线性等式约束系数矩阵,b 为线性等式约束向量.式(27)是控制变量上下界约束,lb为下界约束向量,ub为上界约束向量.式(27)是非线性不等式约束,c(x)是非线性不等式约束方程向量,d为非线性不等式约束向量.式(29)是非线性等式约束,Ceq(x)是非线性等式约束方程向量,deq为非线性等式约束向量.
针对离散化后的GNLP 问题,后续具体求解过程采用NOMAD 算法[26],NOMAD 算法主要使用MADS 算法(Mesh Adaptive Direct Search,网格自适应直接搜索)来求解非线性最优化问题,适合于上述GNLP 问题的求解.
3 数值仿真
为验证所提出方法效果,首先在100 个随机初始化合流场景进行仿真,以验证方法的有效性;而后在单个特定初始化场景下进行仿真测试,并分析合流车辆的位置对燃油消耗率的影响;最后将该方法与文献[6]中方法进行对比.
3.1 随机初始化仿真验证
3.1.1 仿真设置
为验证所提方法有效性,随机初始化100 个合流场景进行仿真实验.部分模型参数的设置如表1所示.其中,对速度的随机初始化采用期望为安全经济速度vd=20 m/s、方差为1 m2/s2的高斯随机分布,对主道车辆数目、主道和匝道车辆初始距离的随机初始化的统计如表2~4 所示.

表1 匝道合流协同控制模型中的部分参数Tab.1 Some parameters in the cooperative control model of ramp merging

表2 主道车辆数目分布统计Tab.2 Statistics on the number of main road vehicles
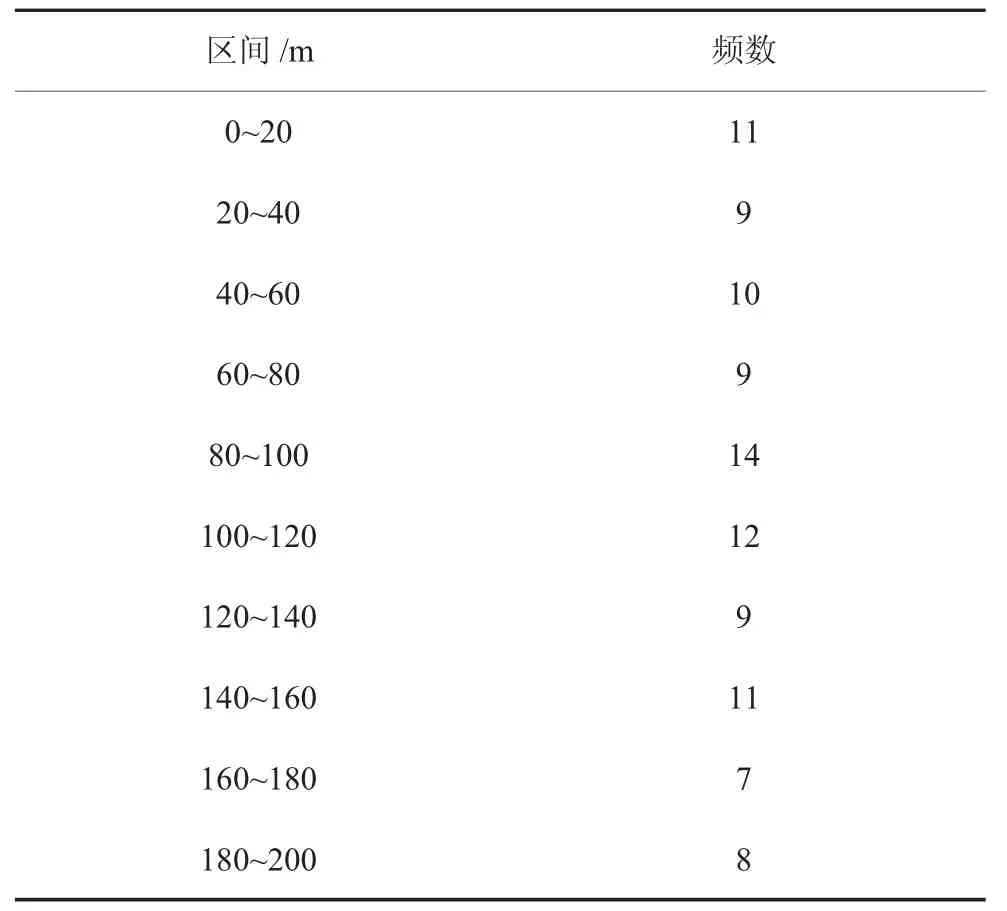
表3 主道第1 辆车初始距离分布统计Tab.3 Statistics of the initial distance distribution of the first vehicle on the main road

表4 匝道车辆初始距离分布统计Tab.4 Statistics of initial distance distribution of vehicles on ramp
3.1.2 结果分析
未能完全成功合流的实验为编号98 和编号100组实验.
编号98 仿真实验的初始条件为:匝道车辆初始速度为70.02 m/s,初始位置为7.15 m;主道上有12辆车,从车辆1 至车辆12 的初始速度依次为(单位:km/h):[72.49,74.53,74.42,71.30,68.81,78.96,69.,2,74.,7,77.30,73.20,71.65,70.29],初始位置依次为(单位:m):[34.48,68.84,96.77,126.57,157.04,187.75,221.08,250.75,285.14,312.64,340.18,369.83].
编号100 仿真实验的初始条件为:匝道车辆初始速度为64.96 m/s,初始位置为60.02 m;主道上有13 辆车,从车辆1 至车辆13 的初始速度依次为(单位:km/h):[67.87,71.08,73.47,73.21,72.96,75.08,64.73,72.85,66.29,69.35,73.81,67.42,68.10],初始位置依次为(单位:m):[8.87,38.53,68.71,100.38,131.23,160.34,189.00,218.80,248.07,284.85,311.37,344.00,371.94].
在100 组合流过程中,编号98 和编号100 仿真所求解出的车辆加速度超出舒适加速度约束条件,其中编号98 实验中的最大加速度达到了117.74 m/s2,编号100 实验中的最大加速度为11.66 m/s2.仿真计算求解器返回的结果表示,两组实验得到的计算结果并不是收敛解,即在仿真环境计算能力有限的条件下,求解时间过长,求解器未能求出收敛解即退出求解运算.
在合流完成时刻,所有相邻车辆之间均满足安全车距条件的实验组数为100.匝道车辆与前后车自然也满足安全车距条件;在合流完成时刻,匝道车辆与前后车速度差处于±5 km/h 范围内,则认为合流完成后的车辆速度具备较好的安全性,在100 组实验中,匝道车辆与前车速度差处于±5 km/h 范围内的实验组数为100,匝道车辆与后车速度差处于±5 km/h范围内的实验组数为99,编号100 的速度差为9.49 m/s,超过5 km/h.
综上所述,在100 组随机初始化实验中,有98组实验能够顺利求解,说明本文提出的方法针对不同的初始化合流场景都具有较好的效果.
3.2 单场景仿真验证
3.2.1 仿真参数设置
本节生成一个随机合流场景Ⅰ,进一步验证本文所提方法的效果.随机生成结果如下.
在场景Ⅰ中,初始时刻主干道有8 辆车,从车辆1 到车辆8 的初始速度依次为(单位:km/h):
[76.99,69.57,77.46,73.31,71.89,73.29,71.63,71.78]到合流点的初始距离依次为(单位:m):[162.94,196.61,222.09,253.82,284.46,311.84,340.97,371.66]
对于合流车辆,初始速度v00为73.50 km/h,初始距离x00为254.09 m.参数设置如表1 所示.
仿真使用文献[27]中提出的模型计算每辆车的燃油消耗率,具体为:
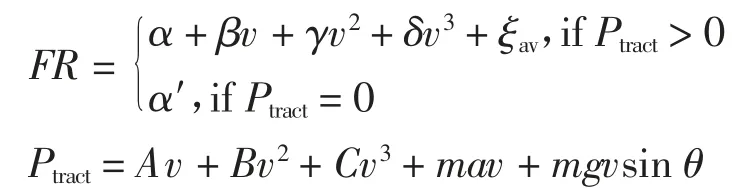
其中FR 是燃油消耗率,Ptract是牵引功率,v 是速度,α是加速度,其中参数可以根据文献[27]进行选择.
3.2.2 结果分析
根据场景Ⅰ及其参数设置,通过仿真计算,得到距离、速度、加速度的优化结果如图2~4 所示,合流过程中主道上不同位置车辆的燃油消耗量和燃油消耗率分别如图5 和图6 所示,燃油消耗具体数值如表5 所示.

图2 优化的位置曲线Fig.2 Optimized position curves

图3 优化的速度曲线Fig.3 Optimized speed curves
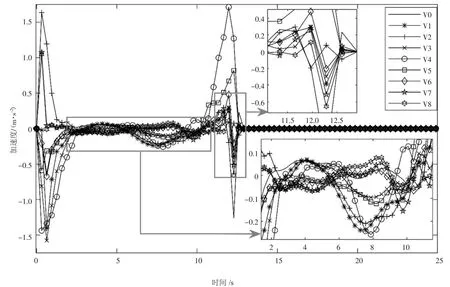
图4 优化的加速度曲线Fig.4 Optimized acceleration curves
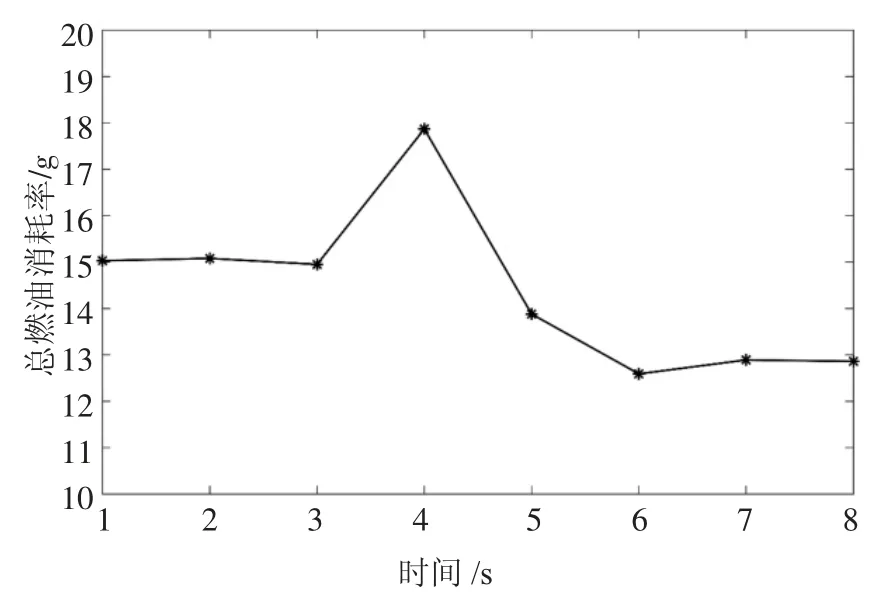
图5 主道车辆总燃油消耗量Fig.5 Total fuel consumption of main road vehicles
此外,优化得到的Δt 为0.31 s.由于N 取40,所以最终时间tend为12.44 s.
图2 表示的是经过最优化得到的车辆到合流点的距离变化.从图中可以看到,合流车辆在主干道路上的车辆3(V3)和车辆4(V4)之间合流汇入.在初始时刻,合流车辆到合流点的距离约等于车辆4 到合流点的距离.在合流过程中,车辆3 和车辆4 之间的距离逐渐变大,以便为合流车辆创建足够的汇入间隙.当合流车辆在tend时刻到达合流点时,所有9辆车之间的车头间距依次为(单位:m):[34.31,27.60,30.93,20.05,20.50,21.40,25.40,29.85]
很明显,所有9 辆汽车都满足约束(5)-(7).

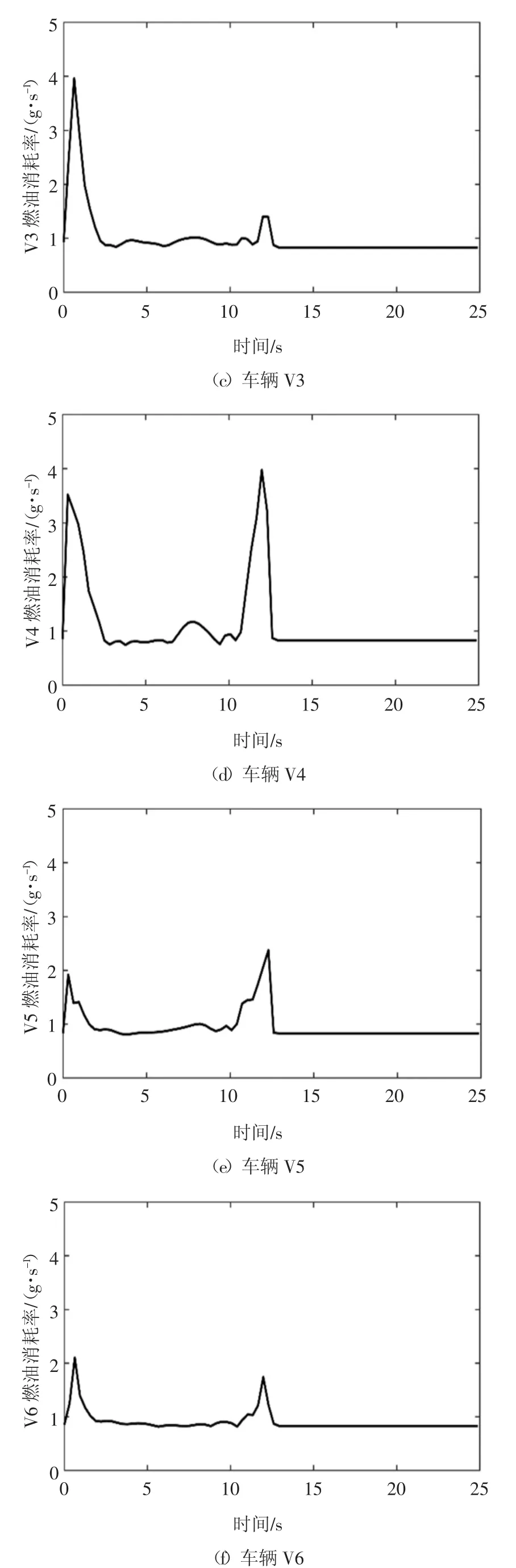
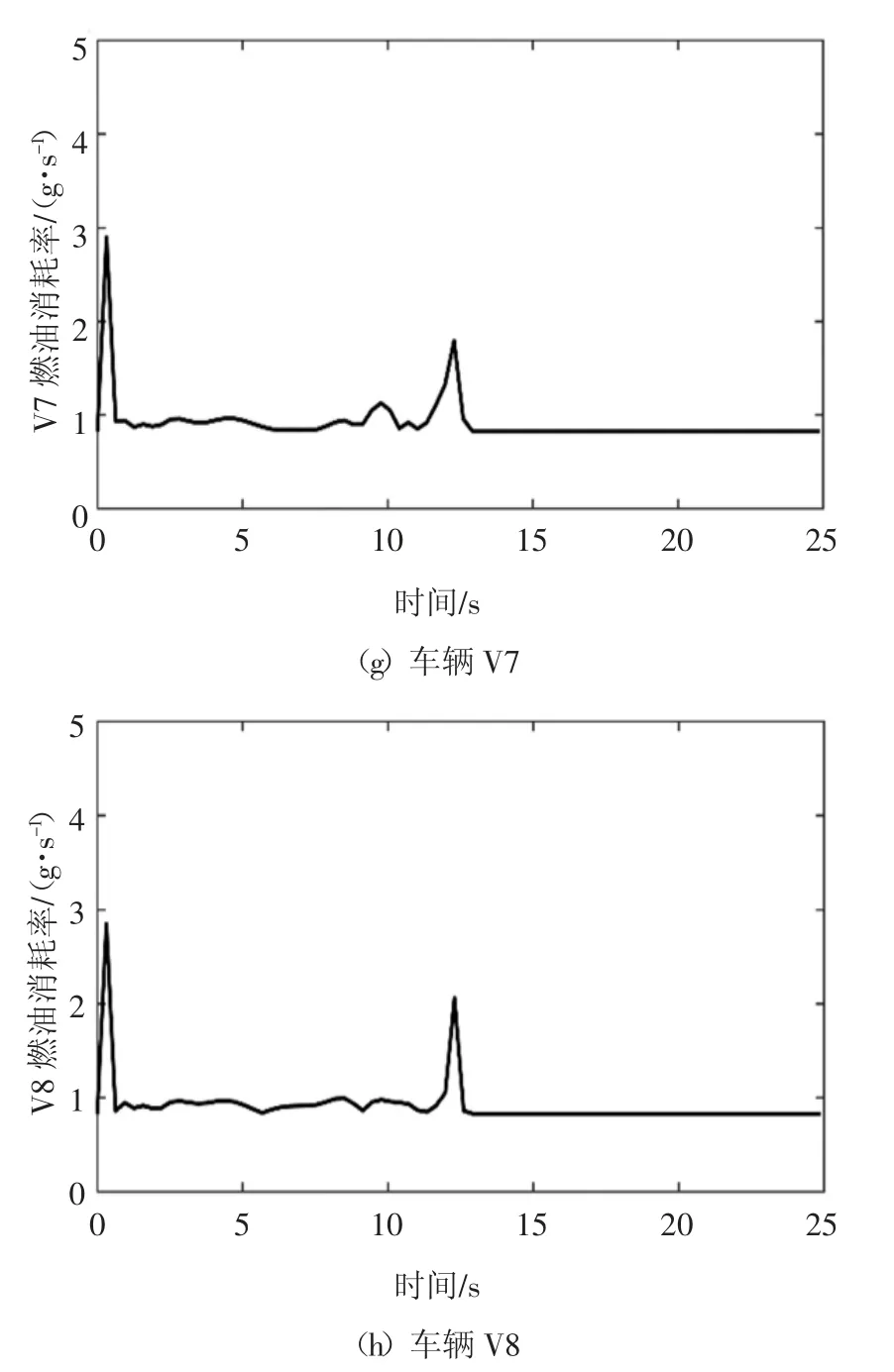
图6 V1~V8 燃油消耗率曲线Fig.6 V1~V8 fuel consumption rate curves
如图3 所示,在合流过程的早期和后期,主干道路上车辆的速度曲线变化很大且变化很快,但在中间阶段则长时间保持稳定,近似为匀速行驶.这种速度调节模式正是目标函数所包含的三项所期望的,即尽量减小车辆加速度及其持续时间,尽量减小速度偏差(i=1,2,…,m)和在tend时刻相邻车辆之间的速度差.
如图4 所示,车辆加速度曲线的模型符合上面讨论的内容.

表5 合流过程中的总燃油消耗量Tab.5 Total fuel consumption during merging
在图5 中,主道8 辆车中高于平均燃油消耗量的是V1~V4,说明对合流插入位置附近以及较前的车辆燃油消耗量影响较大,且离插入位置越近受影响越大,这是因为合流插入位置附近以及较前的车辆需要通过加速或者减速为合流车辆制造安全车间距.油耗最大值出现在V4,由图6 可以看出,在合流完成时刻前后,V4 的燃油消耗率明显增大,且增大幅度明显大于该时间段其它车辆的燃油消耗率.在图6 中,燃油消耗率在合流过程的初期和末期都很高,这是由于在初期和末期车辆的加速度大造成的,而在中期行驶时,车辆以几乎恒定的速度行驶,燃油消耗率在很长一段时间很低.
通过上述仿真,进一步验证了本文所提方法具有预期效果,并分析了合流车辆的位置对燃油消耗率的影响以及产生原因.
3.3 与其它方法对比仿真验证
3.3.1 对比设置
文献[6]将匝道合流协同控制问题表述为无约束的最优化问题,并应用汉密尔顿分析得出了闭环解析解.每辆车i 的最佳速度分别为:
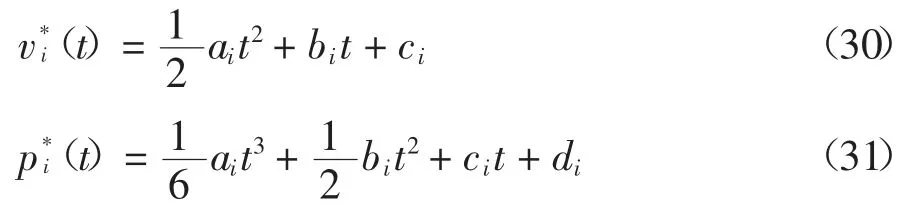
式中:ai,bi,ci,di为常数,可以通过以下方式计算:

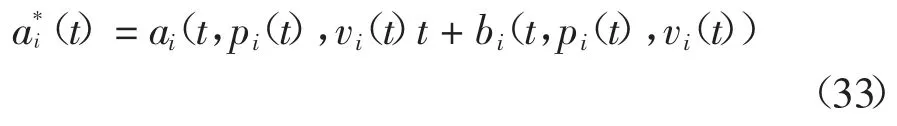
为将本文所提出的方法与[6]中的提出的方法进行对比,设置合流场景Ⅱ,其中初始时刻有3 辆车在主道上,其到合流点的初始距离依次是[200,225,250](单位:m).合流车辆的初始距离为230 m.所有车辆的初始速度为72 km/h.仿真参数设置如表1 所示.
3.3.2 仿真结果对比分析
基于场景Ⅱ进行仿真计算后,基于文献[6]中的方法和本文提出的方法得到的最优结果分别如图7和图8 所示.两种方法都是利用[27]中提出的燃料消耗模型,并且所有参数相同.
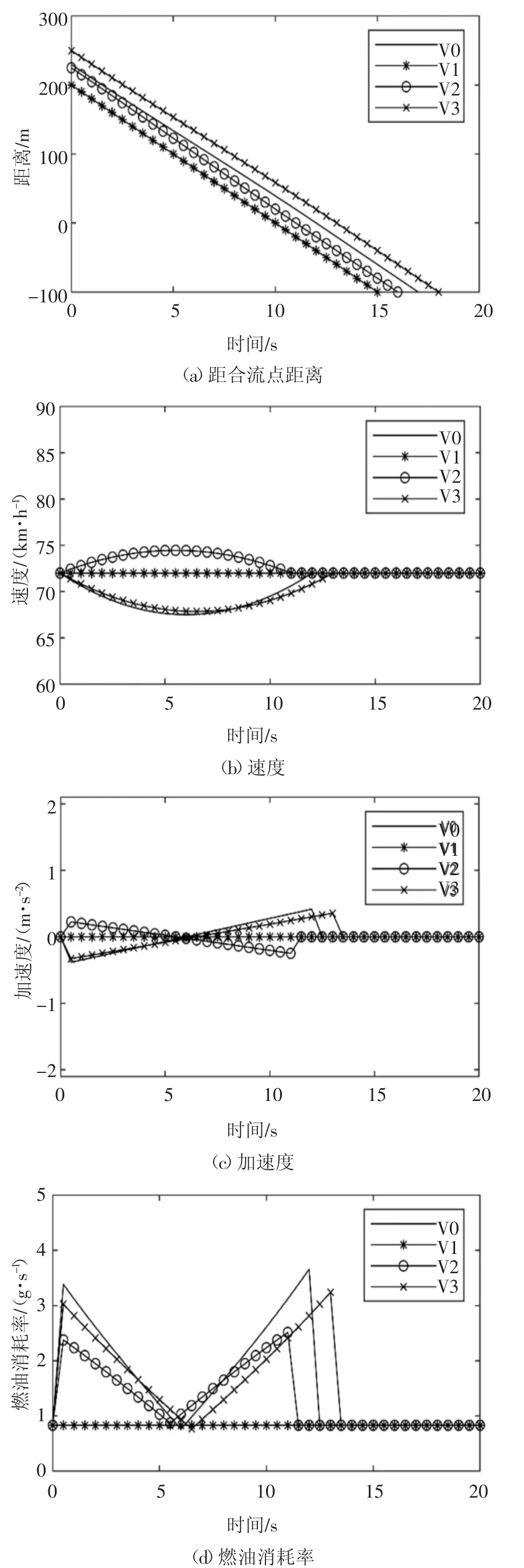
图7 文献[6]中基于场景Ⅱ的方法的结果Fig.7 Results of the method based on scenario Ⅱ in literature[6]

图8 本文基于场景Ⅱ的方法的结果Fig.8 The results of the method based on scenario Ⅱ in this article
首先,本文从合流效率的角度比较了这两种方法.合流时间tend可以反映合流车辆的合流效率.文献[6]中的方法获得tend=12.00 s,而本文的模型获得tend=11.92 s.主干道上的最后一辆车辆到达合流点的时间可以反映主干道上的车辆合流效率,文献[6]的方法所得结果为13.00 s,而本文方法所得结果为12.90 s.此外,这两种方法的车辆等待时间(车辆停止和等待的总时间)都为0 s.因此,在合流效率方面,本文所提出的方法相比文献[6]中的方法略微有提升,但差别不是很大.
然后,从燃油经济性的角度比较这两种方法.在图7(d)中,两种方法的最大燃油消耗率均约为4 g/s.但是与文献[6]中的方法不同,本文提出的模型中的燃油消耗率仅在早期和后期才变高,而在大多数合流过程中却保持在较低水平.关于高油耗率的平均持续时间(燃油消耗率在2 g/s 以上),如表6 所示,文献[6]中方法是4.80 s,本文提出的方法是0.77 s,降低了83.96%.如图9 所示,使用本文所提出的方法可以大大减少燃油消耗.经计算,可得到每辆车在整个合流过程中的平均油耗,用文献[6]中的方法是20.01 g,用本文所提出的方法是11.53 g,降低了42.38%.因此,本文提出的模型显著提高了合流过程中的燃油经济性.
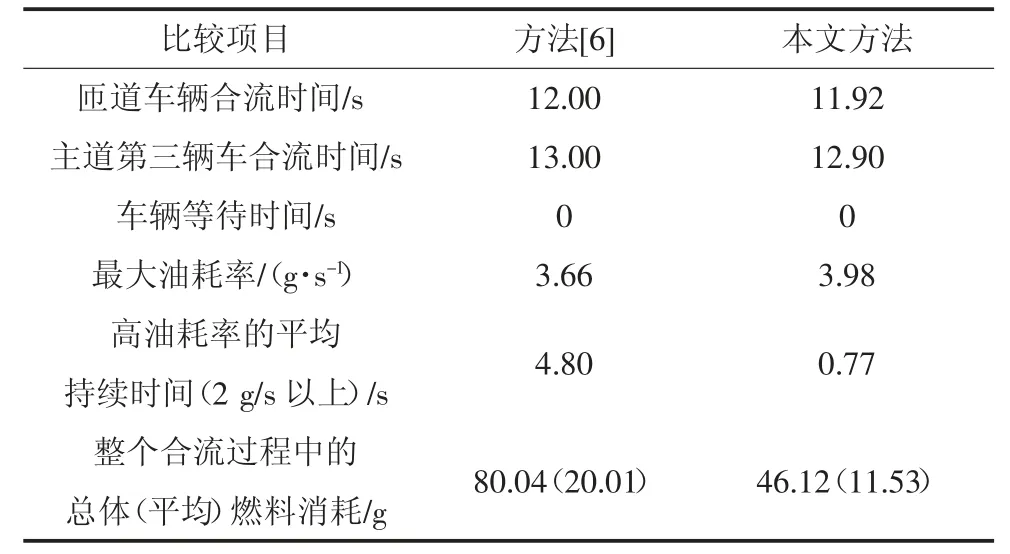
表6 两种方法的性能比较Tab.6 Performance comparison of the two methods

图9 两种方法在累计油耗方面的比较Fig.9 Comparison of the two methods in terms of cumulative fuel consumption
4 结论
本文提出了基于智能网联汽车的中心式匝道合流协同控制方法,建立了匝道合流协同控制模型,通过数值仿真验证了所提出方法的有效性.仿真结果表明,本文所提出方法与文献[6]中方法具有基本相同的合流效率,但可有效提升协同合流控制中的车辆燃油经济性.
本文所研究的合流问题中,车辆与路侧智能设施之间仅在初始时刻进行短暂通信,在后续研究中可增加对规划后车辆动力学控制的研究,增加合流过程中的通信影响,对通信时延、丢包作为重要因素进行建模分析.不同的匝道结构参数对车辆动力学控制的影响较大,尤其是横向动力学控制,因此在后续研究中可考虑不同匝道结构参数的影响.此外,今后的研究也将集中在更复杂场景下的合流控制问题上,比如匝道上车辆数目增多、主干道上车道数量增加并允许换道等.

