“一带一路”沿线主要国家股指市场风险传染效应*
乔新尧,卢俊香,2*
(1.西安工程大学 理学院,陕西 西安 710048; 2.西安理工大学 经济与管理学院,陕西 西安 710048)
2013年9月,习近平总书记在中亚和东南亚国家交流访问期间,提出了“一带一路”的倡议。随着“一带一路”的提出,中国与其他“一带一路”沿线国家之间金融市场的联系日益紧密。研究“一带一路”对股票市场波动的影响,以及中国和沿线主要国家股票市场间的相关结构,有利于为中国进一步推进“一带一路”建设、加强与沿线各国的贸易合作以及共同维护金融市场的稳定;可以为各个国家金融市场的监管部门提供一些参考,更利于给投资者进行投资组合时提出合理建议以减小投资风险。
金融时间序列大多呈现出尖峰厚尾、波动聚集性的特点。1959年,SKLAR首次提出了Copula函数的概念,将多维随机变量的联合分布函数与各边际分布函数连接起来[1],为学者们研究变量之间的相关关系提供了一个新的方法。EMBRECHTS et al首次将Copula函数应用到金融管理领域,提供了新的研究金融市场相关结构的方法[2]。MOKNI et al将GARCH模型和Copula函数结合起来共同研究股票市场的相关性[3-4]。国内,张尧庭首次详细介绍了Copula函数的理论并将其运用于金融风险分析中[5]。刘红玉运用Copula函数研究了上证综指与深证成指的相关结构[6]。曹境鸽运用GARCH(1,1)-GED-Copula模型度量ETF基金投资组合的风险,发现相关性较强的投资组合的风险要高于相关系数小的组合风险[7]。
但是之前大多是借助单一的Copula函数研究两两资产间的相关结构,如果要研究2只以上股票之间的相关性及度量投资组合风险价值,单一的Copula函数明显存在着局限性。HU最早提出了混合Copula函数模型(M-Copula) 来度量变量之间的相关关系[8]。ZILKO et al通过多元混合 Copula 函数对金融市场进行研究[9]。国内,陈秋林等建立M-Copula模型并计算VaR值[10-12]。徐麒等利用M-Copula函数研究消费者价格指数(CPI)和生产者价格指数(PPI)两者间的相关性,结果表明CPI和PPI在经济衰退时期的相关性更强[13]。刘祥东等运用M-Copula函数度量我国4个行业指数投资组合的风险价值,发现4个行业指数具有下尾相关性,更可能在同一时间发生下跌的情形[14-15]。在刻画高维金融市场的相关结构时,选取M-Copula函数模型比单一的Copula函数更灵活,为研究多个变量之间的相关关系拓宽了思路。
同时,风险度量对投资者来说至关重要。最初,MARKOWITZ提出了均值方差模型来描述风险[16],但是金融时间序列往往不服从正态分布,因此也有局限性。 随后,摩根公司提出了VaR指标,成为银行、证券公司等进行度量投资风险的重要工具。郑文通最早将VaR方法引入中国,全面地介绍了VaR方法[17]。李丽梅等研究了由股票指数和股指期货组合的VaR,发现SVt-EVT-Vine Copula 模型度量的投资组合风险更准确合理[18]。DU et al用Copula函数来分别研究汇率以及银行的相关关系,并计算其风险价值[19-20]。在度量风险方面,VaR方法明显比均值方差模型效果好。
在“一带一路”背景下,对于沿线主要国家金融市场相关结构的研究日益被重视。王满仓等根据协同理论分析了离岸金融与“一带一路”之间的关系[21];黄雯晶利用溢出指数模型研究中国与其他沿线国家股市间的波动溢出效应[22]。这些研究基本是从政治经济学的角度来分析“一带一路”背景下金融市场的相关结构,没有运用简单的数学模型以及大量数据实证。另外,国内外对于金融市场的相关结构的研究集中于金砖国家、发达国家,很少有涉及“一带一路”沿线国家。因此,在已有的多维金融市场的相关性研究基础上,本文以VaR作为风险度量指标,先使用GJR-GARCH(1,1)-t模型来刻画各股指市场收益率的边缘分布;再运用M-Copula函数来连接各边缘分布刻画股指市场间的相关结构;最后计算不同权重、不同置信水平下的资产组合的风险价值。
1 相关理论
1.1 边缘分布
在构建多维金融市场的相关结构之前,需要先确定单变量的边缘分布。研究表明,金融收益率序列往往呈现出“尖峰厚尾”“有偏”,并且还会出现波动聚集性的特征。 GLOSTEN et al提出了GJR-GARCH模型[23],该模型能更准确地捕捉金融序列的波动聚集性和“杠杆效应”。考虑到收益率序列的厚尾性,本文拟用刻画金融序列厚尾性的t分布结合GJR-GARCH模型拟合股指收益率残差。GJR-GARCH(1,1)-t模型如下:

1.2 M-Copula函数模型
Copula函数的概念由1959年SKLAR回答多维联合分布函数和边缘分布之间的关系时提出,即联合分布函数可以由Copula函数和边缘分布函数共同表示,数学表达式如下:
F(x1,x2,…,xn)=
C(F1(x1),F2(x2),…,Fn(xn)),
(4)
其中,x1,x2,…,xn为n个随机变量,F(x1,x2,…,xn)为变量x1,x2,…,xn的联合分布函数,F1(x1),F2(x2),…,Fn(xn)分别为变量x1,x2,…,xn的边缘分布函数,C(F1(x1),F2(x2),…,Fn(xn))为n元Copula函数,当F1(x1),F2(x2),…,Fn(xn)连续时,Copula函数唯一。
如果对(4)式求导,得到:
f(x1,x2,…,xn)=
(5)
其中,f(x1,x2,…,xn)表示变量x1,x2,…,xn的联合密度函数,fi(xi)为变量xi(i=1,2,…,n)的密度函数,且
c(F1(x1),F2(x2),…,Fn(xn))=
令ui=Fi(xi),i=1,2,…,n,则
(5)式表明多元联合密度函数f(x1,x2,…,xn)可由多元Copula函数c(F1(x1),F2(x2),…,Fn(xn))与各边缘密度函数fi(xi)(i=1,2,…,n)乘积共同表示。
金融领域最常用的Copula函数多属于椭圆类Copula函数族和阿基米德Copula函数族。不同类型的Copula函数对于变量之间的相关性的捕捉程度有所不同。其中,椭圆类Copula函数(正态-Copula和t-Copula函数)刻画对称的尾部相关结构;阿基米德族Copula函数(Gumbel-Copula, Clayton-Copula和Frank-Copula函数)分别描述非对称的上尾相关结构、非对称的下尾相关结构以及对称的相关结构。由于不同的Copula函数刻画不同的尾部相关结构,因此将几种Copula函数组合起来,即混合Copula函数模型(M-Copula)共同研究相关结构,拟合的比只使用单一Copula函数的好。本文将Gumbel-Copula,Clayton-Copula和Frank-Copula函数线性组合起来共同研究5只股指间的相关结构。五元M-Copula函数的模型如下:
CM(u1,u2,u3,u4,u5)=ω1Cg(u1,u2,u3,u4,u5;θ1)+
ω2Cc(u1,u2,u3,u4,u5;θ2)+ω3Cf(u1,u2,u3,u4,u5;θ3)。
其中,CM(u1,u2,u3,u4,u5)为M-Copula函数,Cg(u1,u2,u3,u4,u5;θ1)表示Gumbel-Copula函数,Cc(u1,u2,u3,u4,u5;θ2)表示Clayton-Copula函数,Cf(u1,u2,u3,u4,u5;θ3)表示Frank-Copula函数;ω1,ω2和ω3(ω1,ω2,ω3≥0)为权重,且满足ω1+ω2+ω3=1。
1.3 M-Copula模型的参数估计
一般采用极大似然估计法(Maximum Likelihood Estimate,MLE)来估计Copula函数的参数,但是M-Copula模型中不仅包含各Copula函数的参数,而且包括各权重参数。因此在估计该模型中的参数时,仅仅使用MLE方法是远远不够的,需要在MLE方法的基础上结合EM算法和BFGS算法。具体方法如下:
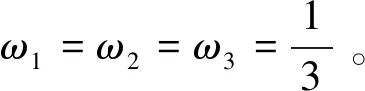
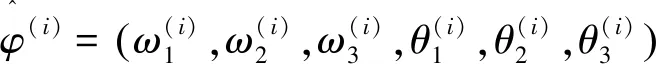
Step3: EM算法的E步,即求出增加了缺失数据后的完整数据Y后的对数似然函数关于缺失数据的条件期望:

Step4: EM算法的M步,即对上式求最大值。在此步中,采用BFGS算法来进行。
1.4 M-Copula-GJR-GARCH(1,1)-t模型下的投资组合的风险价值
在险价值(Value at Risk, VaR)方法是度量金融市场投资组合的风险的主流方法。VaR指在给定置信水平的条件下,由于金融市场波动而导致的资产组合在未来一段时间内可能出现的最大价值损失,即P(Y≥VaR)=α,其中,Y表示金融资产(或组合)在未来某时间内所承受的损失值。Y=-R,R表示金融资产的收益,α为置信水平。
本文使用Monte Carlo模拟方法计算基于M-Copula模型的投资组合的VaR。模拟过程为:
(1) 根据已得到的M-Copula模型,模拟出N组服从均匀分布的Copula随机向量(u1,t,u2,t,u3,t,u4,t,u5,t),t=1,2,…,T,T为Monte Carlo模拟的次数。
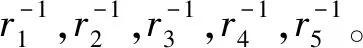
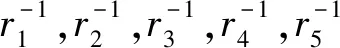
(4) 通过GJR-CARCH(1,1)模型的波动率方程,得出T+1天每只股票可能的日收益率Ri(i=1,2,…,5)。
(6) 根据P(Y≥VaR)=α计算资产组合的风险价值。
2 实证分析
本文在“一带一路”背景下,选取2013年10月8日至2019年11月15日“一带一路”沿线5个国家的股指数据的日收盘价,分别为沪深300指数、俄罗斯RTS指数、富时新加坡STI指数、孟买SENSEX30指数、日经225指数(数据来源为Wind数据库),得到实际有效数据共1 492组(删除了股票收盘价缺失值,使得5只股指数据的收盘日期相同)。对日收盘价一阶差分并扩大100倍:
rt=100×[ln(Pt)-ln(Pt-1)],
其中,rt为对数收益率,Pt为股票日收盘价。收益率序列的边缘分布建模,M-Copula函数的参数估计以及投资组合的在险价值计算均在Matlab 2016a软件中进行。
2.1 描述性统计
先对5只股票的对数收益率进行描述性统计,其结果如表1所示。孟买SENSEX30指数的平均收益率最大,而俄罗斯RTS指数的平均收益率最小,为负值。从标准差来看,俄罗斯RTS指数的波动最大,而富时新加坡STI指数的波动最小。另外,5只股票的偏度均小于0,峰度均大于3,这表明了金融收益率的“尖峰厚尾”性。表1数据显示5只股票收益率的J-B检验的统计量的P值均≤0.05,所以均拒绝原假设, 即不服从正态分布。由于收益率不服从正态分布,因此不能运用均值方差模型来度量投资组合的风险。

表1 股指收益率的描述性统计Tab. 1 Descriptive statistics of stock index returns
2.2 边缘分布建模
在进行边缘分布构建之前需要先检验各只股票指数的对数收益序列是否满足GARCH建模要求。因此,首先对其进行单位根检验,再对其作异方差性检验。检验结果如表2所示,由ADF检验和PP检验的P值均≤0.05有各股指收益率数据不存在单位根,即为平稳的时间序列。进一步根据拉格朗日乘子检验(LM检验)方法进行异方差性检验,由ARCH-LM的P值均≤0.05有各收益率序列均具有ARCH效应,因此,适合用GARCH模型拟合。

表2 股指收益率的单位根检验及异方差检验Tab. 2 Unit root test and heteroscedasticity test of stock index return rate
下面,将采用GJR-GARCH(1,1)-t模型对各对数收益率序列进行边际建模,表3为各参数的估计结果。从表3数据可以看出,各收益率序列具有持续性波动的特点。另外,从参数γ观察到除沪深300指数,其余四支股指均存在杠杆效应。由参数ν可知,俄罗斯RTS指数收益率序列自由度最大,出现极端事件的概率最小;相反,日经225指数收益率序列自由度最小,出现极端事件的概率最大。k-s检验显示P值均>0.01,表明标准残差经概率积分变换后为[0,1]上的均匀分布。
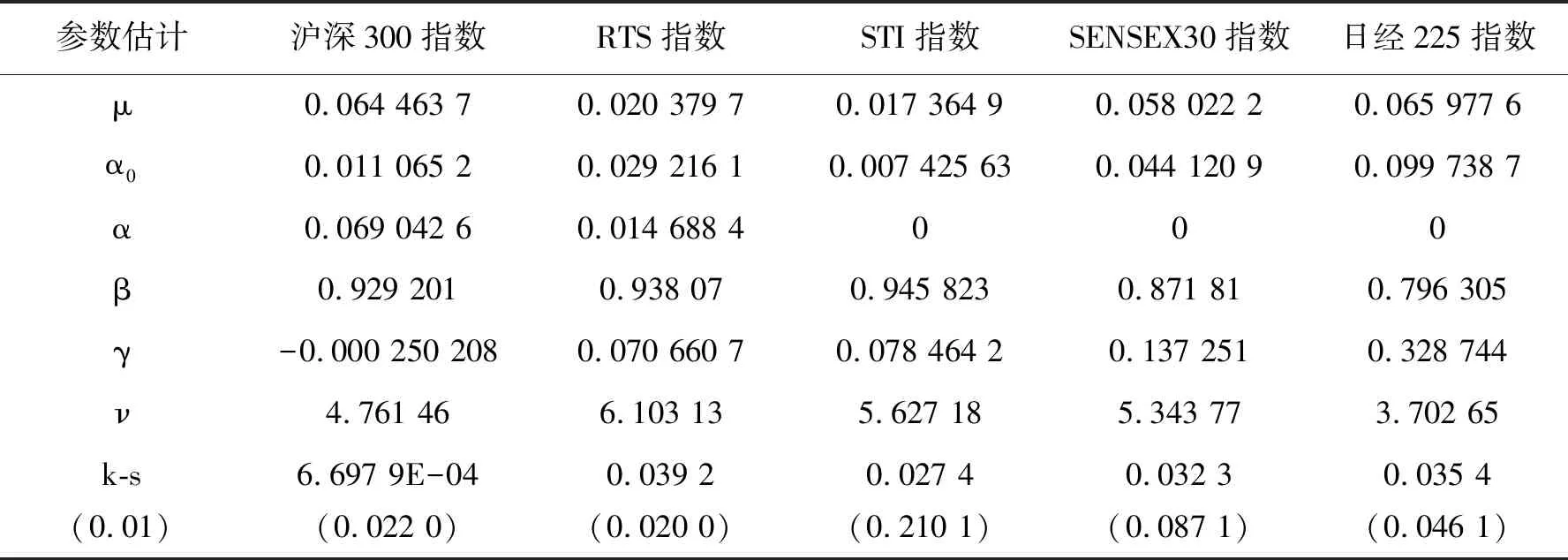
表3 GJR-GARCH(1,1)-t模型的参数估计Tab. 3 Parameter estimation of GJR-GARCH (1,1) -t model
2.3 M-Copula参数估计
对股指收益率的边缘分布建模后,再对进行了概率积分变化后服从[0,1]均匀分布的残差序列进行M-Copula模型拟合,进而研究5只股指之间的相关关系。将极大似然估计法与EM算法、BFGS算法结合起来对M-Copula函数模型进行参数估计,得到最终的权重参数ω1,ω2,ω3和各Copula相依参数θ1,θ2,θ3,其结果如表4所示。Clayton-Copula函数所占的权重最大为0.541 8,表明5只股票具有较强的下尾相关性,更可能发生同时下跌的情况;Gumbel-Copula函数所占的权重次之为0.347 6,说明5只股票之间的上尾相关性较下尾相关性弱;Frank-Copula函数的权重最小为0.110 6,表明5只股票之间的对称相关性最弱。

表4 M-Copula函数模型的参数估计Tab. 4 Parameter estimation of M-Copula function model
2.4 VaR的计算
利用Monte Carlo模拟,随机生成T=5 000组服从上述五维M-Copula函数的随机向量(u1,t,u2,t,u3,t,u4,t,u5,t),t=1,2,…,T,并通过GJR-GARCH(1,1)-t模型所拟合的各收益率序列得到5只股票的模拟收益率,随后分别计算如表5所示的3组不同权重下的投资组合的收益,最后计算在置信水平为95%和99%条件下各资产组合的风险价值VaR。

表5 投资组合的权重Tab. 5 Portfolio weight
表6显示不同置信水平下的单一资产和资产组合的VaR,从表6中数据可以看出,就单一资产而言,日经225指数的VaR值最大,表现出日本股票市场的风险较高;RTS指数VaR值最小,表现出俄罗斯的股票市场风险较小。其次,单一资产和资产组合的VaR值均随着置信水平的增大而增大;而在同一置信水平下,单一资产的风险要大于资产组合的风险。说明投资者可以通过有选择性地组合资产来分散非系统性风险。3种不同投资权重的资产风险也不同,因此,权重系数的选择对资产组合的风险有一定的影响。提醒投资者在金融投资的时候应避免只大量投资某一个股票,适当的投资组合能减小投资风险,并且在组合投资时把握好不同的投资权重以获得更大的收益。

表6 不同置信水平下的VaR值Tab. 6 Value at risk under different confidence levels
3 总结
“一带一路”的提出对亚洲国家的经济发展起到了重要的促进作用。“一带一路”沿线国家之间金融合作逐渐深入,因此对“一带一路”沿线国家股票市场间相关结构的研究以及度量金融风险就很有必要,这既能为金融市场的共同发展提供参考,又能为投资者提供建议。本文首先使用GJR-GARCH(1,1)-t模型拟合各股指的收益率; 其次选择M-Copula函数模型对5只股票之间的相关结构进行描述,分析了“一带一路”沿线5个国家股票市场的相关性;最后,运用Monte Carlo模拟方法度量投资组合的风险价值。主要结论如下:
(1) 使用GJR-GARCH(1,1)-t模型来拟合单只股票收益率序列时,除沪深300指数,其余4支股指均存在杠杆效应。更加说明中国、俄罗斯、新加坡的投资者更倾向于视股票投资为高风险高回报的投资,在股票价格增长时,会更大可能性地抛售股票以此获利;在股票价格持续走低时更倾向于继续持有股票, 等待价格反弹。印度和日本的投资者更倾向于在股票价格持续增长时保留股票,从而使得股票波动率下降,市场平稳。
(2) 利用M-Copula函数模型研究5只股票的相关结构时,不难发现5只股票具有较强的下尾相关性,且上尾相关性较下尾相关性弱,更可能发生同时下跌的情况。表明5只股票之间的对称相关性最弱。每个国家的经济发展程度不同,资产组合间的相关关系在金融市场总环境的影响下,表现出来的反应程度也不一样。 通过推动“一带一路”在全球范围的实施,可以稳定金融市场结构,带动我国以及沿线国家的经济发展。但是,在经济全球化和“一带一路”发展模式的影响下,一个国家的股票市场价格波动也会影响其他国家的股票价格波动,金融市场的监管部门应时刻关注全球股票市场的波动情况,严控风险,使得金融市场稳健运行。
(3) 在度量资产组合的风险价值时,单一资产和资产组合的在险价值VaR均随着置信水平的增大而增大;而在同一置信水平下,单一资产的风险要大于资产组合的风险。并且,在不同的投资权重下,资产组合的风险也存在着明显的差别。因此,投资者在金融投资时如果只考虑投资其中一种股票时,应选择风险价值相对较小的,或者选择适当的投资组合,以此减小投资风险。
本文的研究仍然存在着一些不足之处。刻画股票市场之间的相关结构也可能会随着时间的变化而变化,即Copula函数的参数是静态不变的,这可能对刻画相关结构时造成一定的误差。此外,在险价值VaR有一定的局限性,不是一致性风险度量指标,即不满足次可加性。因此,下一步的研究可以考虑结合动态Copula模型来更准确地度量资产价格的风险价值。

