一种新的基于离散对数的盲签名方案及其应用*
刘晓红
(运城学院 数学与信息技术学院,山西 运城 044000)
1982年CHAUM首次提出了基于RSA的盲签名概念[1],可以用来保护签名者的隐私,是一种特殊的数字签名方案。在此之后各种基于因子分解问题、离散对数问题、二次剩余问题、双线性对问题以及各种具有特殊性质的指定验证者的盲签名方案、具有消息恢复功能的盲签名方案、代理盲签名方案等相继被提出[2-4]。盲签名就是指签名人在真实消息被盲化后对其进行的签名,并且消息脱盲公布后不能追踪到此消息。盲签名方案除了具备普通数字签名方案的性质之外,还有其特有的性质,如盲性与不可链接性。由于这两大特性,使得盲签名方案被广泛应用于各种电子货币,电子投票,电子拍卖及电子现金系统中。
1994年CAMENISH et al首次提出了基于离散对数的盲签名方案[5]。1995年HARN对其进行了安全性分析[6],发现其不满足盲签名方案的不可链接性。针对文献[6]提出的攻击,2005年LEE et al提出了一种改进的方案[7],接着WU et al提出了该方案的简化版[8],马冬兰等对其进行了安全性分析,并给出了一个攻击以及改进的方案[9]。2017年毛昱昉等提出了一种基于身份的盲签名方案[10],但是该方案也用到了双线性对的运算。2018年廖小平提出了一种基于证书的盲签名方案[11],该方案虽然解决了传统密码系统的秘钥和证书的管理问题,但是缺乏必要的安全性证明。2019年左黎明等提出了一种可证安全的短的盲签名方案[12],但是因方案中存在双线性对的运算从而使得开销较大。2019年王方鑫提出了一种基于RSA的盲签名方案[13],虽然其没有双线性对的运算,但是方案缺少盲签名方案中必要的安全性证明。本文在此基础上,提出了一种更加简单的无双线性对的盲签名方案,并对其进行盲性、不可链接性、不可伪造性以及效率分析。最后结合文献[14]的代理签名技术,在提出的盲签名方案的基础上给出了一种代理盲签名方案,并证明其满足代理盲签名方案的可区分性及不可伪造性。
1 预备知识
本文提出的方案基于离散对数问题(Discrete Logarithm Problem, DLP)以及Hash函数性质。因此本节给出以下预备知识:
(1)离散对数问题

(2)Hash函数具有的性质
(i)对于任意的消息x,计算h(x)是容易的;
(ii)寻找2个不同消息x和x*,使得h(x)=h(x*)在计算上是不可行的。
2 基于离散对数的盲签名方案
本节首先给出基于离散对数的盲签名方案的构造过程,方案具体描述如下。
2.1 初始化阶段

2.2 盲签名和签名验证阶段



(4)消息拥有者进行脱盲,得到
则消息m的签名为(m,r,s)。
(5)签名验证者收到签名(m,r,s)后,计算h=H(m,r),然后验证等式gs=yrrhmodp是否成立,若成立,则说明签名有效;否则签名无效。
2.3 安全性分析
本节从方案的正确性、盲性、不可链接性、不可伪造性等方面分析上述方案的安全性。
2.3.1 正确性分析
验证等式gs=yrrhmodp的正确性

gxrgkhagch=(gx)r(gka+c)h=yrrh。
2.3.2 盲性分析

2.3.3 不可链接性分析
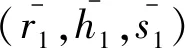
(1)
(2)
(3)
上述论证表明不论合法消息的签名对与任意的一组中间数据是否对应,验证等式都成立,从而说明验证等式成立时,签名人也不能将中间信息与消息签名对联系起来,即满足不可链接性。
2.3.4 不可伪造性分析


gs*=yr*(r*)h*modp,
然后挑战者在此基础上可伪造一个消息m=s*的ElGamal签名(m,γ,δ),其中
γ=r*,δ=h=H(m,γ)。
从而可将本方案的安全性规约到ElGamal签名方案的安全性上,由于ElGamal签名方案在离散对数困难问题假设下是安全的,所以本方案在离散对数困难问题假设下也是安全的。
概率分析:要使得攻击成功,须满足以下条件:

(2)攻击者以ε的概率生成一个有效且没有被询问过的签名(m*,r*,s*)。
2.3.5 效率分析
令P,Te,Ti,Tm分别表示一个双线性对,一次模幂,模逆和模乘运算所需要的时间,将新方案与现有方案进行比较(表1):

表1 本文算法与已有算法比较Tab. 1 Comparison between the proposed algorithm and the existing algorithms
由表1可以看出:文献[10-12]均含有双线性对运算,文献[9]虽然不含双线性对运算,但比本文方案运算量更大,其在签名与验证的整个过程中含有10个模幂、5个模逆以及19个模乘运算,而本文方案仅含有6个模幂、2个模逆以及10个模乘运算,从而本文方案是更加高效的。
3 代理盲签名方案及其分析
在上述盲签名方案的基础上,结合代理签名技术,本文提出了一种代理盲签名方案。
3.1 代理盲签名方案
3.1.1 参数生成阶段

3.1.2 代理授权阶段
UA=grA,VA=H2(mw,UA)xA+rA。
将(mw,UA,VA)通过安全信道发送给代理签名人B,B收到(mw,UA,VA)后验证
等式成立则计算代理秘钥为
SB=H2(mw,UA)xB+VA。
3.1.3 代理盲签名阶段

从而得到消息m的签名为(m,mw,UA,r,s)。
3.1.4 签名验证阶段
签名验证者收到签名(m,mw,UA,r,s)后,计算h=H1(m,r),然后验证等式
是否成立,若成立,说明签名有效,否则签名无效。
3.2 代理盲签名方案的分析
3.2.1 正确性分析
3.2.2 代理盲签名的可区分性
在代理盲签名的验证等式
中,同时有原始签名人和代理签名人的公钥yA,yB,还有代理授权的Hash函数H2(mw,UA),因此任何一个签名验证者都可以判断该签名是代理盲签名还是一般的盲签名方案。从而签名满足代理盲签名方案的可区分性。
3.2.3 代理盲签名方案的不可伪造性
定理2在代理授权阶段,如果离散对数问题是难解的,那么代理授权是不可伪造的。
证明假设伪造者为代理签名人,因为如果他不能伪造代理授权,则其他人更不能伪造代理授权。
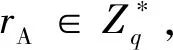
定理3在代理签名阶段,如果离散对数问题是难解的,那么代理签名是不可伪造的。
证明在代理盲签名方案中,首先代理秘钥是不可伪造的,因为即使是原始签名人,他虽然知道代理授权但是不知道代理签名人的私钥,因而不能伪造代理秘钥。其次代理盲签名阶段是用代理签名人的代理秘钥以及随机选择的参数进行盲签名的,与上述介绍的盲签名方案一样,因而具有相同的性质。不可伪造性的证明同定理1。
定理4代理盲签名方案满足盲签名方案的所有特性。
证明代理盲签名方案是在盲签名方案的基础上增加代理签名技术而得出来的,所以同样满足盲签名方案的盲性、不可链接性等特性。证明同盲签名方案中的证明类似。
4 总结
通过对现有方案的分析,提出了一种更加安全且高效的基于离散对数的盲签名方案,并对其进行了盲性、不可链接性和不可伪造性以及效率分析,并在此基础上结合代理签名技术提出了一种代理盲签名方案,最后对其进行了正确性、可区分性以及不可伪造性分析。

