城市污水处理过程动态多目标智能优化控制研究

韩红桂 张 璐 卢 薇 乔俊飞

城市污水处理过程(Municipal wastewater treatment process，MWWTP)包含初沉池、曝气池、二沉池等多个流程，是一个由多个流程组成的典型工业系统[1-2].各个流程紧密联系且相互影响.城市污水处理同时包含物理、化学和生物等反应过程，是一个复杂的动态操作过程[3].同时，城市污水处理运行过程受到多种动态性能指标的约束[4].因此，如何实现城市污水处理过程优化运行仍是一个亟待解决的难题[5-6].

优化控制方法通过设计合适的优化策略和控制策略，实现性能指标的最优化，已在城市污水处理过程中得到了广泛的应用[7-8].然而，实施城市污水处理优化控制的过程中面临两个问题:如何设计城市污水处理运行过程的性能指标和如何实现性能指标的优化.

为了描述城市污水处理过程出水水质指标，Jeong 等[9]提出了一种基于城市污水处理标准机理模型的出水化学需氧量预测模型，该模型能够描述城市污水处理过程出水化学需氧量与溶解氧浓度、温度、氧化还原电位等过程变量之间的关系.实验结果显示所提出的出水化学需氧量预测模型具有较高的精度.此外，Xie 等[10]设计了一种基于活性污泥数学模型的出水水质预测模型，用来获取出水有机物浓度与固体停留时间和内循环之间的相关关系.结果表明所提出的出水水质模型能够准确地获取城市污水处理过程出水水质特性.为了同时实现对城市污水处理过程能耗指标和出水水质指标的描述，Alsina 等[11]提出了一种基于机理反应模型的污水处理过程性能综合评价模型，用于描述能耗、出水水质等性能指标与溶解氧浓度、固体悬浮物浓度等过程变量之间的关系.实验结果表明基于多指标的性能评价模型能够准确地获取污水处理过程的动态特性，从而提高污水处理过程的运行效率.Yang 等[12]通过深入分析污水处理过程计算流体动力学模型，建立了一种污水处理过程运行性能评价预测模型，该性能评价预测模型能够表达能耗、出水水质与入水流量、溶解氧浓度等过程变量之间的关系.结果表明所提出的性能评价预测模型能够准确地表达能耗和出水水质的动态特性.但是，基于机理模型的性能指标模型参数较多，难以保证模型精度[13-14].

为了解决性能指标模型精度的问题，Asadi等[15]通过分析城市污水处理过程的机理和运行数据的特征，建立了一种基于神经网络的曝气能耗模型，该模型的输入变量是入水流量、溶解氧浓度、固体悬浮物浓度等过程变量，输出变量是污水处理过程生化反应过程的曝气能耗.实验结果表明所建立的曝气能耗模型能实时反映运行过程变量与能耗之间的关系.为了同时考虑多个性能指标，Durrenmatt等[16]提出了一种基于自组织映射的城市污水处理能耗和出水水质评价模型，通过机理和数据相结合建立了性能指标与关键过程变量的关系.实验结果表明所提出的基于自组织映射的能耗和出水水质评价模型能够准确获取系统运行状态.此外，丛秋梅等[17]通过分析生化反应过程运行机理和过程数据，提出了一种基于递阶神经网络的污水处理过程评价模型，该模型能够获得出水化学需氧量浓度、出水悬浮物固体浓度、出水氨氮浓度等与各组分浓度之间的关系.实验结果表明该性能指标模型可实现对城市污水处理运行过程的实时评价.然而，城市污水处理过程同时包含多个反应单元和动态的操作指标，如何根据城市污水处理运行过程设计包含多个反应单元的动态性能指标模型仍然是一个具有挑战性的任务[18-19].

如何设计优化算法实现对性能指标的优化是实施城市污水处理过程优化控制的另一个关键因素[20-21].针对城市污水处理过程多个冲突目标的优化问题，Vega 等[22]提出了一种基于序列二次规划的分层优化控制方法，利用基于权重系数的序列二次规划方法来优化能耗和出水水质模型，获取溶解氧和硝态氮的优化设定值，并利用PID 控制策略对优化设定值进行控制.实验结果表明该方法能够有效提高操作性能，能够在保证出水水质达标的条件下降低运行能耗.此外，Schluter 等[23]提出了一种基于扩展蚁群优化算法的优化控制策略，通过该优化策略权衡经济成本和操作性能，获取被控变量优化设定值，并利用PI 控制器完成对设定值的控制，保证城市污水处理过程的优化运行.虽然上述优化控制策略能够提高城市污水处理过程的操作性能，但其本质都是将多目标优化问题通过权重系数转化为单目标优化问题.由于城市污水处理过程中的非线性和时变性等特点，难以获取合适的权重参数[24-25].为了解决城市污水处理过程的多目标优化控制问题，Guerrero等[26]提出了一种多准则的优化控制策略，通过同时优化运行能耗和出水水质获得合适的溶解氧和硝态氮优化设定值，并利用PI 控制器完成对设定值的控制.实验结果表明该优化控制策略能够提高操作性能，不仅改善了出水水质，而且降低了能耗.为了进一步提高优化控制策略的性能，保证优化设定值的有效性，Beraud 等[27]提出了一种基于自适应多目标微分进化算法的智能多目标优化控制方法，利用自适应多目标微分进化算法同时优化能耗和出水水质，获得溶解氧和硝态氮的优化设定值，并通过智能控制器完成对优化设定值的控制.实验结果表明该方法能够获得一组有效的优化设定值，提高城市污水处理过程的优化控制性能.此外，Yen 等[28]提出了一种基于动态多种群的多目标粒子群优化算法，利用动态的种群策略和目标空间压缩与扩展策略来管理群内和群体间的信息交互，在搜索过程中逐步利用目标空间.结果表明，该方法能够获得满意的优化解.此外，许多学者提出了不同的动态多目标优化控制策略来提高城市污水处理过程的操作性能[29-31].然而，由于城市污水处理过程是一个复杂的动态非线性系统，存在着多个时变的目标函数，如何根据时变的优化目标设计一种动态多目标优化控制策略来获得合适的优化解仍是一个急需解决的难点问题[32-33].

为了实现城市污水处理过程的优化控制，提高运行性能，本文提出了一种城市污水处理过程动态多目标智能优化控制(Dynamic multiobjective intelligent optimal control，DMIOC)策略.与其他优化控制策略相比，所提出的DMOIC 策略的优势为:

1) 建立了一种基于自适应核函数的动态性能指标模型，能够实现对关键性能指标曝气能耗、泵送能耗和出水水质的准确描述.

2) 设计了一种基于自适应飞行参数调整机制的动态多目标粒子群优化算法 (Dynamic multiobjective particle swarm optimization，DMOPSO)，通过飞行参数的自适应调整有效平衡粒子的多样性和收敛性，从而获得合适的溶解氧和硝态氮优化设定值.

3) 采用了一种多回路PID 控制策略，实现对溶解氧和硝态氮优化设定值的控制.

1 城市污水处理过程动态特性分析

在城市污水处理过程中，活性污泥法是最常用的处理方法.活性污泥反应过程由生化反应池和二次沉淀池组成，利用活性污泥的生物凝聚、吸附和氧化作用，以分解去除污水中的有机污染物.然后使污泥与水分离，大部分污泥再回流到曝气池，多余部分则排出活性污泥系统.因此，城市污水处理过程是一个复杂的动态系统，具有以下运行特点:

1) 城市污水处理过程是一个动态变化的过程，其反应过程随着入水流量、微生物活性等的变化而变化.

2) 城市污水处理运行过程同时包含多个动态性能指标，如曝气能耗、泵送能耗和出水水质等，其性能指标的运行状态随着反应过程的变化而实时调整，其优化调整周期为2 个小时.同时，各性能指标之间相互影响且相互冲突.

3) 城市污水处理过程合适的被控变量优化设定值能够保证出水水质达标排放，提高操作性能.

近年来，随着城市污水处理过程规模的增加和排放要求的日益严格，在保证出水水质的基础上降低能耗是非常必要的.研究城市污水处理过程动态多目标智能优化控制策略，同时考虑城市污水处理过程中的动态特性和多个冲突目标间的优化，可以有效地提高城市污水处理过程的操作性能.

2 动态多目标智能优化控制设计

为了有效平衡城市污水处理过程动态环境下多个冲突目标间的关系，本文提出了一种多目标智能优化控制方法——DMIOC.在DMIOC 中，为了准确获取城市污水处理过程中的动态特性，建立了一种基于自适应核函数的能耗和出水水质模型;同时，为了平衡能耗和出水水质之间的关系，设计了一种基于自适应飞行参数调整机制的DMOPSO 算法，用于获得合适的被控变量优化设定值.

2.1 动态多目标智能优化控制架构

本文设计了一种动态多目标智能优化控制架构(如图1 所示).该架构包含了基于自适应核函数的动态性能指标模型，泵送能耗(Pumping energy，PE)、曝气能耗(Aeration energy，AE)和出水水质(Effluent quality，EQ) 模型，用于获取系统动态特性;设定值的动态优化方法，利用基于自适应飞行参数调整机制的DMOPSO 算法来优化PE、AE和EQ 模型，获得被控变量溶解氧(Dissolved oxygen，SO) 和硝态氮(Nitrate nitrogen，SNO)的优化设定值;设定值的控制方法，通过多回路PID 控制策略完成对SO和SNO优化设定值的控制.此外，实验平台为国际水协与欧盟科学技术合作组织联合开发的活性污泥污水处理基准仿真模型(Benchmark simulation model No.1，BSM1).

2.2 动态性能指标模型的建立

城市污水处理运行过程的主要目标是在保证出水水质达标的同时降低操作能耗.准确描述城市污水处理过程动态性能指标PE、AE 和EQ 是提升操作性能的关键.城市污水处理过程性能指标PE、AE 和EQ 动态调整周期为2 个小时，因此，在每个优化周期应实时获取性能指标的动态特性.本文通过分析城市污水处理过程的动态特性和运行数据，获取与PE、AE 和EQ 相关的过程变量，分别为入水流量Qin、SO、SNO、氨氮(Ammonia nitrogen，SNO)和悬浮物固体浓度(Suspended solids，SS).根据分析的相关过程变量，利用自适应核函数方法建立PE 与相关过程变量间的动态关系f1(·)、AE与相关过程变量间的动态关系f2(·) 和EQ 与相关过程变量间的动态关系f3(·)，其表达式为

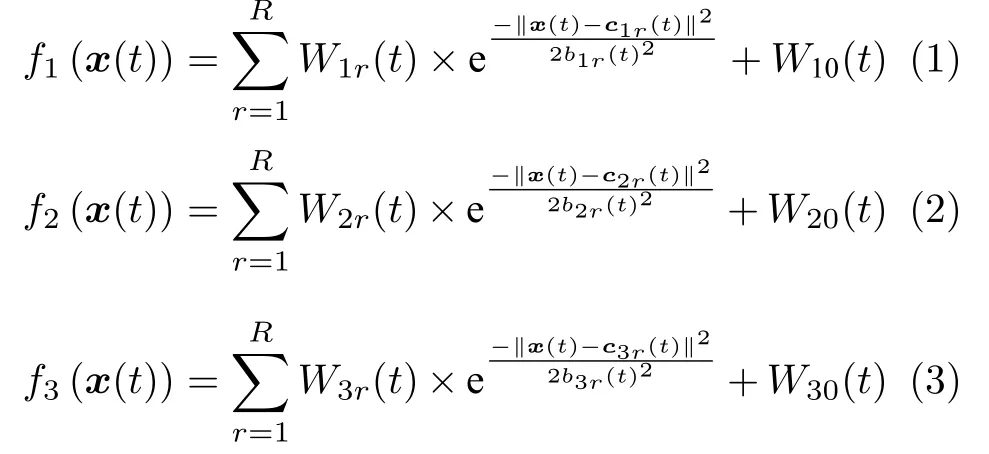
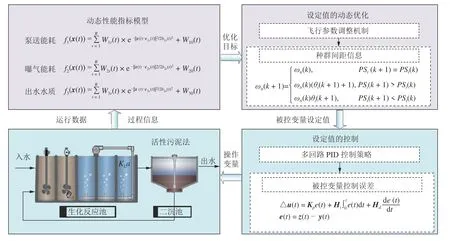
图1 城市污水处理过程动态多目标智能优化控制架构Fig.1 The scheme of DMIOC for municipal wastewater treatment process

其中，f1(x(t))为t时刻PE 模型，f2(x(t))为t时刻AE 模型，f3(x(t))为t时刻EQ 模型.x(t)为t时刻的输入变量，x(t)=[Qin(t)，SO(t)，SNO(t)，SNH(t)，SS(t)].c1r(t)，c2r(t)，c3r(t) 分别为t时刻PE，AE 和EQ 模型中第r个核函数的中心，b1r(t)，b2r(t)，b3r(t)分别为t时刻PE，AE 和EQ 模型中第r个核函数的宽度，W1r(t)，W2r(t)，W3r(t) 分别为t时刻PE，AE 和EQ 模型中第r个核函数的连接权值，W10(t)，W20(t)，W30(t) 分别为t时刻PE，AE 和EQ 模型的偏置，r=1，2，···，R，R为核函数的个数.

基于自适应核函数的城市污水处理过程PE、AE 和EQ 模型，不仅可以根据实际输出与期望输出之间的误差对性能指标模型参数进行自适应调整，保证性能指标模型的准确性;同时，所提出的性能指标模型建立了PE、AE 和EQ 与关键被控变量SO和SNO之间的关系，有利于实现城市污水处理过程动态多目标智能优化控制.

2.3 设定值的动态优化

为了同时优化动态性能指标PE、AE 和EQ，获得被控变量优化设定值，将已建立的t时刻PE 模型f1(x(t))、AE 模型f2(x(t))和EQ 模型f3(x(t))作为优化目标函数，利用基于自适应飞行参数调整机制的DMOPSO 算法对其进行优化，其优化目标函数F(t)为

2.4 设定值控制

3 实验结果及分析

将所设计的DMOPSO 算法和DMIOC 策略应用于基准测试函数和基准仿真平台BSM1，验证方法的有效性.通过收敛性指标 GD和多样性指标SP对所设计的DMOPSO 算法进行评价，将设计的DMOPSO 算法与其他优化算法(pccsAMOPSO[31]，clusterMOPSO[33]，NSGA[29])进行比较，验证所设计的DMOPSO 算法的有效性.

为了保证算法比较的公平性，其他对比优化算法的参数保持与原文相同.同时，将提出的DMIOC 与其他优化控制策略进行对比，验证DMIOC 的性能.此外，利用绝对误差积分(Integral of absolute error，IAE)来评估控制性能:

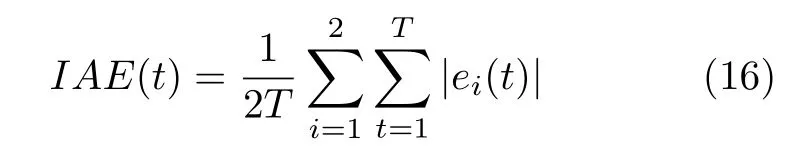
其中，T是样本总数，e1(t)和e2(t)分别为SO和SNO实际输出和优化设定值的误差.

图2 给出以动态性能指标模型PE、AE 和EQ作为优化目标函数进行优化时第6 天第1 次4 种优化算法的效果图.从图中可以看出，与pccsAMOPSO[31]、clusterMOPSO[33]和NSGA[29]相比，DMOPSO 算法的优化解分布更加均匀.具体的指标如表1 所示.

图2 不同优化算法的逼近效果Fig.2 The approximation effect of different optimization algorithms

表1 给出不同优化算法在ZDT3、ZDT4、DTLZ2、DTLZ7 四个测试函数中的优化性能结果.从对比结果可以看出，所提出的DMOPSO 算法可以在ZDT3和DTLZ2 函数中获得最小的SP 值，在ZDT4 和DTLA7 函数中可以获得最小的GD 和SP 值.这些结果表明，本文所设计的DMOPSO 算法可获得多样性和收敛性性能更佳的优化解.

表2 给出不同优化算法在不同测试函数中的计算时间，在ZDT3 和ZDT4 函数中，所提出的DMOPSO 方法具有最少的计算时间，在DTLZ2和DTLA7 函数中计算时间与用时最少的Cluster-MOPSO 算法相比相差较少，结果表明，本文提出的DMOPSO 算法能够快速收敛到Pareto 前沿.

图3 给出4 种不同的优化控制方法获得的平均PE 值.实验结果显示，与clusterMOPSO-OC，pccsAMOPSO-OC 和NSGA+PI-OC 相比，所提出的DMIOC 策略可以获得最小的平均PE 值.图4给出4 种优化控制算法获得的平均AE 值，从图中可以看出，所设计的DMIOC 策略能够有效地降低AE，减少曝气操作成本.图5 给出4 种不同优化控制算法的平均EQ 值，除第10 天和第11 天之外，DMIOC 策略可以在12 天内获得最优的EQ 值.为了进一步验证所提出方法的有效性，将DMIOC 与其他优化控制策略进行对比，具体结果如表3 所示.

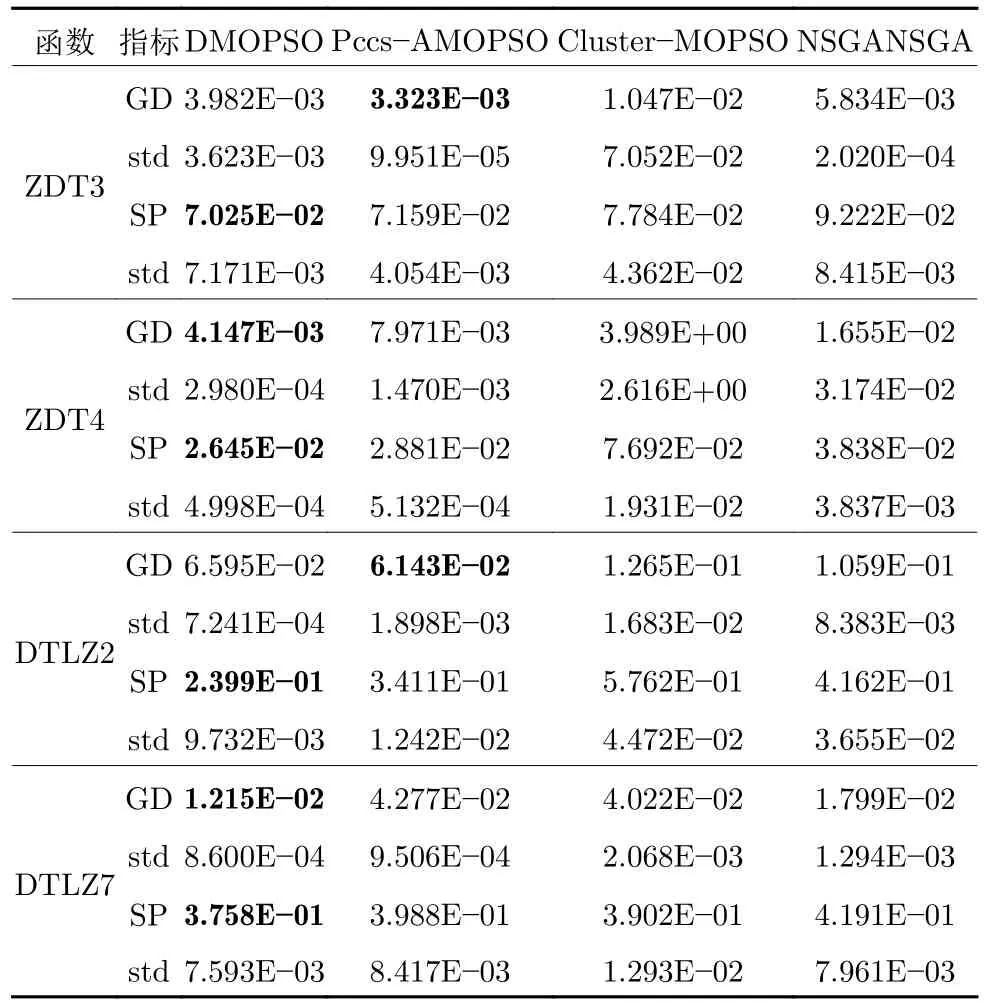
表1 不同优化算法的性能比较Table 1 The approximation effect of different optimization algorithms

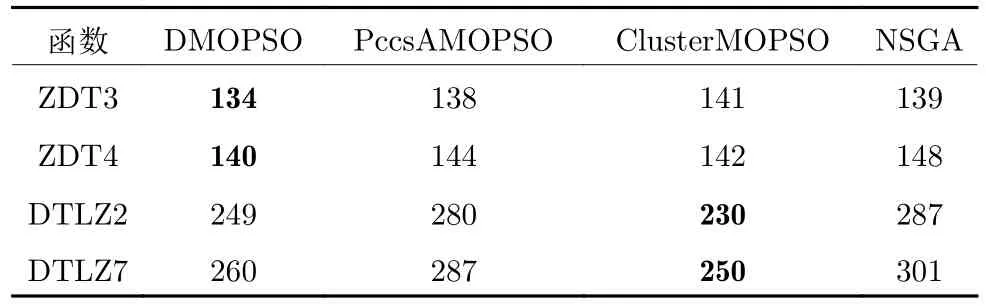
表2 不同优化算法的计算时间比较 (s)Table 2 Calculation time comparison of different optimization methods (s)

表3 给出4 种不同优化控制算法的优化结果对比.从结果可以看出，DMIOC 策略得到的平均AE和PE 值分别为249 kW·h 和3 630 kW·h，其操作能耗(PE 和AE 之和)小于其他优化控制策略.同时，平均EQ 值为6 616 kg poll，小于其他对比的优化控制策略.结果表明，所提出的DMIOC 策略能有效地降低污水处理过程操作能耗，改善出水水质.同时，结果验证了所提出的DMIOC 策略能够有效地应用于城市污水处理过程.

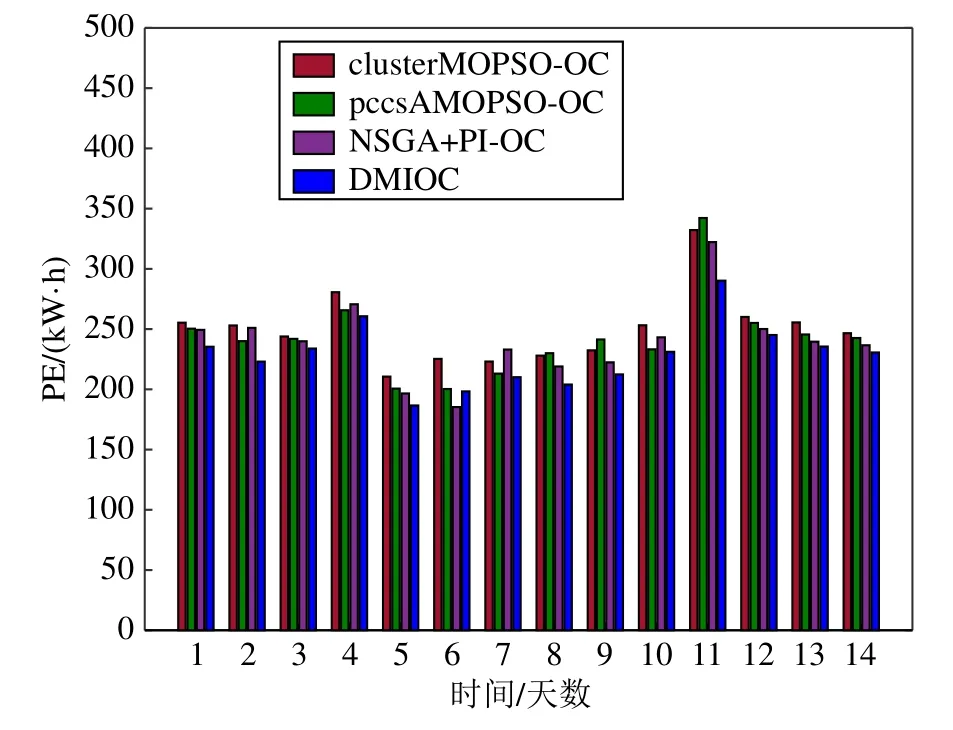
图3 平均PE 值Fig.3 Average values of PE

图4 平均AE 值Fig.4 Average values of AE

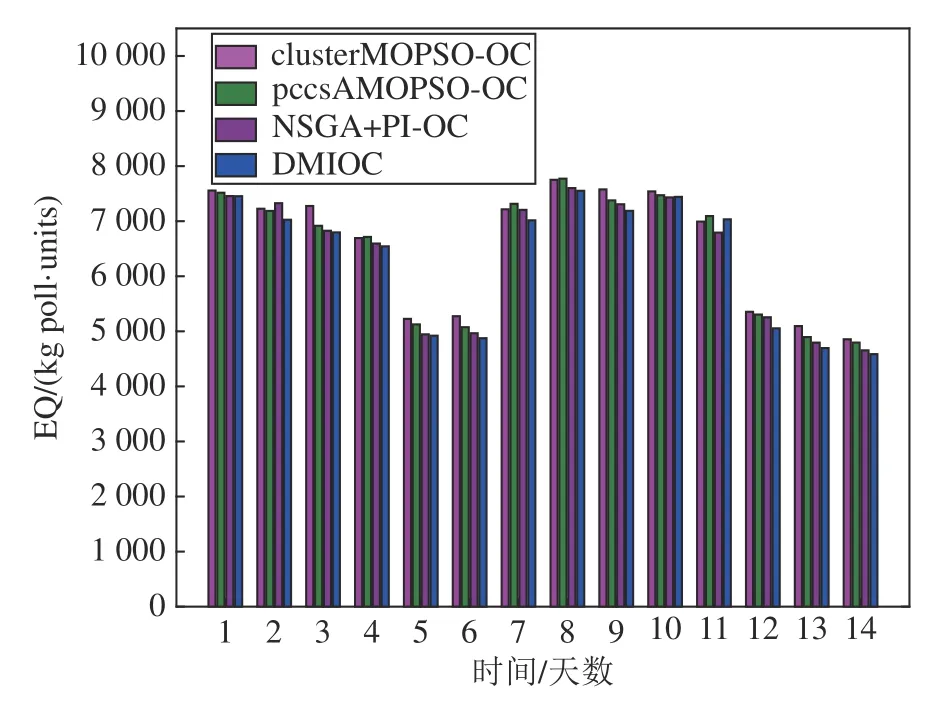
图5 平均EQ 值Fig.5 Average values of EQ

图6 和图7 分别给出被控变量SO和SNO的控制效果图.图6 为SO的控制结果图，其中，实线为通过DMOPSO 获得的SO优化设定值，虚线为通过多回路PID 控制策略获得的SO实际输出.从图6可以看出，所提出的DMIOC 策略能较好地跟踪优化设定值.图7 给出SNO的控制效果，其中，实线为通过DMOPSO 获得的SNO优化设定值，虚线为通过多回路PID 控制策略获得的SNO实际输出.从图中可以看出，DMIOC 能以较小的误差实现控制.控制误差结果如图8 所示，SO跟踪误差范围为±0.25 mg/l，SNO控制误差范围为 ±0.58 mg .上述实验结果表明，所提出的DMIOC 策略能够实现对被控变量SO和SNO优化设定值的控制.

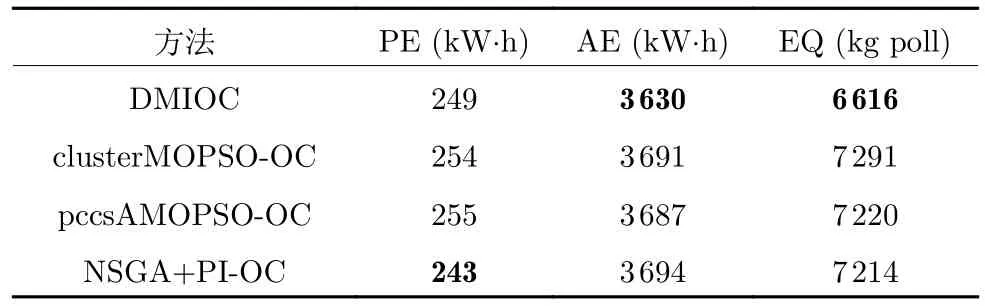
表3 不同优化控制方法优化性能比较Table 3 Comparison of optimization performance of different optimal control methods

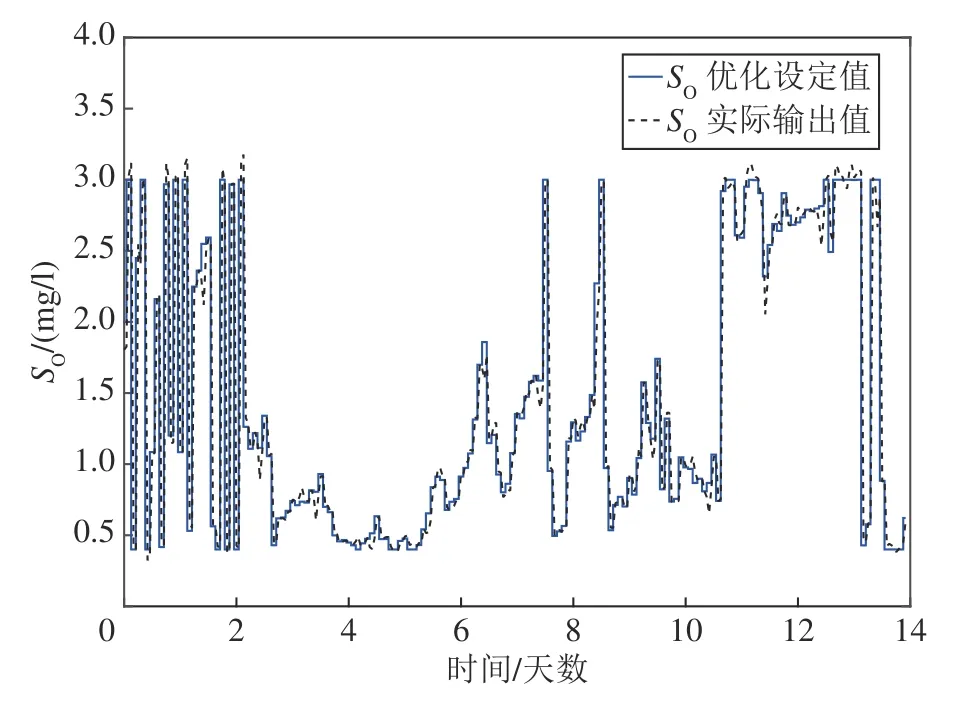
图6 SO的控制效果Fig.6 Control results of SO

为了进一步验证所提出方法的控制性能，将DMIOC 策略与其他优化控制策略进行对比，具体结果如表4 所示.表4 给出4 种不同优化控制算法DMIOC，clusterMOPSO-OC，pccsAMOPSO-OC和NSGA+PI-OC 的控制性能比较结果.从表4可以看出，所提出的DMIOC 策略能够获得较好的控制效果，IAE为 0.097 mg/l，低于其他几种对比的优化控制算法.同时，出水氨氮SNH和出水悬浮物浓度SS的值分别为 3.08 mg/l和 12.15 mg/l，均小于其他优化控制策略的出水有机物浓度.实验结果表明，所提出的DMIOC 策略能够获得有效的溶解氧和硝态氮优化设定值.同时，该方法能够保证控制效果，降低出水有机物浓度.因此，所提出的DMIOC 适用于城市污水处理过程.

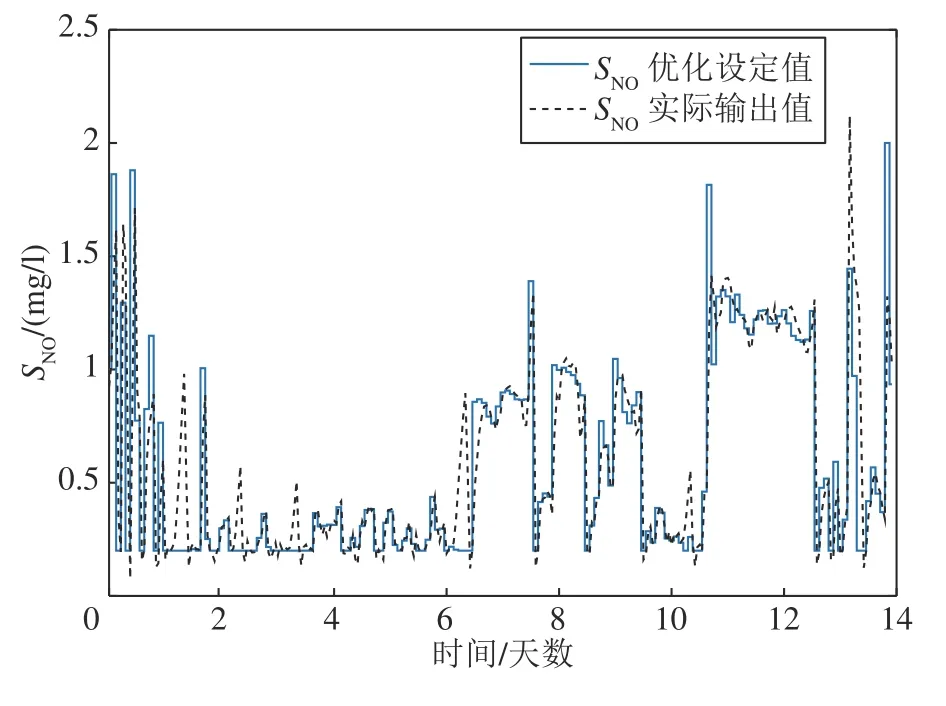
图7 SNO的控制效果Fig.7 Control results of SNO

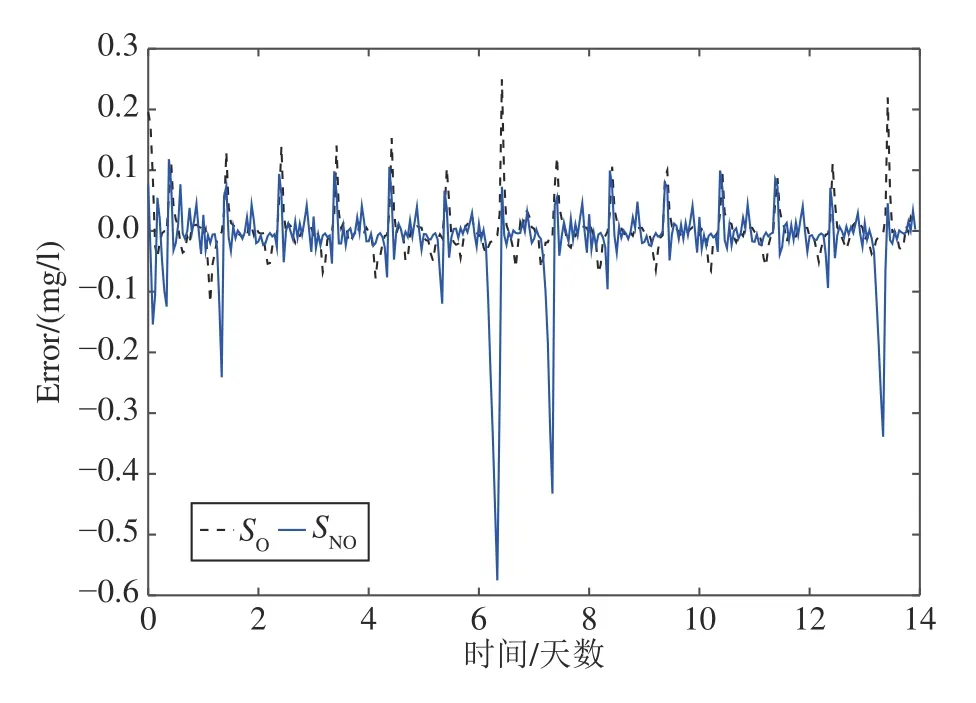
图8 SO和 SNO的误差值Fig.8 Control errors of SO andSNO

表4 不同优化控制方法控制性能比较Table 4 Comparison of control performance of different optimal control methods

4 总结与展望

针对城市污水处理过程优化控制问题，本文提出了一种城市污水处理过程多目标智能优化控制策略.在该策略中，利用自适应核函数方法获取城市污水处理过程的动态特性，通过基于自适应飞行参数调整机制的动态多目标粒子群优化算法获得优化设定值.根据实验结果及分析得到以下结论:

1) 基于自适应核函数的泵送能耗、曝气能耗和出水水质模型能够根据城市污水处理过程运行状态进行动态调整，实现对城市污水处理过程关键性能指标的准确描述.

2) 基于自适应飞行参数调整机制的动态多目标粒子群优化算法，能够平衡种群的全局探索能力及局部开发能力，同时优化城市污水处理过程泵送能耗、曝气能耗和出水水质多个冲突目标的关系，获得有效的溶解氧和硝态氮优化设定值.

3) 通过多回路PID 控制策略能够实现对动态优化设定值的控制，保证城市污水处理过程的稳定运行.所提出的DMIOC 策略可以取得较好的优化效果和控制效果，结果表明该方法适用于城市污水处理过程.

虽然本文提出的城市污水处理过程多目标智能优化控制策略能够取得较好的效果，但仍有一些方面需要改进.在应用优化控制策略时，对城市污水处理过程关键性能指标动态特性的准确获取尤为重要，而关键性能指标由于其反应过程的不同，反应时间尺度亦不相同.如何将不同的时间尺度特点考虑到动态特性获取过程中，进一步提高城市污水处理过程优化控制性能仍然是一个需要解决的难题.