异步悬浇施工中波形钢腹板局部变形研究
彭东林,杨建荣,郑晓龙
异步悬浇施工中波形钢腹板局部变形研究
彭东林,杨建荣,郑晓龙
(昆明理工大学 建筑工程学院,云南 昆明 650500)
为准确计算波形钢腹板连续刚构桥在异步悬浇施工过程中的局部变形。通过有限元软件Midas/FEA建立了板壳单元模型,研究了波形钢腹板在荷载作用下的局部变形,对比现场实测数据,分析了计算值与实测值的误差变化规律。研究结果表明:异步施工过程中的波形钢腹板局部变形主要来源于荷载的影响,根据误差变化规律拟合出挠度关系式,对施工中的波形钢腹板局部变形值进行修正,以保证成桥线形达到设计要求。
波形钢腹板;悬臂施工;连续刚构桥;异步施工;局部变形
随着波形钢腹板PC组合箱梁桥的逐步推广和建造,其施工方法也逐步成熟。德国Altwipfergrund桥首次使用异步悬浇施工进行波形钢腹板PC组合箱梁桥的建设[1]。异步悬浇施工法是基于悬臂施工法的改进施工法,以波形钢腹板作为梁段悬臂施工过程中的承重支架,承受挂篮自重和混凝土湿重,使挂篮更简单、更轻便,相邻节段的混凝土顶板、底板同时浇筑,提高了施工效率[2]。波形钢腹板的安装定位对桥梁线形影响大。施工过程中,通过设置预抬值,抵消施工期的位移和成桥后运营期间的结构下挠,确保成桥后线形达到设计要求。施工期间,位移主要由挂篮弹性变形、主梁整体下挠及钢腹板局部变形叠加组成[3−4]。异步悬浇施工与传统悬臂施工的区别为混凝土顶、底板的异步浇筑,波形钢腹板作为承重支架。其变形与传统悬臂施工过程中的变形存在明显差异,而异步悬浇施工中的钢腹板局部变形难以通过计算控制。为保证施工中波形钢腹板立模标高的准确性,必须了解异步悬浇施工中波形钢腹板局部变形规律。
诸多学者对异步悬浇施工中波形钢腹板的受力性能和变形规律进行了研究。郑尚敏[5]等人通过分别建立三维实体模型与梁单元模型,研究波形钢腹板PC组合梁桥在施工过程中不同施工阶段和不同施工荷载作用下,分析剪切变形对其挠度的影响。发现在自重和外荷载作用下,最大悬臂施工阶段剪切产生的挠度占总挠度的30%~40%。邓文 琴[6]等人通过波形钢腹板箱梁桥异步施工阶段足尺模型试验,得出等效施工荷载作用下的波形钢腹板两端挠度差达到5.13 mm,侧向变形值最大达到25 mm。岳宏智[7]等人建立了山东小清河特大桥上部结构精细化实体模型,发现悬臂施工过程中随着悬臂长度的增加,观测截面的总体下挠值增大,增幅也逐渐增大。易征[8]对某连续刚构桥跨中断面进行数值模拟,结果表明:当上、下游断面不同高程时,上游断面的三分力系数随着工况的变化呈规律性变化,下游断面受到强烈的尾流干扰和遮挡效应。因此,桥梁气动干扰效应对位移的影响不容忽视。
当前的研究更多集中于波形钢腹板异步悬浇施工中的受力性能和整体挠度,针对波形钢腹板局部变形的研究较少。连续刚构桥施工中,常遇到波形钢腹板局部下挠过大的问题。因此,本研究以某在建桥梁的波形钢腹板为研究对象,拟采用Midas/ FEA有限元软件建立板壳单元模型,计算施工荷载作用下波形钢腹板的局部变形。根据现场实测数据,对敏感参数进行相关性分析,得出波形钢腹板局部变形值修正公式。解决施工中产生的局部变形过大的问题,保证成桥线形达到设计要求。
1 工程概况
某连续刚构桥采用(65+4×120+65) m跨径布置,主梁为单箱单室波形钢腹板组合箱梁,箱梁顶板宽10.55 m,底板宽6.5 m;中墩支点梁高7.5 m,底板厚80 cm;边跨支点及跨中梁高3.5 m,底板厚28 cm,梁高和底板厚度均按二次抛物线变化;腹板采用1600型波形钢腹板[9],板厚为14~22 mm;混凝土采用C55,波形钢板采用Q345qc钢。
为了缩短工期,提高施工效率,主桥上部结构采用异步悬浇施工。主梁节段划分为15段,合拢前节段划分为14.4 m(0#、1#节段)+3.2 m(2#节段)+ 10×4.8 m(3#~12#节段),中跨合拢段长3.2 m,边跨合拢段长1.6 m,边跨现浇段长4.8 m,节段划分示意图如图1所示。
该桥中跨和边跨悬臂施工过程可划分为13个施工阶段,除0#、1#节段及13#合拢段外,每一施工阶段的标准步骤为:①移动挂篮至第节段;②绑扎第节段底板和第−1节段顶板普通钢筋;③浇筑第节段底板和第−1节段顶板混凝土;④混凝土养护,吊装第+1节段波形钢腹板,待混凝土达到强度后,张拉−1节段顶板预应力钢束;⑤挂篮前移,进入下一施工循环。异步悬浇施工流程如图2所示。
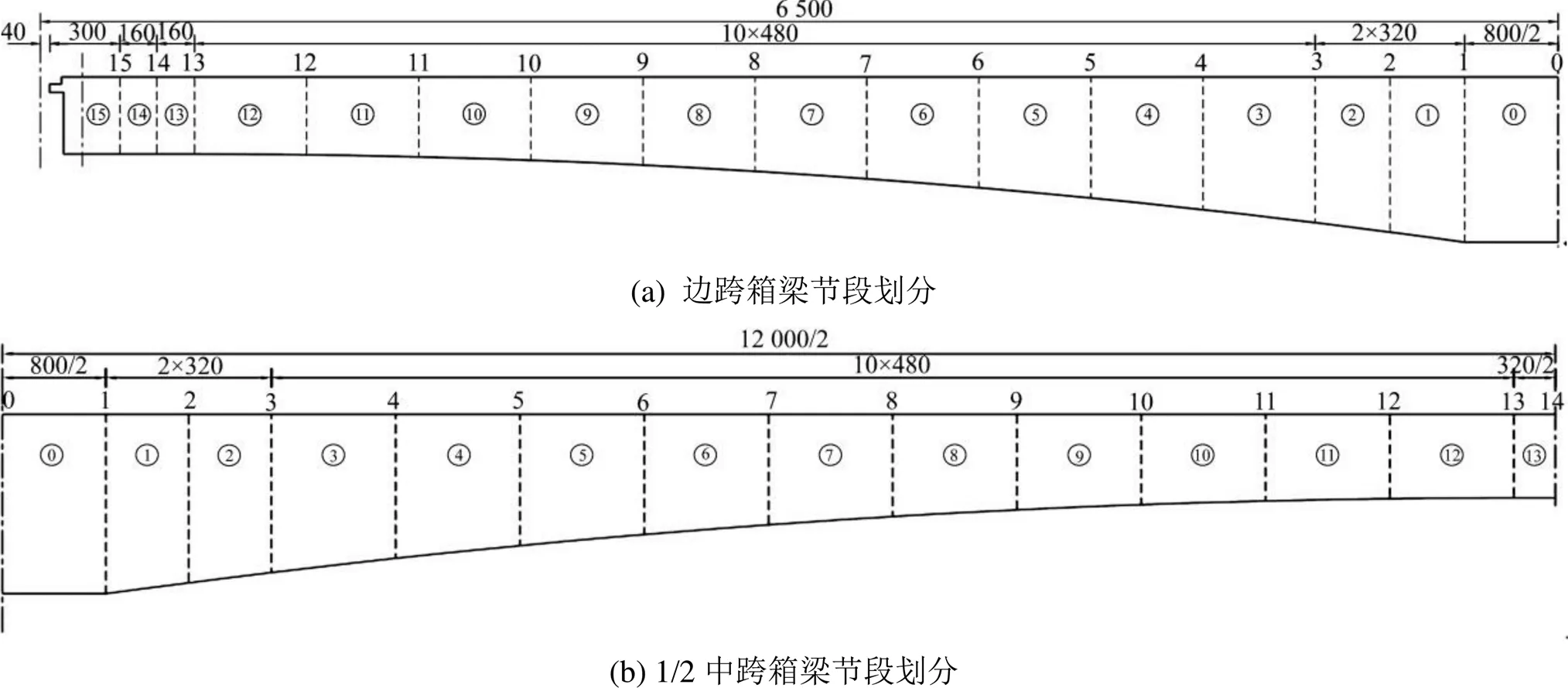
图1 箱梁节段划分(单位:cm)
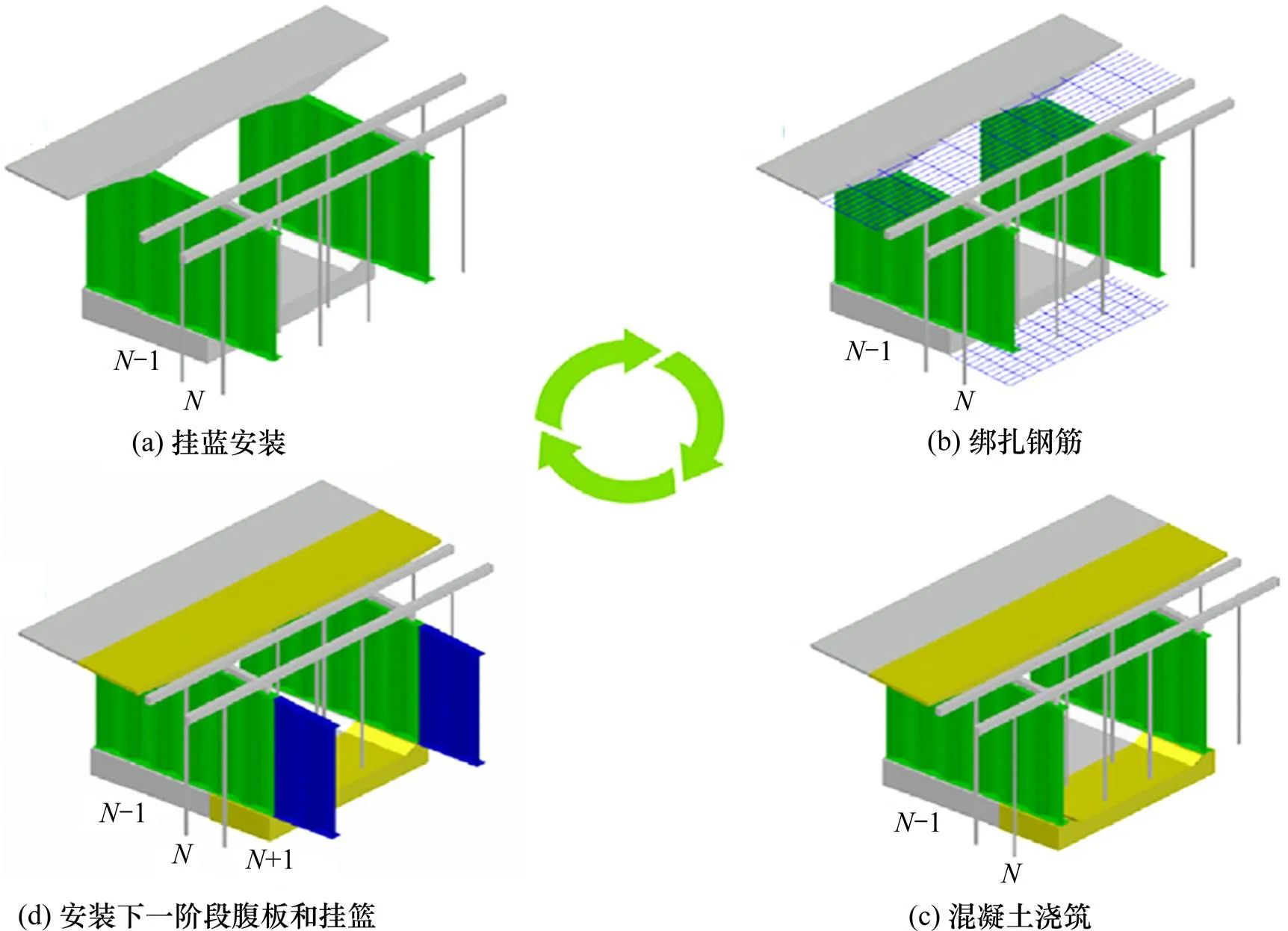
图2 异步悬浇施工流程
2 波形钢腹板局部变形计算
2.1 施工工况
混凝土板与钢梯形波纹腹板剪力重分布的主要因素是剪力效应,这是影响桥梁结构产生挠度的关键[10]。细化施工工况,有利于分析剪力效应,可更好地观察每个施工步骤的挠度值。对于第节段波形钢腹板,在标准异步悬浇施工循环中,按照所承受的荷载可划分为5个工况:
工况一:移动挂篮至第节段波形钢腹板;
工况二:浇筑第节段底板混凝土;
工况三:安装第+1节段波形钢腹板;
工况四:移动挂篮至第+1节段波形钢腹板;
工况五:浇筑第+1节段底板和第节段顶 板混凝土。
2.2 计算模型
选取第节段波形钢腹板,利用Midas/FEA有限元分析软件建立板壳单元模型,如图3所示,对异步悬浇施工中的波形钢腹板局部变形进行计算。其中,混凝土的顶板、底板采用实体单元模拟,波形钢腹板采用板单元模拟,临时横撑采用梁单元模拟,依次将板壳单元划分为200、100、50 mm的网格进行计算。分析结果表明:网格单元长度为100 mm的计算结果与50 mm的无差别,且100 mm网格划分的收敛性更好,所以本研究将网格单元的大小取为100 mm。波形钢腹板的上、下翼缘板和混凝土的顶板、底板在交界面上全部自由度耦合;已成形的第−1节段对第节段的约束条件为固结。

图3 Midas/FEA板壳单元模型
2.3 施工阶段计算挠度值
异步悬浇施工中,波形钢腹板受到的施工荷载包括:波形钢腹板自重、混凝土湿重、挂篮荷载。其中,混凝土湿重和挂篮自重均简化为集中力形式,作用于顶模后吊点、底模后吊点和挂篮前后支点。有限元计算结果见表1。
3 波形钢腹板局部变形分析
为研究异步悬浇施工中波形钢腹板的局部变形,在每一梁段的波形钢腹板上翼缘板中心点布置一变形测点,测点编号-1表示第节段第1测点。以波形钢腹板安装定位的高程值作为初始值,每一施工工况后的测量值与初始值的差值为绝对变形值,每一梁段波形钢腹板的绝对变形值与相邻前一节段的差值为该节段波形钢腹板的局部变形值。采用彭官友[11]提出基于累积法的GM(1,1)对桥梁进行监控,线性误差分析会大大减小。本研究选取2#节段、6#节段、11#节段三个关键节段的模型计算结果与现场实测值见表2。2#、6#、11#阶段的挠度值如图4~6所示,实线代表计算值,虚线代表实测值。
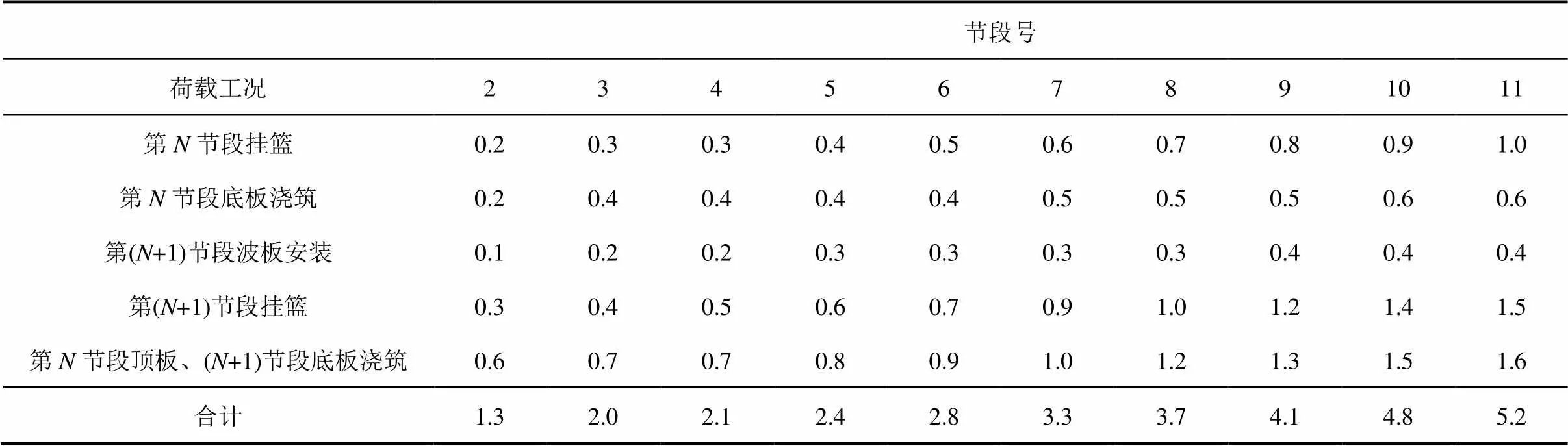
表1 FEA计算结果(单位:mm)
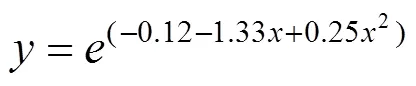
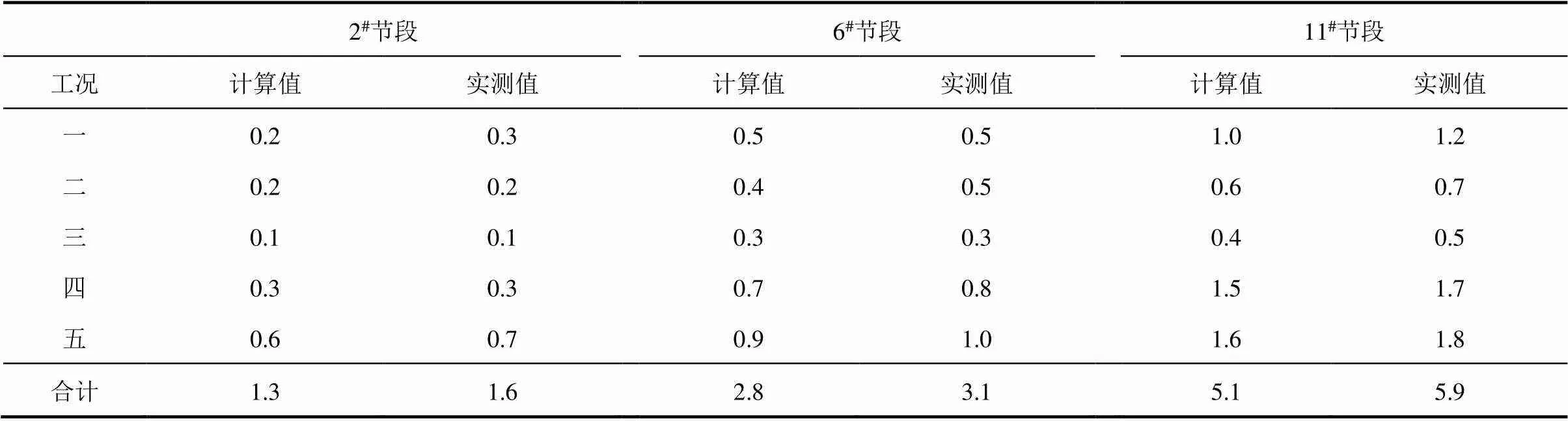
表2 5#墩第2、6、11节段波形钢腹板局部变形(单位:mm)
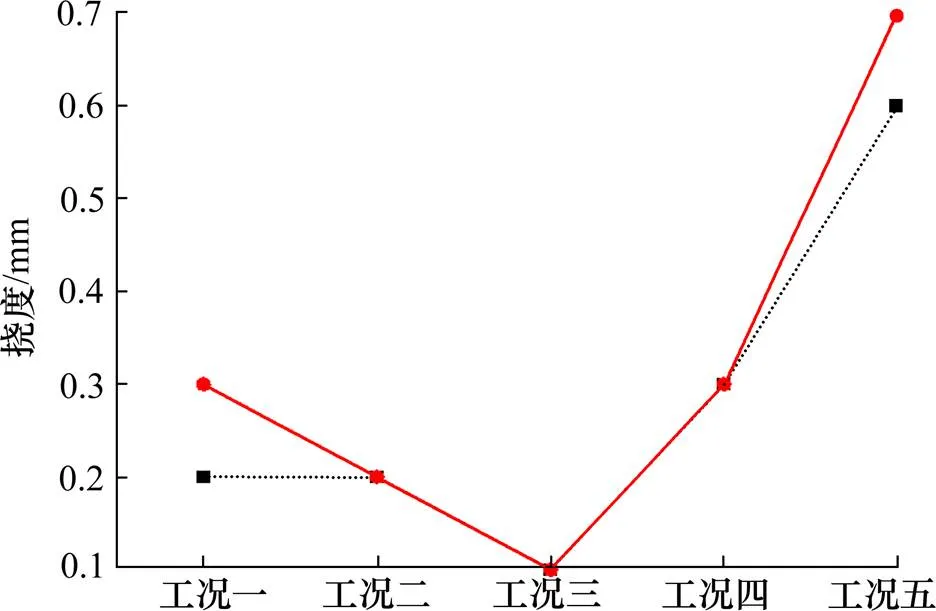
图4 2#节段挠度值
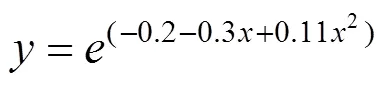
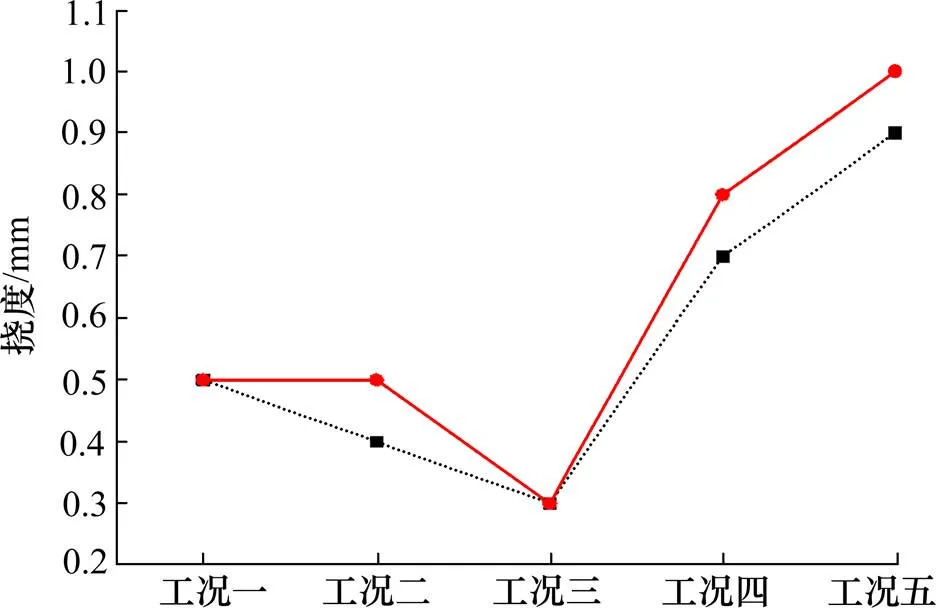
图5 6#节段挠度值
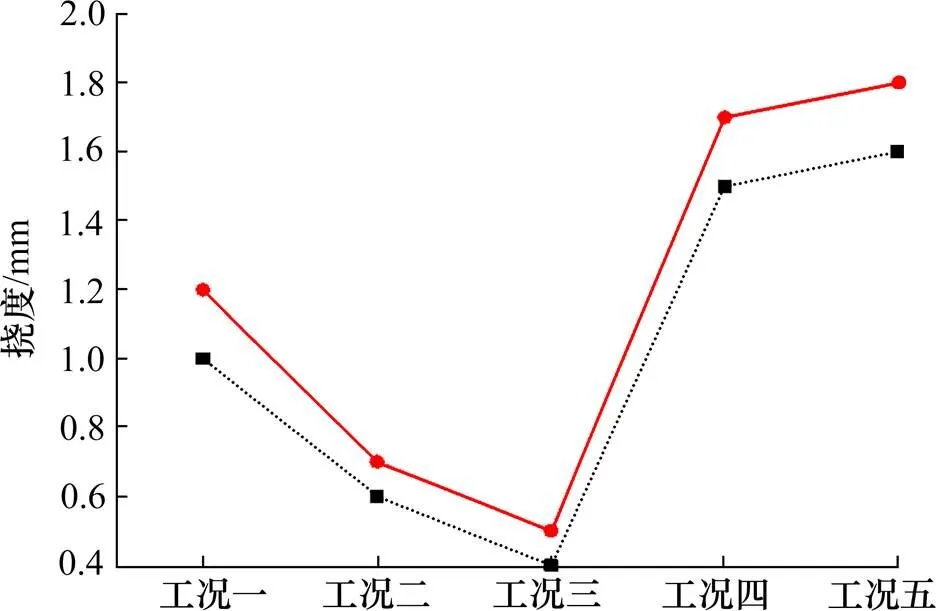
图6 11#节段挠度值
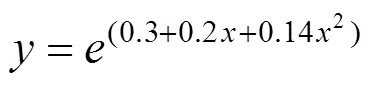
将实测结果与理论计算值进行对比,由工况二可以看出,浇筑混凝土底板引起的下挠值与理论计算值基本吻合,差值范围不超出1 mm。由工况三可以看出,下一节段波形钢腹板吊装时,波形钢腹板变形值极不稳定,部分出现上挠。安装波形钢腹板的过程中,为了调整波形钢腹板的立模标高,上吊调整时提高了第节段的高程,造成波形钢腹板出现上挠。由工况四可以看出,移动挂篮造成的下挠值与理论计算值吻合。由工况五可知,浇筑下一节段混凝土与本节段顶板混凝土,造成的波形钢腹板局部变形值与理论计算值差别较大,且实测值均大于理论值,应考虑混凝土浇筑期施工荷载,由于泵送管泵送混凝土造成的冲击作用所导致。
4 结论
1) 悬臂长度较小时,波形钢腹板的局部变形值也较小;悬臂长度较大时,波形钢腹板局部变形值变化迅速。结果表明:主要来自混凝土浇筑和预应力张拉2个施工步骤。
2) 实际测量值与理论值存在差异,根据已有的研究可知,误差可能来源:混凝土容重实际值与理论值存在差异、温度变化引起的变形、施工活载造成的下挠等。由于本桥上下游高程不同,断面受到强烈的尾流干扰和遮挡效应,桥梁气动干扰效应对桥梁两侧断面位移也不容忽视。
3) 小悬臂节段时,波形钢腹板因受到桥墩的约束,其变形值较小。随着施工地进行,悬臂长度地增加,波形钢腹板实测局部变形值与理论值的误差迅速增加。最大悬臂状态时,计算值与实测值的误差可达到实测值的23.7%。
4) 根据实测值和计算值拟合修正公式,此公式经验证,符合后续施工阶段挠度的计算。对施工中的波形钢腹板局部变形值进行修正,可为后续施工解决腹板局部变形过大的问题,保证成桥线形达到设计要求。
[1] 王卫,张建东,段鸿杰,等.国外波形钢腹板组合桥梁的发展与现状[J].现代交通技术,2011,8(6):31−33,52. (WANG Wei, ZHANG Jian-dong, DUAN Hong-jie, et al. Development and status of composite structure bridge with corrugated steel webs on board[J]. Modern Transportation Technology, 2011, 8(6): 31−33, 52. (in Chinese))
[2] 庄艳伟,杨彪,程永志.波形钢腹板连续刚构梁桥施工技术[J].筑路机械与施工机械化,2020,37(Z1):87−90. (ZHUANG Yan-wei, YANG Biao, CHENG Yong-zhi. Construction technology of continuous rigid frame beam bridge with corrugated steel webs[J]. Road Machinery & Construction Mechanization, 2020, 37(Z1): 87−90. (in Chinese))
[3] 秦明星.波形钢腹板PC梁施工期位移分析与控制[J]. 中外公路,2017,37(3):138−140.(QIN Ming-xing.The analysis and control of displacement during construction period of PC beam with waveform steel web[J]. Journal of China & Foreign Highway, 2017, 37(3): 138−140. (in Chinese))
[4] 杨莹.大跨径预应力混凝土连续刚构桥长期下挠因素影响分析[D].西安:长安大学,2019.(YANG Ying. Analysis of long term deflection factors of long-span prestressed concrete continuous rigid frame bridge[D]. Xi’an: Changan University,2019.(in Chinese))
[5] 郑尚敏,杨丙文,万水.波形钢腹板PC组合梁桥施工阶段挠度有限元分析[C]//第20届全国结构工程学术会议论文集.宁波,2011:299−303.ZHENG Shang-min,YANG Bing-wen, WAN Shui. Finite element analysis on deformation of corrugated steel webs composite bridge in construction stage[C]// Proceedings of the 20th Ational Conference on Strauctural Engineering. Ningbo, 2011: 299−303.
[6] 邓文琴,刘朵,冯杰,等.波形钢腹板箱梁桥异步施工节段足尺模型试验研究[J].桥梁建设,2019,49(1):53−58. (DENG Wen-qin,LIU Duo,FENG Jie,et al.Segmental full-scale model test for asynchronous construction of box girder bridge with corrugated steel webs[J].Bridge Construction,2019,49(1):53−58.(in Chinese))
[7] 岳宏智,牛传同,曹洪亮,等.波形钢腹板PC组合箱梁桥异步施工全过程分析[J].公路,2020,65(5):129−134. (YUE Hong-zhi,NIU Chuan-tong,CAO Hong-liang,et al. The analysis of asynchronous construction process of prestressed concrete composite box girders with corrugated Steel webs of bridge[J].Highway,2020,65(5): 129−134.(in Chinese))
[8] 易征.连续刚构桥梁气动干扰效应数值模拟[J].交通科学与工程, 2018, 34(3): 20−26. (YI Zheng. Numerical simulation of aerodynamic interference effect of continuous rigid frame bridge[J]. Journal of Transport Science and Engineering,2018,34(3):20−26.(in Chinese))
[9] 中华人民共和国交通运输部.中华人民共和国交通行业标准:组合结构桥梁用波形钢腹板 JT/T 784—2010[S]. 北京:人民交通出版社,2010.(Ministry of Transport of the People’s Republic of China. Highway & Transportation Standard of the People’s Republic of China: Corrugated steel webs in composite structure bridges. JT/T784—2010[S]. Beijing: China Communications Press,2010.(in Chinese))
[10] Man Z,Lin A.Full-range shear behavior of a nonprismatic beam with steel trapezoidal corrugated webs: Experimental tests and FE modeling[J].Journal of Structural Engineering, 2020, 146(8):4020162.
[11] 彭官友.桥梁施工监控的改进GM(1,1)灰色预测模型研究[J]. 交通科学与工程, 2019, 35(1): 54−60. (PENG Guan-you. Application of improved GM(1,1) grey prediction model in the bridge construction monitoring[J]. Journal of Transport Science and Engineering,2019,35(1): 54−60.(in Chinese))
Study on local deformation of corrugated steel web in asynchronous suspension construction
PENG Dong-lin, YANG Jian-rong, ZHENG Xiao-long
(Construction Engineering College, Kunming University of Science and Technology, Kunming 650500, China)
To accurately calculate the local deformation of corrugated steel web in asynchronous suspension construction, the plate and shell element model was established by finite element software Midas/FEA to study the local deformation of corrugated steel web under load. The error variation between the calculated value and the measured value was analyzed. The results show that the local deformation of corrugated steel web in asynchronous construction mainly comes from the influence of load. According to the law of error change, the deflection relation is fitted out, and the local deformation value of corrugated steel web in construction is corrected to ensure that the bridge alignment meets the design requirements.
corrugated steel web; cantilever construction; continuous rigid frame bridge; asynchronous construction; local deformation
U445.4
A
1674 − 599X(2021)01 − 0089 − 06
2020−09−11
国家重点研发计划(2017YFE0103000);云南省科技富民强县计划(2015EA002);云南省交通运输厅科技项目(云交科2016(A)02)
彭东林(1993−),男,昆明理工大学硕士生。

