非等桩径荤素桩组合咬合桩受力计算模型研究

洪源，彭正坤，任晨灏，曾习凡，梅东，李繁

非等桩径荤素桩组合咬合桩受力计算模型研究

洪源1，彭正坤1，任晨灏1，曾习凡1，梅东1，李繁2

(1. 中国水利水电第八工程局有限公司，湖南 长沙 410004；2. 中南大学 土木工程学院，湖南 长沙 410075)

针对咬合桩等效成地下连续墙的理论计算模型中的不足，本研究考虑钻孔咬合桩中荤素桩之间桩径相对大小的影响及素混凝土桩的刚度折减效应，推导出修正后的等效刚度的咬合桩受力与形变理论计算模型。依托深圳市城市轨道交通12号线太子湾站主体围护结构咬合桩工程，采用Midas/GTS NX有限元软件建立了数值模拟，分析了基坑开挖全过程围护结构的受力机理与变形规律，验证理论计算模型。研究结果表明：随着基坑开挖，围护结构最大水平位移最终收敛于10 mm左右。开挖工况下，围护结构的内力与变形增长较快，尤其第三层土开挖完成后结构内力迅速增长。验证了该理论模型能够有效预测基坑施工过程中钻孔咬合桩的内力与位移发展规律，可为围护结构的合理设计与安全施工提供理论指导。

钻孔咬合桩；等效刚度法；数值模拟；受力机理；变形规律

钻孔咬合桩基坑围护结构主要包括素混凝土桩与钢筋混凝土桩，与排桩等复合桩基的不同处是咬合桩中的荤素桩相互咬合，在土体中形成了致密的止水帷幕，同时具有良好的围护性能[1−2]。钻孔咬合桩结构从空间形态上比较接近地下连续墙的形式。因此，在受力特点上，类似地连墙的受力模 式[3−4]。

目前，国内外研究学者多采用等效刚度的分析理论对咬合桩支护结构进行受力机理分析[5−7]。任红林[8]等人采用等效刚度法对钻孔咬合桩结构进行内力求解及配筋设计，证明了该方法可以满足咬合桩设计要求。廖中林[9]等人将钻孔咬合桩简化成相应厚度的地连墙，再进行咬合桩的设计与验算分析。张前[10]等人根据抗弯等效刚度原则并结合工程实例，分析咬合桩的变形与稳定时采取等效地下连续墙的力学模式。张桢[11]运用有限元数值模拟的手段，建立了钻孔咬合桩等效刚度法的有限元模型，并与实测数据进行对比，验证了模型的有效性。闫文进[12]以直线型咬合桩的等效刚度分析方法为基础，调整荤素桩的咬合角度，将其设计为折线形咬合桩结构，结合理论计算法与数值模拟方法，综合分析了桩体抗弯承载性能。本研究基于刚度等效原则，拟将钻孔咬合桩等效为地下连续墙的计算模型，并根据实际工程中荤素桩的桩体特征差异对现有的等效地连墙的计算模型进行参数修正，建立适应抛填石层超深基坑钻孔咬合桩的结构受力变形分析模型，并结合数值模拟[13−14]的方法，验证其合理性。

1 咬合桩结构理论计算模型

不同桩径的荤素桩组成的钻孔咬合桩结构计算模型如图1所示，其修正后的等效刚度的计算公式为：

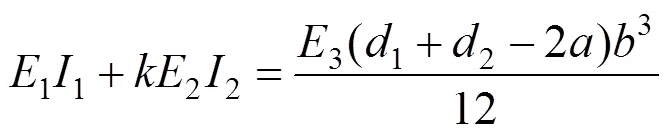
式中：I1为钢筋混凝土桩的截面惯性矩；I2为素混凝土桩的有效截面惯性矩；E1为钢筋混凝土桩的混凝土弹性模量；E2为素桩的混凝土弹性模量；E3为等效地连墙的混凝土弹性模量；d1为钢筋混凝土桩的桩径；d2为素桩的桩径；a为桩体咬合量；b为等效的地下连续墙厚度；k为素桩的刚度折减系数，参考文献[8]的折减系数取值范围，考虑该工程实际取0.8。

钢筋混凝土桩桩体截面惯性矩为：

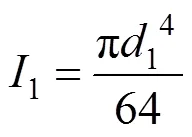
素混凝土桩的有效截面惯性矩为：

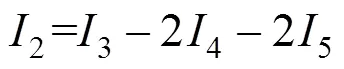
3、4及5的计算简图如图2所示，计算式为：

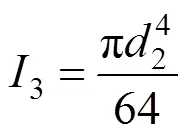
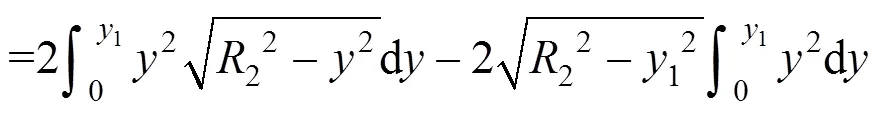
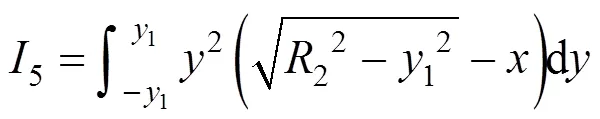
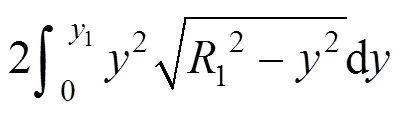
式中：3为素混凝土桩的圆形截面惯性矩；4为素混凝土桩截面弓形部分的截面惯性矩；5为钢筋混凝土桩截面弓形部分的截面惯性矩；为截面上任意点的横坐标；为截面上任意点的纵坐标；1为咬合截面高度的一半；1为钢筋混凝土桩的截面半径；2为素混凝土桩的截面半径。

将公式(4)～(6)代入公式(3)，可得到素桩有效截面惯性矩：

如图3所示，咬合桩截面等效计算模型通过分析，确定钻孔咬合桩等效刚度法的计算单元长度为(1+2−2)。

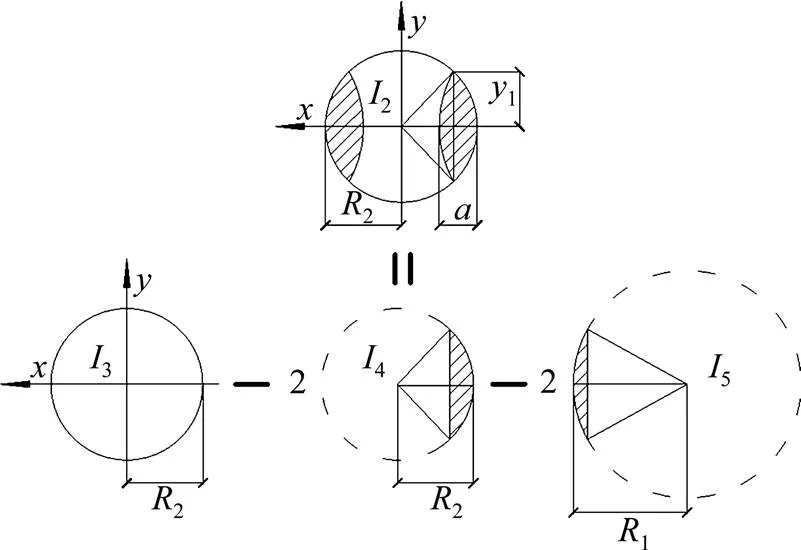
图2咬合桩截面惯性矩I2计算简图

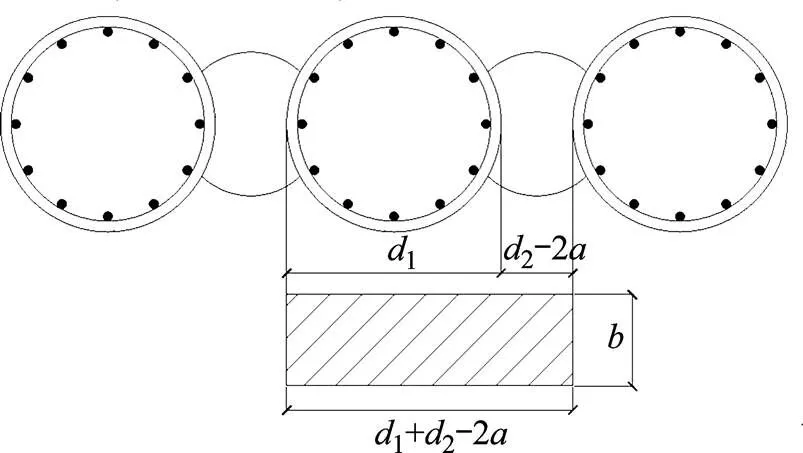
图3 咬合桩截面等效计算简图

根据式(1)，可变换成：

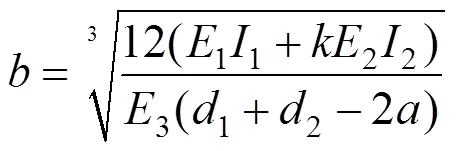
根据式(8)，可求得等效墙体的等效厚度：

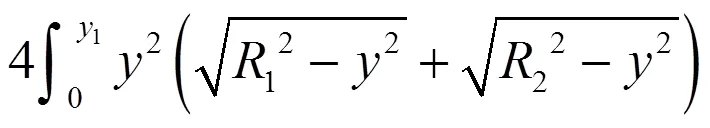
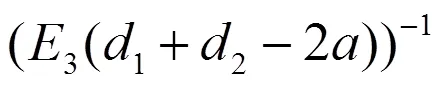
再完成等效墙体弯矩、剪力及位移的计算，并将其换算成咬合桩的弯矩、剪力及位移。换算的计算式为：

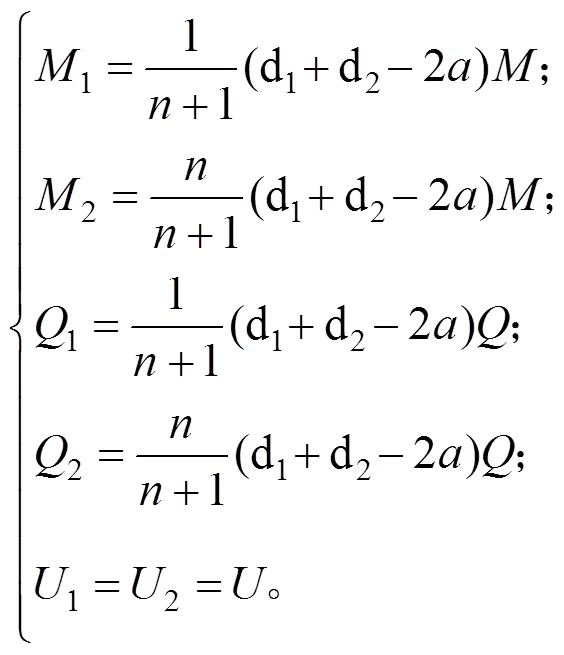
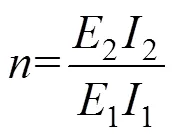
式中：为素桩与荤桩的刚度比；1为荤桩桩体的弯矩；1为荤桩桩体的剪力；1为荤桩桩体的位移；2为荤桩桩体的弯矩；2为荤桩桩体的剪力；2为荤桩桩体的位移；为等效墙体弯矩；为等效墙体剪力；为等效墙体位移。

2 咬合桩数值模拟

2.1 工程地质概况

以深圳市城市轨道交通12号线工程土建一工区太子湾站主体围护结构咬合桩工程为背景。考虑选取主体围护结构A-A横截面进行建模分析。此基坑深约30 m，宽度约26 m，场地地下水位埋深取0.88 m。自上而下分布的地层依次为：填碎石、素填土、淤泥质粉质黏土、粉质黏土、强风化片麻状混合花岗岩、中风化片麻状混合花岗岩。计算水土压力时，采取水土合算的方法，模拟区间基坑所在地层条件如图4所示。

基坑开挖分5层进行，土层厚度由上往下依次为6.9、3.1、6.3、5、5 m。基坑内竖向设5道支撑，第一、二、三、五道支撑采用800×1 000砼支撑，第四支撑采用1 000×1 200砼支撑。所有内支撑选用C30混凝土。咬合桩素混凝土桩桩径为1 200 mm，采用C20混凝土。配筋桩桩径1 500 mm，采用C35混凝土。荤桩与素桩中心距为1 000 mm，两桩的咬合量为350 mm。等效地下连续墙的有效厚度为1 250 mm，采用C30混凝土。从图4中可以看出，第一层碎填石与第二层素填土的交界线并不水平，因现场实际中碎填石层并不是均匀等厚，所以给出的地质剖面图也只能代表某一区间段的地层情况。因此，考虑到模型的准确性与简易性，本研究对于碎填石层和其他土层采取等效均匀厚度进行模拟分析。

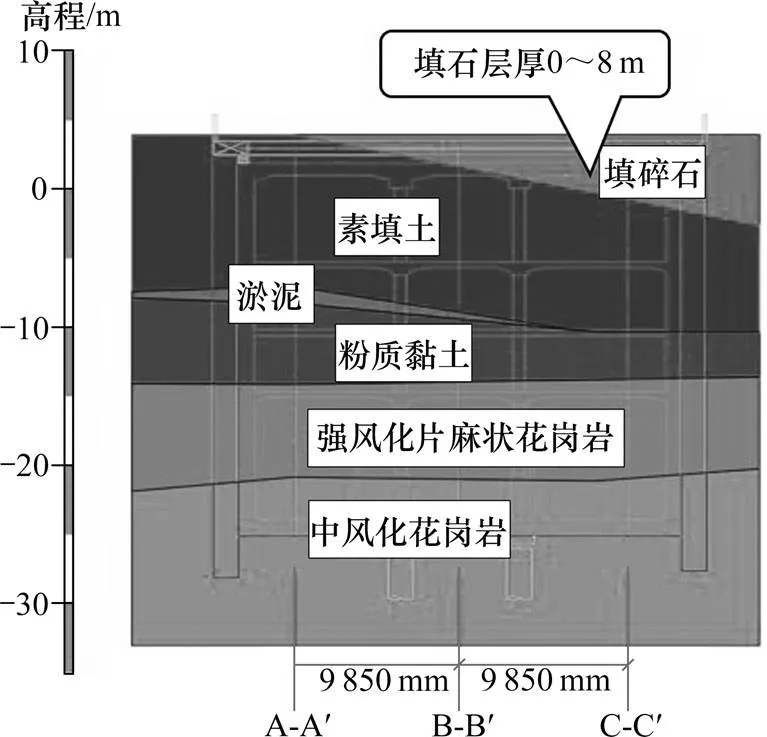
图4 模拟区间所在地层地质纵剖面

2.2 数值分析模型

采用Midas/GTS NX有限元分析软件建立围护结构模型进行数值分析。基坑竖直方向为Y轴，沿基坑水平方向为X轴，建立计算坐标系。为提高计算精度，利用混合四面体网格，在基坑内土体及围护结构施工位置处，网格划分较密；向外部土体网格划分，逐渐变疏。在不影响计算精度的前提下，减少网格数量，节省计算时间，网格单元尺寸在1.0～1.5 m，共划分6 626个单元，6 582个节点。

二维模型边界的约束为：对模型侧面垂直边界施加水平向约束，底部水平边界施加水平向约束与垂直向约束，地层表面为自由面。根据现场基坑施工的工艺流程，通过Midas/GTS NX软件，模拟围护结构施作和基坑开挖。在模型中，依据实际施工数据模拟地面施工超载及土体自重，依据相关资料的数据模拟围护结构与内支撑。其中，地面施工荷载为线压力形式，施加于基坑两侧一定范围内。其主要步骤为：

1) 初始地应力平衡。将模型内初始状态参与计算的各土层、边界条件激活，同时施加模型整体水位线，使后续计算时考虑渗流，在重力作用下达到平衡状态，并将其位移清零。

2) 围护结构施作模拟。激活该位置处的等效地下连续墙、施工荷载。

3) 基坑内土体开挖。进行该处的内支撑施作与土体开挖过程的模拟，激活该处内支撑，并钝化该处的开挖土体。

4) 待分层开挖的第一层土开挖过程计算平衡后，重复步骤三，开挖至预定的基坑底部，完成整个模型的计算。有限元数值模型如图5所示。

本模型地层及主要结构材料参数见表1。

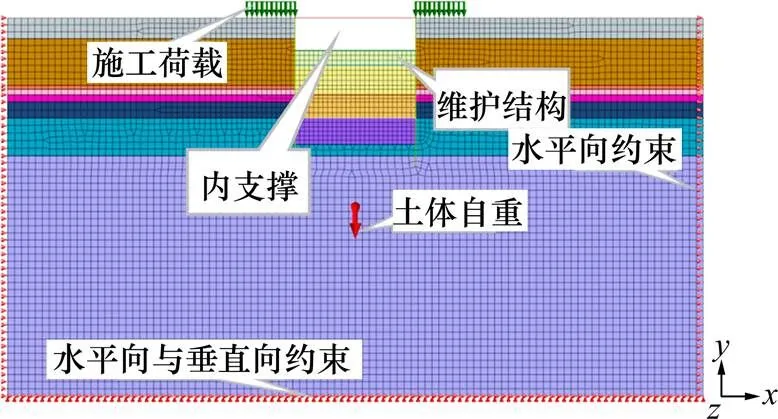
图5 围护结构数值模型示意

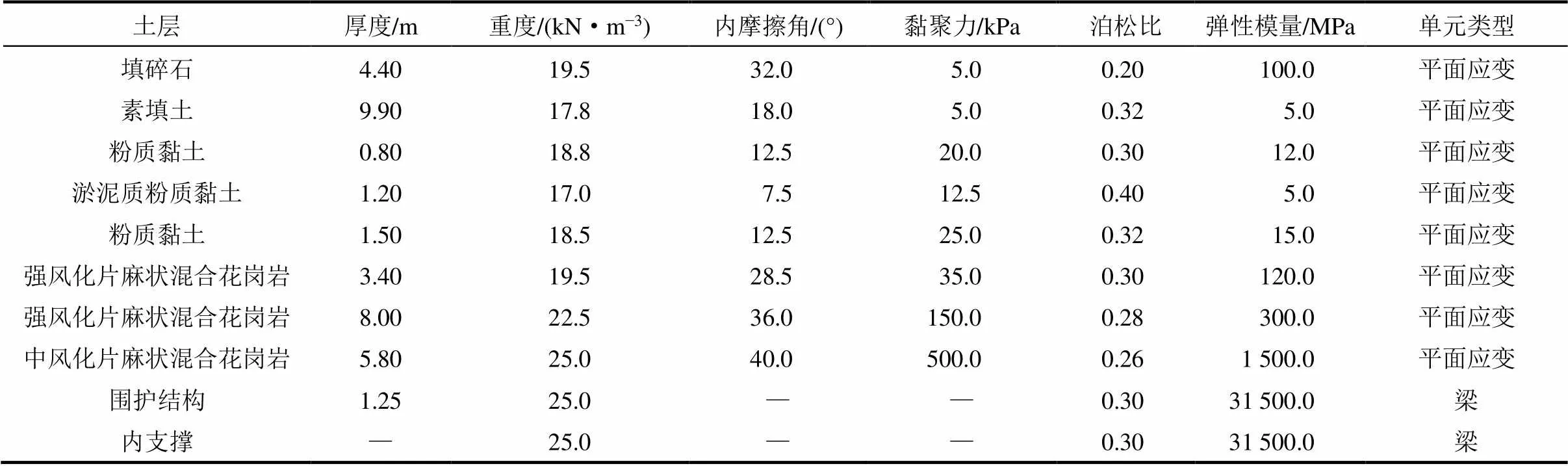
表1 模型地层参数表

2.3 理论模型与数值模型对比验证

该研究区体围护结构A-A横断面与数值模拟分析中选择的断面一致。基于不同桩径的荤素桩组成的钻孔咬合桩结构，推导出修正后的等效刚度的计算模型。将理论模型预测结果与数值模拟分析结果进行相互印证，分析两者异同，探明抛填石层超深基坑钻孔咬合桩的受力机理。在同一施工工况下，理论分析计算结果与数值模拟分析结果相互对比，给出围护结构的弯矩、剪力及水平位移变化情况，如图6～11所示。

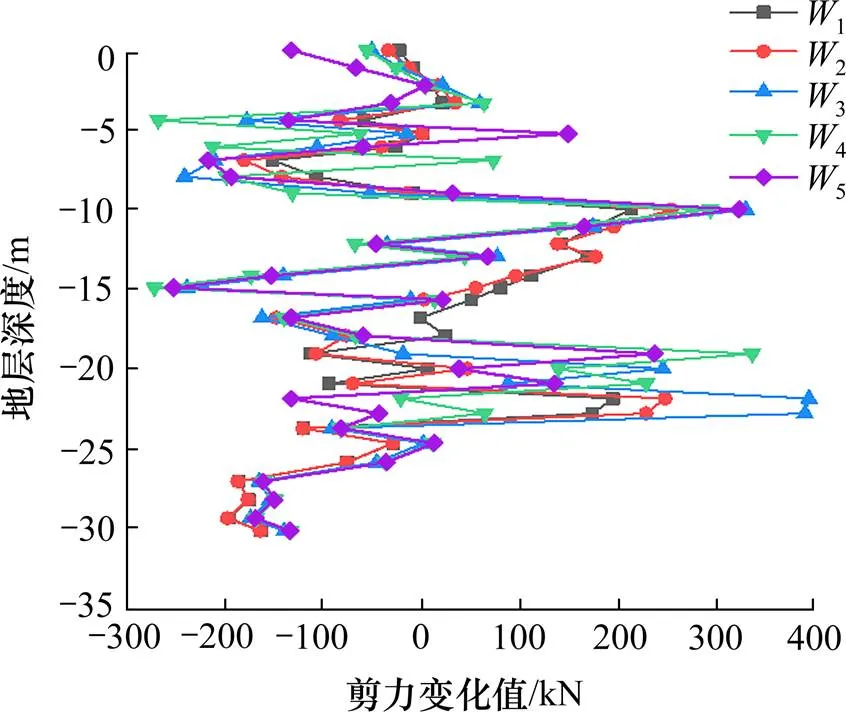
图6 各工况下围护结构剪力模拟结果

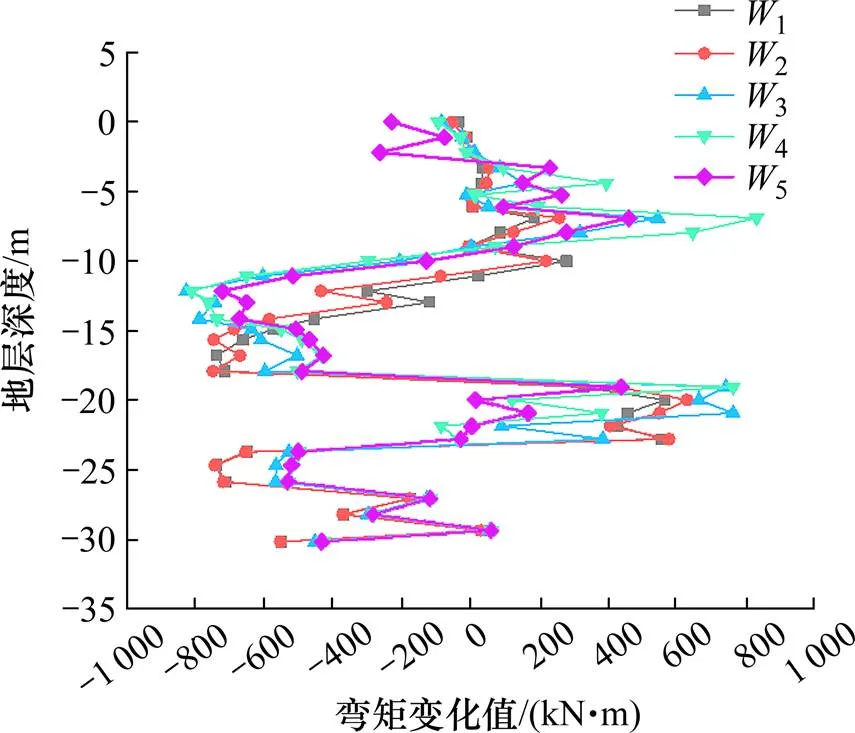
图7 各工况下围护结构弯矩模拟结果

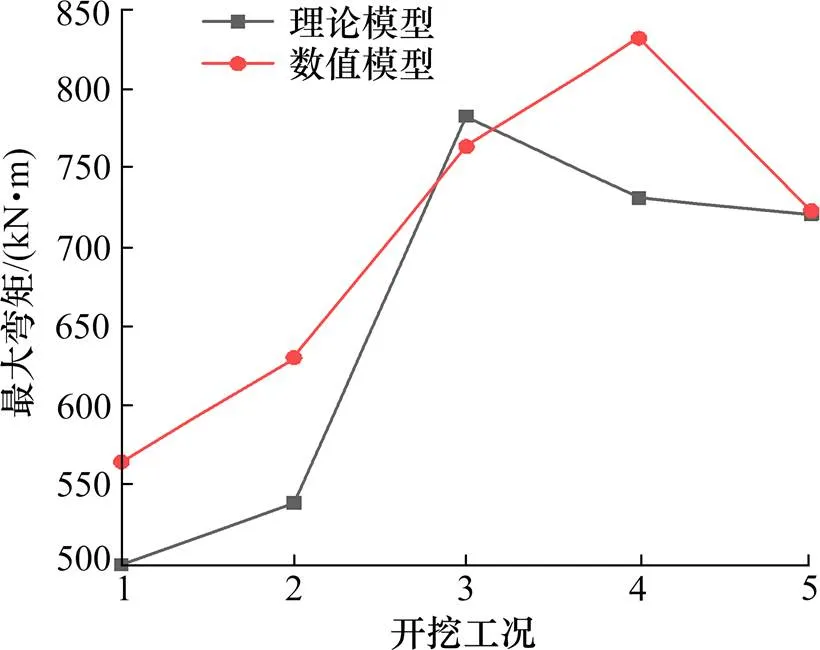
图8 理论分析与数值模拟最大弯矩对比

图6～11中的1～55种开挖工况依次代表第一层、第二层、第三层、第四层、第五层土开挖的施工工况。

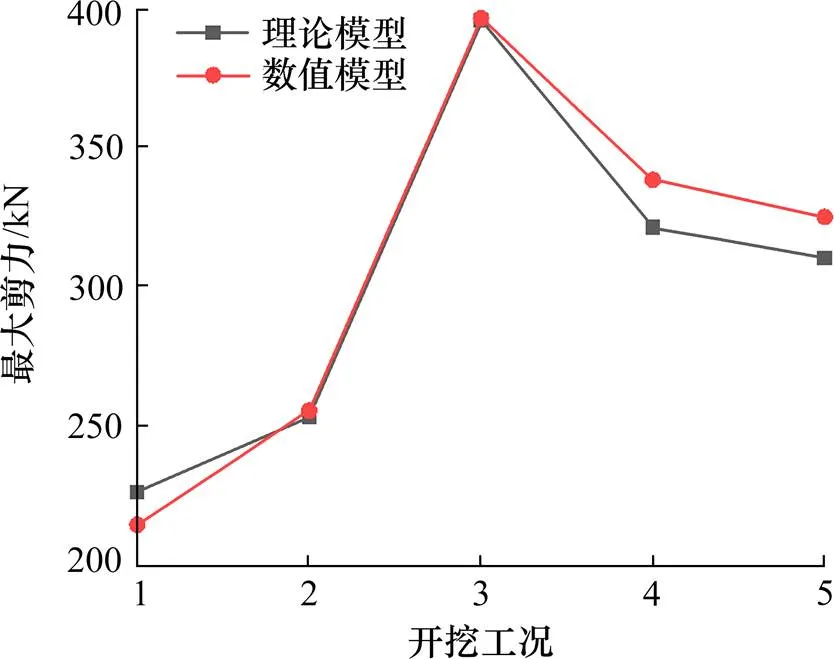
图9 理论分析与数值模拟最大剪力对比

从图6中可以看出，对应开挖工况1～5，围护结构所承受的最大剪力分别为214.234、255.177、395.866、337.91、324.601 kN，最大剪力一般发生在开挖深度16～20 m的范围内。随着开挖的进行，最大剪力的变化规律表现为先增大后降低，且剪力的增大幅度大于降低幅度。同时，围护结构在开挖完成第三层土体时，承受到最大的剪力395.866 kN。

从图7中可以看出，对应开挖工况1～5，围护结构所承受的最大弯矩分别为563.924、629.942、763.608、832.241、722.982 kN·m，最大弯矩一般发生在开挖深度18～20 m的范围内，这一变化规律与围护结构的剪力变化情况相同。最大弯矩的变化规律表现为开挖至第五层土之前持续增大，开挖完第五层土后略有降低，且降低的幅度相对较小。围护结构在开挖完成第四层土体时，承受到最大的弯矩832.241 kN·m，表明：施工到第五层土时结构所受到的弯矩最大。从每层土开挖时围护结构弯矩的增量来看，第三层土开挖完成时弯矩增量最大，为113.666 kN·m，这表明在第四层土开挖的过程中，结构的内力迅速增长。因此，为了保证围护结构的稳定性与施工安全，考虑对第四道支撑进行加强处理，如：增大其截面尺寸、增加其他预施加荷载等措施。

从图10中可以看出，对应开挖工况1～5，围护结构产生的最大水平位移分别为8.29、8.95、9.75、10、10 mm，最大水平位移发生位置分别在开挖深度8、9、11、11、11 m。随着基坑开挖的进行，围护结构的水平位移持续增大，位移最终收敛于10 mm左右。最大水平位移主要发生在11 m左右的位置，正好处于素填土的地层中，这表明该层素填土的土层性质相对较差。因此，在设计施工中，应采取相应措施进行加固。

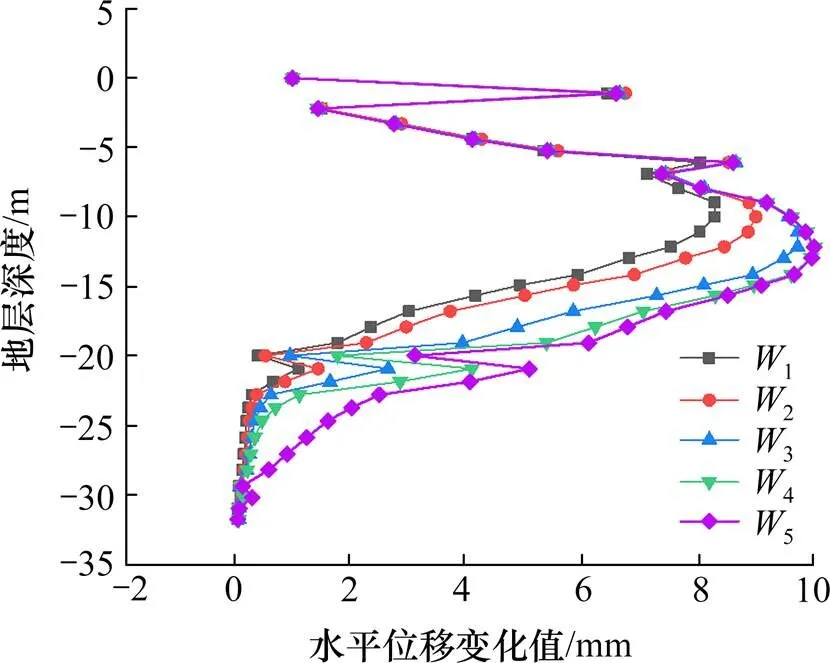
图10 各工况下围护结构水平位移模拟结果

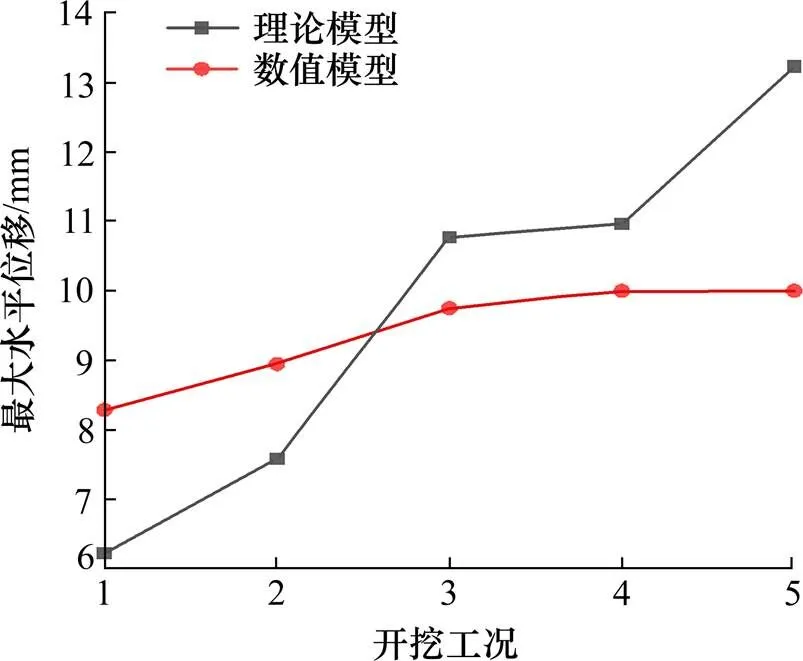
图11 理论分析与数值模拟最大水平位移对比

根据图8、图9及图11的对比情况，综合分析出基坑围护结构的内力与变形的变化趋势与数值模拟基本一致，在中间土体的开挖工况下具有良好的符合性，但在第一、二、四、五层土体的开挖工况下，呈现出一定的差异性。一方面，两者弯矩的最大偏差约为12%，剪力的最大偏差约为5%，水平位移的最大偏差约为20%，但误差均在允许范围之内，这表明预测结果与数值模拟结果相符合。另一方面，相对于数值模型，理论分析模型关于内力的计算结果偏差较小，而关于计算咬合桩在施工过程中的最大水平位移值高出一定范围，这表明采用基于不同桩径荤素桩组成的钻孔咬合桩结构，推导出修正后的等效刚度计算模型的结果是偏安全、保守的。当涉及到具体的钻孔咬合桩的设计时，可根据实际选择适应的计算方法。

3 结论与建议

基于刚度等效原则，由不同桩径荤素桩组成的钻孔咬合桩结构，推导出修正后的等效刚度的计算模型。采用Midas/GTS NX有限元软件，模拟分析了抛填石层超深基坑施工过程中围护结构的内力变化与位移演变规律，并与理论计算结果进行对比分析，得到结论为：

1) 从理论计算模型分析来看，钢筋混凝土桩与素桩承受弯矩之比约为7:3，设计过程若能合理利用素桩的承载受力性能，有利于发挥工程经济性，降低施工成本。

2) 随着基坑开挖的进行，围护结构的水平位移持续增大，最大水平位移保持10～13 mm的范围，一般发生在埋深11 m处素填土的地层中。因此，在设计施工中，应对该层土进行土体加固，可以采取预注浆加固等施工措施。

3) 在基坑开挖过程中，开挖工况下围护结构的内力与变形增长较快，及时增加内支撑，有利于降低围护结构水平位移，防止内力变形过大，出现不稳定性。

4) 从理论模型分析结果来看，第三层土开挖完成后，结构内力迅速增长，有必要对这一阶段的内支撑进行加强处理，可以适当增大第四道内支撑截面尺寸，增加预施加轴力，改善内撑混凝土强度。

5) 本研究理论模型结果是偏安全、保守的，但分析围护结构的内力与变形的变化趋势与数值模拟一致，相互印证后较符合，能够有效预测钻孔咬合桩内力与位移的发展规律，进而指导围护结构的合理设计与安全施工。

[1] Cervia A R D. Construction of the deep cut-off at the walter F. George dam[C]//GeoSupport Conference 2004. Orlando, Florida, USA. Reston, VA, USA: American Society of Civil Engineers, 2004: 530−544.

[2] Anderson T C. Secant piles support access shafts for tunnel crossing in difficult geologic conditions[C]// GeoSupport Conference 2004. Orlando, Florida, USA. Reston, VA, USA: American Society of Civil Engineers, 2004: 299−308.

[3] Finno R J, Bryson L S. Response of building adjacent to stiff excavation support system in soft clay[J]. Journal of Performance of Constructed Facilities,2002,16(1):10−20.

[4] 陈海兵,梁发云,何招智.咬合桩在邻近高填土基坑中的工程应用与实测分析[J].土木建筑与环境工程,2014, 36(3): 1−5. (CHEN Hai-bing, LIANG Fa-yun, HE Zhao-zhi. Application of secant piles in excavation pit adjacent to the high-filling surcharge loads and in situ measurements[J]. Journal of Civil, Architectural & Environmental Engineering,2014,36(3):1−5.(in Chinese))

[5] 胡琦,陈彧,柯瀚,等.深基坑工程中的咬合桩受力变形分析[J].岩土力学,2008,29(8):2144−2148,2176.(HU Qi, CHEN Yu, KE Han, et al. Analysis of bearing and deforming behavior of secant piles of deep foundation pit excavation[J]. Rock and Soil Mechanics, 2008, 29(8): 2144−2148,2176.(in Chinese))

[6] 杨虹卫,杨新伟.钻孔咬合桩的配筋计算方法[J].地下空间与工程学报, 2008, 4(3): 402−405, 414. (YANG Hong-wei, YANG Xin-wei. Computational method of reinforcement of the borehole cast-in-place pile[J]. Chinese Journal of Underground Space and Engineering, 2008,4(3):402−405,414.(in Chinese))

[7] 廖少明,周学领,宋博,等.咬合桩支护结构的抗弯承载特性研究[J].岩土工程学报,2008,30(1):72−78.(LIAO Shao-ming, ZHOU Xue-ling, SONG Bo, et al. Study on the bending performance of secant pile retaining wall[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(1):72−78.(in Chinese))

[8] 任红林,吴建忠,朱正谊.钻孔咬合桩基坑围护结构设计计算方法探讨[J].城市轨道交通研究,2010,13(9):29−32, 37.(REN Hong-lin, WU Jian-zhong, ZHU Zheng-yi. Calculation method of secant pile as excavation retaining structure[J].Urban Mass Transit,2010,13(9):29−32,37.(in Chinese))

[9] 廖中林,徐传鹏.地铁车站基坑钻孔咬合桩施工与设计[J].交通科技与经济,2013,15(2):24−27.(LIAO Zhong-lin, XU Chuan-peng. Design and construction of borehole cast-in-place piles in the subway station pit[J]. Technology & Economy in Areas of Communications, 2013,15(2):24−27.(in Chinese))

[10] 张前,杨霜,杨振甲.咬合桩等效刚度法在基坑工程中应用[J].低温建筑技术,2015,37(8):140−141.(ZHANG Qian, YANG Shuang, YANG Zhen-jia. The application of the equivalent stiffness method of occlusal piles on foundation pit engineering[J]. Low Temperature Architecture Technology, 2015, 37(8): 140−141. (in Chinese))

[11] 张桢.兰州地铁钻孔咬合桩设计优化研究[D].兰州:兰州大学,2016.(ZHANG Zhen.Design optimization of the secant pile wall at Lanzhou subway[D].Lanzhou: Lanzhou University,2016.(in Chinese))

[12] 闫文进.折线型咬合桩围护结构承载特性分析及应用研究[D].兰州:兰州理工大学,2018.(YAN Wen-jin. Analysis for the bearing characteristics and application of folded linear secant pile[D].Lanzhou:Lanzhou University of Technology,2018.(in Chinese))

[13] 张健,周中,邢凯.盾构隧道近接施工对地层变形的影响[J].交通科学与工程,2019,35(4):63−70.(ZHANG Jian, ZHOU Zhong, XING Kai. The influence of shield tunnel construction adjacent to the existing structure on deep soil displacement[J].Journal of Transport Science and Engineering,2019,35(4):63−70.(in Chinese))

[14] 周广友,李聪,胡勇,等.箱涵顶进施工过程中路面沉降的数值模拟分析[J].公路工程,2020,45(3):29−37.(ZHOU Guang-you, LI Cong, HU Yong, et al. Numerical simulation analysis of pavement settlement during the construction process of box culvert-jacking[J]. Highway Engineering,2020,45(3):29−37.(in Chinese))

Research on the force calculation model of the bored occluding pile composed of unequal diameter reinforced concrete piles and plain piles

HONG Yuan1, PENG Zheng-kun1, REN Chen-hao1, ZENG Xi-fan1, MEI Dong1, LI Fan2

(1. The Eighth Sinohydro Bureau Co., Ltd., Changsha 410004, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)

Aiming at the shortcomings in the current theoretical calculation model of occluding piles equivalent to underground continuous walls, this paper considered the influence of the relative size of the pile diameter between the reinforced concrete piles and the plain concrete piles in the bored occluding piles and the stiffness reduction effect of the plain concrete piles. The corrected equivalent rigidity occluding pile force and deformation theoretical calculation model was derived. At the same time, relying on the occluding pile project of the main enclosure structure of the Taiziwan Station of Shenzhen Urban Rail Transit Line 12, the finite element software (Midas/GTS NX) was used to establish a numerical simulation test to analyze the force mechanism and the deformation law of the enclosure structure during the whole process of excavation of the foundation pit. The deformation law verifies the accuracy of the theoretical calculation model. The analysis results of the theoretical model and the numerical model were combined to point out the structural weaknesses in the bored occluding pile engineering example, and suitable measures were given. The research results show that with the excavation of the foundation pit, the maximum horizontal displacement of the enclosure structure finally converges to about 10 mm. Under the excavation conditions, the internal force and deformation of the enclosure structure increase rapidly, especially after the third layer of soil is excavated. The theoretical model in this paper can effectively predict the internal force and displacement development law of the bored occluding pile during the construction of the foundation pit, and then guide the rational design and safe construction of the enclosure structure.

bored occluding pile; equivalent stiffness method; numerical simulation; stress mechanism; deformation law

TU753.3

A

1674 − 599X(2021)01 − 0075 − 07

2020−08−22

国家自然科学基金资助项目(50908234)；湖南省自然科学基金项目(2020JJ4743)

洪源(1991−)，男，中国水利水电第八工程局有限公司工程师。