圆弧形挡土墙整体土压力计算
方鹏,陈文胜,蒋茂林,戴嘉宁
圆弧形挡土墙整体土压力计算
方鹏,陈文胜,蒋茂林,戴嘉宁
(长沙理工大学 土木工程学院,长沙 410114)
针对计算挡土墙土压力时,因挡土墙转角处与长直墙的土压力不同,其转角处需用圆弧形挡土墙的土压力进行单独计算的问题。本研究提出将圆弧形挡土墙作为整体进行土压力计算的方法,基于库仑土压力理论和极限平衡理论,计算了挡土墙墙后滑动土体的破裂角,并用微积分计算沿墙身对称线上土压力的合力。同时考虑了墙背与墙后填土之间的摩擦力。研究结果表明:圆弧形挡土墙主动土压力及破裂角会随着墙土摩擦角的增大而减小。该计算方法可为挡土墙实际工程压力计算提供借鉴。
土压力;转角;圆弧形挡土墙;极限平衡;破裂角;摩擦力
库仑在1773年提出了以挡土墙墙后滑动土体整体极限平衡为条件的库仑土压力理论。朗肯在1857年提出了以微分土体极限平衡为条件的朗肯土压力理论。随后许多学者不断扩展了库仑和朗肯土压力理论的应用,至今为研究挡土墙土压力计算中的两种经典计算方法[1]。然而这些研究主要针对直线型挡土墙,并不适用圆弧形挡土墙进行土压力地计算。
传统土压力计算理论建立在挡土墙为无限长度,墙后滑动土体的滑动面为无限平面的基础上。但实际工程中,挡土墙的长度有限,如:桥梁的桥台,涵闸的闸墙、圆形水池、局部塌方区的挡墙及护岸墙等。此时,挡土墙墙后滑动土体滑动面由破裂面和滑动面组成,其形状是一个复杂的空间曲面,并不是一个无限平面,需基于土压力空间理论进行挡土墙土压力的研究,因此,许多学者采用了不同方法分析了圆弧形挡土墙土压力的分布。马崇武[2]等人假定圆弧形挡土墙在不同破裂角时同时达到极限平衡条件,建立了无黏性散体材料对圆弧形挡土墙侧压力的计算方法。原方[3−5]等人对圆弧形挡土墙的土压力进行了试验研究和理论建模,获得了其土压力的分布规律及计算方法,并运用于浅圆仓。Janssen[6−8]等人提出了填土对曲线挡土墙的非线性压力分布规律。胡乐山[9−12]等人对墙背为竖直、墙后填土为水平等情况下的圆弧形挡土墙土压力进行了计算分析,但这些研究都没有考虑到挡土墙墙背和填土之间的摩擦力,而实际工程中墙背并非光滑,而且存在摩擦力。因此,作者拟将圆弧形挡土墙作为整体,考虑挡土墙墙背和填土之间的摩擦力,基于库仑土压力理论和极限平衡理论,将圆弧形挡土墙整体土压力的计算从平面问题上升到空间问题,也考虑了长直墙与圆弧形墙墙后滑动土体体积的不同。运用微积分求出主动土压力的极值点,得到其整体主动土压力的大小,据此判断圆弧形挡土墙的稳定性。
1 圆弧形挡土墙土压力计算方法
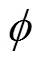
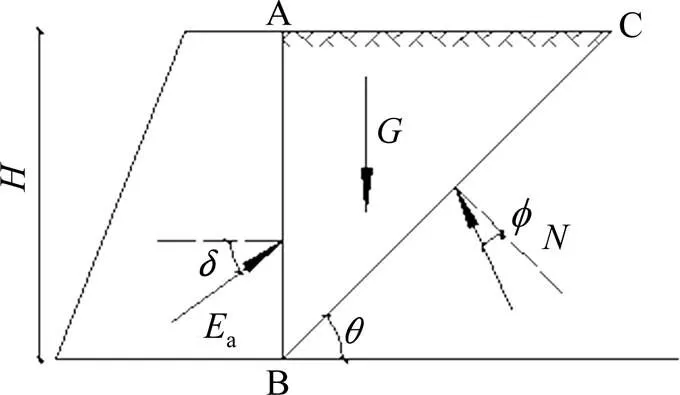
图1 圆弧形挡土墙主动土压力计算模型
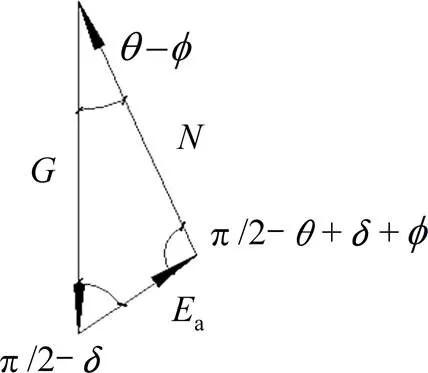
图2 力的矢量三角形
通过参考库仑土压力理论的假设和力学分析,对圆弧形挡土墙土压力进行计算。假设:①当墙体发生位移达到极限平衡状态时,将墙后土体中形成滑动面的土体视为刚体,且挡土墙各点的破裂角相等,滑动面为截圆锥面,滑动面顶部为圆环形,故滑动土体为截圆锥体,如图3所示;②将滑动土体微分化,并且每一个微分滑动土体的体积均相等;③挡土墙墙后填土为无粘性的土体;④微分土体滑动面上的摩擦力均匀分布;⑤填土表面为水平面;⑥挡土墙墙土之间存在均匀分布的摩擦力;⑦圆弧形挡土墙一般为短墙,所以这一理论适用于空间问题。
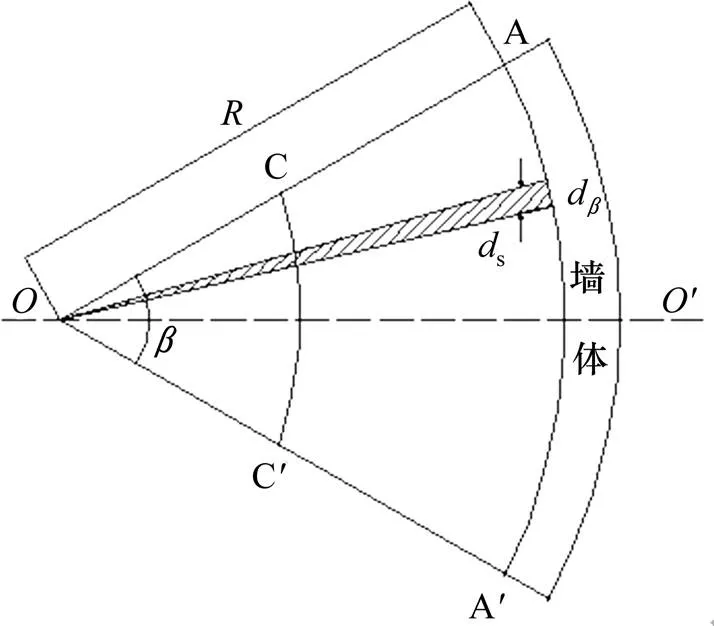
图3 圆弧形挡土墙平面示意
基于这些假定,圆弧形挡土墙所承受的主动土压力计算具有的特点:①墙后滑动土体的水平投影为扇形。在相同长度的挡土墙上,滑动土体引起主动土压力,其重力相比直墙的较小,所以主动土压力相应较小。②破裂角相比直墙的较大,则滑动土体的重力相应较小,所以主动土压力也相应较小。③圆弧形挡土墙土压力的方向沿径向分布。总主动土压力为各点土压力在墙身对称线上投影的总和,所以总土压力也相应较小。表明:可将圆弧形挡土墙作为整体,根据土压力方向的分布,计算沿墙身对称线上土压力的合力值。
2 土压力计算公式的推导
以挡土墙形式为例进行分析如图1所示。挡土墙内侧圆弧半径为,圆弧的圆心角为,填土的容重为。
由主动土压力a,滑动土体重力和滑动面上反力三力平衡的矢量三角形可得:
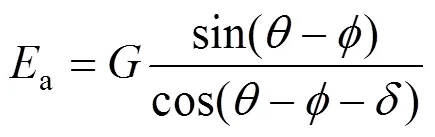
圆弧形挡土墙平面示意如图3所示,取dd为宽度计算,中心角为d的微分扇形体,则三角形ABC体积重心处的弧宽d可近似取为A、B、C三角处弧宽的平均值为:
。 (2)
则微分滑动土体的体积为:
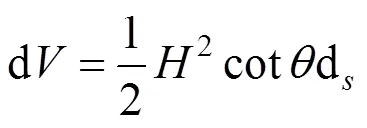
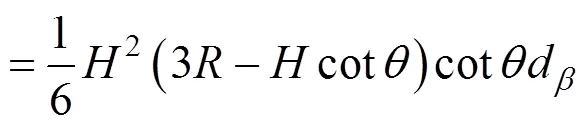
微分滑动土体的重力为:
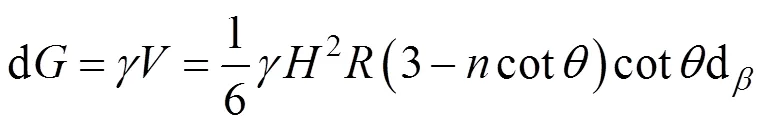
求得该微分土体所产生的土压力为:
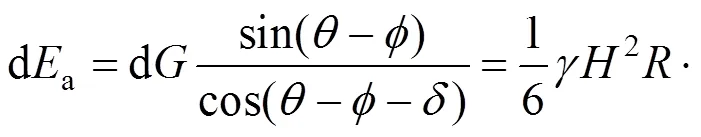
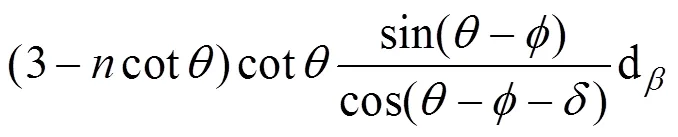
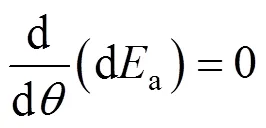
。(6)
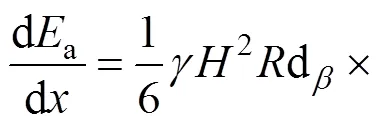
式中,=2sinicos(+);=3sinsin(+)−(cos+3sin)cos(+);=−2(cos+3sin)sin(+);=3cossin(+)。
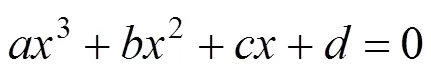
可根据卡当公式求解式(8),对其进行变量代换,令:
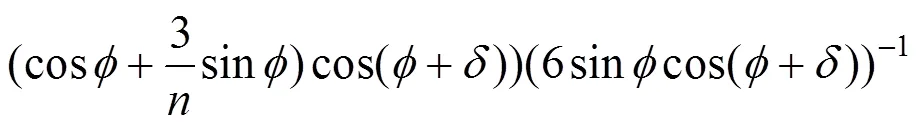
则式(9)可化为不含二次项且首项系数为1的形式,即:
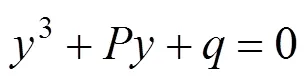
通过计算可验证得:
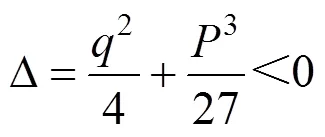
可得到求根公式:
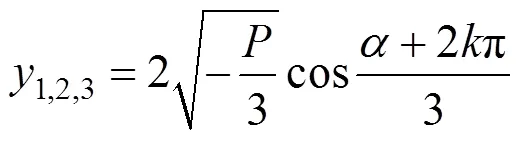
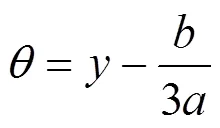

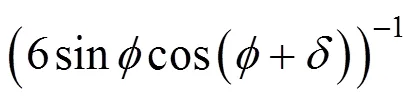
将式(13)代入式(1),便可得d宽度内承受的主动土压力。圆弧形挡土墙整体所承受的主动土压力为各点主动土压力在墙身对称线上投影的总和,通过积分得出整体主动土压力a:
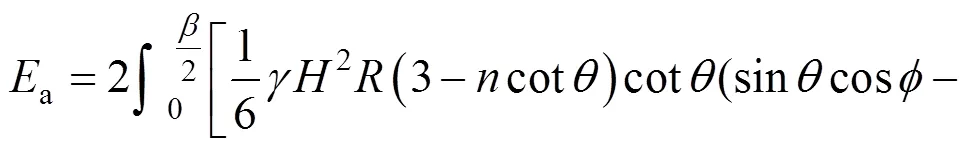
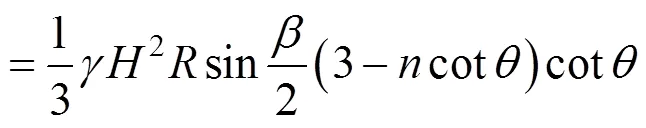
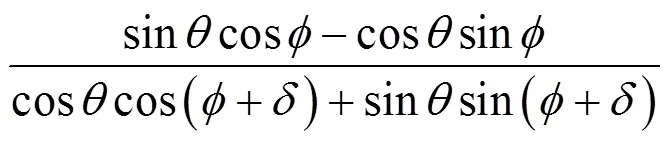
3 计算公式的优化
运用推导公式计算圆弧形挡土墙的主动土压力时会比较繁琐,而且在实践工程中应用也不方便,因此需要对推导公式进行优化。令:
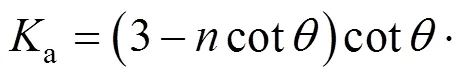
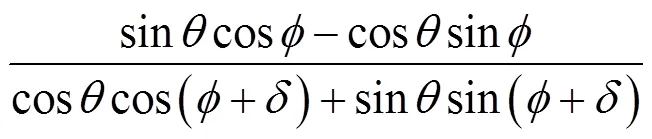
则式(14)可简化为:
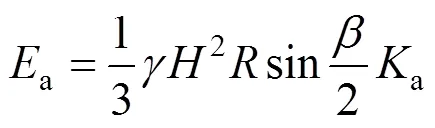
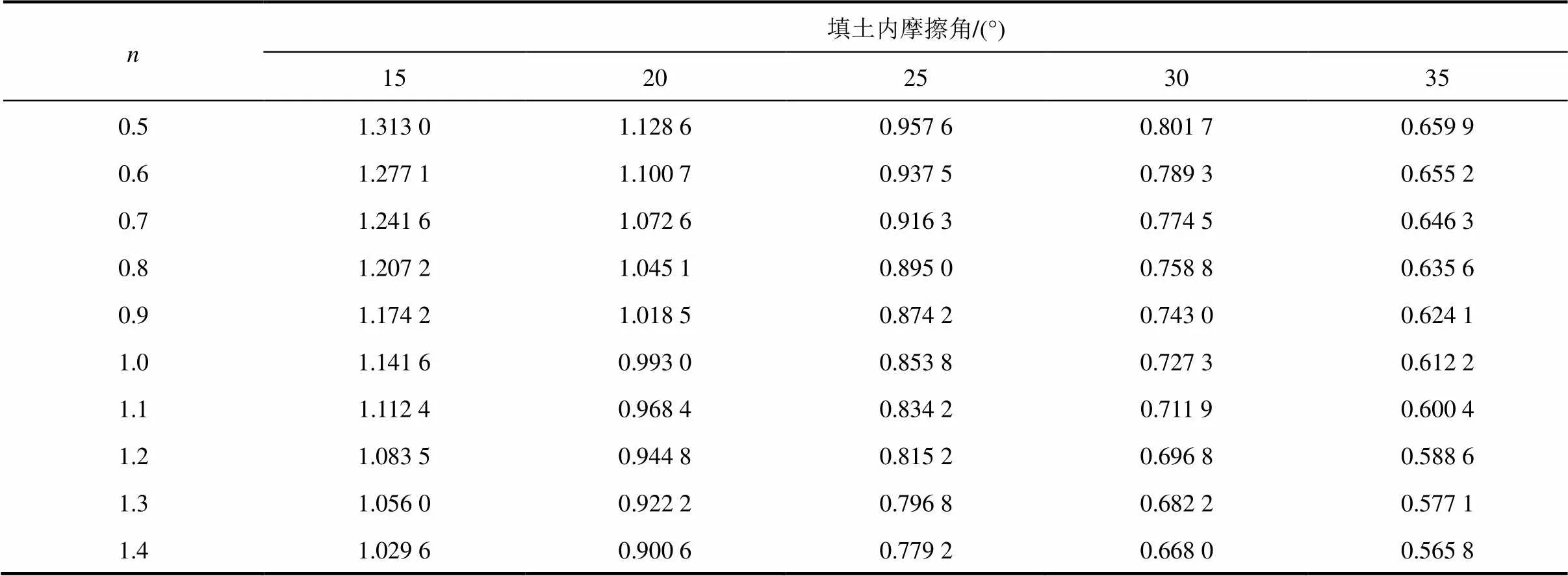
表1 Ka值(δ=15°)
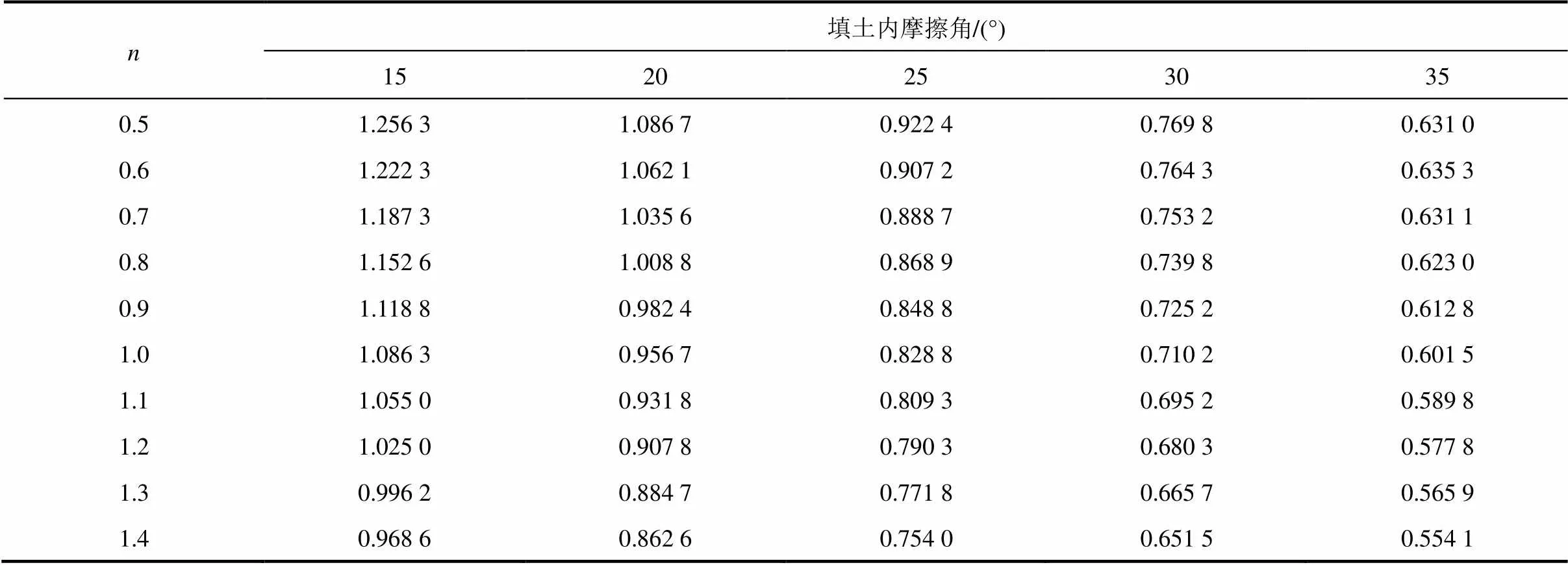
表2 Ka值(δ=20°)
4 实例分析
圆弧形挡土墙的断面图如图4所示。墙高为7.5 m,挡土墙圆心角为90°,圆弧半径为7 m,墙身为砌浆石,其容重为23 kN/m3,底板采用容重为24 kN/m3混凝土,底板与地基之间的滑动摩擦系数为0.35,墙后填土容重为18 kN/m3,土体内摩擦角25°,墙背和填土间摩擦角为15°或20°的,墙后填土容重为18 kN/m3,试求墙体所承受的总主动土压力大小,并验算其稳定性。

由图4可知=7.5 m,=7 m可得= 1.071 4。
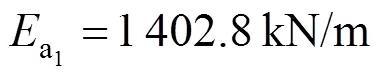
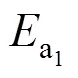
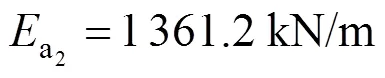
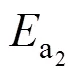
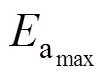
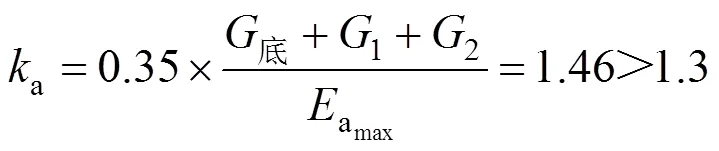
而库仑理论计算方法得到的抗滑稳定安全系数0为:
因此,利用本研究的圆弧形计算方法,会得到更为安全的稳定性系数。
5 结论
基于传统库仑理论对圆弧形挡土墙主动土压力进行计算和分析,得出的结论为:
1) 圆弧形挡土墙的主动土压力的大小和滑动面夹角度随墙土间摩擦角的增大而减小,其主动土压力强度沿墙高呈非线性分布。
2) 考虑到挡土墙墙背与墙后填土间的摩擦力,还考虑到墙后滑动土体的体积,将平面问题上升到空间问题进行研究。该计算方法适用于墙背为竖直的圆弧形挡土墙,是一种更加接近于实际情况的近似计算方法。
3) 将本研究的计算方法和基于库仑理论的计算方法进行对比,可以发现本研究计算所得的主动土压力比库仑计算法的偏小。在验证墙体的稳定性时,也比库仑计算方法更加安全。
[1] 顾慰慈.挡土墙土压力计算手册[M].北京:中国建材工业出版社, 2005. (GU Wei-ci. Manual of earth pressure calculation for the retaining wall[M]. Beijing: China Building Material Press,2005.(in Chinese))
[2] 马崇武,慕青松,蒋红英.散体材料对圆弧形外凸挡墙的主动侧压力[J].岩土力学,2010,31(3):794−798.(MA Chong-wu, MU Qing-song, JIANG Hong-ying. Granular- material-induced active lateral pressures on convex-arc walls[J]. Rock and Soil Mechanics, 2010, 31(3): 794−798. (in Chinese))
[3] 原方,王复明,肖昭然.曲线挡墙上主动散粒体压力分析及应用[J].岩石力学与工程学报,2004,23(22): 3900− 3904.(YUAN Fang,WANG Fu-ming,XIAO Zhao-ran. Analysis on active bulk-solid pressures on curvy walls and its applications[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(22):3900−3904.(in Chinese))
[4] 原方,邵兴,王录民,等.一种新的浅圆仓散料侧压力计算方法[J].工程力学,2004,21(3):96−100.(YUAN Fang, SHAO Xing, WANG Lu-min, et al. A method for calculating lateral pressures on squat silo walls[J]. Engineering Mechanics,2004,21(3):96−100.(in Chinese))
[5] 王复明,原方,师旭超.浅圆仓散料侧压力计算探讨[J]. 工程力学,2006,23(2):111−114,83.(WANG Fu-ming, YUAN Fang, SHI Xu-chao. Calculation of bulk-solid pressures in squat silos[J]. Engineering Mechanics, 2006, 23(2):111−114,83.(in Chinese))
[6] Janssen H A. Versuche über Getreidedruck in Silozellen [J]. Zeitschrift des Vereins Deutscher Ingenieure, 1895, 39(35):1045−1049.
[7] Landry J W, Grest G S, Silbert L E, et al. Confined granular packings: Structure, stress, and forces[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2003, 67(4 pt 1): 041303., 67(4Pt1): 041303/1− 041303/9.
[8] Landry J W, Grest G S. Granular packings with moving side walls[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics,2004,69(3 Pt 1):031303.
[9] 胡乐山.圆弧形挡土墙主动土压力计算[J].水利水电技术,1982,13(5):31−37.(HU Le-shan.Calculation of the active soil pressure of circular retaining wall[J]. Water Resources and Hydropower Engineering,1982,13(5):31− 37.(in Chinese))
[10] 单锦洪.圆弧形挡土墙的整体计算[J].水利水电技术, 1983,14(11):10−15.(SHAN Jin-hong.Calculation of the Active Soil Pressure of Circular Retaining Wall[J]. Water Resources and Hydropower Engineering,1983,14(11):10− 15.(in Chinese))
[11] 何俊.圆弧形挡土墙稳定计算[J].海河水利,1989(5):52− 57,64,61.(HE Jun. Stability calculation of circular retaining wall[J].Haihe Water Resources,1989(5):52− 57,64,61.(in Chinese))
[12] 黄旺, 杨建军, 黄娟. 几种挡土墙主动土压力理论对比及墙体应力分析[J]. 长沙理工大学:自然科学版, 2017, 14(3): 29−34. (HUANG Wang, YANG Jian-jun, HUANG Juan. Comparison of several active earth-pressure theories and stress analysis for retaining walls[J]. Journal of Changsha University of Science & Technology: Natural Science,2017,14(3):29−34.(in Chinese)
Calculation of integral earth pressure of circular retaining wall
FANG Peng, CHEN Wen-sheng, JIANG Mao-lin, DAI Jia-ning
(School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China)
When calculating the earth pressure of the retaining wall, it is usually considered that the earth pressure at the nook of the retaining wall is different from that of the long straight wall. The earth pressure at the nook is calculated separately with the earth pressure of the circular retaining wall. This study proposes a method for calculating the earth pressure of the circular retaining wall as a whole. Based on the Coulomb earth pressure theory, the limit equilibrium theory is used to calculate the rupture angle of the sliding soil behind the retaining wall. Then calculus is used to calculate the resultant force of the earth pressure along the symmetry line of the wall, which can consider the friction between the wall back and the backfill at the same time. The results show that the active earth pressure and the rupture angle of the circular retaining wall decrease with the increase of the friction angle of the soil wall. This calculation method can provide a reference for the earth pressure calculation of the actual retaining wall engineering.
earth pressure; nook; circular retaining wall; limit equilibrium; rupture angle; friction
TU432
A
1674 − 599X(2021)01 − 0069 − 06
2020−02−22
国家自然科学基金资助项目(51778067,51279018)
方鹏(1995−),男,长沙理工大学硕士生。

