考虑耦合网络区域特性的充电站规划方法

杨 娴，贾志坚，赵 熠

(1. 湖南城市学院 机械与电气工程学院，湖南 益阳 413000；2. 国网湖南省电力有限公司 益阳供电分公司，湖南 益阳 413000)

汽车行业的迅速发展，不仅加剧了对化石能源的大规模开采，而且还造成了严重的空气污染问题.电动汽车作为传统汽车的替代品，是推动新能源发展的中坚力量，能有效应对能源短缺和环境污染的问题，有利于社会经济健康可持续地发展[1-2].但电动汽车会受到续航里程的限制，为保证电动汽车在行驶过程中及时补给电量，对电动汽车充电站的位置和容量的合理规划，是电动汽车推广应用的前提和基础[3].

合理规划充电站的位置和容量，不仅有利于提高电动汽车用户的便利度，而且能够降低其对电网和路网等基础网络的影响，提高规划的经济性[4-7].文献[8-9]通过分析电动汽车的充电行为和充电站的规划因素，对充电站的长期建设和连续优化提出了原则性要求及相关条件.文献[10]通过研究电动汽车在高速路网中的充电站分布需求，在最优建站的定容选址中考虑了电网接入成本.文献[11]通过分析交通起止点确定充电站需求，并基于系统电压的稳定性和充电服务质量，建立充电站选址方案.文献[12]在为电动汽车推荐最优充电站及规划行驶路径等问题中，采用路段的权值法和Dijkstra 最短路径法，一定程度上解决了大规模充电行为带来的局部交通拥堵问题.文献[13]在满足充电需求的前提下，首要考虑最小化建设充电站的数量，从而减少充电站的建设和维护成本，提高了选址经济性.

关于充电站规划的评价问题，主要考虑充电站在建设期和投入使用后所花费的成本[14-15]，确定其优化目标和相关约束条件，进一步确定优选方案[16-17].文献[18]基于充电站投资收益和充电用户效用耦合决策，提出了一种电动汽车充电站双层优化模型，并通过混合变邻域粒子群算法对其求解.文献[19]分析了充电站前期投资、运行费用与充电服务范围的关系，提出了双目标函数的数学优化模型，并采用粒子群算法进行求解.文献[20]提出了一种计及充电站的成本效益及全寿命周期成本的优化规划模型，并采用量子遗传算法求解该模型.

本文基于现有的研究成果，对充电站规划问题开展研究和分析.首先，对耦合网络、充电站选址和定容问题建模，以行驶距离最小为目标函数，构建电动汽车充电站的规划模型；其次，利用道路的动态车流量和停放车辆的固定车流量共同表示路网的交通流量，基于Voronoi 图实现对路网的区域划分；最后，采用改进粒子群算法对所提出模型进行优化、求解，并通过算例分析验证所提方案的合理性和有效性.

1 网络模型

O-D(origin-destination)线路是指电动汽车用户从出发地驶往目的地所选择的路径.文中假设规划区域有10 条O-D 线路，相互交叉形成48 个路网节点，该区域路网结构示意图如图1 所示(图中数字1～48为线路交叉形成的路网节点序号).通常，电网节点和路网的交叉路口位于同一地理位置.本文将电网和路网视为一个耦合网络，基于IEEE33 节点系统构建耦合网络的结构，如图2 所示.其中，实线表示交通线路；虚线表示电力线路(图中数字0～32 为电网节点序号).根据电力线路的分支，将该耦合网络分为工业区、住宅区和商业区3 个区域.

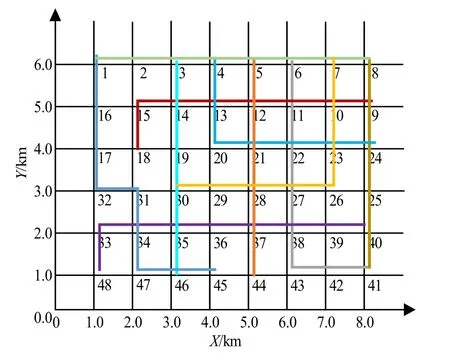
图1 规划区路网结构示意

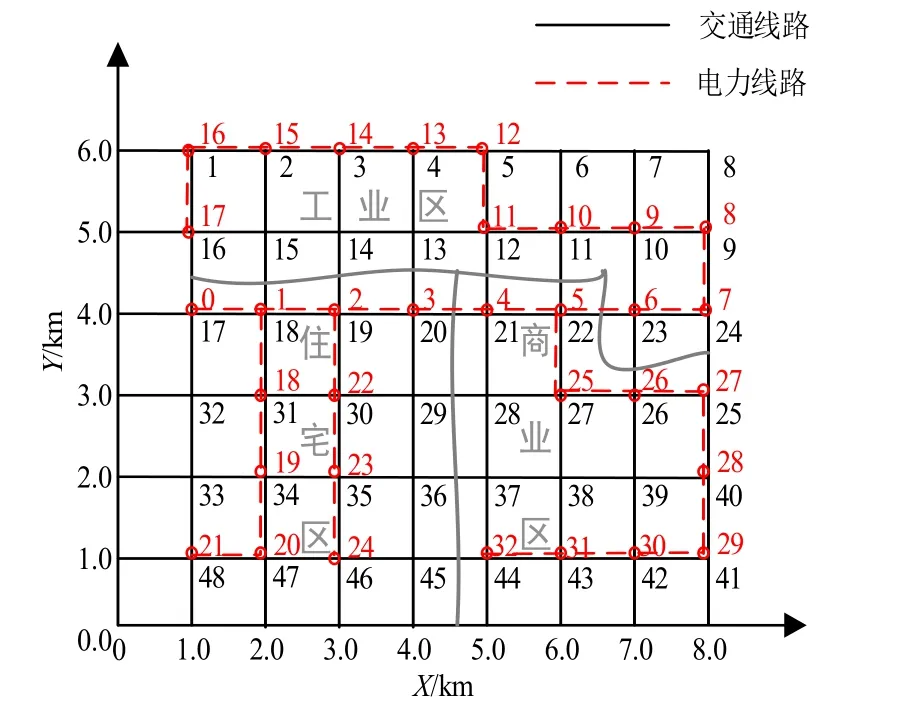
图2 耦合网络结构示意

选择合适的居民区充电站站址，主要是为电动汽车用户提供方便快捷的充电服务，而用户的充电成本主要取决于电动汽车所在位置及其与充电站的距离，其目标函数为

其中dij为节点i到节点j的几何距离.

其中，ρ为充电站容量裕度；P为充电功率；kx为充电机效率；Tv为有效充电时间；kt为充电机同时工作的比率.

2 基于Voronoi 图的定容选址模型

2.1 充电站初始化确定

在规划区范围内，充电站数量受到总充电需求和充电站容量限制的影响.规划区充电站的数量N应满足

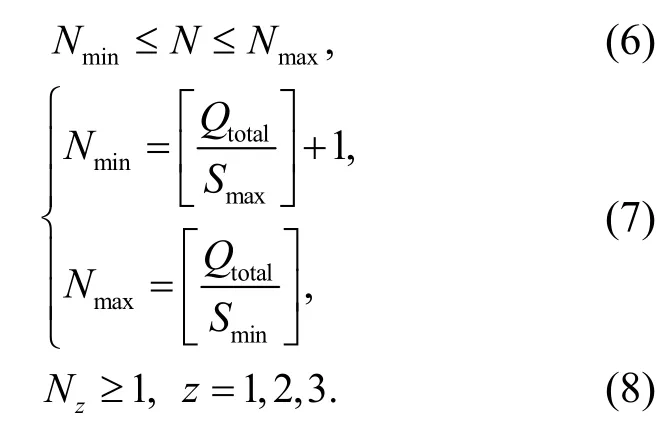
其中，Qtotal为总充电需求；Smin为充电站的最小容量限制；Smax为其最大容量极限；Nz表示所划分3 个区域的充电站数量.式(8)说明工业区、住宅区和商业区中至少有1 个充电站可供电动汽车充电.文中采用坐标几何法来表示充电站初始站址的选择，随机选取了N个节点作为充电站的初始站址.

2.2 Voronoi 图

在电力系统中，Voronoi 图主要被用于变电站的规划.Voronoi 图是以点集G中每个点为生长核，按照相同的速率向四周扩张，至相互遇到的时候，所形成的几何图形.这样，除边界上的一些点外，其余各点都可以构成凸多边形.设G为平面上的点集合，其数学定义可描述为

值得注意的是，在Voronoi 图所形成的子区域内，任意一点到该生长核的距离都小于该点到其它生长核的距离.利用这一特点，把充电站的初始站址作为生长核，则该规划区域会相应地被划分为若干个子区域，每个子区域即为初始站址的充电站所对应的服务区域.

3 模型求解

3.1 改进粒子群算法

本文提出的充电站优化规划模型是一个非线性的复杂化模型，适合采用改进的粒子群算法进行求解.在粒子群算法的基础上引入惯性权重系数ω，以控制和调整微粒的速度.例如，微粒i在空间中的速度和位置分别记为

在迭代过程中，通过比较各微粒的目标函数，跟踪每个微粒所经过的最佳位置pbest和群体所发现的最佳位置gbest，再根据式(11)～式(12)来更新各微粒的速度和位置.

其中，ωmax和ωmin分别表示ω的最大值和最小值；t表示当前迭代步数；tmax表示最大迭代步数.

3.2 总体规划流程

基于改进粒子群算法的充电站规划总流程如下(见图3)：1)如式(7)所示，根据总充电需求和充电站的容量限制预估充电站数量；2)随机选取N个节点作为充电站的初始站址；3)利用Voronoi图划分充电站的服务范围，使得服务范围内的任意位置至该充电站的几何距离最小；4)基于改进粒子群算法，根据求解所得的最佳位置更新充电站站址；5)判断是否达到最大迭代次数，若达到最大迭代次数，则输出充电站站址、覆盖路网范围和充电成本等规划方案，否则返回步骤3).

4 算例分析

基于本文所提出的充电站优化规划方法，以某区域的电动汽车充电站规划为例进行分析.其中，10 条O-D 线路的车流量如表1 所示，各路网节点的坐标及固定车流量(即该节点停靠的车辆数)如表2 所示.从表1 可以看出，途经节点1 的O-D 线路有2 条，其中1 号线路的车流量为1 488辆，2 号线路的车流量为1 240 辆；同时，节点1上的固定车流量为60 辆.假设电动汽车所占比例为15%，充电率为10%，每辆电动汽车的平均容量为50 kW·h，单台充电机功率为96 kW，充电效率为0.9，同时率为0.8～1.0(文中取0.9).充电站中充电机的数量选取要合理，若充电机数量太少，则该充电站的建立对资源利用率而言是一种浪费；若充电机数量太多，则可能对电网运行构成威胁，并容易对路网局部造成拥堵.基于此，文中设定充电站最小容量配置为6 台充电机，最大容量配置为30 台充电机；充电站有效充电时间为16 h，充电站的容量裕度为1.2.

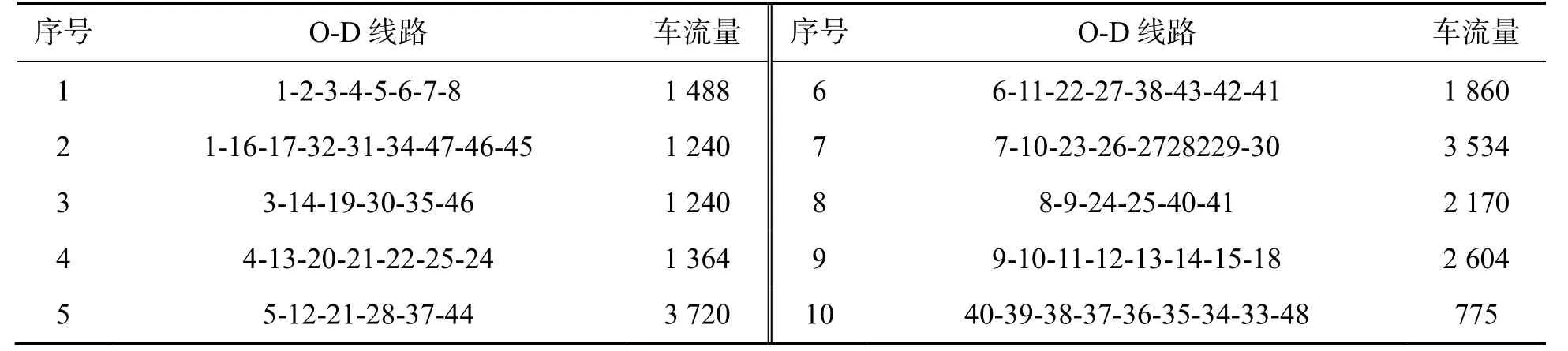
表1 O-D 线路车流量 辆

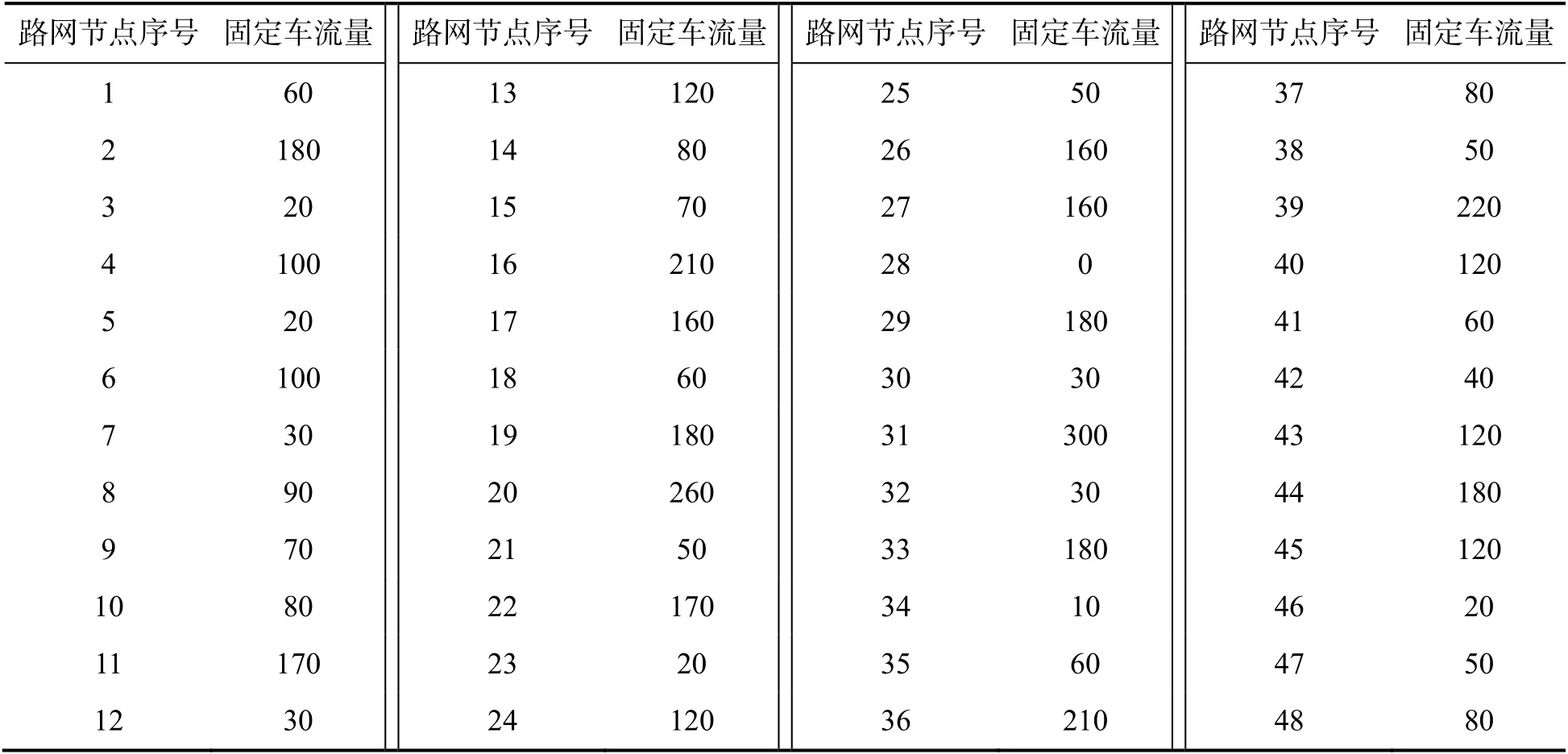
表2 各路口节点坐标及固定车流量 辆

利用式(7)预估规划区的充电站数量，范围为Nmin= 3，Nmax= 10.充电站数量与充电成本的关系如图4 所示.

图4 充电站数量与充电成本关系曲线

由图4 可知，充电站数量越多，电动汽车用户前往充电站的平均几何距离越短，所以充电成本就越低.

进一步针对充电站数量为5，7，9 进行3 种案例规划.基于改进粒子群算法，以行驶路径最短为目标，选择充电站的站址和接入位置，用Voronoi 图实现充电站服务范围的自动划分.充电站数量及位置坐标、充电机配置数、充电站所覆盖的路网节点序号及充电成本如表3 所示，充电站布局和对应的服务范围划分如图5 所示.

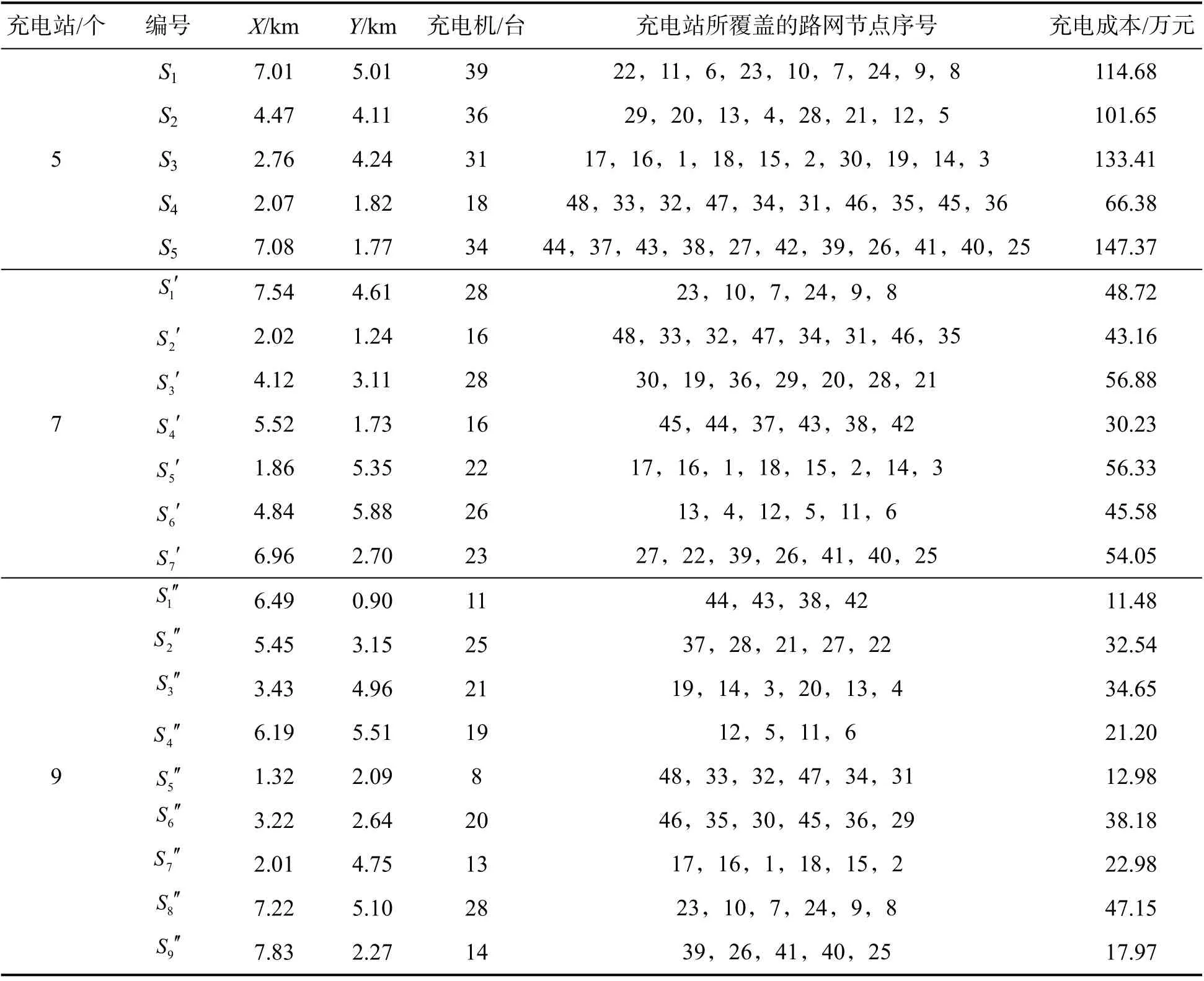
表3 不同数量充电站时的配置规划及充电成本

从表3 可知，当充电站数量为5 个时，其中4 个充电站的充电机配置数量超过最大限度(最大限度为30 台)，该充电站规划方案不可取.对1S(7.01，5.01)站址的充电站而言，需要配置39 台充电机，已超过最大配置充电机数量的限度.此时，当所有充电机同时工作时，对应节点的电网负荷将增加5 747 kW，这会对电网产生强大的冲击，影响电网的稳定运行.当充电站数量设置为9 个时，S8′(7.22，5.10)站址的充电站将配置最多的充电机(28 台)，此时，对应节点的电网负荷最多增加4 094 kW，这将大大缓解电网压力.

总的来说，充电站数量的设置要结合当前网络规模，也要符合网络规划的发展，充电站数量越多，其建设成本和运行维护成本越大.对用户而言，由于前往充电站的距离减小，充电成本相应减少；对运营商而言，单个充电站所覆盖路网节点的区域较小，其配置的充电机台数相应较少，在一定程度上可缓解充电站节点附近电网的负荷过重的压力.

图5 充电站布局及其服务范围划分

5 结论

本文综合考虑网络结构、交通流量、区域划分等耦合网络区域特性，构建了一种电动汽车充电站的优化规划模型.充电站址的选择以电动汽车用户的利益为中心，充分考虑用户出行的便捷性和经济性；以行驶距离最小化为目标函数，用Voronoi 图的“生长核”作为充电站站址，划分规划区域中各充电站对应的服务范围；结合O-D 线路的车流量和路网节点处的固定车流量，确定充电站的容量配置；基于改进的粒子群算法，通过迭代最佳位置不断更新优化充电站址.

当充电站数量分别为5，7，9 时，通过比较充电站位置和充电机容量配置可以看出，在不考虑充电站的建设成本和维护成本的前提下，充电站数量越多，越能缓解大规模电动汽车同时充电时带给电网的压力.例如，当充电站数量为5 个时，单个充电站的最大负荷可达5 747 kW；当充电站数量增加至9 个时，单个充电站的最大负荷为4 094 kW.实际算例表明，本文所提出的规划方法和模型对电动汽车充电站的站址优化具有一定的合理性和有效性.