一种电动汽车充电系统单相整流有源滤波方法

霍现旭，项添春，李树鹏，毕宇轩

（1.国网天津市电力公司电力科学研究院，天津 300384；2.天津大学电气自动化与信息工程学院，天津 300072）

近年来，随着化石燃料减少等能源危机的出现和大气污染等环境问题的加剧，使用新能源的分布式发电得到了越来越多的应用[1-3]。其中，小容量分布式电源构成的微网，由于其能源利用率高、安装方便灵活等优势获得了更多的关注[4-7]。

直流微电网结构如图1所示。在直流微电网中，电动汽车作为一种常见用户[8-9]，其充电系统的相关研究受到了广泛的关注[10]。其中单相PWM整流器由于其高效率、小体积、低成本和高可靠性的优点，在电动汽车充电系统中得到了广泛的应用[11-13]。而当直接接入交流单相电网时，电动汽车通过使用一体化充电系统，使单相整流器由电动汽车电机驱动器复用得到。但单相整流器工作时，其直流母线上产生的电压二次纹波会给充电系统带来诸多危害[14]。

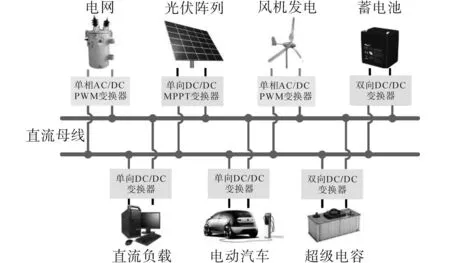
图1 直流微电网结构图Fig.1 Structure diagram of the DC microgrid

电动汽车使用单相电网给动力电池充电时，直流充电电压的二次纹波会使电池发热，降低充电效率并损害电池寿命[15]，也相应的会影响充电时电动汽车上散热风扇、空调等电机驱动系统的性能[16-18]。而在网侧，由于直流侧二次纹波经控制系统负反馈进入控制环中，网侧电流会相应产生畸变，影响网侧电能质量。由于以上问题，电动汽车充电系统中，单相PWM整流直流侧电压二次纹波抑制已逐渐成为国内外学者的研究热点。

由于无源滤波存在体积大、功率密度低等缺点[19-20]，在实际应用中一般选用有源滤波方式来抑制直流侧电压的二次纹波。文献[21-22]在传统控制方法的基础上进行了改进，避免了传统有源滤波控制方案的谐振问题。文献[8]对一种已有的有源滤波拓扑提出了新的控制方法，但这种控制方法需要在三相输入都有电感时才能够适用。文献[23]仅使用1个H桥，同时使用2个电容对称连接在交流电源两端，此时2个半桥均复用做PWM整流和有源滤波，这种方法会使得开关管的电流应力大于单相PWM整流时的电流应力。

本文提出了一种可应用于电动汽车一体化充电系统中的单相整流有源滤波方法。这种方法使用电机驱动器的三相半桥作为整流器用于单相整流。通过采用所提出的控制方法，在实现输入电流跟随电网电压正弦变化、功率因数接近于1、电流总谐波畸变率（total harmonic distortion，THD）相较不使用有源滤波可得到改善的同时，能得到稳定的直流输出电压且电压二次纹波明显减小。而通过复用2个半桥，相较于传统有源滤波拓扑，可进一步简化电路并降低充电器成本。本文首先分析了单相PWM整流的直流电压二次纹波的产生机理及有源滤波器的拓扑结构；然后就所提出的有源滤波控制方法的运行原理进行分析和推导；最后进行仿真模型的搭建，结果分析验证所提方法的正确性和有效性。

1 有源滤波拓扑推导及原理分析

1.1 单相整流直流侧电压二次纹波产生机理

传统的单相PWM整流器拓扑如图2所示。

图2 传统单相PWM整流器拓扑结构Fig.2 The rectifier topology of the traditional single-phase PWM

设电网侧交流电压us为理想的正弦波，角频率为ω，交流侧输入电流is也无畸变，则可表示为

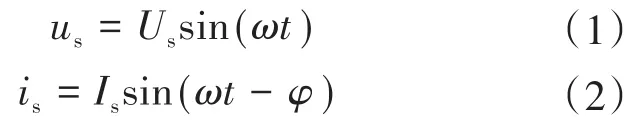
式中：Us，Is分别为电网输入电压、输入电流的幅值；φ为交流输入电压电流的相位差，即功率因数角。

由式（1）、式（2）可得交流侧的瞬时输入功率Pgrid如下式：

由式（3）可知，Pgrid可分为直流功率分量Pg1和二次脉动功率分量Pg2ω：

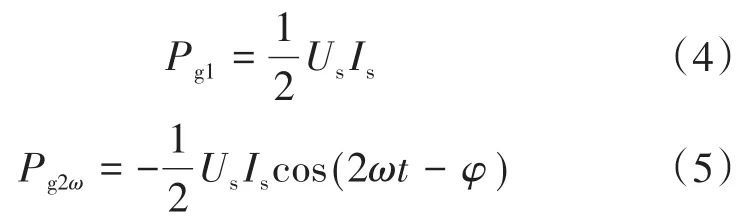
直流分量即为输入功率的有功部分；二次分量则为瞬时无功。

将开关管等同为理想开关管时，可得到功率平衡方程如下：

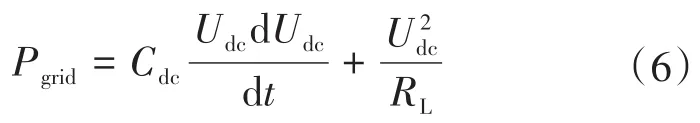
式中：RL为直流侧电阻负载。

将式（6）代入式（3），设t=0时，输入功率Pgrid的初值为P0，输出电压的初值为Udc0，可得直流侧电压Udc的表达式为

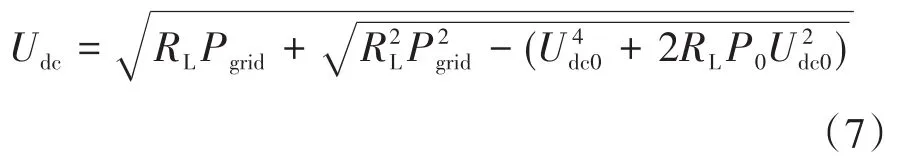
对Udc进行傅里叶分析后可知，由于二次脉动功率的存在，直流侧电压中会产生二次纹波。

为了抑制直流电压的二次纹波、降低功率损耗和提高系统的功率密度，一般采取电容储能型滤波。由于电容的容抗明显大于电路中电感的感抗，一般为计算方便忽略掉电感所吸收的二次脉动功率。此时要求滤波电容能吸收交流侧输入的二次脉动功率，即

当滤波电容功率满足式（8）时，可实现单相PWM整流直流侧电压的二次纹波抑制。

1.2 单相整流有源滤波拓扑推导

电动汽车一体化充电系统工作原理如图3所示。

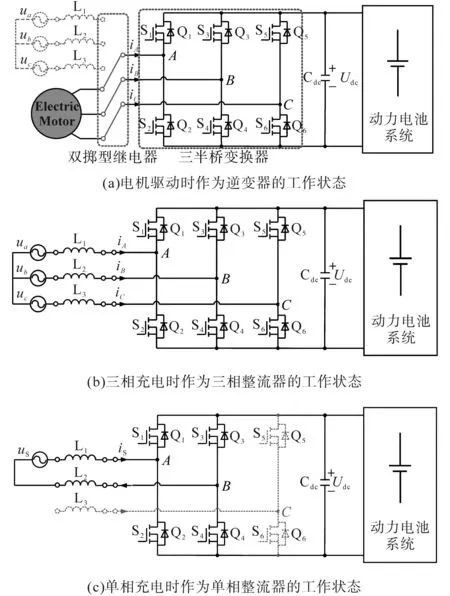
图3 电动汽车一体化充电系统工作原理Fig.3 Working principle for the integrated charging system of electric vehicles（EVs）

由图3可知，电动汽车驱动器由A，B，C 3个半桥组成，且不同模式下各半桥的工作情况各有不同。但如前文分析，在单相整流模式工作时，整流器直流侧会产生二次纹波，因而需要进一步改进单相充电时的整流器拓扑及相应控制结构。

传统的单相整流有源滤拓扑如图4所示。在传统的有源滤波电路中，A，B半桥用于单相PWM整流，从而使输入电流能跟随输入电压正弦变化，功率因数接近为1，同时输出稳定的直流电压；C，D半桥用于直流输出电压的二次纹波抑制，通过控制C，D两桥，使电容C1中储存的能量变化，当满足式（8）时，即可实现输出电压的二次纹波抑制。

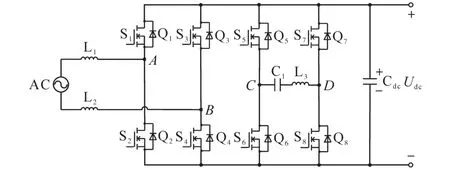
图4 传统的单相整流有源滤波拓扑Fig.4 The topology of the traditional single-phase active power filter

本文使用的有源滤波拓扑将图3中的B，C两相合并。合并后的B相同时要用于单相PWM整流和直流电压二次纹波抑制。此拓扑较传统方法减少了一个桥臂，在硬件成本降低的同时，减少了开关管的开关损耗，提高了变换器的效率和稳定性。对图4中的拓扑进行简化，合并中间2个半桥，得到如图5所示的拓扑，A相仅用于单相PWM整流；B，C两相均复用于单相PWM整流和有源滤波。

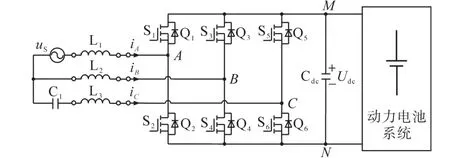
图5 电动汽车单相整流充电时的有源滤波拓扑Fig.5 The active filter topology for single-phase rectifying charging system of EVs

本文采用的有源滤波拓扑可看作是在三相PWM整流系统的基础上，加入1个储能电容，但不同的是，在三相PWM整流器中，三相电网电源对称且均能输入有功功率；而在此有源滤波电路中，只有一相能输入有功功率。本文所提出的控制方法通过控制滤波电容C1的电压，可使无功功率被电容吸收，从而达到抑制直流侧二次纹波的目的。

2 有源滤波拓扑控制策略

2.1 单相整流控制策略

如上所述，拓扑可分为两部分，即单相PWM整流和直流侧二次纹波抑制两部分，控制方法也对应为整流和二次纹波抑制两部分。图6为图5中的有源滤波拓扑的等效电路。图6中，L1，L2，L3分别为三相输入电感；uAN，uBN，uCN分别为三相半桥中点对直流输出负极N点的电压。

图6 有源滤波拓扑等效电路Fig.6 Equivalent circuit of the active power filter topology

系统的首要控制目标是实现直流侧电压的可控输出及输入侧功率因数为1，所提出的控制方法单相整流部分采用传统的电压、电流双环控制策略，控制框图如图7所示，此时单相整流拓扑的等效电路如图8所示，其对应的电路方程如下：

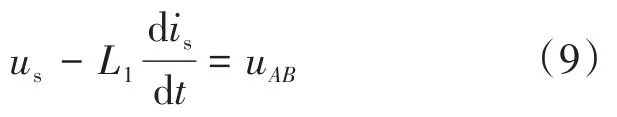
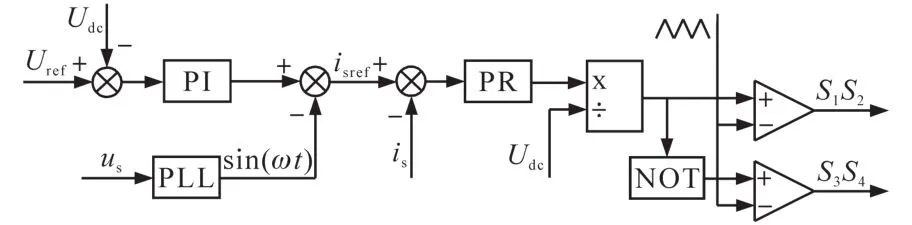
图7 传统单相PWM整流控制框图Fig.7 The block diagram of the traditional single-phase PWM rectifier control

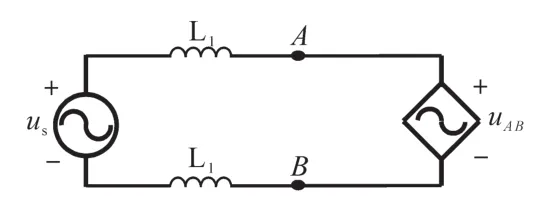
图8 传统单相PWM整流拓扑等效电路Fig.8 Equivalent circuit for the topology of the traditional single-phase PWM rectifier

图7中电压环通过PI调节直流电压与直流给定电压的差值为0，从而实现稳定的直流电压输出。电压环PI输出1个电流给定幅值，通过乘以经锁相环得到的、与电网输入电压相位相同的幅值为1的相位量，得到交流输入电流的给定值，即isref。电流环采用准比例谐振（proportional reso⁃nant，PR）控制器，利用准PR调节器对特定频率交流信号的高增益，可实现输入交流电流跟随给定值，且无稳态误差，从而实现输入侧功率因数接近于1。

2.2 有源滤波控制策略

设有源滤波理想情况下电容电压uC1表达式为

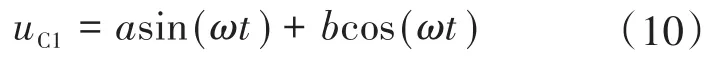
式中：a，b分别为电容电压 uC1的 sin（ωt）项和cos（ωt）项的幅值给定量。

则iC1对应为下式：

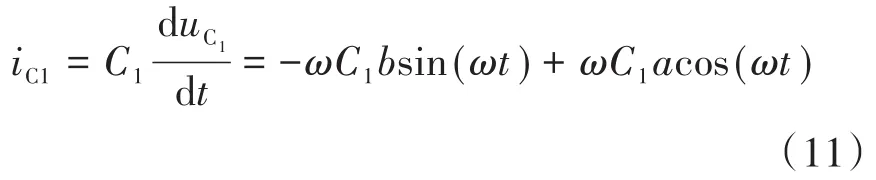
则可得储能电容的功率PC1为

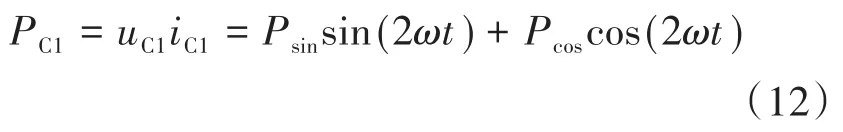
其中

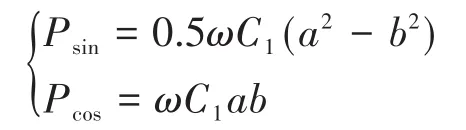
通过式（8）可得：

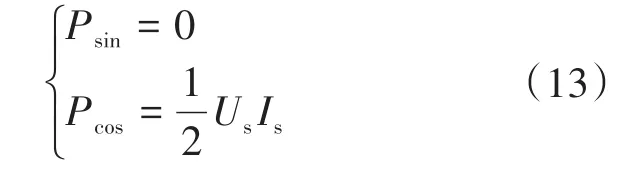
同时a，b的表达式设置如下：

根据式（14）可得到对应电容电压uC1的表达式为

在每个控制周期中，都可将储能电容视为一个电压源。则可得到有源滤波拓扑结构的等效电路，及其整流部分、有源滤波部分的工作模式，如图9所示。由图9可得到整流下的等效电压ucm和有源滤波下的等效电压udm满足如下关系：

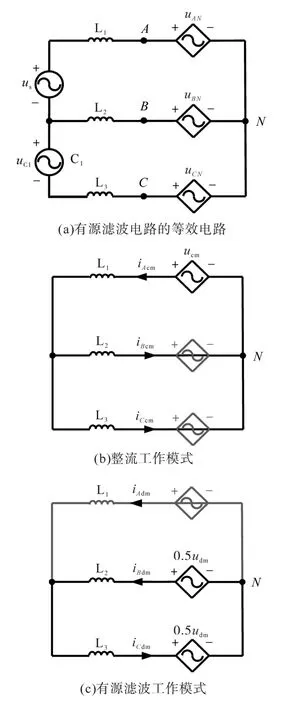
图9 有源滤波拓扑结构的等效电路及其工作模式Fig.9 Equivalent circuit of the active power filter topology and its working modes

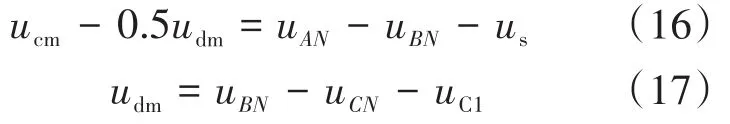
且对应设置uAN=-uBN则可得：

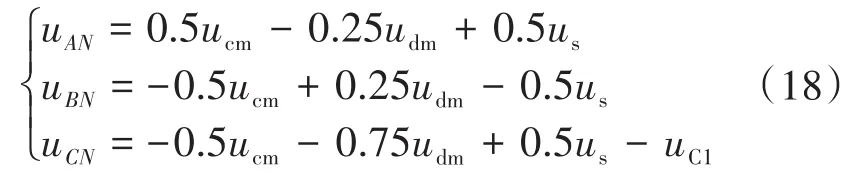
把电容C1也视为电压源时，则对应可得到控制框图如图10所示。

图10中，ucm对应的控制原理图同传统单相PWM整流相似，而udm对应的控制原理图如图11所示。

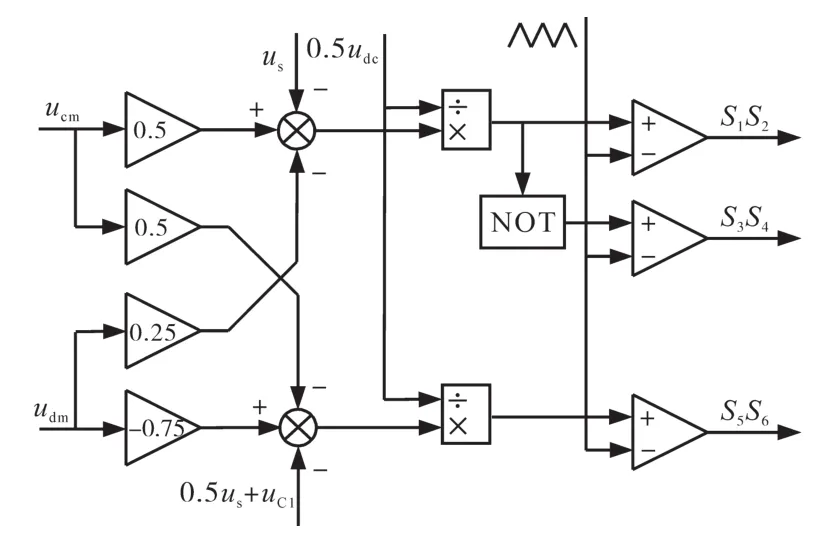
图10 有源滤波控制框图Fig.10 Block diagram of the active power filter control

图11 有源滤波分量udm的控制框图Fig.11 Control block diagram of udm

以式（15）的计算结果作为电容电压给定值，在控制环中，使用电压电流环控制，以达到良好的控制效果。

3 仿真与实验结果分析

在所提出的单相PWM整流的直流侧二次纹波抑制控制方法仿真中，使用的是理想开关器件，其余参数设计如下：电网侧输入电压峰值Us=110 V，整流器直流电压给定Udcref=220 V，A相电感L1=4 mH，B相电感L2=4 mH，C相电感L3=4 mH，储能电容C1=150 μF，直流稳压电容Cdc=200 μF，开关频率fs=10 kHz；直流侧等效负载电阻RL=100 Ω。

3.1 未采用有源滤波方法的单相整流仿真

在未采用有源滤波方法下，采用传统单相PWM整流拓扑时的输入输出仿真波形如图12所示。

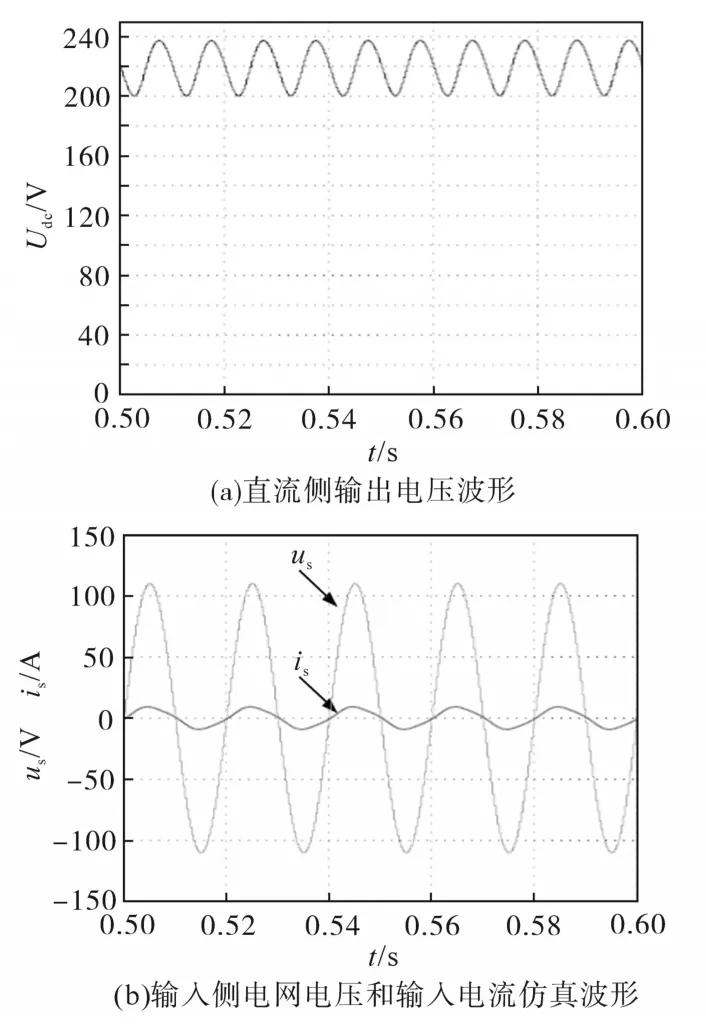
图12 未采用有源滤波方法单相PWM整流电路的仿真波形Fig.12 Simulation waveforms of the single-phase PWM rectifier without active power filter

由图12可见，未采用有源滤波方法时，单相整流器能实现输出给定的直流电压，并实现输入电压电流的相位差接近于0。但是，在直流侧输出电压的平均值Udc=219.464 V时，其输出电压的纹波为ΔUdc=37.558 V，输出电压波动较大，占给定输出电压的17.07%。输入电流虽然能实现跟随输入电压相位，但其畸变较大，THD=7.72%。其傅里叶分析图如图13所示。

由图13可知，输入电流的三次谐波较大，使得电流发生畸变。由于在单相PWM整流的控制回路中，输入电流的幅值给定是由直流输出电压的误差信号经PI调节得到的，当直流电压二次脉动较大时，直流电流的幅值量给定值中会相应的引入二次脉动。输入电流的给定值是由锁相环产生的电网电压的sin（ωt）和电压环PI输出相乘得到的，因而会使得电流给定值中含有三次谐波分量，导致电网电流畸变。而一般电网要求用户的输入交流电流THD在5%以内，可见此时电流畸变过大，不满足电网要求。

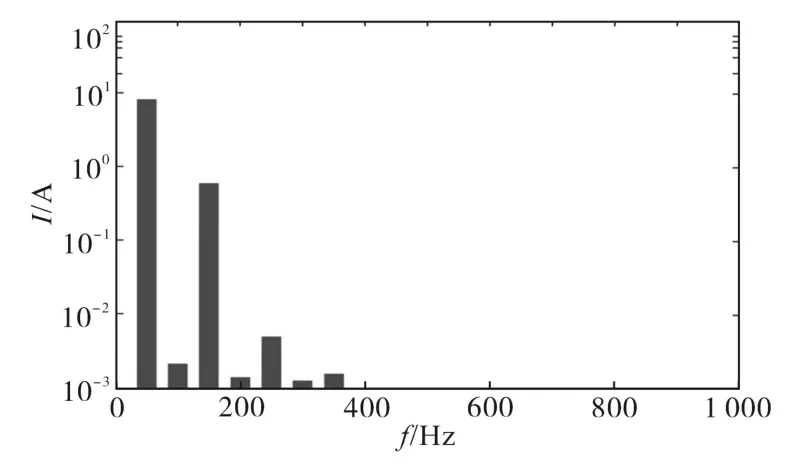
图13 未采用有源滤波时输入电流的傅里叶分析Fig.13 FFT analysis of the input current without active power filter

3.2 采用传统的有源滤波方法的单相整流仿真

采用如图4所示的传统有源滤波方法的单相PWM整流的输入输出仿真波形如图14所示。由图14a可知，传统的有源滤波电路具有直流侧电压纹波抑制功能，电压纹波为ΔUdc=10.732 V。由图14b可知，输入电流能跟随输入电压正弦变化，同时输入电流的傅里叶分析如图15所示。由图15可知，电流的THD=3.924%，电流控制效果较未采用有源滤波方法有了明显的改善。

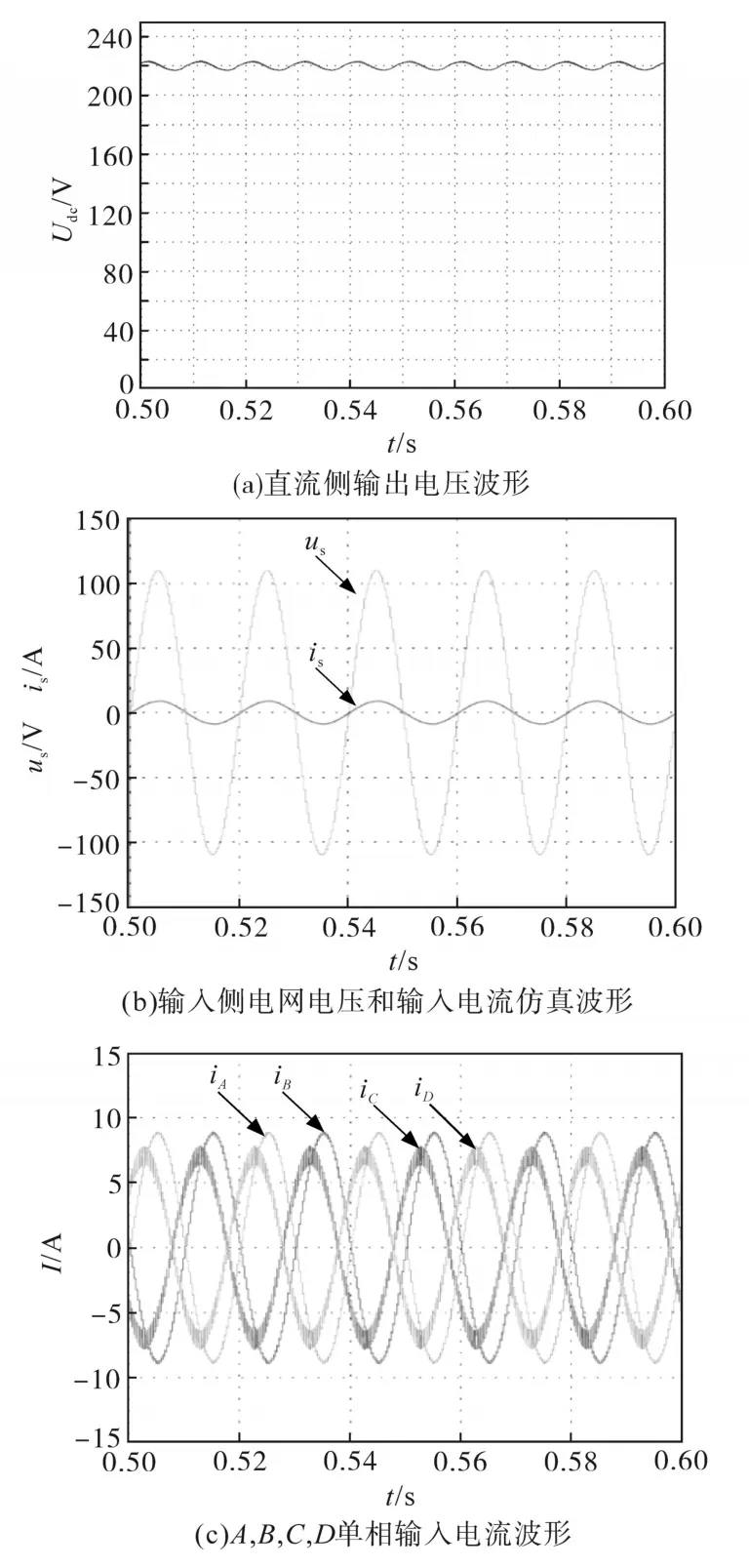
图14 采用传统有源滤波方法单相PWM整流电路仿真波形Fig.14 Simulation waveforms of the single-phase PWM rectifier with the traditional active power filter

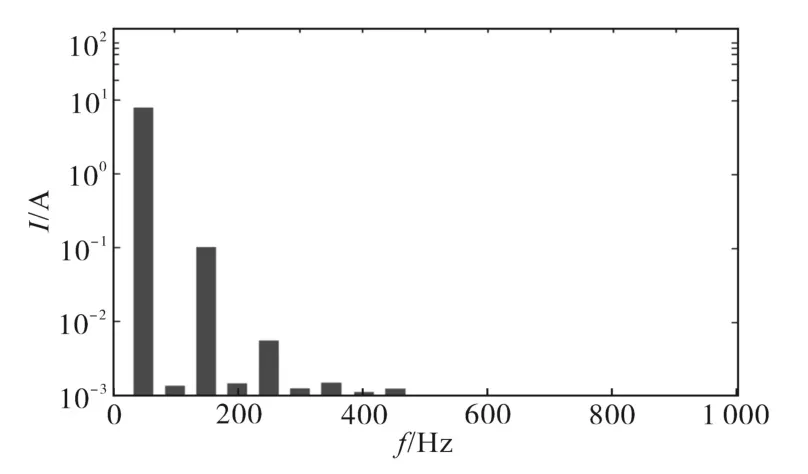
图15 采用传统有源滤波方法输入电流的傅里叶分析Fig.15 FFT analysis of the input current with the traditional active power filter

3.3 采用所提出的有源滤波方法的单相整流仿真

采用所提出的有源滤波方法的单相PWM整流的输入输出仿真波形如图16所示。由图16a可知，电路直流侧能输出稳定的直流电压，且此时电压纹波仅为ΔUdc=5.382 V。输出电压的纹波明显小于未应用有源滤波时，也小于采用传统的有源滤波方法时的纹波，仅占输出电压的2.45%，是未使用有源滤波时的纹波的0.15倍。

由图16b可知，输入电流能跟随输入电压变化，实现功率因数接近于1。其输入电流的傅里叶分析如图17所示，电流的THD=1.289%<5%，满足电网对用户的要求。图17中，电流三次谐波从未采用有源滤波时的0.657 A减小至0.082 0 A，电流的THD显著减小。与本节中的分析一致，输出电压的二次纹波减小导致电流的三次谐波减小，进而使得输入电流的THD减小。而本文所提出的有源滤波方法的输入电流谐波分量相比于传统有源滤波方法也有所减小。

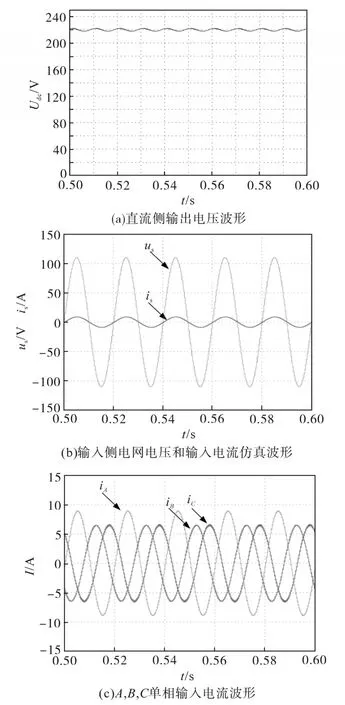
图16 采用有源滤波方法单相PWM整流电路的仿真波形Fig.16 Simulation waveforms of the single-phase PWM rectifier with the proposed active power filter

图17 采用有源滤波方法输入电流的傅里叶分析Fig.17 FFT analysis of the input current with the proposed active power filter

由图16c可知，相比于传统单相有源滤波拓扑，A相半桥的电流应力不变，但由于省去了D相半桥，同时B，C两相的电流应力减小，可见所提出的有源滤波控制方法可在节省充电器成本的同时，降低电路的损耗。

3.4 实验结果分析

依照仿真所设置的参数，本文进行实验以验证所提出的有源滤波方法的性能。为验证其直流侧二次纹波抑制性能，在相同参数下进行了与未使用有源滤波方法的单相整流实验作为对比，实验对比结果如图18所示。本文实验系统中输入电压有效值为110 V。

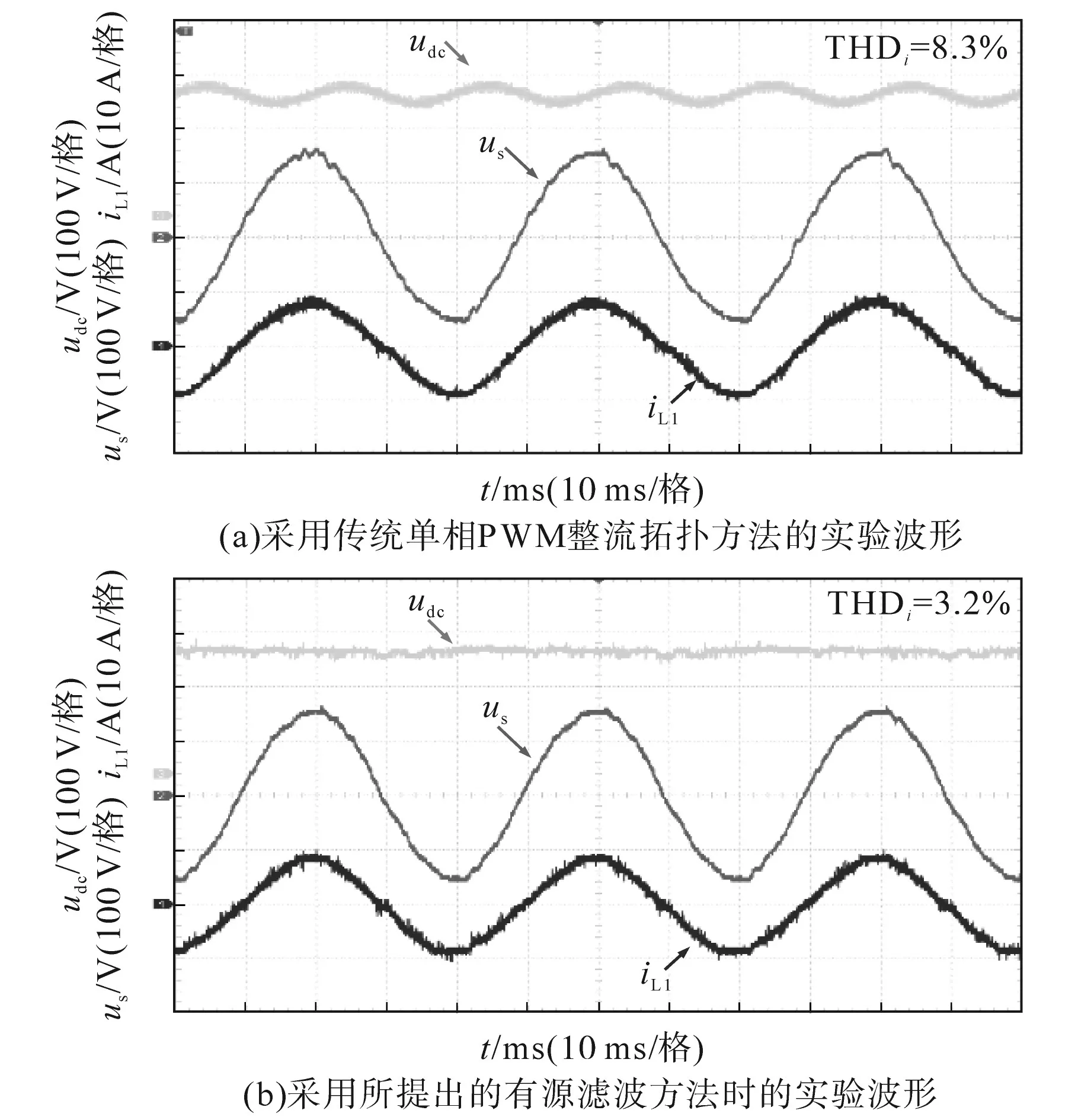
图18 两种控制方法实验波形对比Fig.18 Experimental waveforms contrast of the two methods

由图18可见，采用传统的单相PWM整流拓扑时，功率因数PF为0.996，THDi=6.7%，直流输出电压的二次脉动Δudc约为55 V。当采用所提出的有源滤波拓扑时，功率因数PF增加至0.998，THDi减少到2.8%，且此时直流输出电压的低频波动Δudc约减小到10 V。图19为额定负载时，采用和未采用有源滤波方法的两种整流器输入电流的傅里叶分析。与传统单相整流拓扑相比，采用本文所提出的有源滤波拓扑时，输入电流的三次谐波电流分量减少了50%以上，故此输入电流的总谐波畸变率减小了5.1%。可见，本文所提出的有源滤波方法可实现直流侧二次纹波抑制功能，同时降低输入电流的THD，提高整流器的网侧电能质量。

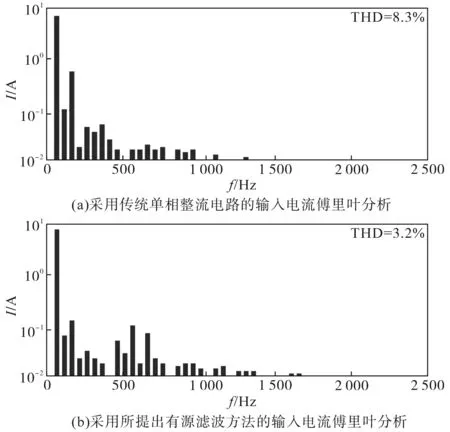
图19 两种方法的输入电流傅里叶分析对比Fig.19 FFT analysis contrast of the input current with the two methods

4 结论

本文在传统的单相有源滤波电路的基础上，分析使用了一种新型有源滤波拓扑并提出相应的控制方法，用于单相PWM整流的直流电压的二次纹波抑制。这种控制方法能实现通过复用半桥，控制电容储能，同时完成PWM整流和有源滤波。能实现输入电流跟随输出电压呈正弦且功率因数接近于1变化，输出稳定的直流电压，并能显著减小输出电压纹波。与此同时，减小输入电流畸变，改善网侧输入电流的THD。本文中搭建的仿真模型所得出的仿真和实验结果验证了所提控制方案原理的正确性和有效性。因此，本文所提出的有源滤波控制方法可以用于单相PWM整流的直流输出电压二次纹波的抑制。