逆变侧电流反馈的LCL型并网逆变器陷波超前补偿方法

（国网重庆市电力公司经济技术研究院，重庆 401120）

近年来，随着传统能源的枯竭，我国开始大力发展绿色友好型的可再生能源，其中新能源光伏发电技术在我国能源发展上的重要性日益凸显[1-2]。LCL型并网逆变器作为电网与光伏发电系统之间的核心接口设备，对入网电流质量具有重大影响[3-5]。如今LCL型并网逆变器主要采用两种控制结构[6]：1）进网电流反馈控制。该控制结构直接保证了进网电流的质量，拥有良好的抗扰性能、动态响应能力以及并网功率因数，但是需要添加额外的电容电流反馈回路，增加系统阻尼用以抑制LCL滤波器的谐振，否则系统将难以稳定[7]；2）逆变侧电流反馈控制。该控制结构可以保护功率开关管，限制电流纹波的功能，并且合理设计系统参数可使得单逆变侧闭环反馈控制是一个稳定的系统[8]，无需额外的回路抑制LCL滤波器的谐振，具有节省传感器，控制结构简单的优点，在实际工程中，出于保护设备的功率开关管的目的，大多场合采用逆变侧电流反馈控制，但该控制结构在数字控制下难以兼顾良好的系统动态响应能力和鲁棒性，在LCL谐振峰附近的三次截止频率处通常存在相位裕度过低的情况，大幅放大了该频率处的高频谐波，从而不满足国家规定的并网标准。

文献[9]表明单逆变侧闭环反馈控制结构容易稳定，但是该文献忽略了控制延时，控制延时带来的相位滞后影响会导致高频段截止频率处的相位裕度极大衰减，甚至可能引发系统失稳。文献[10]针对该控制结构提出了一套LCL滤波器参数优化设计方法，但是仍然无法避免高频谐波放大的问题，并且通过调整LCL滤波器参数来减小高频谐波含量会牺牲系统的动态响应能力。另外，提高采样频率也可较好地改善此问题，但是增大了数字信号处理器的负担[11]，目前，国内外学者针对逆变侧电流反馈控制结构的高频谐波放大问题还未得到较好的解决方案，因此有必要进一步研究改善该系统控制性能的方案。

本文以逆变侧电流反馈的单相LCL型并网逆变器为研究目标，首先搭建了LCL型并网逆变器的控制模型，并分析了数字控制下该系统结构中高频谐波的放大机理，提出一种基于陷波器的相位超前补偿方法，通过对陷波器参数的详细设计，实现了LCL谐振峰附近相位曲线的补偿，同时该方法又不影响系统的低频带宽与高频滤波功能，使得系统能兼顾良好的动态响应能力及鲁棒性，最后搭建了仿真平台进行验证。

1 基于逆变侧电流反馈的LCL型并网逆变器控制模型

基于逆变侧电流反馈的单相LCL型并网逆变器的控制结构如图1所示，整个系统主要由光伏发电端、电压源型并网逆变器以及LCL滤波器构成，在电路硬件中，Udc为光伏发电端产生的直流母线电压；S1，S2，S3，S4为 IGBT开关管；Uinv为逆变器输出电压；L1，C，L2分别为LCL滤波器的逆变侧电感、滤波电容以及网侧电感；iL，ic，ig分别为逆变器的输出电流、电容电流以及进网电流；ug为公共电网，在控制软件中，I*为参考电流幅值；PLL为锁相环模块；iref为参考电流；Gc为电流控制器。

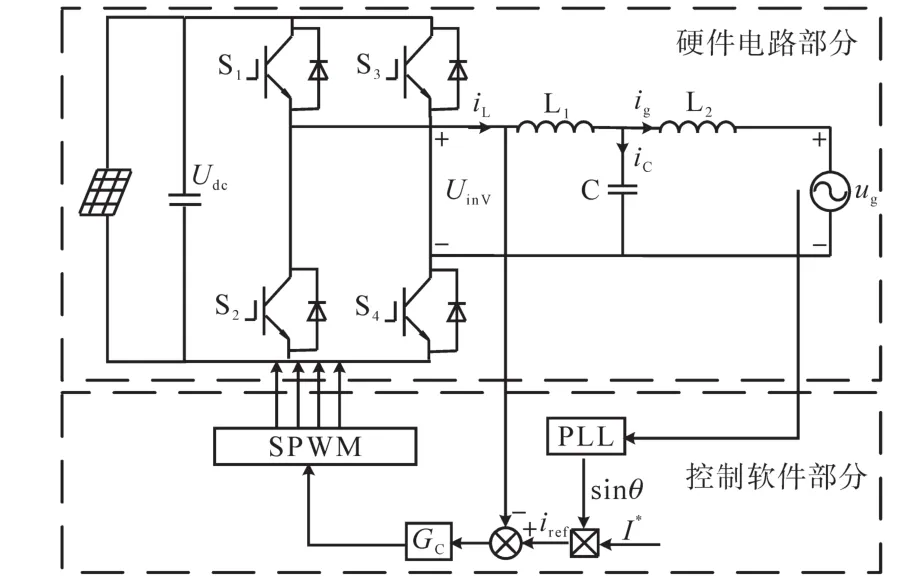
图1 基于逆变侧电流反馈的LCL型并网逆变器控制结构Fig.1 Control structure of LCL grid-connected inverter based on inverter-side current feedback

图2为基于逆变侧电流反馈的LCL型并网逆变器的控制框图，其中，Kpwm为逆变环节的等效增益（直流母线电压Udc与三角载波幅值Utri之比[12]），Gd（s）为数字控制下的延时环节，主要由软件控制部分中系统算法运算引起的一拍延时和零阶保持器引起的半拍延时组成[13]，其连续域下的表达式可等效为

图2 LCL型并网逆变器的控制框图Fig.2 Control block diagram of LCL-type grid-connected inverters

式中：Ts为采样周期。

若忽略图2中公共电网ug（s）的扰动，参考电流iref（s）至iL（s）的开环传递函数如下：

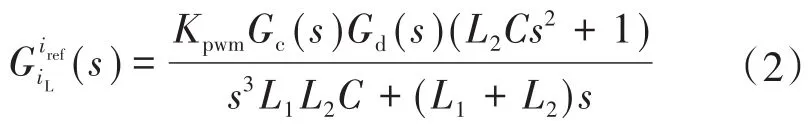
同时由式（2）可知，该系统存在一对共轭零点和一对共轭极点，表明该系统环路增益的幅频特性和相频特性都将产生两次跳变，其跳变频率为

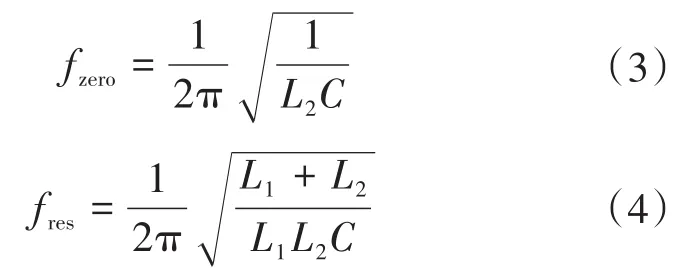
图3分别给出了系统考虑延时环节和未考虑延时环节下的波德图，由图3可见，数字控制下的延时环节给系统相频特性带来了极大改变，通过对比发现，在图3a中，由于延时环节的高频相位滞后影响，在系统的三次截止频率f3处明显存在相位裕度过低的情况，造成该频率的分量大幅放大，恶化了输出电流质量，而图3b中，f3处系统相位裕度总是充足的，系统输出电流质量良好，这主要是由于延时环节的引入，导致系统在采样频率 fs的 1∕6 处相位曲线穿越-180°[14]，若 f3接近 fs∕6，则必然导致f3处的相位裕度过低，虽然通过减小LCL谐振频率fres可以缓解此情况，但是改善效果较差，不足以较好地抑制该点高频谐波的放大，并且调整LCL参数可能带来电容无功功率的增大，系统动态响应能力削弱等问题，故在数字控制下，该问题严重增大了系统的设计难度，限制了系统参数的选取。

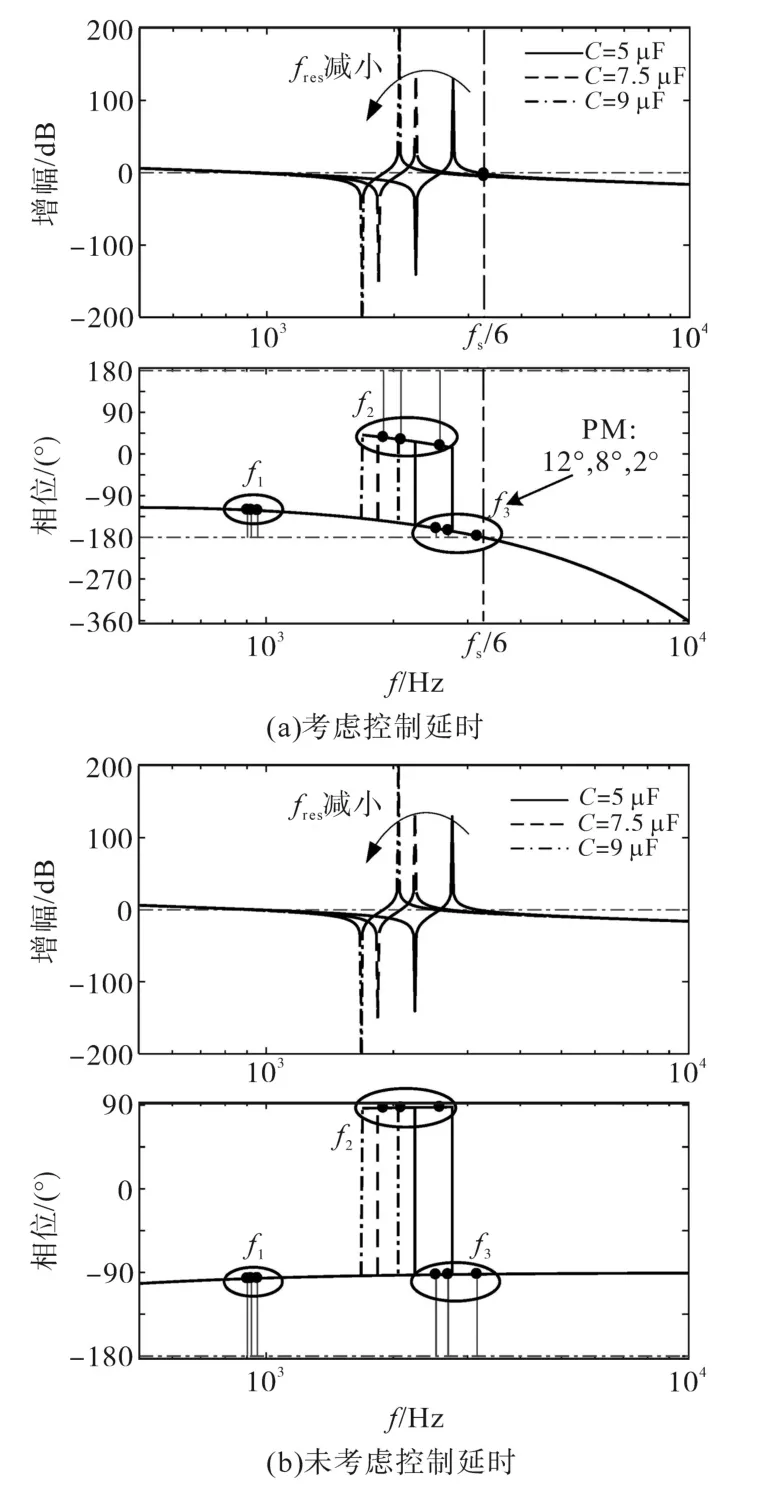
图3 延时环节Gd（s）对系统开环波德图的影响Fig.3 The influence of delay link Gd（s）on the open loop Bode diagram of the system

2 陷波超前补偿方法

2.1 相位超前补偿环节

解决该问题的主要思路就是对f3处的相位裕度进行补偿，典型的相位超前补偿环节能对特定频率进行较大相位的补偿，经常被广泛应用于各种场合，其表达式为

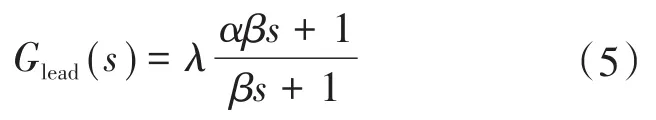
式中：λ，α，β为补偿环节参数，α>1。

其波德图如图4所示，但是该环节存在较大缺点，在相位超前频段将引入幅值增益，若此环节应用在该系统中，将f3设为相位最大补偿点fmax，虽然能有效抑制f3处高频谐波的放大，但却严重衰减环路增益中高频滤波功能，其应用价值有限，应当寻求更优良的解决方案。

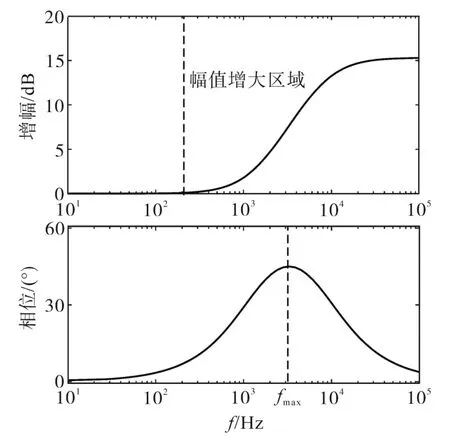
图4 相位超前补偿环节Glead（s）波德图Fig.4 Bode diagram of phase lead compensation link Glead（s）

2.2 陷波超前补偿方法的实现机理

如前文所述，我们希望寻求一种不改变原系统环路增益或者影响极小的方法，仅对f3附近的相位裕度进行改善，而基于陷波器的超前补偿方法可以满足所提要求，引入陷波器后的系统控制框图如图5所示。

图5 引入陷波器后的系统控制框图Fig.5 The system control diagram after introducing the notch filter

图5中，Gn（s）为用于提高f3处相位裕度的陷波器，其波德图如图6所示，其传递函数如下：

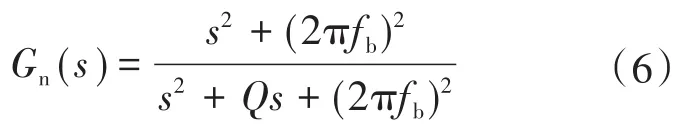
式中：Q为品质因数；fb为陷波频率。

如图6所示，陷波器Gn（s）在大于陷波频率fb的一定频段内处提供了相位超前的功能，若将f3设定在相位超前区域内的频率，即可实现对f3处相位裕度的补偿，但是同时陷波器在小于fb内的一定频段内提供了相位滞后的功能，并且在fb处发生幅值跌落，所以在系统中引入陷波器时，应合理清晰地设计陷波器参数，若陷波频率fb设定为LCL谐振峰内大于0 dB内的频率时，幅值跌落会穿越0 dB线，导致0 dB线对应的相位裕度可能小于0°，引发系统不稳定。

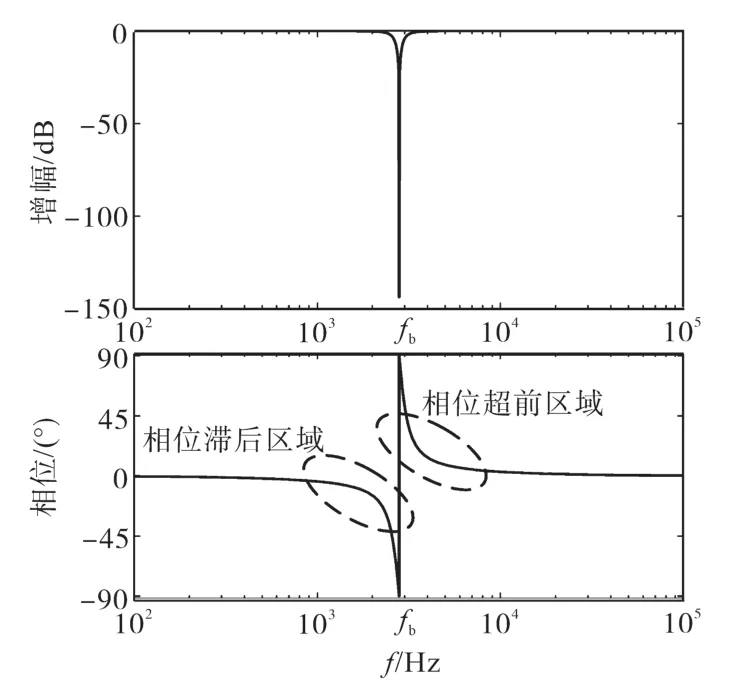
图6 陷波器Gn（s）的波德图Fig.6 Bode diagram of notch filter Gn（s）

2.3 陷波器的参数设计

在设计陷波器参数的过程中，第一步应当确立陷波频率fb，陷波频率fb应当满足三个条件：

1）为了满足f3处相位裕度的补偿，fb首先应当小于f3，另外，如上节所述，为了防止引入陷波器后，系统发生失稳，陷波频率fb的选择应当选择环路增益中小于0 dB的频率，故fb应小于f2；

2）为了不影响系统的低频增益，陷波频率fb应当大于系统环路增益的一次截止频率f1；

3）在并网逆变器的实际运行过程中，滤波电容C的参数会产生较大的数值变化，通常变化范围为±20%，为了防止滤波电容C波动时，导致陷波频率fb大于系统的二次截止频率f2，应当考虑到滤波电容C波动到最大值时的情况，同时为了保留一定的安全裕度，陷波频率fb应当小于或等于滤波电容C在+30%波动时的LCL谐振频率，记为fr_min；

综上所述，陷波频率fb的选择应当满足下式的约束条件：

第二步应当确立品质因数Q，品质因数Q关乎到f3处相位补偿的效果，Q的选取应当满足以下两个条件：

1）为了良好抑制f3处高频谐波的放大，要求相位裕度尽量大于25°；

2）陷波器的相位滞后区域可能会造成截止频率f1处的相位裕度下降，为了不影响系统的鲁棒性，要求陷波器在f1处的相位滞后不超过10°；

综上所述，品质因数Q的选择应当满足下式的约束条件：

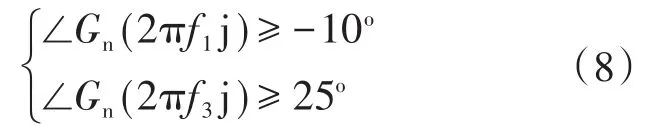
将s=2πf1j与s=2πf3j代入式（8），同时陷波频率fb取fr_min，经过求解后得出：

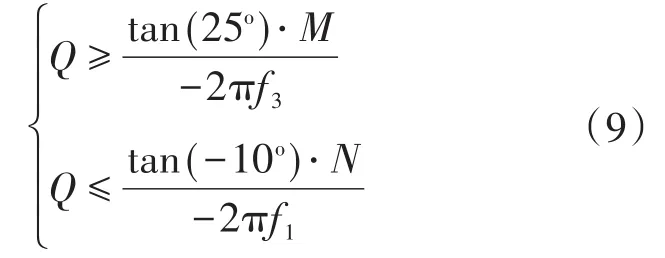
其中

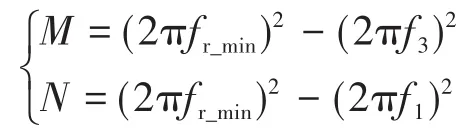
2.4 设计实例

本文依照经典文献[15]设计了合适的单相LCL型并网逆变器的系统参数，具体为：直流母线电压Udc=400 V，电网电压ug=220 V，开关频率fsw=10 kHz，采样频率fs=20 kHz，逆变桥增益Kpwm=400，输出功率Po=3 kW，开环增益kp=0.048，积分增益kr=10。

下面针对以上系统参数进行陷波超前补偿方法的设计，同时电流控制器Gc选用经典的准PR控制器，其传递函数如下：

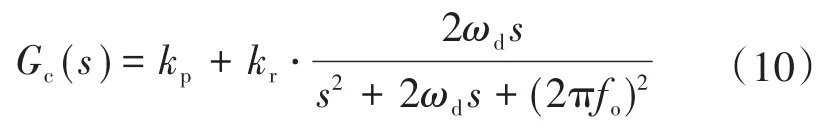
式中：ωd为阻尼系数，通常为π；fo为基波频率。

在系统低频段内，环路增益的高阶项基本不起作用，可以忽略，通过简化开环传递函数，系统的一次截止频率f1可以近似由下式表达：

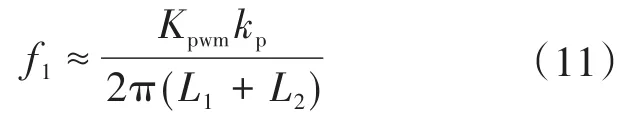
由于系统三次截止频率f3位于系统高频段，此时环路增益中高阶项作为主导项，不可忽略，通过系统开环传递函数来表示f3，则求解难度太大，而本文通过系统开环波德图对f3进行反复多次校验，最终确定f3近似可以由fres表示如下：

1）选择第一组LCL滤波器参数：逆变侧电感L1=2 mH，滤波电容C=5.5μF，网侧电感L2=1 mH，fres≈2 600 Hz，通过式（11）、式（12）确定出f1≈1 000 Hz，f3≈3 100 Hz，陷波频率fb选择fr_min≈2 300 Hz，通过式（9）确定出陷波器品质因数Q的取值范围：1 300π≤Q≤1 500π，本文折中选取1 400π。原系统引入本文所提方法前后的开环波德图如图7a所示，本文所提方法考虑滤波电容C在±20%波动时的开环波德图如图7b所示。

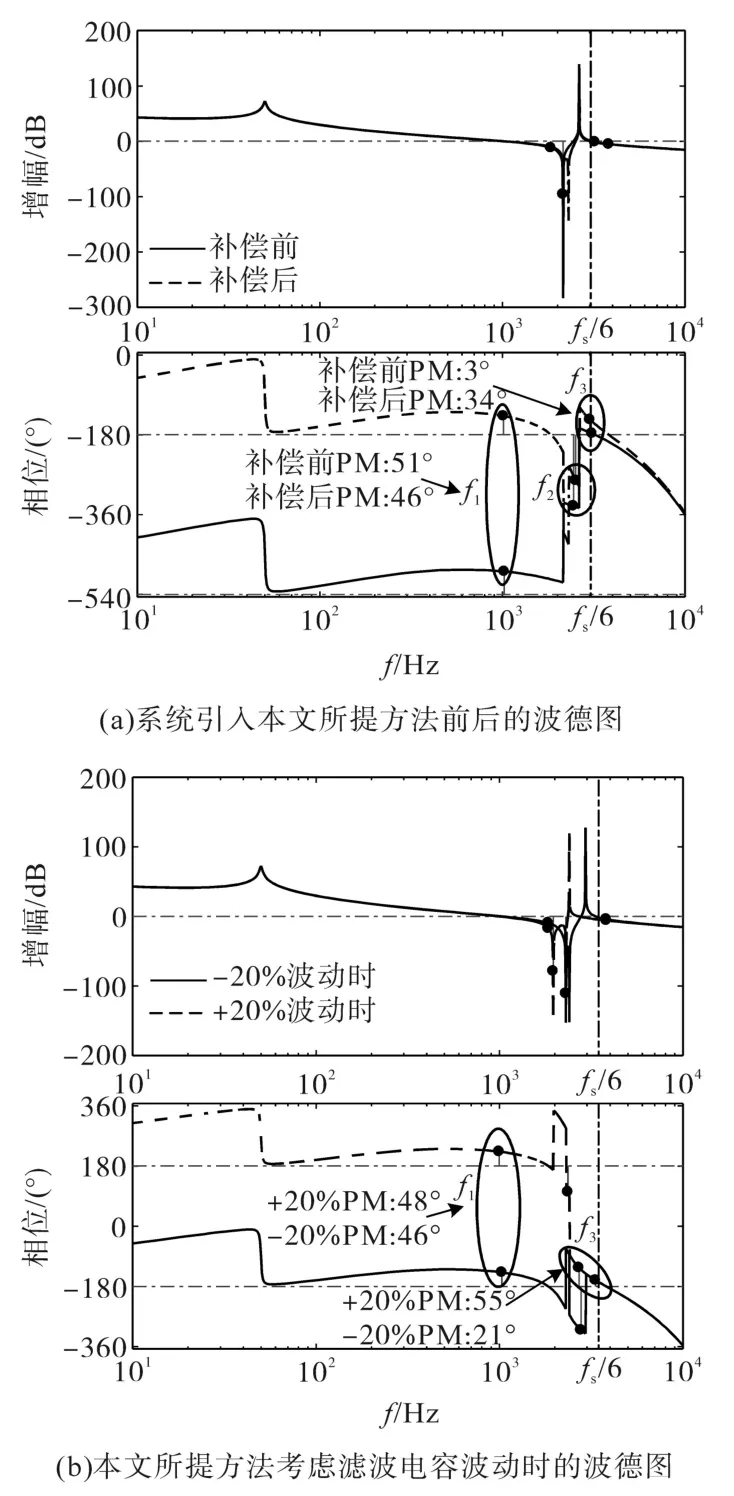
图7 第一组滤波器下的系统波德图Fig.7 The Bode diagram of the system under the first set of filters

2）选择第二组LCL滤波器参数：逆变侧电感L1=2 mH，滤波电容C=7.5μF，网侧电感L2=1 mH，fres≈2 250 Hz。

同样的，通过式（11）、式（12）确定出f1≈1 000 Hz，f3≈2 700 Hz，陷波频率fb选择fr_min≈2 000 Hz，通过式（9）确定出陷波器品质因数Q的取值范围：980π≤Q≤1 050π，本文折中选取1 000π。原系统采用本文所提方法前后的开环波德图如图8a所示，本文所提方法考虑滤波电容C在±20%波动时的开环波德图如图8b所示。

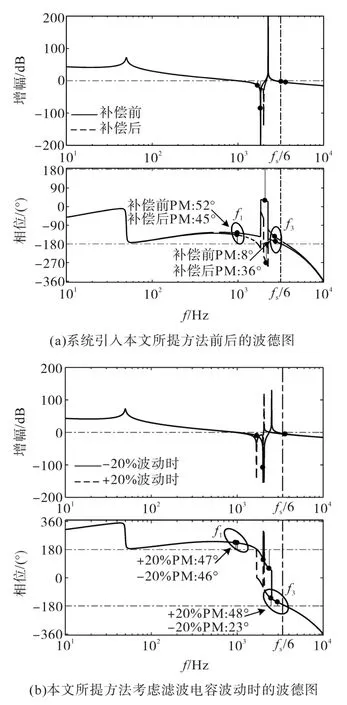
图8 第二组滤波器下的系统波德图Fig.8 The Bode diagram of the system under the second set of filters

经过上述两组不同的设计实例表明，原系统在引入本文设计的陷波器后，其环路增益在f3处的相位裕度得到了大幅提升，而f1处的相位裕度以及系统的幅频特性基本不受影响，很好地满足了前文提出的期望条件，说明该设计思路正确，同时，本文提出方法也能很好地应对滤波电容发生波动的情况，始终保证了系统在f3处有足够的相位裕度，有效抑制了f3处高频谐波的放大，使得原本不满足并网要求的系统参数也可输出电能质量良好的电流，加强了系统参数对该控制结构的适应性。

3 仿真验证

本文通过Matlab∕Simulink仿真软件搭建了一套基于逆变侧电流反馈的单相LCL型并网逆变器系统模型，系统参数同2.4节，与上节分析方式类似，将LCL滤波器设置为两组不同参数，分别对本文所提策略进行验证，图9为第一组LCL滤波器参数下进网电流ig与公共电网ug的波形图，图10为第二组LCL滤波器参数下进网电流ig与公共电网ug的波形图，表1为系统在两组滤波器参数下，进网电流ig中高频谐波（谐波次数>33次）的最大含量情况，用基波幅值的百分比来描述。

图9 第一组滤波器下的并网波形图Fig.9 The grid-connected waveforms under the first set of filters

图10 第二组滤波器下的并网波形图Fig.10 The grid-connected waveforms under the second set of filters

当系统采用第一组LCL滤波器时，由于补偿前f3处相位裕度过低，导致进网电流ig中含有大量高频谐波，且最大含量为基波幅值的1.7%，不满足国家规定的并网标准，同样采用第二组LCL滤波器时，由于LCL谐振频率的降低，f3处的相位裕度有一定提高，该情况得到了一定缓解，但仍不满足并网标准。

当系统采用本文所提方法进行补偿后，在两组不同滤波器下都能输出高频谐波含量较低的进网电流，且高频谐波的最大含量都在基波幅值的0.3%以下，满足国家的并网标准，图9b、图10b为滤波电容C在实际运行中发生±20%波动时进网电流ig的情况，由表1不难发现本文所提策略在滤波电容C发生波动时始终能为f3处提供足够的相位裕度，高频谐波的抑制效果仍然令人满意，仿真结果表明了该方法的有效性与陷波器设计思路的正确性。

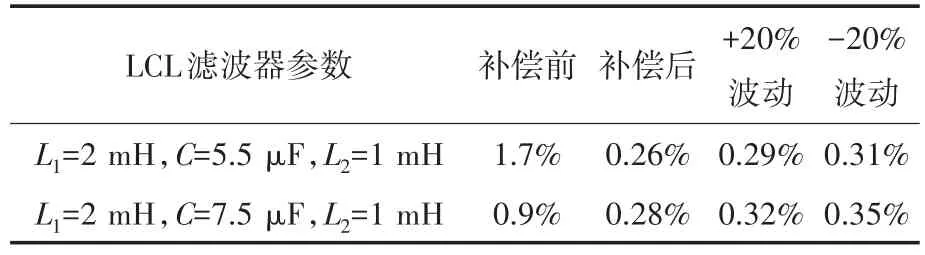
表1 高频谐波的最大含量情况Tab.1 Maximum content of high frequency harmonics

4 结论

在数字控制下，基于逆变侧电流反馈的LCL型并网逆变器系统容易产生高频谐波放大的问题，并且通过调整系统参数来解决该问题大幅增加了系统设计难度，且对原系统会产生不良影响，因此，本文提出一种基于陷波器的相位超前补偿方法，该方法在滤波电容宽范围波动的情况下也能提高系统三次截止频率处的相位裕度，有效抑制了该频率点高频谐波的放大，且该方法不影响原系统的动静态特性，避免了反复调整系统参数来限制高频谐波，下一步尝试将该方法拓展运用到三相并网逆变器或者多并联式的光伏集群电站中。