FOA-PID控制器在悬臂式掘进机截割头升降控制系统中的应用
熊媛媛
(四川化工职业技术学院, 四川 泸州 646099)
引言
悬臂式掘进机作为常用工程机械,主要承担煤矿巷道掘进任务[1]。其截割头升降的精确控制取决于升降液压缸,而目前的升降液压缸多采用电磁换向阀控制活塞杆输出位移,电磁换向阀控制精度不高,致使无法准确控制截割部升降,因此需要采用控制精度更高的换向阀以及控制性能更强的控制器,才能实现截割头升降精确控制。
李楠楠[2]针对悬臂式掘进机控制精度不足的问题,对系统采取了模糊自适应整定PID控制器进行校正,实验结果表明该控制器改进了系统的动态特性,取得了较好的控制效果;毛清华等[3]提出了一种基于PID控制的悬臂式掘进机截割头位置精确控制方法,实验结果表明:在加入PID反馈控制后,截割头位置控制精度大大提高,实现了煤矿悬臂式掘进截割头位置的精确控制;孙晓娜[4]利用控制系统仿真软件Simulink对悬臂式掘进机截割头电液比例位置控制系统进行仿真和PID校正,改善了系统的动态特性;王晓东等[5]提出了车体升降定位控制策略,设计了基于PLC(可编程逻辑控制器)控制的掘进机远程线控系统,试验结果表明了该控制策略的有效性;杨文娟等[6]针对悬臂式掘进机截割头姿态检测难题,提出一种利用视觉传感器识别红外标靶特征的截割头姿态测量方法,该方法的角度测量误差在0.5°范围以内,可以满足掘进机截割过程中截割头姿态角测量要求;汪胜陆等[7]针对悬臂式掘进机升降控制精度不高的问题,提出了运用电液比例方向阀代替手动换向阀的新改进控制方案,运用MATLAB软件对该系统进行闭环PID控制仿真,新改进的系统具有较好的控制品质;闫鲁超[8]建立了基于改进粒子群算法的掘进机掘进液压系统的自适应控制模型,基于该算法的控制策略具有较高的鲁棒性。
结合以上研究成果,建立了系统数学模型,采用果蝇算法和萤火虫算法对PID控制器进行参数优化,基于Simulink仿真比较了优化后的系统响应性能,并为了验证两种控制器实际控制性能进行了实验研究。
1 截割头升降控制系统数学建模
悬臂式掘进机截割头升降执行机构为升降液压缸,如图1所示,其可以控制截割头在垂直方向运动[9]。

图1 悬臂式掘进机截割头升降执行机构

图2 截割头升降控制系统工作原理
本研究将掘进机常采用的电磁换向阀换成控制精度更高的比例换向阀,则截割头升降控制系统如图2所示。分析该图可以得出,截割头升降控制系统为典型的阀控缸系统,阀控缸系统数学模型由3个基本方程组成[10]。
(1) 比例换向阀线性负载流量方程,建立方程前做如下假设:供油压力恒定,回油压力为0,则比例换向阀线性负载流量方程如下:
qL=Kqxv-KcpL
(1)
式中,Kq—— 流量增益,m3·m·s-1
xv—— 阀芯位移,m
Kc—— 流量压力系数,m3·Pa·s-1
pL—— 液压缸压力,Pa
液压缸流量连续性方程如下式所示:
(2)
式中,Ae—— 液压缸活塞有效工作面积,m2
Be—— 有效体积弹性模量,N·m-1
xp—— 活塞位移,m
Ctp—— 液压缸总泄漏系数,m3·Pa·s-1
V0—— 进油腔容积,m3
(2) 液压缸与负载力平衡方程,在负载弹簧力、惯性力、黏性阻力的共同作用下,力平衡方程可由下式表示:
(3)
式中,mt—— 活塞及负载折算到活塞上的总质量,kg
Bp—— 活塞及负载的黏性阻尼系数,kg·s-1
FL—— 负载干扰力,N
K—— 负载弹簧刚度,N·m-1
将式(1)~式(3)进行拉式变化并结合采煤机滚筒实际工况可得液压缸活塞杆总的输出位移为:
(4)
由式(4)可得活塞杆位移对阀芯位移的传递函数:
(5)
式中,wh—— 液压固有频率,rad·s-1
ξh—— 液压阻尼比
Kce—— 总流量压力系数
活塞位移对负载干扰力的传递函数为:
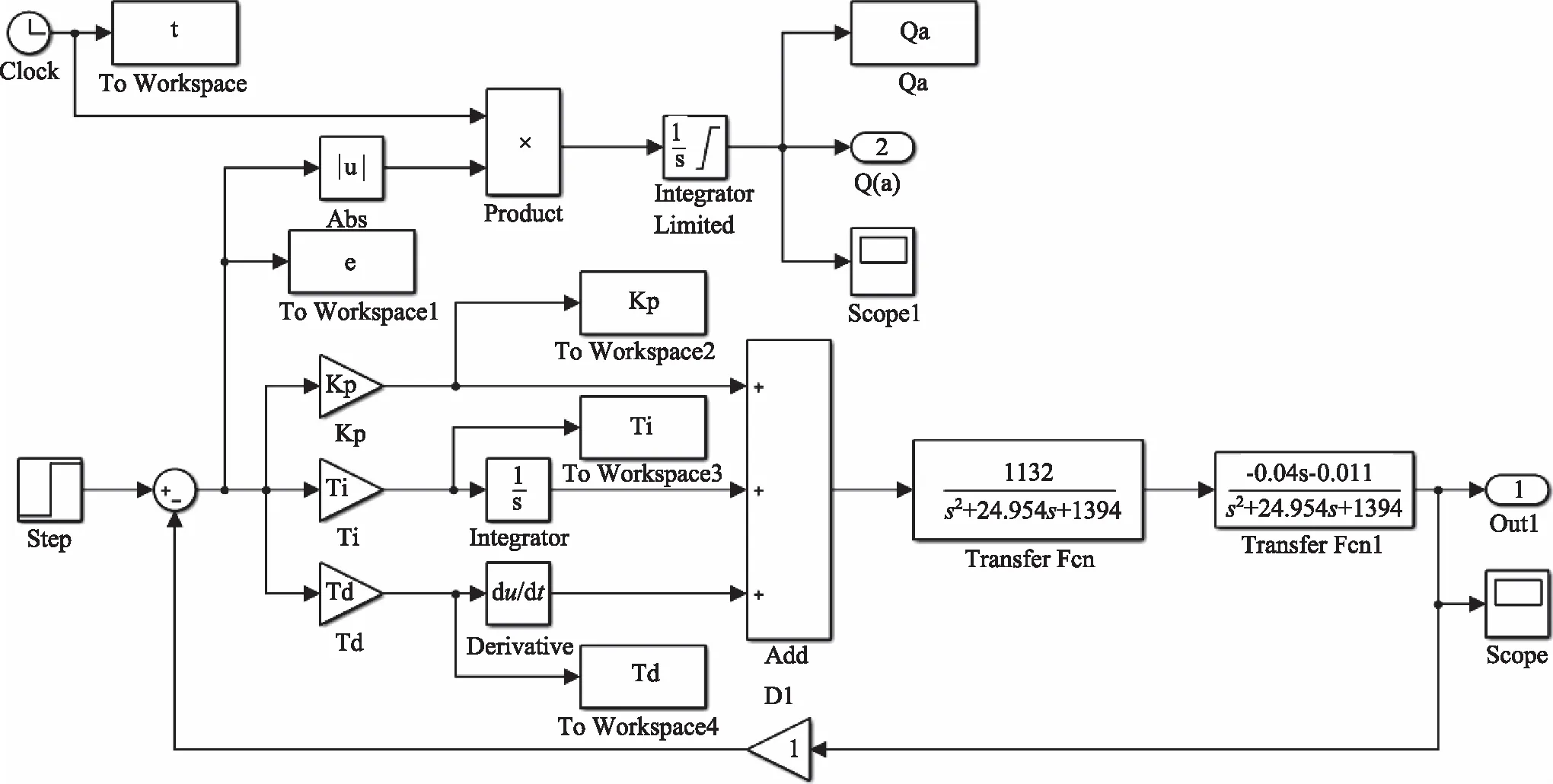
图3 PID参数优化过程的仿真模型
(6)
表1为截割头升降控制系统主要参数,截割头质心选取在升降液压缸活塞杆与截割头悬臂连接处。
将各参数代入式(5)和式(6), 活塞位移xp对阀

表1 技术参数
芯位移xv的传递函数为:
(7)
活塞位移xp对负载干扰F的传递函数为:
(8)
2 系统PID参数优化
比例换向阀存在中位死区特性,其可以造成系统响应滞后[11]。为实现高精度的截割头升降控制,就要对死区进行补偿。本研究采用静态补偿算法实现对死区的补偿,如式(9)所示:
U=U0+UC
(9)
式中,U—— 死区补偿后输出电压,V
U0—— 未补偿死区输出电压,V
Uc—— 死区补偿电压,V
Uc的选取遵循如下规则:当U0>0时,Uc=Uk1;当U0=0时,Uc=0;当U0<0时,Uc=-Uk1。式中Uk1为补偿电压常量,其取值近似等于死区幅值控制电压。
液压缸位置控制常采用PID控制器, PID控制器中最重要的是其3个参数的优化。下面分别采用萤火虫算法和果蝇算法优化PID参数。PID参数优化过程的仿真模型如图3所示。
首先采用萤火虫算法优化PID参数[13],其结构框

图4 萤火虫算法优化PID参数
图如图4所示。
在MATLAB中对萤火虫算法优化PID参数程序进行编写,部分程序如图5所示。

图5 萤火虫算法优化PID参数程序实现
参数设置如下:设置萤火虫种群规模n为30,初始荧光素L0为5,荧光素浓度挥发速度系数ρ为0.4,萤火虫个体更新速度系数γ为0.6,决策域范围更新系数初始值β为0.08,萤火虫的初始步长w(0)为0.03,最大迭代次数为100,最小移动步长0.0001,最大移动步长为1。采用ITAE作为适应度函数,如式(10)所示:
(10)
经过30代迭代,得到相应的适应度T迭代次数N曲线如图6所示。

图6 适应度迭代曲线(萤火虫算法)
优化后可获得萤火虫算法优化后的PID参数分别为:Kp=12.49,Ti=0.92,Td=0.05。
再次采用果蝇算法优化PID参数[14],如图7所示为其结构框图。

图7 果蝇算法优化PID参数
在MATLAB中对萤火虫算法优化PID参数程序进行编写,部分程序如图8所示。

图8 果蝇算法优化PID参数程序实现
具体过程如下:设置果蝇初始种群大小为30,迭代次数30。3个参数Kp,Ti和Td的初始取值为20, 0.6, 0.2,搜索范围设置为(0,150)。同样采用ITAE作为适应度函数。
经过30代迭代,果蝇适应度提高,得到相应的适应度迭代曲线如图9所示。分析图6和图9可知,用果蝇算法进行PID参数优化时,适应度函数收敛速度更快,更平缓的达到最优值。

图9 适应度迭代曲线(果蝇算法)
优化后可获得果蝇算法优化后的PID参数为:Kp=10.16,Ti=1.07,Td=0.08。

图10 截割头升降控制系统仿真模型
3 系统仿真
在Simulink中将经萤火虫算法和果蝇算法优化的PID参数加入到仿真模型中,如图10所示。
分别给出系统幅值为1 mm的阶跃信号以及不同频率的正弦信号,仿真结果如图11~图13所示。本研究为简化叙述,称萤火虫算法优化的PID控制器为FA-PID控制器,果蝇算法优化的PID控制器为FOA-PID控制器。

图11 阶跃信号
分析图11以及仿真数据可以看出,FA-PID控制器出现了较大的超调,而FOA-PID控制器超调量较小,并且FOA-PID控制器达到稳态值的速度更快。
分析图12、图13以及仿真数据可以看出, FA-PID

图12 0.25 Hz正弦信号
控制器以及FOA-PID控制器都能很好的追踪信号,但FOA-PID控制器在最大跟踪误差和平均跟踪误差方面优于FA-PID控制器。

图13 0.5 Hz正弦信号
4 实验研究
为了验证FOA-PID控制器能否应用于实际系统,在徐工EBZ200型悬臂式掘进机实验台上进行实验研究,如图14所示。

图14 徐工EBZ200型悬臂式掘进机实验台
实验系统原理如图15所示。系统工作原理简述如下:本系统采用流量控制,液压缸活塞杆的输出值由位移传感器采集并将该值反馈给PLC控制器,与系统给定位置值作比较,当两值存在偏差时,由PLC输出电压经比例放大器放大后控制比例换向阀开口量的大小,进而液压缸活塞杆运动,位置传感器不断反馈活塞杆实时位移值,当活塞杆实时位移值等于系统给定位置值时,活塞杆停止运动,进而实现对悬臂式掘进机截割头升降的控制。

图15 徐工EBZ200型悬臂式掘进机实验系统原理
实验所用液压泵参数为型号为力士乐A10VSO 80,排量为80 mL/r,额定转速为1500 r/min。比例换向阀主要参数为:型号为力士乐85-2X/G24K31,公称流量qv为85 L/min,最大允许流量为200 L/min,公称规格尺寸为15 mm。控制器采用西门子PLC300。位移传感器采用的是美国OMEGA的LVDT传感器。
分别给系统幅值为1 mm的阶跃信号以及不同频率的正弦信号,得到实验结果如图16~图18所示。

图16 阶跃响应试验曲线对比
分析图16以及实验数据可以看出,FA-PID控制器和FOA-PID控制器响应时间均在2.5 s左右,FOA-PID控制器的超调量略小于FA-PID控制器。系统达到稳态时,FOA-PID控制器存在0.05 mm的稳态误差,而FA-PID控制器存在0.07 mm 的稳态误差。

图17 0.25 Hz正弦响应试验曲线对比

图18 0.5 Hz正弦响应试验曲线对比
分析图17、图18以及实验数据可以看出,FA-PID控制器以及FOA-PID控制器都能很好的追踪实验信号,但FOA-PID控制器在最大跟踪误差和平均跟踪误差方面均优于FA-PID控制器,此结论和仿真结论相同。
5 结论
为提高悬臂式掘进机截割头升降控制精度,在建立系统数学模型数基础上,分别采用FA算法和FOA算法对PID参数进行优化,对FA-PID控制器和FOA-PID控制器控制性能进行了仿真分析,并为了验证两种控制器实际控制性能进行了实验研究。主要得出以下结论:
对于幅值为1 mm 的阶跃信号以及不同频率的正弦信号,FOA-PID控制器响应性能均优于FA-PID控制器, FOA-PID控制器更能满足悬臂式掘进机对于截割头升降控制精度的要求。

