双U形节流槽滑阀多场耦合特性研究
张 鑫, 韩 进, 马德建, 高庆利, 刘建超
(山东科技大学 机械电子工程学院, 山东 青岛 266590)
引言
液压阀是液压系统的主要控制元件,其性能对液压系统的正常运行具有关键性作用[1]。但是液压阀在工作过程中,阀芯会因为受热变形导致阀腔内的间隙变小,从而导致阀芯在运动过程中阻力变大,使滑阀工作不流畅,更严重的会使阀芯卡死,导致液压阀不能工作[2]。因此,研究液压滑阀多场耦合特性对改善滑阀工作特性,提高液压系统的可靠性具有重要意义。陈晓明等[3]对滑阀内流体的流动以及传热过程进行了数值模拟,为研究液压滑阀的卡紧现象提供了借鉴。
谢海波等[4]对阀芯所受液动力进行了数值求解,并对液压阀的压降曲线进行了比较,为液压阀的优化提供了指导。张俊俊等[5]对液压滑阀阀芯卡紧力进行了数值模拟研究,得到了均压槽合理的结构尺寸。晏静江等[6-7]对U形节流阀的速度场以及油液黏性热效应进行了计算流体力学解析,得出了阀芯的温度场分布。袁王博等[8]研究了U形节流槽的滑阀阀芯热变形,为研究阀芯的热变形提供了借鉴。
目前各学者对于滑阀的研究手段已经非常成熟,解决了滑阀工作过程中的许多问题,但是对于具有双U形节流槽滑阀的研究仍然不全面。本研究对双U形节流槽数量分别为2, 3, 4, 5, 6,阀口压差分别为5, 10, 15, 20, 25 MPa时的液压滑阀进行仿真分析,得到液压滑阀在不同双U形节流槽数量、不同阀口压差时流体的速度场,以及滑阀阀芯的温度场与应变场。
1 数值模型的建立
1.1 流体与传热控制方程
液压阀内流体的流动以及流体与固体之间的传热始终遵循3个物理规律,分别是能量守恒、质量守恒以及动量守恒[9]。
能量守恒方程为:
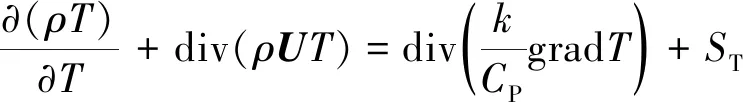
(1)
质量守恒方程为:
(2)
动量守恒方程为:
(3)
式中,ρ—— 流体密度
T—— 流体温度
U—— 速度矢量
k—— 流体传热系数
CP—— 流体的比热容
ST—— 流体黏性耗散项
▽ —— 散度
F—— 作用于流体上的质量力
p—— 流体压力
μ—— 动力黏度
Δ —— 拉普拉斯算子
热流耦合分析问题为温度场的第三类边界条件[10]和热耦合所特有的边界条件。当流体与固体的温度不同时,会发生对流换热,此时固体表面的热流密度与温度差成正比,即:
(4)
式中,n—— 换热表面的外法线
h—— 换热系数
TW—— 边界面温度
Tf—— 流体温度
Ts—— 固体区域温度
在耦合边界还应满足连续性边界条件,即:
TW|f=TW|s
(5)
通过耦合迭代求解热流密度以及耦合面温度,初始条件设置为:
T|t=0=T0
(6)
1.2 仿真模型及边界条件设置
实际工况中应用的滑阀结构比较复杂,为了方便研究计算,省略掉滑阀中多余的零部件,建立其简化模型。此模型主要由进油口、出油口、流体域、阀芯组成。
在Fluent计算过程中,为了保证计算的可行性,需要对流体做以下假设[11]:
(1) 流体为不可压缩的牛顿流体;
(2) 流体为单向流;
(3) 流体为紊流,采用标准的k-ε模型[12]。
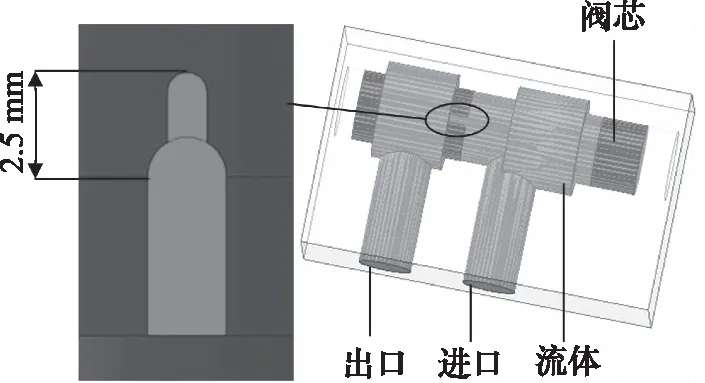
图1 双U形液压滑阀仿真系统模型

图2 双U形节流槽结构图
不同类型的液压油具有不同的牌号,上述模型中,流体材料选用常用的46号液压油,固体材料选用阀芯的常用材料45号钢。流体与固体材料参数如表1、表2所示。

表1 46号液压油材料属性
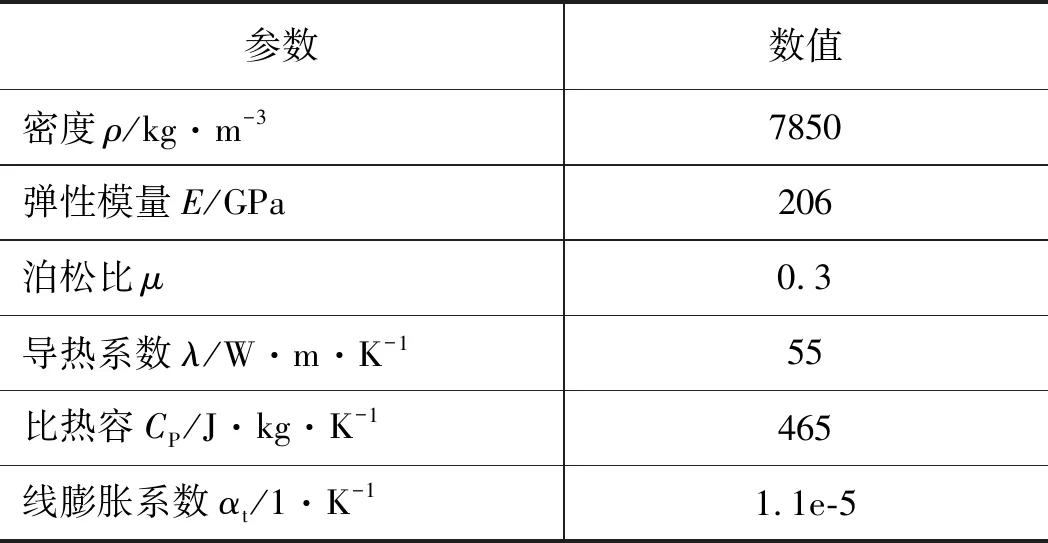
表2 45号钢材料属性
在进行仿真时,忽略阀套对液压阀内部的影响,将流体与阀套接触面设置为绝热边界条件。阀芯两端设置为对流换热条件,阀芯与流场接触面设置为耦合边界条件。假设工作环境温度为室温[12],设置阀芯表面与流体初始温度为300 K,即26.85 ℃。阀芯实际在阀腔中左右移动,在稳态仿真条件下默认阀口开度固定阀芯静止,因此假设阀芯左右端面为固定面。
2 阀腔流场动态特性分析
2.1 阀口压差对流场的影响
当节流槽数量为4,阀口开度为2.5 mm时,分别设置阀口压差为5, 10, 15, 20, 25 MPa,得到了不同阀口压差下流场内速度分布特性,如图3所示。
结果表明,阀腔进口侧速度均衡,高流速区域主要集中在节流槽位置,与实际情况相符,在一定程度上反映了该模型的可信度。此外,阀腔出口侧高速流体速度方向与阀腔出口侧壁面呈一定角度,此角度并不会随压差变化而改变。阀口压差在5~25 MPa内,提取不同压差下流体的最大流速,其拟合曲线为v=0.4528 Δp0.5077,拟合优度R2接近为1,如图4所示。结果表明,流体最大流速随阀口压差增大而增大,与流体力学中薄壁出口流速与阀口压差的关系基本相符。

图3 不同阀口压差下流体速度云图

图4 阀口压差对流体最大流速的影响
2.2 节流槽数量对流场的影响
当阀口压差为15 MPa,阀口开度为2.5 mm时,分别设置节流槽数量N为2, 3, 4, 5, 6,得到了不同节流槽数量下阀腔流场速度分布特性,如图5所示。

图5 不同节流槽数量下流体速度云图
结果表明,双U形节流槽数量对于液压阀内的流场特性影响不大。阀腔出口侧高速流体速度方向与阀腔出口侧壁面所呈角度不会随着节流槽数量的变化而改变。提取不同节流槽数量时流体最高流速,其拟合曲线如图6所示。结果表明节流槽的数量不会影响液
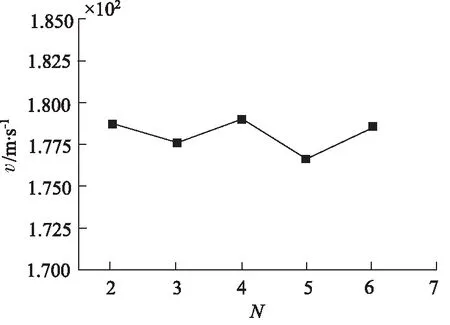
图6 节流槽数量对流体最大流速的影响
压阀内流体的最高流速。
3 阀芯动态特性分析
3.1 阀口压差对阀芯动态特性的影响
1) 阀芯热特性分析
当节流槽数量为4,阀口开度为2.5 mm时,分别设置阀口压差为5, 10, 15, 20, 25 MPa,得到了不同阀口压差下阀芯的温度场,如图7所示。

图7 不同阀口压差下阀芯温度分布云图
结果表明,阀芯的最高温度出现在第一节节流槽顶部与第二节节流槽交界处,这是因为流体流经此处时,在节流槽的节流作用下,致使流体在此处流速急速变大。并且此处流场结构剧烈变化,流体的方向发生改变,此时流体的黏性应力为抵消这种变化而做功,将动能转化为热能。热能聚集在第一节节流槽顶部与第二节节流槽交界处,致使其温度升高。并且一部分热能随流体流出节流槽,在阀芯出口端位置,流体温度高于阀芯温度,因此其发生热传导,导致阀芯出口端局部位置温度升高。提取不同阀口压差下阀芯的最大温升,其拟合曲线如图8所示。结果表明,随着阀口压差的增大,阀芯的最大温升也随之近似线性增大。

图8 阀口压差对阀芯最大温升的影响
2) 阀芯变形分析
当节流槽数量为4,阀口开度为2.5 mm时,分别设置阀口压差为5, 10, 15, 20, 25 MPa,得到了不同阀口压差下阀芯的应变场,如图9所示。
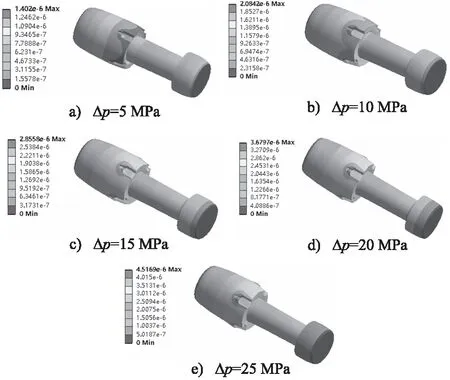
图9 不同阀口压差下阀芯变形量分布云图
结果表明,阀芯的主要变形位置出现在节流槽附近,并且沿着进油口向两边延伸。其最大变形位置始终在第一节U形槽弧顶两端,阀芯温度最高处并不是阀芯最大变形处,这是因为流体对阀芯的冲击也是影响阀芯变形的重要因素。由图9可以得到阀芯在不同阀口压差下的最大变形,其拟合曲线如图10所示。结果表明,随着阀口压差的增大,阀芯的最大变形量近似呈线性增大。
3.2 节流槽数量对阀芯动态特性的影响
1) 阀芯热特性分析
当阀口压差为15 MPa,阀口开度为2.5 mm时,分别设置节流槽数量N为2, 3, 4, 5, 6, 得到了不同节

图10 阀口压差对阀芯最大变形量的影响
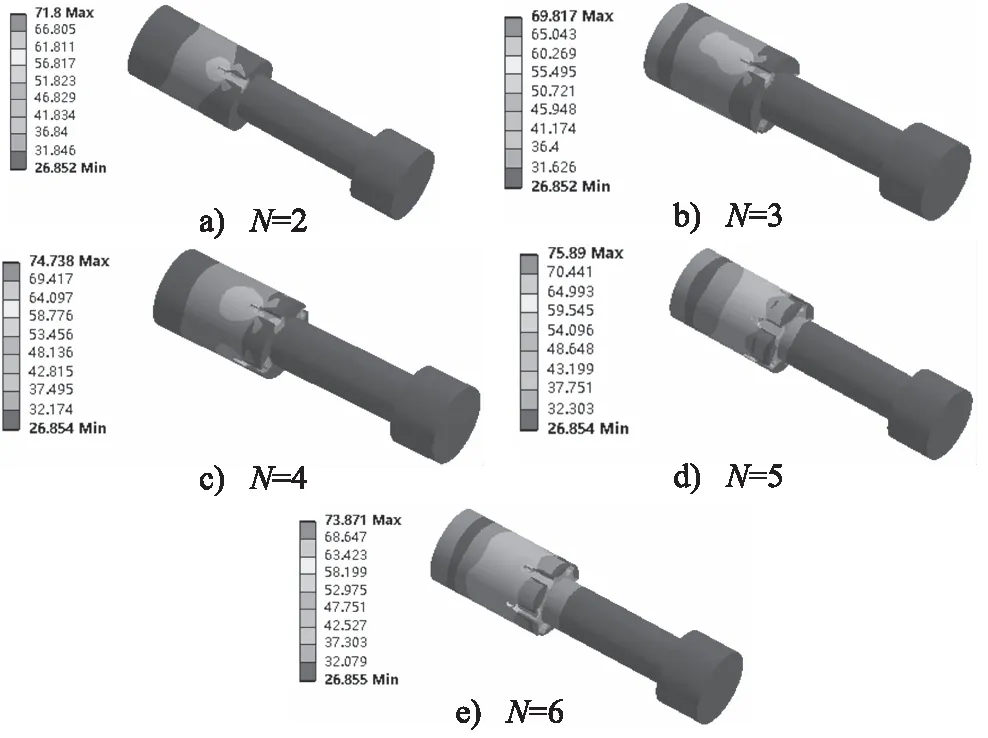
图11 不同节流槽数量下阀芯温度分布云图
流槽数量下阀芯的温度场,如图11所示。
结果表明,节流槽数量对阀芯最高温度的位置没有影响,阀芯最高温度始终在第一节节流槽顶部与第二节节流槽交界处。另外,提取不同节流槽数量时阀芯的最大温升,其拟合曲线如图12所示,结果表明阀芯温度受节流槽数量影响不大。

图12 节流槽数量对阀芯最大温升的影响
2) 阀芯变形分析
当阀口压差为15 MPa,阀口开度为2.5 mm时,分别设置节流槽数量N为2, 3, 4, 5, 6, 得到了不同节

图13 不同节流槽数量下阀芯变形量分布云图
流槽数量下阀芯的应变场,如图13所示。
结果表明,节流槽数量并不会影响阀芯的主要变形位置,其主要变形位置始终在节流槽附近。节流槽数量也并不会改变阀芯的最大变形位置。但在固定阀口压差与阀口开度时,随着节流槽数量的增加,阀芯的最大变形量也在变大。提取不同节流槽数量下阀芯最大变形量,如图14所示。结果表明,阀芯最大变形量与节流槽数量近似呈线性关系。
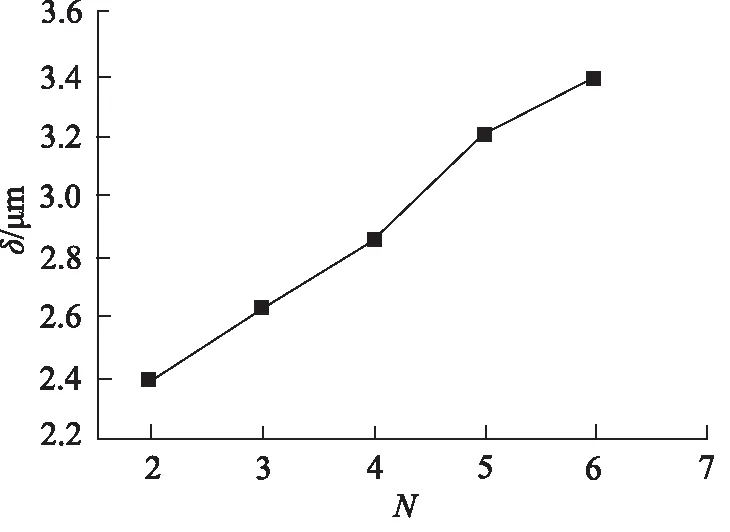
图14 节流槽数量对阀芯最大变形量的影响
4 结论
基于计算流体力学建立了双U形节流槽液压滑阀多场耦合模型,分析了节流槽数量、阀口压差对阀腔内流体速度场、阀芯温度场及阀芯应变场动态特性的影响,通过对比分析,得到以下结论:
(1) 阀芯最高温度始终在第一节节流槽顶部与第二节节流槽交界处;阀芯主要变形位置始终在节流槽附近,并且沿进油口向两边延伸。
(2) 当节流槽数量一定时,随着阀口压差的增加,流体的最大流速变大,阀芯的最高温度和最大变形量近似呈线性增大;阀口压差的变化基本不会影响流体最大流速位置,阀芯最高温度及最大变形位置。
(3) 当保持阀口压差一定时,随着节流槽数量的增加,流体的最大流速以及阀芯的最高温度没有明显变化;节流槽数量对阀芯变形的影响显著,随节流槽数量的增加,阀芯的最大变形量近似呈线性增大。
本研究详细分析了液压滑阀对于不同双U形节流槽数量以及不同阀口压差时流体的速度分布以及阀芯的温度与应变,对于减少滑阀的卡滞现象有重要意义。

