船用起重机主动升沉补偿系统时延的实时控制研究
吴汪洋, 刘贤胜, 郭知峰, 王汉升
(1.海装驻武汉地区第三军事代表室, 湖北 武汉 430000; 2.渤海造船厂集团有限公司, 辽宁 葫芦岛 125000)
引言
具有主动升沉补偿功能的船用液压起重机,在工作过程中存在系统时延和系统非线性所导致的技术参数时变,尤其是系统时延的存在,导致系统的输出信号不能及时反馈给控制器,使控制难度明显加大。国内学者在进行这方面的基础理论研究或者仿真试验时,常常没有把系统时延考虑进去,而实际的船用起重主动升沉补偿系统涉及机、电、液等领域,系统庞大,其机械执行部件间会存在装配间隙, 故忽略系统时延是不符合系统实际的。

图1 主动升沉补偿系统结构组成示意图
当把系统时延考虑进去时,经典PID+Smith预估补偿控制可以解决系统时延引起的控制不稳定问题,但是这必须基于被控对象的模型是精确已知的前提。当被控对象的技术参数发生时变时,Smith预估补偿模型就会与被控对象模型失配,会导致控制器不稳定;而智能广义预测控制对被控对象的模型精度要求不高,尤其是针对存在时延和参数时变的系统,具有良好的自适应控制性能,因此可以很好的将其应用到主动升沉补偿系统时延的稳定控制中。当基于广义预测控制实现了对主动升沉补偿系统时延的稳定控制之后,控制系统的补偿输出总是滞后于起重母船的实际升沉运动一个时延时间,导致升沉补偿系统的实时补偿性能下降甚至失去实时补偿效果。为此,本研究引入极短期预报技术,提前预报出起重母船的升沉运动,解决了控制系统实时补偿输出总是滞后于起重母船升沉运动的问题,实现了升沉补偿控制系统的实时补偿功能,为后续样机产品的研发提供了技术支持。
1 主动升沉补偿系统结构组成
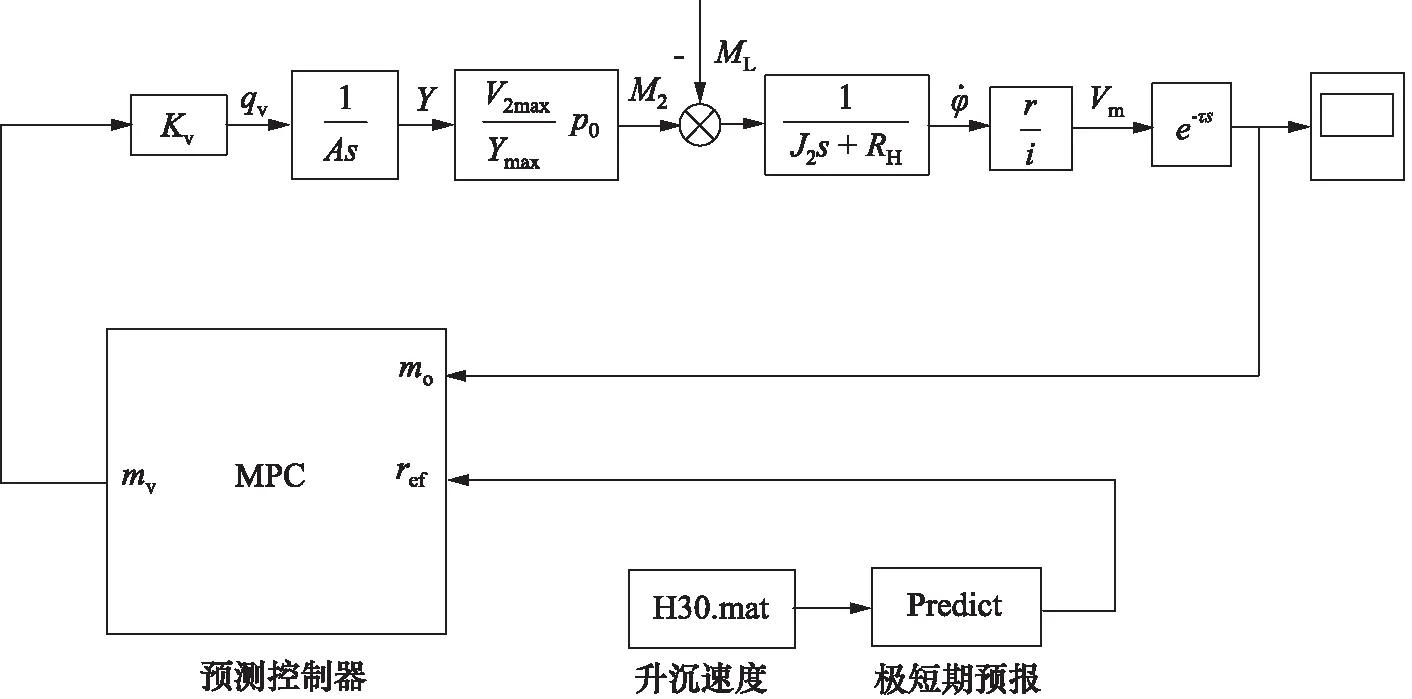
船用起重机主动升沉补偿系统主要由四部分组成:起重母船升沉运动检测系统、控制系统、液压驱动系统、机械执行机构,其结构组成如图1所示[1]。
其具体原理是:当起重船受到风、浪、流的联合作用时,将产生升沉运动,使得起重机无法平稳的对吊载实施下放。开启主动升沉补偿功能后,运动检测系统将实时检测起重母船的升沉运动,然后将检测到的信息传递给控制系统,控制系统根据检测到的起重船运动信息,按照一定的控制算法,发出控制指令给液压驱动系统,然后由其驱动机械执行单元做出与起重母船升沉运动大小相等、方向相反的补偿运动,进而实现吊载的平稳下放。
其中,系统控制算法是整个升沉补偿系统的核心。本研究基于广义预测控制与极短期预报相结合的控制方案进行升沉补偿系统控制算法的设计。
2 主动升沉补偿设备模型建立
2.1 基本假定
采用二次调节单元作为液压驱动装置,执行机构采用减速器内藏式绞车。主动升沉补偿系统机构组成较为复杂,为便于建立其数学模型,作如下合理假定[2-4]:
(1) 传感器、放大器对建模影响忽略不计;
(2) 液压油管、油箱对控制模型的影响忽略;
(3) 机械执行机构摩擦阻力忽略;
(4) 钢丝绳伸缩形变忽略。
2.2 液压驱动单元建模
液压二次调节静液驱动系统,不同于传统的液压传动系统,是一种压力耦合系统,可实现能量的回收再利用,达到节能效果,如图2所示[4]。

1.液压马达/泵 2.变量液压缸 3.电液伺服阀 4.恒压变量泵 5.蓄能器及控制器图2 液压二次调节单元组成结构图
恒压变量泵与蓄能器组成的恒压油源视为理想工作状态,可稳定的向二次元件提供恒定油压。
电液伺服阀自身固有频率远大于补偿系统固有频率,其传递函数可用比例环节来表示:
(1)
式中,Qv—— 伺服阀输出流量
I—— 伺服阀输入电流
Kv—— 伺服阀流量增益
变量液压缸连续方程:
(2)
式中,qv—— 变量液压缸流量
A—— 变量液压缸有效作用面积
Y—— 液压缸内部活塞位移
Ctc—— 液压缸泄漏系数
pL—— 液压缸两腔压差
Vt—— 液压缸两腔总容积
βv—— 液压油体积弹性模量
变量液压缸力平衡方程:
ApL=(ms2+Bcs+KI)Y+FSE
(3)
式中,m—— 液压缸活塞质量
Bc—— 液压缸阻尼系数
KI—— 液压缸等效弹簧刚度
FSE—— 变量液压缸活塞杆与二次元件排量调节斜盘之间的作用力
马达/泵排量调节斜盘受力方程:
(4)
式中,Js—— 斜盘的转动惯量
Ls—— 斜盘转动中心轴至活塞杆根部的距离
Bs—— 斜盘转动时的阻尼系数
Ks—— 斜盘转动时的相当弹性系数
液压马达/泵排量方程:
(5)
式中,V2—— 液压马达/泵排量
V2 max—— 液压马达/泵最大排量
αmax—— 斜盘的最大摆动角度
α—— 斜盘的摆动角度
Ymax—— 液压缸活塞最大位移
液压马达/泵力矩平衡方程:
(6)
式中,M2—— 液压马达/泵转矩
p0—— 恒压网络压力
J2—— 液压马达/泵转动惯量
φ—— 液压马达/泵转角
RH—— 液压马达/泵阻尼系数
ML—— 负载转矩
2.3 机械执行单元建模
本研究选用行星齿轮减速器内藏式绞车作为补偿系统最终执行机构,使减速器与绞车合为一体,减小了安装空间。
行星轮绞车在补偿系统中可看做比例环节,
(7)
式中,r—— 卷筒半径
i—— 减速比
2.4 整体运行数学模型
在满足工程应用的前提下,对设备整体模型进行如下合理简化:FSE是一个小量,不计其作用;把液压缸环节视为一个比例积分环节。设系统的时滞时间为τ,则根据2.2节、2.3节内容,对系统模型进行合理简化,升沉补偿系统整体控制数学模型如图3所示。
3 主动升沉补偿控制系统设计
本研究基于智能广义预测控制进行系统控制算法的设计[5-8]。
3.1 广义预测控制算法
1) 预测模型
广义预测控制采用CARIMA模型作为预测模型:
(8)

图3 主动升沉补偿整体控制数学模型
式中:
A(z-1)=1+a1z-1+a2z-2+…+anaz-na;
B(z-1)=b0+b1z-1+…+bnbz-nb;
其中,Δ=1-z-1表示积分因子;ξ(k)表示白噪声;
2) 预测输出
为了预测超前j步系统输出,引入Dioaphantine方程:
1=Ej(z-1)A(z-1)Δ+z-jFj(z-1)
(9)

(10)
式中:
Gj(z-1)=g0+g1z-1+…+gj-1z-j+1;
其中,j=1,…,N1,N1为预测长度;Ej(z-1),Fj(z-1),Gj(z-1),Hj(z-1)是由模型参数A(z-1),B(z-1)和预测长度j所唯一确定的多项式。则k+j时刻,y(k+j|k)的最优预测值可表示为:
y(k+j|k)=Gj(z-1)Δu(k+j-1)+
Fj(z-1)y(k)+HjΔu(k-1)
(11)
用向量的形式表示为:
Y=GΔU+Fy(k)+HΔu(k-1)
(12)
其中:Y=[y(k+1|k), …,y(t+N1|k)]T;
ΔU=[Δu(k), …, Δu(t+Nu-1)]T(Nu表示控制长度);
E=[E1ξ(k+1),…,EN1ξ(t+N1)]T;
F=[F1,…,FN1]T;H=[H1, …,HN1]T;
采取递推方式求解Ej(z-1),Fj(z-1),Gj(z-1),Hj(z-1),求解Ej(z-1)和Fj(z-1)系数的递推公式:
(13)
求解Gj(z-1)和Hj(z-1)的系数的递推公式:
(14)
递推求解式子(13)、式(14)所需的初始值为:
(15)
根据以上公式,可以求出超前j步系统输出的预测值。
3) 参考轨迹和目标函数
设超前N步预测的参考轨迹的矩阵形式为:
W=[w(k+1),w(k+2),…,w(k+N)]T
(16)
取:
w(k+j)=ajy(k)+(1-aj)yr
(17)
式中,a—— 柔化系数,0 y(k) —— 系统实测输出值 yr—— 系统的给定值 目标函数J为: (18) 写成向量的形式: J=(Y-W)T(Y-W)+λΔUTΔU (19) 4) 最优控制律的求解及滚动优化 对J求偏导数,得到使J取最小值的控制律: ΔU=(GTG+λI)-1GT[W-Fy(k)-HΔu(k-1)] (20) 在实际应用中,采取滚动优化的原则,每次仅将第一个分量加入系统,即: u(k)=u(k-1)+Δu(k) (21) 对系统施加了当前时刻的控制量u(k)后,再重复上述步骤,进行下一刻的控制量计算。 5) 反馈校正 在这里,采取广义反馈校正,即利用递推形式的最小二乘法对系统参数A(z-1)、B(z-1)实行时刻的在线辨识、纠正。 采取广义预测控制虽然解决了补偿系统闭环反馈控制的稳定性问题,但因时滞环节e-τs以及广义预测控制算法的影响,使补偿系统的输出补偿量在时间上延时了τ,导致控制系统补偿输出与母船升沉运动不同步,达不到实时补偿效果,如图4所示,引入极短期预报可解决这一问题。 图4 补偿响应输出滞后示意图 极短期预报方法有多种,本研究采用基于自回归AR模型的时间序列法[9-12],应用递推最小二乘法估计模型参数,AIC准则确定模型阶数。 1) 基于AR模型的极短期预报原理 对于AR(p)模型,其一般形式为: x(k)=a1x(k-1)+a2x(k-2)+…+ apx(k-p)+ξ(k) (22) 式中, {x(k),k=1,2,…,N}—— 测量到的已知的时间序列,经处理后可以看作零均值的平稳随机序列 N—— 测量的数据数目 {aj,j=1,2,…,p} —— 模型的系数 p—— 模型的阶数 {ξ(k),k=1,2,…,N} —— 测量误差序列,通常假定其为零均值、方差为δ2的白噪声序列。 令式(22)中的k=p+1,p+2,…,N,(N≥2p), 则有: (23) 定义: X=[x(p+1)x(p+2)…x(N)]T (24) (25) a=[a1a2…ap]T (26) ξ=[ξ(p+1)ξ(p+2) …ξ(N)]T (27) 将式(22)写成向量形式: X=Φa+ξ (28) (29) 考虑到补偿系统的实时性,另一方面为了减少计算机的内存,提高计算速度,对上式进行整理,可以得到其递推形式的最小二乘法估计公式。 (30) 式中,I为单位矩阵。 整理得到其递推形式的参数估计公式: (31) 3) 确定模型阶数的P 模型最优阶数P通过AIC准则来确定。定义Sp(N),I(P): (32) I(P)=log(Sp(N)/N)+2P/N (33) 式中,Sp(N) —— 预测模型残差 I(P) ——P阶预报模型AIC函数值 在预报的过程中,首先设置AR模型的最大阶次M,然后分别令P=1,2,…,M,根据上式求出P取不同值时的AIC函数值I(1),I(2),…,I(M),然后再对其进行比较,求出使P=min{I(1),I(2),…,I(M)}时对应的阶数P,作为估计模型对应的最佳阶次。 4) 预报模型 在式(22)中的模型参数已得到最佳估计后,可以得到未来k+l刻的预报值: (34) 综上,极短期预报的具体步骤为: step1:设定最大的估计阶数M,预报步数l; step2:根据实际动态数据的周期特性选取合理的数据窗口长度N; step3:对窗口内的数据进行零均值处理; step4:设定初值: step7:计算l步预报值: 所以,当开启船用起重机主动升沉补偿系统时,数据采集系统预先采集母船的升沉数据作为极短期预报的预测数据源,并实时更新母船升沉运动采集数据库。 图5为极短期预报效果图,预报时间为超前1.0 s。 图5 极短期预报效果图(超前1.0 s) 通过图4、图6控制系统引入极短期预报前、后的升沉补偿响应输出,可知引入极短期预报后,起重机升沉补偿系统的补偿输出与母船升沉运动完全同步,实现了补偿的实时性。 图6 极短期预报后的升沉补偿输出(超前预报2 s) 液压驱动与机械执行机构性能各技术参数见表1。 根据上述选定的各机构性能参数,按照图3所示的补偿系统控制数学模型框图,使用广义预测控制+极短期预报复合控制方法,应用MTALAB/Simulink软件[8]建立主动升沉补偿系统的仿真模型如图7所示。 设补偿系统滞后时间为1.0 s,合理设置预测控制参数,对补偿系统展开仿真试验研究。 利用AQWA软件计算典型起重船在如图示海情下的升沉运动速度,将计算结果进行补偿系统仿真试验研究,补偿效果如图8~图10所示。 图7 主动升沉补偿系统控制仿真模型 表1 液压驱动与执行机构性能参数 定义补偿精度计算公式: (35) 式中,v—— 起重母船升沉速度 本研究提出的广义预测控制预+极短期预报相结 图8 主动升沉补偿效果图 (浪高H=2.0 m,Pc=98%) 图9 主动升沉补偿效果图 (浪高H=3.0 m,Pc=90.8%) 图10 特殊海情下速度补偿试验结果 (Pc=89.8%) 合的复合控制方法,能够有效解决升沉补偿系统时延及参数时变等问题,在要求工作的海况下补偿精度基本保持在90%以上,达到一般主动升沉补偿系统性能指标要求,这为主动升沉补偿系统的控制策略提供了新思路,也为后续原理样机开发奠定相关理论基础。
3.2 极短期预报算法









4 主动升沉补偿控制系统仿真试验

5 结论




