一种柔索驱动超冗余度机器人结构及驱动机构设计

赵东捷，杜兆才，刘李明

（中国航空制造技术研究院，北京 100024）

0 引言

飞机装配的进气道内腔的装配质量直接影响飞机的安全性、疲劳寿命以及稳定性[1]。而复杂狭窄内腔存在环境复杂、狭窄作业空间受限等特点，一般机构的工作空间难以满足要求[2]。

针对新一代战机的进气道等复杂狭窄内腔的检测要求，本研究提出一套蛇形臂机器人检测统，并进行了实验验证，验证了理论推导的正确性。系统由蛇形臂机器人搭载末端检测单元构成。

1 结构设计

针对新一代战机的进气道工作空间狭窄且存在干涉的问题，拟采用大长径比冗余度柔索驱动机器人（后文简称蛇形臂）搭载末端检测单元进入工作空间进行检测。蛇形臂选取虎克铰关节串联组成机器人本体，这种构型具有足够的自由度且足够灵活，符合在狭小工作空间约束下检测工作的需求。针对具体的检测路径需求以及空间干涉的约束，对蛇形臂进行机构设计，使其可达工作空间能够覆盖检测路径。控制方面设计阵列式高精度柔索驱动结构，节约空间的同时对机器人本体进行高效驱动[3]。

1.1 大长径比冗余度柔索驱动机器人机械结构设计

选取虎克铰关节串联组成柔索机器人本体构型，采用柔索驱动作为机器人的驱动形式。采用全驱动的模式提高稳定性和定位精度，最终形成用于狭小空间作业的大长径比冗余度柔索驱动机器人[4]。

蛇形臂由6 节段组成，节与节之间采用虎克铰串联，每节采用3 根钢丝绳控制，总长度1293 mm（不算末端视觉单元），每节长210 mm，每节外圆直径为60 mm。整体结构如图1 所示。

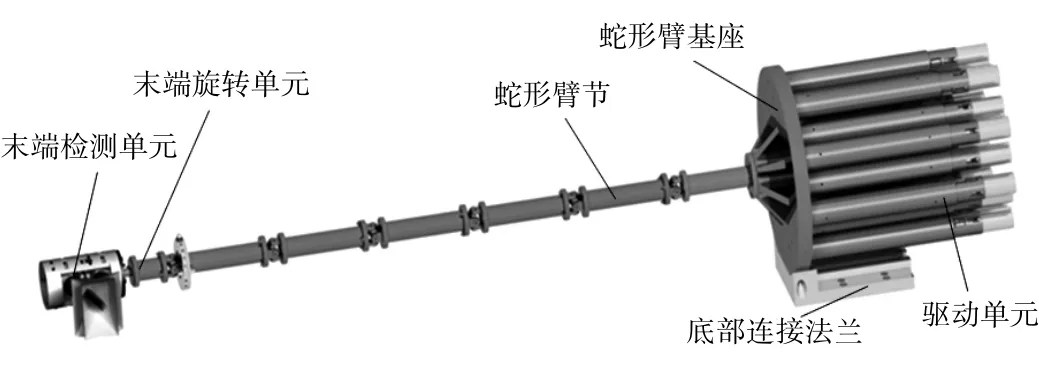
图1 蛇形臂整体结构

各单元具体设计：

驱动单元：驱动单元包括驱动器和钢丝绳两部分，钢丝绳连接在本体单元上，如图2 所示，主要用于控制本体单元运动。本体单元之间通过虎克铰连接。

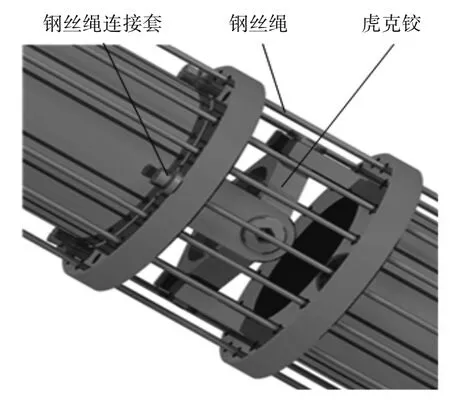
图2 钢丝绳和虎克铰

驱动器集成安装在底座，分别通过丝杠拉动对应的钢丝绳对每个节进行驱动，每根绳索对应一个电机减速器，总共需要18 个电机减速器。把电机减速器丝杠集成到一起，通过圆筒体外壁导向，由丝杠螺母拉伸钢丝绳控制臂节，具体结构如图3 所示。

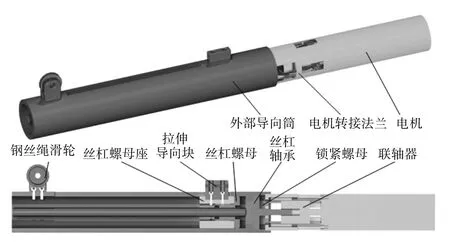
图3 驱动单元

本体单元：蛇形臂的主要组成部分，由蛇形臂节和虎克铰组成，一共6 节，每一节由虎克铰约束，由3根钢丝绳控制臂节，如图4 所示。

图4 本体单元

末端旋转单元：末端旋转单元采用类似蛇形臂节的结构，末端通过虎克铰与前端蛇形臂连接，中间安装电机，电机轴直接与末端检测单元连接，结构如图5 所示。

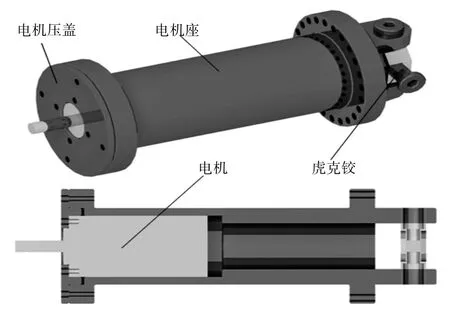
图5 末端旋转单元

1.2 大长径比冗余度柔索驱动机器人驱动方案设计

蛇形臂主要依靠钢丝绳的拉力克服本体重力和末端的重力来驱动，工作场景中蛇形臂的一种典型实际受力情况如图6 所示，以基座中心为坐标原点建立右手坐标系，其中F为末端载荷对蛇形臂末端的作用力，点N为末端载荷重心，点Oi为第i节始端的虎克铰的中心点，H为单个节重心到拉力作用点的水平方向距离，Lj为末端载荷重心到第j节虎克铰的距离，Gi为蛇形臂第i节的重力，点Mi为蛇形臂第i节的重心，Fi为第i节受到的拉力，Lki为蛇形臂第i节重心到第k节虎克铰的距离，为简化计算过程，暂时忽略摩擦力（后期采用安全系数补偿），需满足力矩平衡蛇形臂本体才能保持稳定。以当前姿态下对第一节前面的虎克铰中心点O1的力矩平衡为约束条件进行计算，设第i节的3 根牵引柔索布设位置如图7 所示，点为柔索作用端面转轴中心，点为第i节穿第j个柔索的孔中心，则第i节第j根柔索作用点的坐标值为，其中Ri为穿柔索的孔中心到端面转轴中心的距离为穿柔索的孔中心与端面转轴中心连线与轴的夹角。则表达柔索位置的矢量，设第i节第j根柔索作用力矢量为。根据力矩平衡方程有式（1）。

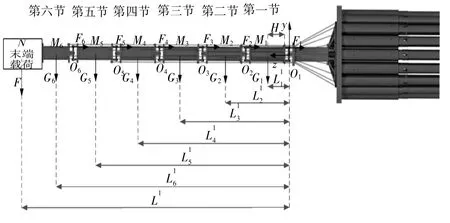
图6 蛇形臂受力情况

图7 第i 节的牵引柔索布置位置

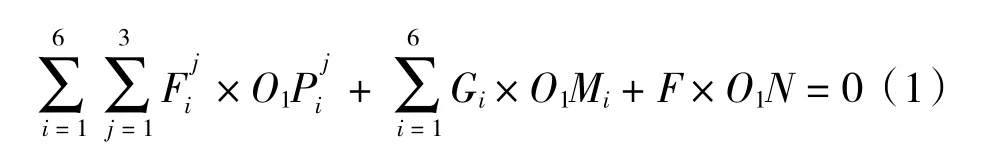
一般地，对第n个虎克铰中心点有力矩平衡方程：

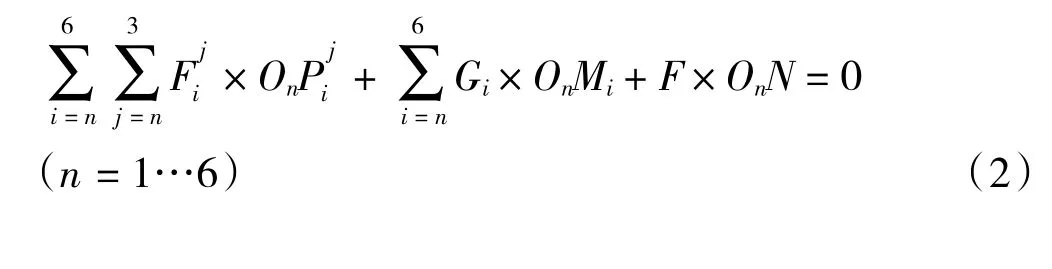
为了方便计算，对各个柔索的位置进行参数化，以虎克铰的十字轴线X轴和Y轴建立坐标系，Y轴与重力反方向，如图8 所示，采用命名对应位置的柔索，a表示不同关节的柔索编号，b表示同一关节的不同柔索编号，采用坐标的方式表示拉力作用的位置，如图8 所示。由于主要克服重力矩，因此，上半平面必须存在驱动点，且理论上钢丝绳越靠近上方所需的驱动力越小。但是考虑到钢丝绳只能提供拉力，如果驱动点均在上半平面，则系统下移完全靠自身重力，没有可控的驱动力，因此，为了保证整体的稳定性，下半平面也设置驱动点，且保证3 个驱动点位于3 个不同象限以提高驱动的稳定性。设置拉力点为图中所示模型外周圆的圆心，选用等边三角形布置方法设置每一节上的拉力点，按照顺时针方向命名各点受力，根据设计模型的实际尺寸给各个钢丝绳拉力点标注位置坐标。

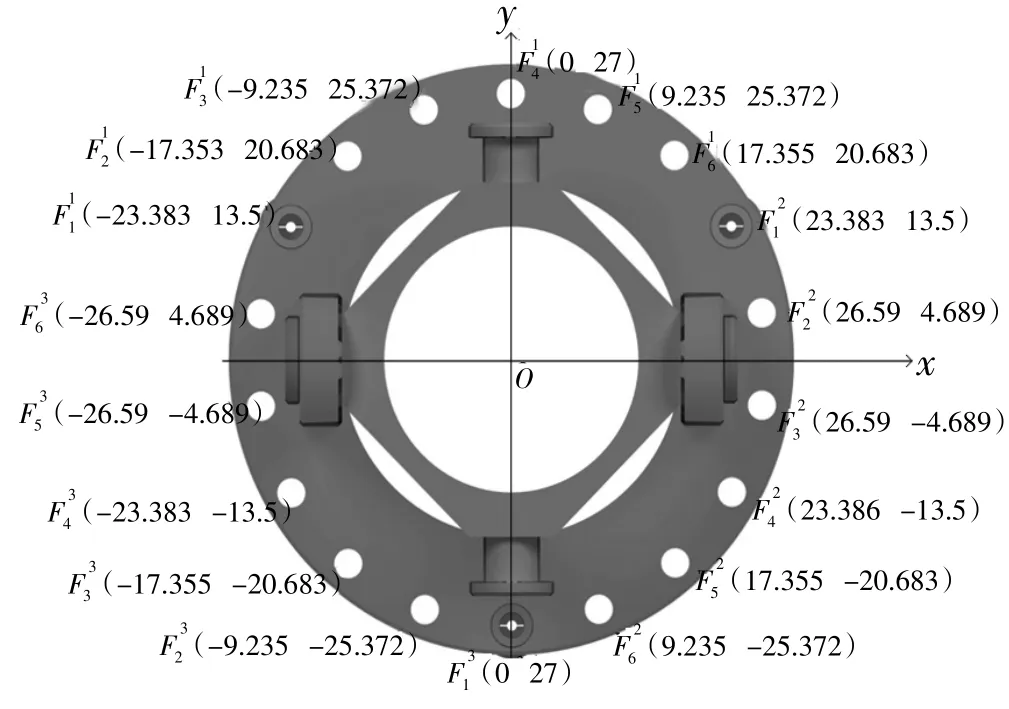
图8 钢丝绳坐标系（坐标值为拉力作用位置坐标）

以单个关节对其前面的虎克铰力矩平衡求解，根据式（2），按照X、Y方向进行正交分解，设单个关节除柔索拉力力矩以外的合力矩为M（M00），以单个关节3 根钢丝绳中的最大拉力取得最小值为约束条件，对每一组受力进行计算：

由对称性原理可得：F5，F6拉力与F3，F2相同，分析上述结果有：

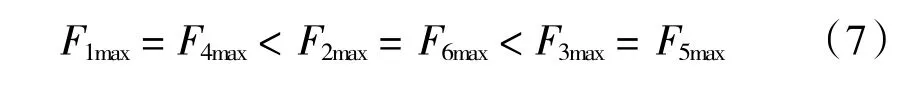
由于越远离基座的关节M值越小，因此，拉力组的最大拉力值越小，应分配在越靠近基座的位置，因此从基座到末端钢丝绳对应的拉力组排序为：F1，F4，F2，F6，F3，F5。

对于当前虎克铰，当其后面的蛇形臂节段呈水平姿态时，阻力具有最大力臂，此时钢丝绳拉力达到最大值（忽略由于转角产生的动力臂的微小变化，后面采用安全系数修正），前文已对蛇形臂水平姿态下第一节的拉力进行计算见式（1），代入各项参数计算得

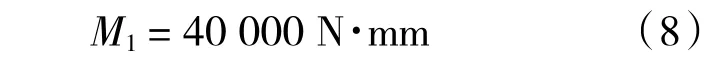
由于第一节采用F1作为拉力组，根据式（4），有

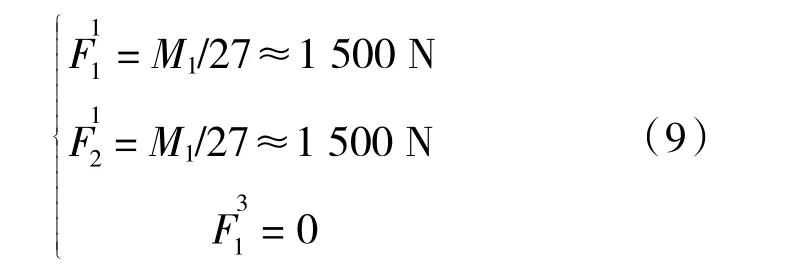
对于蛇形臂第二节，采用F4作为拉力组，F4组中最大拉力和F1组相同，根据式（6），有

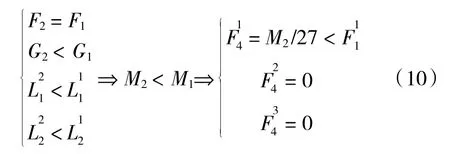
可见第二节所需拉力是小于第一节的。

对于蛇形臂第三节，采用F2作为拉力组，代入实际参数计算，有：

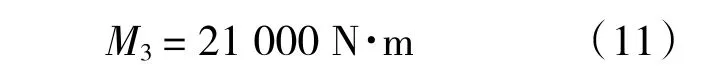
由式（4）计算，有

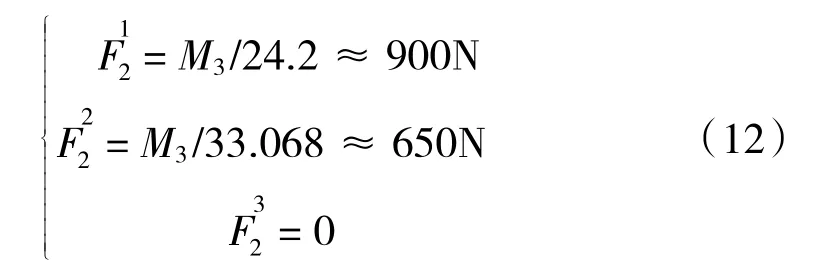
可见，第三节拉力小于第一节，以此推算后续拉力均小于第一节拉力。

以第一节的最大拉力1500 N 来对丝杠选型，同时，计算电机减速器所需参数，制定相应方案。

计算丝杠行程：假设在理想状态下每个关节形成转角为θ，单个关节旋转前和旋转后如图9 所示。

图9 关节状态示意图

由几何关系可得以下等式：

设关节转动了角度θ。由余弦定理可以计算出：绳缆的外弦长为L1，绳缆的内弦长为L2，二者的关系为：

假设每个关节能够同时弯曲，且弯曲角度相同。关节总数为n，则钢丝绳长度的最大差值为：

因此，丝杠行程应为：

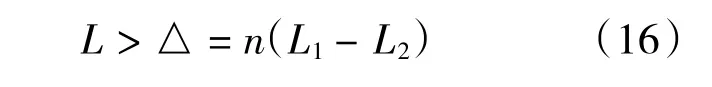
引入实际数据：

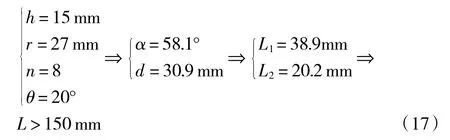
因此滚珠丝杠行程长度为150 mm。

2 实验验证

2.1 机器人检测系统实验设计

本研究主要测试大长径比冗余度柔索驱动蛇形臂的狭小空间运动轨迹，根据轨迹规划软件生成的轨迹控制蛇形臂穿越试验台中的模拟孔，验证轨迹规划能力。具体实验条件见图10、图11。

图10 复杂狭窄内腔装配质量机器人智能检测系统

图11 模拟工作环境试验台

2.2 机器人检测系统轨迹参数计算

根据轨迹理论，采用Matlab Robotics Toolbox 求解。这里选取大长径比冗余度柔索驱动机器人的初始状态和检验状态进行验证。基于5 次多项式轨迹，得到超冗余度机器人运动轨迹（图12），运用雅克比矩阵伪逆求的超冗余度机器人的逆解，再进一步得到各关节角度变化，角速度变化、角加速度变化（图13～图15）。

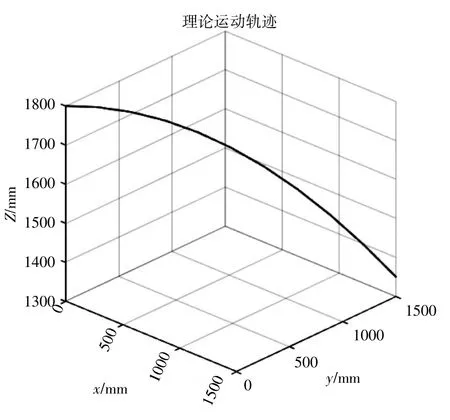
图12 线曲迹轨器行执端末

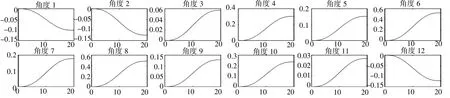
图13 各关节角度变化曲线

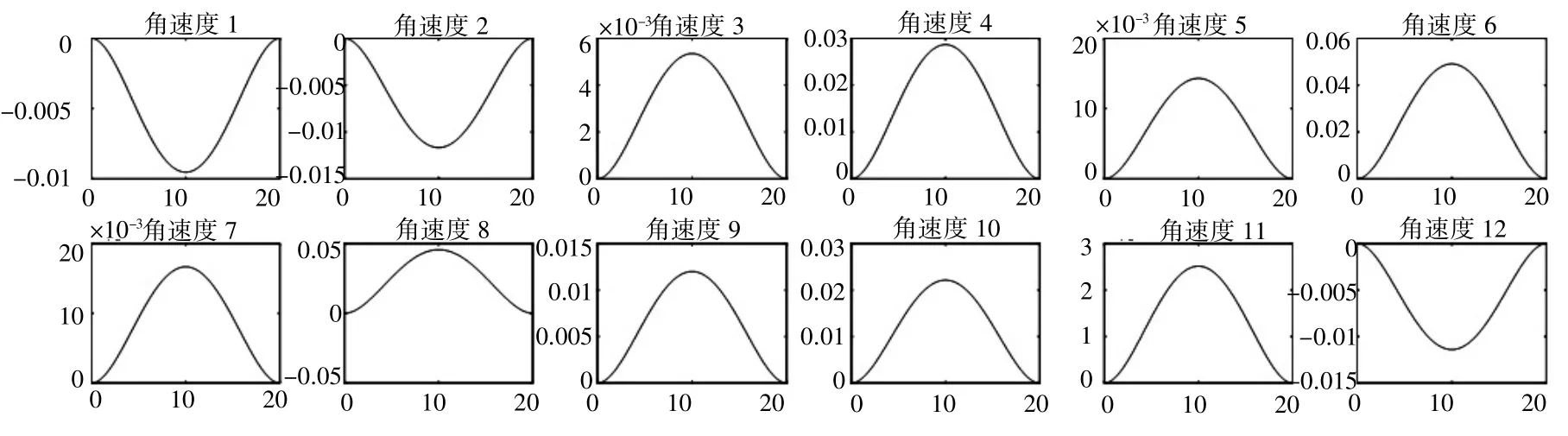
图14 各关节角速度变化曲线

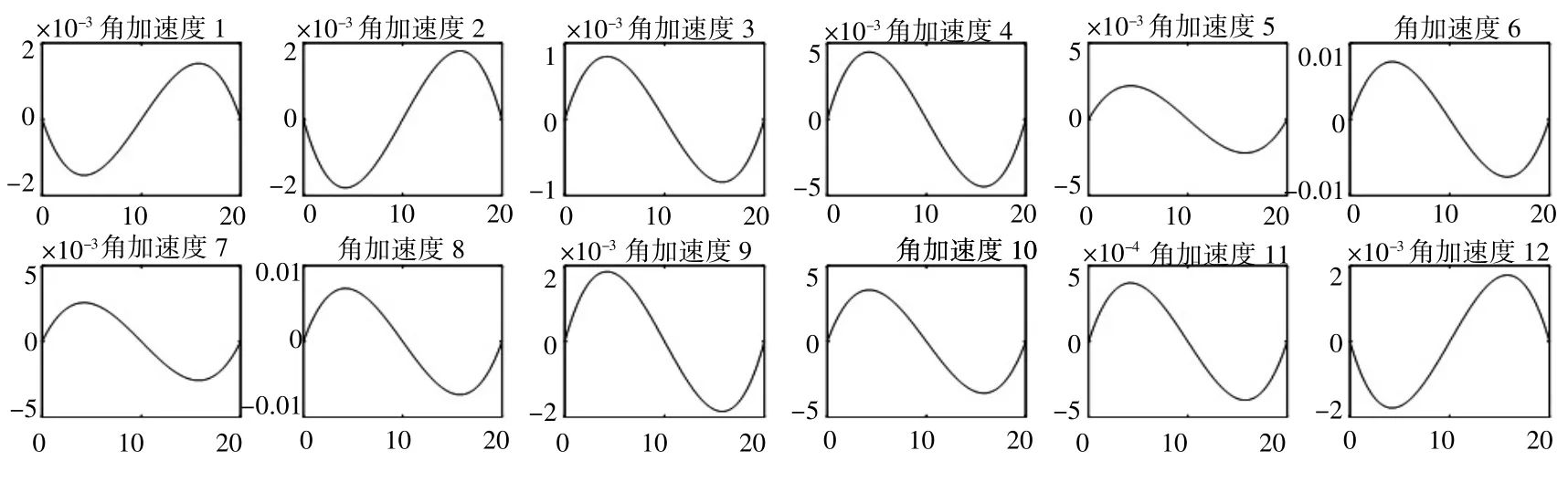
图15 各关节角加速度变化曲线

2.3 机器人检测系统实验结果

采用前文1.2 中的计算的大长径比冗余度柔索驱动机器人轨迹驱动参数对蛇形臂进行驱动，最终运动到如图16 所示，采用激光跟踪仪测量实际运动过程中末端到达的点位，此处采集11 个点，点坐标见表1。通过采集点通过3 次样条插值方法拟合蛇形臂末端在当前驱动参数下的实际运动轨迹，将实际运动轨迹与理论运动轨迹进行对比，分别计算每个实际采集点到理论曲线的最小距离，结果见表1。分析表1 可知，随着运动轨迹的延长，实际轨迹与理论轨迹的偏差越来越大，最大偏差为6.7 mm。采用Matlab 绘制理论轨迹曲线和实际轨迹曲线，如图17 所示，根据图中曲线分析以及表1 中结果可知末端运动路径与理论轨迹曲线基本吻合。此误差将通过激光跟踪仪标定进行修正。

图16 狭窄内腔装配质量机器人智能检测系统测试状态

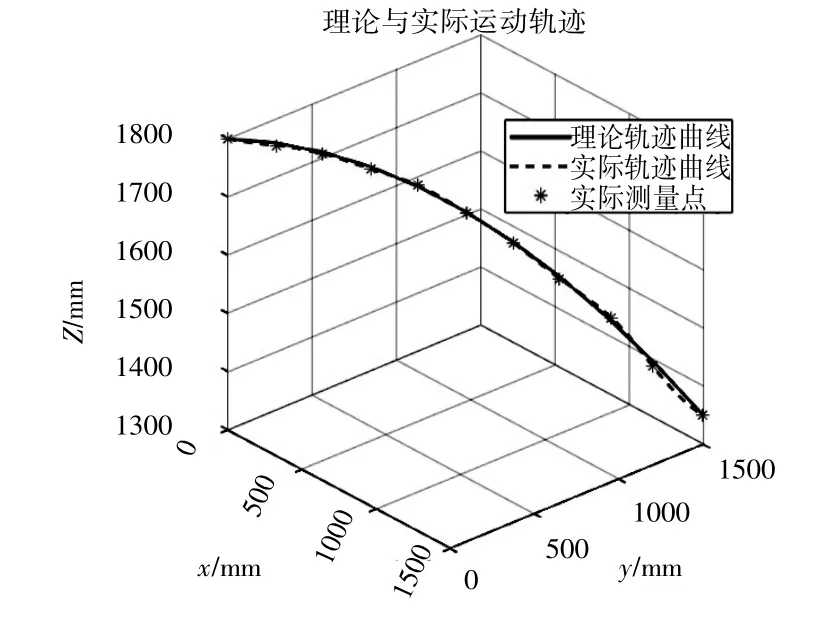
图17 狭窄内腔装配质量机器人理论运动轨迹与实际轨迹对比

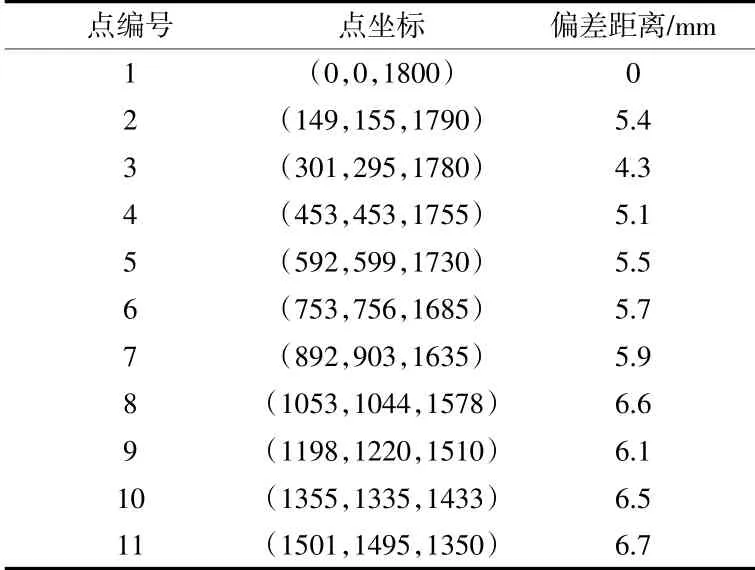
表1 实际点位参数及偏差距离

3 结束语

本研究针对新一代战机的进气道等复杂狭窄内腔工作环境提出了一套蛇形臂机器人检测系统，通过蛇形臂机器人搭载末端检测单元实现在狭小空间的工作，从应用领域来讲，本系统克服了对于狭窄内腔人工难以工作的困难，同时，通过对机器人本体结构和控制算法的优化，提升了机器人的运动精度，进而提升了新一代战机复杂狭窄内腔装配质量检测精度及效率。